Trans. Nonferrous Met. Soc. China 22(2012) s61-s67

Effect of severe plastic deformation on microstructure and mechanical properties of bulk AZ31 magnesium alloy

XU Shu-bo^1, 2, QIN Zhen¹, LIU Ting¹, JING Cai-nian¹, REN Guo-cheng¹

1. School of Materials Science and Engineering, Shandong Jianzhu University, Jinan 250101, China;

2. State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Technology, Wuhan 430074, China

Received 9 July 2012; accepted 20 August 2012

Abstract: The equal channel angular pressing (ECAP) was used to make large plastic deformation of magnesium alloy, and ECAP processing and relevant process parameters were obtained by using finite element method. The strain distributions in the workpieces and the loads on the dies were studied. The mathematical model of accumulated deformation results, microstructure refinement and mechanical properties were established. Through the analysis, the relationships between grain refinement and mechanical properties were obtained. The refined grain size and the obtained mechanical properties are forecasted by using characterization of accumulation deformation.

Key words: magnesium alloy; AZ31 alloy; equal channel angular pressing; process parameter; grain refinement

1 Introduction

Magnesium alloy as a new type of metal material has super high strength, super high stiffness, strong electromagnetic shielding and radiation resistant capability. Ultra-fine grained (UFG) magnesium alloy with equiaxed grain has been widely used in the automotive, electronics, aerospace and defense and other fields. Many countries regard it as important strategic resources in the twenty-first century and put forward some major research and development plans. Under this background, it is important to study the refinement mechanism and production process of the UFG Mg alloy. In order to make magnesium alloy used in the industrial field well, some ways were proposed to improve the mechanical properties of magnesium alloy. Grain refinement and control of the structure is an effective way to improve the performance of metallic materials. The grain refinement can greatly improve the strength, ductility and super plastic forming of magnesium alloy at room temperature. There are many grain refinement methods, such as extrusion, forging, rolling and subsequent recrystallization annealing process. Equal channel angular pressing (ECAP) as a forming processing technology to refine the microstructure, improve properties and material formability of magnesium alloy has been studied widely. The main teams of studying ECAP are Segal¡¯s team at University of Texas in USA, Valiev¡¯s team at UFA Aviation Institute in Russia, Langdon¡¯s team at South California Industry University, Da Yoji¡¯s team at Kyushu University in Japan and so on [1]. In China, Xi¡¯an University of Architecture and Technology, Harbin Institute of Technology, Tsinghua University, and Metal Research Institute of Chinese Academy of Sciences performed ECAP process with experiments and simulations. The ECAP processed magnesium alloy by simulating different process parameters, and understanding and mastering the rules can improve the ECAP processing [2].

2 ECAP principle

The principle of ECAP is illustrated schematically in Fig. 1. Equal channel angular pressing is a shear deformation process that billets are pressed into a special die to achieve a large deformation. Billet from the die channel was forced with extrusion. A shear deformation and a large shear strain have been obtained in the materials, so that the grains can be refined. Grain refinement during the extrusion process is concluded as follows: coarse grains along the shear direction are elongated banded structure, and then form at corned dislocation and dislocation cell. Further with the deformation, dislocation cell number increases, cell size decreases, cell wall has high dislocation density, and a number of small corners of crystal forms. As a result, the large grains are crushed into sub-grains with low angle boundaries and sub-grains have been destroyed, gradually formed equiaxed grains with high angle boundaries. And then, grain orientation difference increases and large corner grain boundaries forms. Finally, grains are refined to submicron or nanometer level. The submicron ultrafine grained microstructures of aluminum [3-6], copper [7-8], magnesium [9-11], titanium [13-14] and other metal or alloys can be prepared by this method.

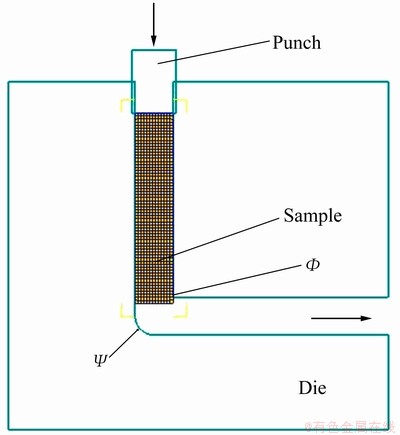
Fig. 1 Schematic diagram of ECAP

3 Simulation analysis

Different process parameters have different effects on the microstructure and properties of magnesium alloy processed by ECAP[15]. In this work, two process parameters, i.e. the die corner and the paths of the extrusion, were analyzed.

3.1 Effect of die corner angle

Figure 2 gives the effective strain contours in the cross-section of workpiece for different corner angles at ¦µ£½90¡ã, and the change of shape and deformation of the ECAP sample in the deformation process by the finite element analysis. The simulation results show that the deformation of each part of the whole sample is not uniform. The front end and back end of the sample are not extruded through the channel angle shear zone. So the front and back of sample have little change. The middle of the sample deformed relatively uniformly through shear area. And the deformation gets more uniform between the surface and the middle area of cross-section, but the strain is small. It can be known that the deformation uniformity of the pressed workpiece for consecutive pressing process is independent of the pressing direction. The effective strain and the deformation get larger with decrease of die corner angle. The deformation of the middle cross-section is more serious than that of the top and bottom cross-section, which produces adverse effect on the deformation uniformity.

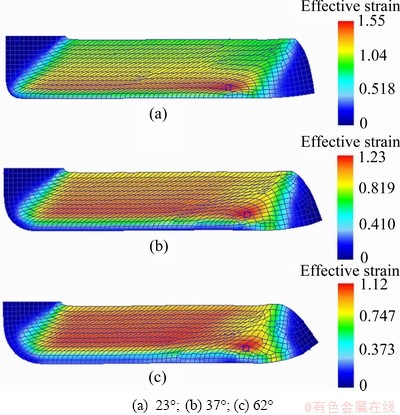
Fig. 2 Grid change of different die corner angles

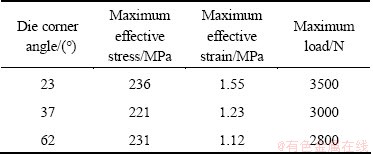
Table 1 gives the relationships of the maximum punch load, maximum effective stress and maximum effective strain with different die channel angles. The maximum effective stresses are 236, 233 and 231 MPa when the die corner angles are 23¡ã, 37¡ã and 62¡ã, respectively. Therefore, through the simulation analysis, it can be indicated that the largest stress drops and the effective stress gradually decreases with the die corner angle increasing. While the effective stress in the corner keeps higher, adjusting the die corner angle has important effect on the die corner effective stress distribution, but the highest effective stress inside corner has little change. So the stress is relatively concentrated in the die corner, and a bigger corner angle should be designed to avoid stress concentration in the die corner. The distribution of the effective strain is similar to effective stress in the extrusion. The maximum effect strains are 1.55 and 1.23 when the die corner angles are 23¡ã and 62¡ã, respectively. The smaller the die corner angle, the larger the effective strain. The effective strain increases gradually from the outside to the inside corner. The die corner angle ¦· gets larger, the total strain of the sample decreases gradually. When the die is designed, not only the accumulation of the deformation, but also the deformation uniformity and reasonable selection of appropriate die corner angle should be considered. The maximum loads of stable stage are about 3500, 2800 and 2700 N when the die corner angles are 23¡ã, 37¡ã and 62¡ã, respectively. It can be indicated that with the increase of die corner angle, the maximum load of the extrusion reduces gradually during the extrusion process.

Table 1 Relationships of maximum punch load, maximum effective stress and maximum effective strain with different die corner angles

Therefore, considering the evolution law of the effective stress of extrusion process, the strain accumulation law of the extrusion of sample and the load change rule, die corner angle must be selected carefully. To obtain better deformation distribution and higher strain of extrusion parts, die corner angle range should be generally equal to or slightly higher than 37¡ã.

3.2 Effect of extrusion passes

The simulation results indicate that reasonable selection of die geometry and process parameters can improve the distribution uniformity of the extrusion deformation and strain accumulation. But the effective strain of single-pass ECAP is small and the accumulative deformation distribution is not uniform. In order to obtain the extrusion with deformation uniformity, extrusion parts need to be accumulated large strain. Therefore, multi-pass pressing helps effective strain to accumulate in the sample strain. Four passes were simulated and the effective stress, effective strain and load curves were analyzed, which can lead into a more rational selection of the pressing pass.

Table 2 gives the relationships of the maximum punch load, maximum effective stress and maximum effective strain for different pressing passes when the die corner is 90¡ã. It can be seen from Table 2 that the extrusion maximum effective stresses are 233, 251, 259 and 288 MPa, respectively, after extrusion for four different passes. Effective strain increases with pressing pass. The load consistently increases with the pass time, but the increase is not obvious. It can be seen that the maximum loads are 3000, 3500, 3550 and 3600 N, respectively.

Table 2 Relationships of maximum punch load, maximum effective stress and maximum effective strain with pressing pass

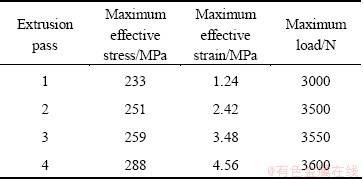
Figure 3 gives the effective strain distribution curves along the height of the cross-section for four passes pressing. The strain distribution of x=35 section extrusion is shown in Fig. 3. The strain distribution of the extrusion after four-pass pressing is not uniform. The trend is first increasing then decreasing from the upper surface to the lower surface. Deformation is mainly concentrated in the central part of the extrusion, the small deformation in the two surfaces. It can be seen from Fig. 3 that the strain of the extrusion accumulates from single-pass pressing to the four-pass pressing and the strain increases gradually. After repeated extrusion, the grain of sample will receive different levels of refinement, and pressing load increases accordingly.

In summary, the sample has optimum properties, i.e. a certain strain can be obtained and the stress is not high at the same time.

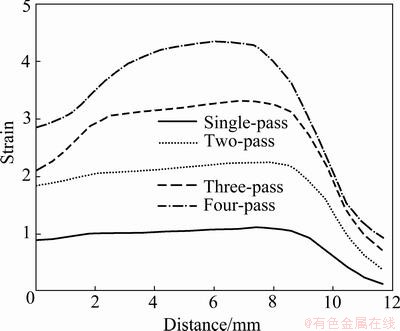
Fig. 3 Effective strain distribution curves along height of cross-section for four passes of pressing of route A

4 Properties of ECAP processed materials

4.1 Microstructure evolution of ECAP processed AZ31 magnesium alloy

The changes of grain grid of AZ31 during the ECAP process were simulated by DEFORM. AZ31 grains can be refined via ECAP deformation. FENG and AI [16] studied the processed AZ31 Mg alloy through ECAP at 673 K, and observed the variation of the microstructure in the material for different passes. The original grain size was 120 ¦Ìm without ECAP, the grain size was down to about 18 ¦Ìm after single-pass, and grains were obviously refined. Grains got further refined with the increase of the number of the extrusion. KIM [17] also measured AZ31 magnesium alloy grain sizes after various passes by ECAP at room temperature. Figure 4 gives the relationship between extrusion pass and grain size at different temperatures. As shown in Fig. 4, at room temperature, the grain size of AZ31 magnesium alloy is 48.3 ¦Ìm before ECAP and 8.1 ¦Ìm by single-pass pressing and can be significantly refined. Crystallite dimension had varying degrees of refinement after two-pass, three-pass and four-pass channel extrusion corresponding to grain size of 6.3 ¦Ìm, 4.3 ¦Ìm and 2.5 ¦Ìm, respectively. Thus AZ31 magnesium alloy grain can be apparently refined. Figure 4 shows that the impact of the temperature on crystallite dimension is very significant. With the increase of temperature, the grain gets coarsening and the grain size can also be refined. Therefore, a lower temperature should be chosen to meet the technological requirements.

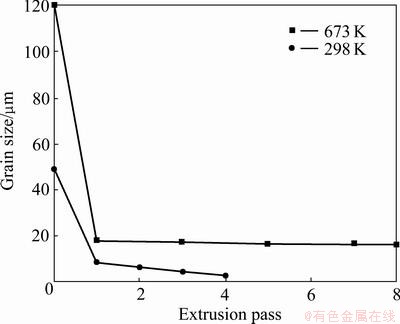
Fig. 4 Relationships between extruded pass and grain size at different temperatures

4.2 Mechanical properties of ECAP processed AZ31 magnesium alloy

4.2.1 Yield strength and tensile strength

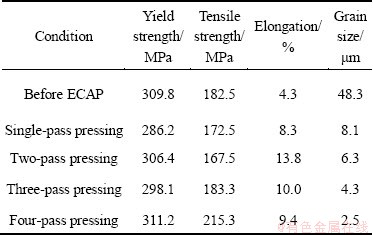
Table 3 gives the grain size and mechanical properties of AZ31 magnesium alloy at room temperature before and after ECAP process. The mechanical properties of AZ31 magnesium alloy by ECAP alters with the changes of the extrusion pass. The material yield strength (YS) is 182.5 MPa before extruded. The yield strengths slightly decrease by 5.47% and 8.22%, respectively, after single-pass and two-pass extrusion. The phenomenon that with the decrease of grain size, the strength declines is not inconsistent with Hall-Petch formula. This is because the grain size and texture have great influence on yield strength. The pole density of texture is small after four-pass pressing during ECAP process. The increase of yield strength is mainly the result of grain refinement. Unlike traditional extrusion, the grain is refined obviously after warm extrusion. Grains in all samples with initial textures parallel gradually to near basal orientation (extrusion direction {0001} plane) through different ways. As the fiber texture of the base plane {0001(-)} is hard orientation, the plastic slips are difficult to occur in the basal plane during tension at room temperature. Therefore, the yield strength of the alloy can be improved. The grain refining and texture strengthening are the reason of that traditional extruded material yield strength is higher than that of the ECAP extruded material. The grains are finer and the texture density also gets larger, and the yield strength and the tensile strength are greatly improved after four-pass ECAP processing. The yield strength and tensile strength can reach 215.3 MPa and 311.2 MPa after processed four-pass pressing, respectively.

Table 3 Grain size and mechanical properties of AZ31 magnesium alloy at room temperature before and after ECAP process

4.2.2 Ductility and toughness

As shown in Fig. 5, the material elongation is 4.3% before extrusion. The elongations of the material increase to 8.3% and 13.8% after single-pass and two-pass pressing, however, the elongations decrease 10.0% and 9.4% after three-pass and four-pass pressing. The result shows that the ECAP can improve the ductility and the toughness of alloy [18].

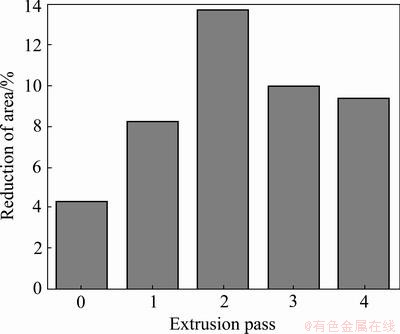
Fig. 5 Reduction of area variation with extrusion pass

4.2.3 Macro-hardness

The macro-hardness of AZ31 magnesium alloy specimen processed by ECAP increases significantly with the increase of the extrusion pass. KIM et al [17] analyzed the influence of different passes on the material mechanical properties by experiment.

The relationship between extrusion times and macro-hardness is shown in Fig. 6. As shown in Fig. 6, the original hardness of workpiece is 43.96 MPa, and the hardness of the material is 63.57 MPa after one time extrusion. With the increase of the pass, the hardness also continues to grow, and reaches the maximum, 90.81 MPa, after three-pass extrusion.

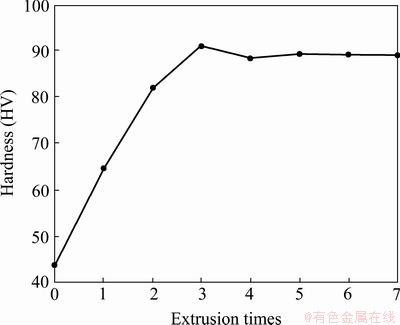
Fig. 6 Relationship between extrusion times and macro- hardness

The hardness of the material through four passes slightly lowers and it is basically consistent in subsequent passes with no significant changes. This is because the dislocation pileup decreases in the grain boundaries, and the dislocation energy reduces with the decrease of grain size. The hardness rises slowly because the grain is basically a tiny isometric crystal via four-pass, with the improvement of deformation coordination between grains, the overall dislocation dynamic lessens, and the softening effect and work hardness brought by dynamic recovery tend toward balance. In subsequent passes, the organizational morphology is basically unchanged. Although the grain size continues to reduce with the deformation, the macro-hardness is essentially the same [19].

4.3 Relationship between grain refinement and mechanical properties

Grain refinement has a significant impact on the performance of the material, according to the Hall-Petch equation, as the grain size is reduced, the hardness and strength of the material increase. Multi-pass ECAP process can cumulative uniform strain in the material, so that the grains can be refined. So, it is necessary to study the relationship between grain refinement, accumulation equivalent strain distribution and uniformity.

On the basis of a large number of experimental and theoretical analysis results, the quantitative relationship between the accumulated equivalent strain and average grain size in the main deformation zone after extrusion was deduced from the Gaussian formula. The grain size and mechanical properties of magnesium alloy with ECAP were forecasted.

For the ultrafine-grained materials whose mean geometric of the material grain size is greater than 100 nm, the effect of its grain size on strength can be described with the Hall-Petch (the Hill-Page) formula as

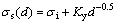                          (1)

where d is the average grain size; ¦Ò_s is the material yield strength, and it is usually replaced by the micro-hardness; ¦Ò_i is the stress required for the grains dislocation motion; K_y is the material constants. The new method that can get the mechanical properties of deformation materials corresponding to average equivalent strain in the main deformation area can be drawn with the Gaussian formula:

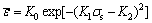                    (2)

where  is the equivalent strain of the workpiece; K₀ is the key strain when the deformation material reaches a certain strength and educability; K₁ is the correction factor (¡Ê(0, 1), and when the material reaches a certain state; K₀ and K₂ are two parameters independent of the critical strain and mechanical properties. Therefore, taking the formula (1) into the formula (2) can create a new method which has a characterization of ECAP accumulated equivalent strain and grain refinement:

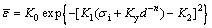           (3)

The yield strengths through different passes were plotted as the images. The relationship of grain size and yield strength of AZ31 magnesium alloy material after deformation is shown in Fig. 7. This calculated result is in line with the Hall-Petch equation, so the yield strength and the grain size is fulfilled linear relationship as follows: ¦Ò_s=¦Ò_i+K_y¡Ád^-0.5 (¦Ò_i=85.2, K_y=6.49). The strain relations inside AZ31 magnesium alloy with ECAP deformation were simulated using two kinds of paths route A and route C. Taking K₀=4.6, K₁=0.049, K₂=10, ¦Ò_i=85.2, K_y=6.49 into formula (3) [20], the equivalent strain of AZ31 magnesium alloy is as follows:

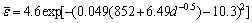     (4)

So it can be gained the relation of the grain size and material internal strain after four-pass pressing. The cumulative strains of path A and path C after extruded four-pass pressing are 4.66 and 4.29. The grain size is 2.5 ¦Ìm in the experiment after four-pass pressing. Taking the grain size into the formula (4), =4.59 is drawn, which is consistent with results of simulation analysis. Therefore, this formula can be applied to the AZ31 magnesium alloy.

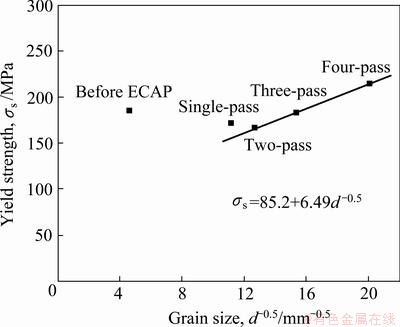
Fig. 7 Relationship between AZ31 magnesium alloy yield strength and grain size

5 Conclusions

1) The metal deformation behavior, strain field, strain uniformity distribution in the workpiece for the different processing routes are presented. Through four extruded, AZ31 magnesium alloy grain is not only been refined, but also the material hardness, strength and elongation are improved. For the multi-pass pressing, it is necessary to find a better route to get uniform effective strain distribution.

2) The refined grain size and the obtained mechanical properties of the AZ31 magnesium alloy can be forecasted by using characterization of accumulated macro-deformation. And then combining the improved model and microstructure simulation part, it can be obtained that the relation of the material external macroscopic plastic deformation, the internal micro-institutions and the mechanical properties.

3) The relationship between grain refinement and mechanical properties are obtained. It will be able to predict the average grain size and mechanical properties of ultra-fine grained magnesium via strain accumulation. If the above method can be confirmed by a large number of experimental results, it can be widely applied to the predication of the average grain size and mechanical properties of various materials after ECAP organizational structure refinement.

References

[1] SEGAL V M, REZNIKOV V I, DROBYSHEVKIY A E. Plastic working of metals by simple shear [J]. Russian Metallurgy, 1981, 19: 99-104.

[2] ZHAO M, LI J C, JIANG Q. Hall-Petch relationship in nanometer size range [J]. Journal of Alloys and Compounds, 2003, 361: 160-164.

[3] WANG J T, IWAHASHI Y, HORITA Z, FURUKAWA M, NEMOTO M, VALIEV R Z, LANGDON T G. An investigation of microstructural stability in an Al-Mg alloy with submicrometer grain size [J]. Acta Mater, 1996, 44: 2973-2982.

[4] FURUKAWA M, HORITA Z, NEMOTO M, VALIEV R Z, LANGDON T G. Microhardness measurements and the Hall-Petch relationship in an Al-Mg alloy with submicrometer grain size [J]. Acta Mater, 1996, 44: 4619-4629.

[5] WANG J T, FURUKAWA M, HORIT Z, NEMOTO M, VALIEV R Z, LANGDON T G. Enhanced grain growth in an Al-Mg alloy with ultrafine grain size [J]. Mater Sci Eng A, 1996, 216: 41-46.

[6] KAWAZOE M, SHIBATA T, MUKAI T, HIGASHI K. Elevated temperature mechanical properties of A 5056Al-Mg alloy processed by equal-channel-angular-extrusion [J]. Scripta Mater, 1997, 36: 699-705.

[7] LUGO N, LLORCA N, CABRERA J M, HORITA Z. Microstructures and mechanical properties of pure copper deformed severely by equal-channel angular pressing and high pressure torsion [J]. Mater Sci Eng A, 2008, 477: 366-371.

[8] XU C Z, WANG Q J, ZHENG M S, ZHU J W, LI JD, HUANG M Q, JIA Q M, DU Z Z. Microstructure and properties of ultra-fine grain Cu-Cr alloy prepared by equal-channel angular pressing [J]. Mater Sci Eng A, 2007, 459: 303-308.

[9] LOKEN S, SOLBERG J K, MAEHLEN J P, DENYSA RV, LOTOTSKY M V, TARASOV B P, YARTYS V A. Nanostructured Mg-Mm-Ni hydrogen storage alloy: Structure-properties relationship [J]. Journal of Alloys and Compounds, 2007, 446-447: 114-120.

[10] ZHENG M Y, XU S W, WU K, KAMADO S, KOJIMA Y. Superplasticity of Mg-Zn-Y alloy containing quasicrystal phase processed by equal channel angular pressing [J]. Mater Letters, 2007, 61(22): 4406-4408.

[11] MATSUBARA K, MIYAHARA Y, HORITA Z. LANGDON T G. Developing superplasticity in a magnesium alloy through a combination of extrusion and ECAP [J]. Acta Mater, 2003, 51: 3073-3084.

[12] KHMELEVSKAYA I Y, PROKOSHKIN S D, TRUBITSYNA I B, BELOUSOV M N, DEBATING S V, TATYANIN E V, KOROTITSKIY A V, BRAILOVSKI V, STOLYAROV V V, PROKOFIEV E A. Structure and properties of Ti-Ni-based alloys after equal-channel angular pressing and high-pressure torsion [J]. Mater Sci Eng A, 2008, 481-482: 119-122.

[13] STOLYAROV V V, ZHU Y T, ALEXANDROV I V, LOWE T C, VALIEV R Z. Influence of ECAP routes on the microstructure and properties of pure Ti [J]. Mater Sci Eng A, 2001, 299: 59-67.

[14] KIM J, KIM I, SHIN D H. Development of deformation structures in low carbon steel by equal channel angular pressing [J]. Scripta Mater, 2001, 45: 421-426.

[15] XU S B, ZHAO G Q, LUAN Y G, GUAN Y J. Numerical studies on processing routes and deformation mechanism of multi-pass equal channel angular pressing processes [J]. J Mater Proc Tech, 2006, 176: 251-259.

[16] FENG X M, AI T T. Microstructure evolution and mechanical behavior of AZ31 Mg alloy processed by equal-channel angular pressing [J]. Trans Nonferrous Met Soc China, 2009, 19: 293-298.

[17] KIM H K. The grain size dependence of flow stress in an ECAPed AZ31 Mg alloy with a constant texture [J]. Mater Sci Eng A, 20089, 515: 66-70.

[18] DUMOULIN S, ROVEN H J, WERENSKIOLD J C, VALBERG H S. Finite element modeling of equal channel angular pressing: Effect of material properties, friction and die geometry [J]. Mater Sci Eng A, 2005, 410-411: 248-251.

[19] LIU Z Q, FENG X M, ZHANG H. Microstructure and mechanical properties of Mg alloy processed by ECAP [J]. Hot Working Technology, 2011, 11: 28-33.

[20] ZHAO J, ZHANG F C, SUN S H, WANG Z H, ZHAO D L, FU W T. A new method of characterizing equivalent strain for equal channel angular processing [J]. Journal of Central South University of Technology, 2009, 16: 349-353.

¾çÁÒËÜÐÔ±äÐζÔAZ31þºÏ½ðÏÔ΢×éÖ¯ºÍÁ¦Ñ§ÐÔÄܵÄÓ°Ïì

ÐìÊ粨^1, 2, ÇØ Õñ¹, Áõ æù, ¾°²ÆÄê¹, Èιú³É¹

1. ɽ¶«½¨Öþ´óѧ ²ÄÁÏ¿ÆѧÓ빤³ÌѧԺ£¬¼ÃÄÏ 250101£»

2. »ªÖпƼ¼´óѧ ²ÄÁϳÉÐÎÓëÄ£¾ß¼¼Êõ¹ú¼ÒÖصãʵÑéÊÒ£¬Î人 430074

Õª  Òª£ºÍ¨¹ýµÈͨµÀת½Ç¼·Ñ¹¼¼Êõ(ECAP)¶ÔþºÏ½ð½øÐоçÁÒËÜÐÔ±äÐΣ¬Ê¹ÓÃÓÐÏÞÔª·¨ÊµÏÖ¶ÔECAP¼Ó¹¤¹ý³Ì¼°Ïà¹Ø¹¤ÒÕ²ÎÊýµÄÊýֵģÄ⣬·ÖÎö³ÉÐιý³ÌÖеÄÍø¸ñµÄ±ä»¯¡¢Ó¦Á¦Ó¦±ä·Ö²¼¹æÂɼ°Æä¼ÓÔØÔغɹæÂÉ£¬È·¶¨Ö÷Òª¹¤ÒÕ²ÎÊýÓ°Ïì¹æÂÉ¡£Í¨¹ý·ÖÎö£¬µÃ³ö¾§Á£Ï¸»¯³Ì¶ÈÓëÁ¦Ñ§ÐÔÄܵĹØϵ£¬ÎªÃ¾ºÏ½ðµÄ¾§Á£Ï¸»¯·½·¨Ìṩ¸üºÏÀíµÄÀíÂÛÖ¸µ¼ºÍ²Î¿¼ÒÀ¾Ý¡£

¹Ø¼ü´Ê£ºÃ¾ºÏ½ð£»AZ31ºÏ½ð£»µÈͨµÀת½Ç¼·Ñ¹£»¹¤ÒÕ²ÎÊý£»¾§Á£Ï¸»¯

(Edited by ZHAO Jun)

Foundation item: Project (20100471513) supported by the China Postdoctoral Science Foundation; Project (2011-P12) supported by the State Key Laboratory of Materials Processing and Die & Mould Technology Foundation; Project (2011008) supported by the State Engineering Research Center of Metal Near Net Forming Foundation, South China University of Technology; Project (201002035) supported by the Postdoctoral Innovation Fund of Shandong Province Foundation

Corresponding author: XU Shu-bo; Tel: +86-531-66368065; Fax: +86-531-66368065; E-mail: shuboxu@yahoo.cn