节理岩体强度参数的数值模拟及工程应用

刘爱华，董蕾，董陇军

 (中南大学 资源与安全工程学院，湖南 长沙，410083)

摘  要：采用数值模拟方法模拟含不同倾角层理面的岩体在抗拉、抗压试验下的破坏过程，从受力、变形和破坏的角度出发，解释节理岩体的破坏机理。在此基础上选取一种层理结构分布明显的岩样，完成常规力学参数下的实验测试与分析，并对数值模拟结果和实验结果进行比较和相关分析。研究结果表明：随层理面倾角的增大，单轴抗压强度先减小后增大，呈“U”型变化趋势；随层理面倾角的增大，单轴抗拉强度呈递减趋势；数值模拟结果得出单轴抗压强度和抗拉强度的各向异性系数分别为0.72和0.24；数值模拟结果与试验测试数据较吻合，为实际工程中复杂节理岩体强度参数的合理确定提供了一条新的途径。

关键词：节理岩体；强度参数；层理面倾角；数值模拟

中图分类号：TD315         文献标志码：A         文章编号：1672-7207(2011)01-0177-07

Numerical simulation and engineering application of

strength parameters of jointed rock mass

LIU Ai-hua, DONG Lei, DONG Long-jun

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: The failure process of rock mass with beddings of different dip angles in compression and tensile tests was simulated with numerical method, and the failure mechanism of rock mass was discussed through analyzing the deformation and failure. A special type of rock sample with clear bedding structure was selected and a series of laboratory tests in conventional mechanical parameters were performed. Then the correlation between numerical simulation results and experimental results was deduced and analyzed. The results show that the uniaxial compressive strength first decreases and then increases with the increase of bedding angles, showing a U-shaped trend, while the tensile strength decreases with the increase of bedding angles. The anisotropy coefficients of the uniaxial compressive strength and tensile strength of numerical simulation results are 0.72 and 0.24, respectively. The numerical simulation and test results are in good agreement, which provide a new way for reasonable determination of the strength parameters of complex jointed rock mass in practical engineering.

Key words: jointed rock mass; strength parameters; bedding dip angle; numerical simulation

岩体是赋存于一定地质环境中，经受过不同时期、不同规模和不同性质构造运动改造的地质体的一部分。由于岩体结构在漫长的地质过程中会形成不同空间状态的结构面，如节理、层理、断层、破碎带等，从而使岩体力学性质呈现出非常复杂的不连续性、非均质性和强烈的各向异性。Harrison等^[1]将裂隙岩体力学性质归纳为不连续、非均匀、各向异性与非弹性。岩体作为一种地质材料，其力学介质类型、分析模型和力学参数是岩石力学的基本问题，也是解决实际岩石工程问题的难点。岩体中结构面的组合、交切等会导致岩体各向异性^[2]。岩体的各向异性是指岩体物理力学参数在不同方向具有差异的性质，由于引起垂直层理面和平行层理面变形的机制不同，这种差异较明显^[3]。岩体所具有的各向异性与求解时采用的各向同性弹性理论假设不能很好地反映岩体工程的实际情 况^[4-7]。岩体材料的强度特性主要受分布在岩体中各类地质弱面的影响和制约，其中节理、裂隙在外载荷的作用下发生、发展与变形破坏直接影响岩体材料的力学强度、力学响应特征及渗透水等力学性质。在以往的研究分析中，节理岩体通常被描述为一种厚度趋于零的单元^[8-10]，如何有效模拟和分析节理岩体的力学特性，深入探讨岩石弱面与岩体各向异性力学与水力学性质之间的内在联系和相关规律，对于岩体工程的设计和施工具有十分重要的理论和工程意义。本文作者基于结构面的倾角变化，应用有限元分析软件ANSYS生成二维有限元模型，分别对包含不同结构面倾角下的岩体进行数值模拟，得出了关于层理分布明显的各向异性岩体的力学特征的一般规律。同时，还针对河南某金矿的生产实际需要，在进行采矿引起的矿区山坡稳定性研究过程中，重点开展岩石弱面与各向异性岩体的力学性质实验研究，获得较可靠的力学参数^[11]，验证了上述数值模拟结果，为不稳定滑坡体形成机理及变形运动规律研究提供了计算依据，并为具体的工程设计提供了合理的计算参数。

1  数值模型的建立及模拟结果分析

1.1  数值分析原理

数值模型中非裂隙部分的岩石类材料利用损伤塑性模型进行模拟，该模型认为材料的基本破坏形式主要分为拉破坏和压破坏，剪切破坏是拉、压破坏的组合形式^[12-14]。材料单轴受拉或单轴受压时，在应力达到抗拉或初始受压屈服强度前，材料中还没有出现塑性变形，应力-应变关系为线弹性的，拉、压受力条件下的应力–应变关系为：

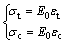                   (1)

式中：E­₀为材料初始弹性模量，即损伤量为0时的弹性模量；ε_t为拉应变；ε_c为压应变；σ_t为拉应力；σ_c为压应力。应力超过抗拉强度或初始受压屈服强度后，材料中的塑性变形逐渐增大，损伤不断积累，应力-应变曲线表现出非线性特性，可将其表达为损伤变量的函数。损伤时的应力-应变关系为：

          (2)

式中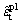：为塑性拉应变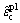；为塑性压应变；d_t为受拉损伤变量；d_c为受压损伤变量。

岩土材料受到外界荷载作用后，随着荷载的增 加，结构的应力状态由弹性过渡到塑性的过程为屈  服^[15-16]。由弹性应力向塑性应力过渡的临界应力状态组成的应力空间称为屈服面，用屈服函数F表示，在屈服面上的应力满足：

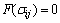                (3)

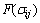＜0表示结构处于弹性状态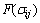；＞0表示结构处于塑性状态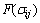；=0表示结构处于屈服临界状态。

大型有限元程序ANSYS为岩体材料由线性进入非线性阶段提供的塑性判据德鲁克-普拉格(Drucker-Prager)塑性屈服准则。Drucker-Prager屈服准则在应力空间中为圆锥面，是Mises准则的推广:

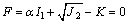           (4)

式中：；

；

；

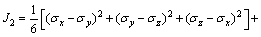
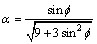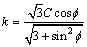
当F≥0时，单元屈服，进入塑性状态；当F≤0时，单元仍处于弹性状态。

1.2  数值模型及参数选取

利用ANSYS有限元计算程序,建立计算模型。本次模型采用静力平面应变下的非线性分析。有限元模型分别取底面直径50 mm、高为100 mm和直径为50 mm、高为50 mm的圆柱状岩体的纵剖面进行抗压和抗拉试验研究, 层理面处于岩体中央，分别建立包含一定的α方向的单一层理面的岩体模型(α为层理面与岩体端面间的夹角)。α取值分别为0°，30°，45°，60°和90°。岩体的泊松比μ=0.25，内摩擦角φ=35°，黏聚力C=0.6 MPa。约束模型底端的自由度，对其上端施加均布线荷载，采用分级加载的增量计算模型模拟其实际加载路径。

单元选择二维结构实体单元PLANE42，这种单元由4个节点定义，每个结点有2个自由度：节点坐标系X和Y方向的平动。该单元具有塑性功能，可用于模拟岩体。岩体本构模型选取Drucker-Prager准则。

材料非线性的计算往往离不开迭代计算，即使是在每步增量荷载作用下的计算也要迭代很多次，收敛时结果存在误差，可能导致进入非线性区的应力状态偏离屈服(破坏)面，即F≠0。此时，应当对应力结果进行修正，使其应力状态落在屈服(破坏)面上，以保证全过程的本构关系仿真。为了减少迭代次数，此处采用修正的Newton-Raphson法求解。

其收敛准则是以各节点处力的不平衡量的范数(即各节点处各项力矢量的平方和的平方根)是否等于各节点(等效)加载力的范数的10^-3，10^-3也称为容差。

本次模型采用的参数由对糜棱岩取样(层理面与试件端面间的夹角分别为0°，58°和90°时)进行实验室测试所得参数提供^[11]。根据试验中α为0°，58°和90°时的弹性模量参数，利用拉格朗日插值法分别得到α为0°，30°，45°，60°和90°时的弹性模量。

1.3  讨论

根据岩石材料在单轴压拉条件下的力学特性可知，在受力达到极限强度以前，随着应力的增大，应变也随之增大。在超过材料的极限强度后，岩体材料发生宏观破坏，由弹性转变到塑性阶段，此时，尽管所受应力逐渐减小，但应变仍呈增大趋势。图1所示为含层理面倾角为0°的模型在受均布线荷载时的应力和相应的应变分布情况，可从其中得出模型在单轴压缩条件下的临界屈服线荷载。倾角为0°时模型单轴抗拉分析图见图2。同理，可从图2中得出层理面倾角为0°时单轴拉伸的临界屈服线荷载。需要指出的是：利用数值模拟方法进行抗压试验时，采用的是直接在模型端部施加载荷的方法。而在实际试验中，直接拉伸试验较难实现，往往采用间接拉伸试验(如劈裂法等)来测定岩石的抗拉强度。

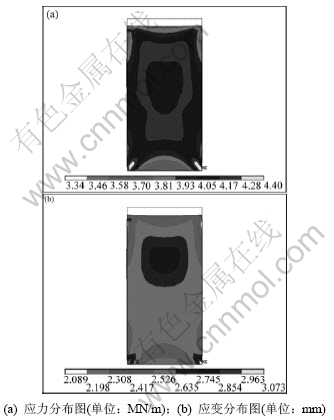
图1  倾角为0°的模型单轴抗压分析图

Fig.1  Uniaxial compression analysis of model with 0° angle

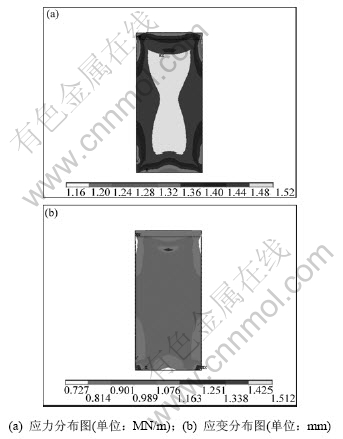
图2  倾角为0°的模型单轴抗拉分析图

Fig.2  Uniaxial tensile analysis of model with 0° angle

通过模型破坏时的屈服线荷载P_l与加载的边长L可以求得模型的单轴试验强度：

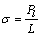                 (5)

试验结果见表1。从表1可见：

(1) 当α=0°时，单轴抗压强度出现最大值(56.0 MPa)；当α为0°~60°时，抗压强度随α的增加而减小；在α为60°~90°时，抗压强度随α的增大而增大。当α=90°时的抗压强度为40.3 MPa。可见：抗压强度随α的增加，其变化趋势为先减小，后增大。

表1  数值模拟实验结果

Table 1  Results of numerical simulation

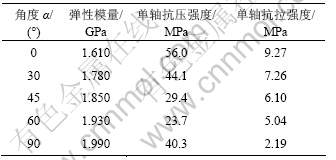
 (2) 抗拉强度随α的变化趋势为：随着α角的增大，抗拉强度呈减小趋势；当α=0°(此时拉应力作用线方向与层理面一致)时，其抗拉强度最大(9.27 MPa)；当α=90° (此时拉应力作用线方向与层理面垂直)时，其抗拉强度最小(2.19 MPa)。

(3) 试件强度随层理面倾角变化体现了节理岩体的各向异性特性。这里用各向异性系数n_aH来衡量岩体的强度随层理面倾角的变化程度：

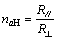                 (6)

式中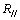：为载荷平行层理时的强度；为载荷垂直层理时的强度。

由表1中数据可以得到单轴抗压强度的各向异性系数为0.72(即40.3 MPa/56.0 MPa)，单轴抗拉强度的各向异性系数为0.24(即2.19 MPa/9.27 MPa)，即垂直于层理方向的抗拉强度近似于平行于层理方向抗拉强度的1/5。由此可见：岩体抗拉强度的各向异性程度比抗压强度的要大。

2  实验验证及工程应用

2.1  实验方法

河南某金矿为全国黄金生产基地小秦岭金矿田北矿带内规模最大的1座金矿。由于长期开采致使矿区地质环境逐渐恶化，自2001年以来，矿区发生过多起采空区塌陷、滑坡、地裂缝等地质灾害。矿区中部的滑坡体对滑坡前缘部位的选厂、设备、建筑、公路及人民财产构成了严重的威胁。糜棱岩为滑坡区域内的主要岩种之一，其层理发育明显，主要分布于断裂带两侧，对断裂带上盘滑坡体的稳定性有较大的影响；因此，测定糜棱岩的力学强度参数，对准确预测滑坡体移动变形规律具有十分重要的意义。

为了研究糜棱岩的力学特征，避免可能影响试件力学性能的其他因素的干扰，从块石样的采集到标准试件的制作都乾地仔细设计。共采集数块具有清晰的细观层理构造的糜棱岩，对每块岩石，按一定的α方向取样。α取值分别为0°，58°和90°(见图3)。将块石分别加工成直径为50 mm、高为100 mm的抗压试件和直径为50 mm、高为50 mm的抗拉试件，根据α取值不同分别制作3组抗压试件和3组抗拉试件。

采用SHT4系列微机控制电液伺服万能试验机对试件进行单轴压缩变形试验和抗拉强度试验，加载过程中，力控速率为200 N/s。

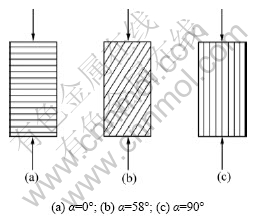
图3  糜棱岩单轴压缩试验示意图

Fig.3  Mylonite samples with different bedding angles for uniaxial compression tests

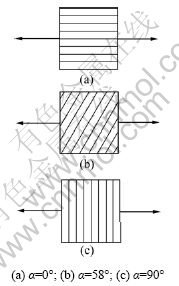
图4  糜棱岩抗拉试验示意图

Fig.4  Mylonite samples with different bedding angles for uniaxial tensile tests

2.2  实验结果分析

2.2.1  单轴压缩变形试验结果分析

通过试样破坏时的最大荷载P与垂直于加载方向的截面积A可以求得试件的单轴抗压强度：

                   (7)

由试验可得到应力与纵向应变关系曲线，而后按下式计算岩石的平均弹性模量：

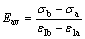                 (8)

式中：E_av为岩石平均弹性模量；σ_a为应力与纵向应变关系曲线上直线段始点的应力；σ_b为应力与纵向应变关系曲线上直线段终点的应力；ε_la为应力为σ_a时的纵向应变；ε_lb为应力为σ_b时的纵向应变。试验结果见   表2。

表2  单轴压缩变形试验结果

Table 2  Results of uniaxial compression tests

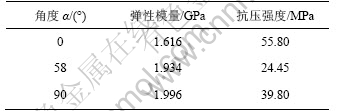
由表2所示数据可以得到糜棱岩的抗压强度随的变化趋势。从表2可见：当=0°时，单轴抗压强度最大；随着的增大，单轴抗压强度呈先减小、后增大的变化趋势。垂直向和水平向的强度有明显差异。

2.2.2  抗拉试验结果分析

采用劈裂拉伸试验法对试件进行抗拉强度试验时，其抗拉强度可通过下式进行计算：

                 (9)

式中：P为试验加载最大荷载；D为试样的直径；h为试样的高度。

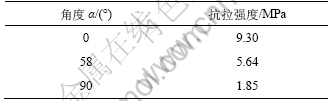
抗拉试验结果见表3。从表3可见：随着的增大，抗拉强度呈送减小趋势；当=0°时，其抗拉强度最大；当=90°时，其抗拉强度最小。垂直于层理方向的抗拉强度约为平行于层理方向抗拉强度的1/5。由此可见：糜棱岩抗拉强度的各向异性程度比抗压强度的要大。

表3  抗拉试验结果

Table 3  Results of uniaxial tensile tests

2.3  破坏模式分析

在试验过程中，当不同时，典型破坏类型见图5。从图5可见：对于糜棱岩，当较小时，常发生横交层理面的破坏；当较大时，常发生沿层理面的破坏。

图5  抗压试验中α=0°和α=90°时的破坏模式

Fig.5  Failure model of mylonite with 0° and 90° in compression test

3  结果分析及工程实例应用

图6所示为数值模拟和试验得出的不同角度层理下的抗压强度变化的对比曲线。由图6可知：数值模拟结果和试验结果较吻合；当=0°时，单轴抗压强度出现最大值；随着层理面倾角的增大，单轴抗压强度先减小，后增大，具有“U”型的变化趋势；在 ＝30°~60°范围内抗压强度达到最低值。这一结果也符合莫尔-库仑强度理论关于破坏面方向的判据。由于试验中只取了3个角度，因此，数值模拟结果曲线与试验结果曲线在＝30°~60°范围内有差异。分别由数值模拟曲线和试验结果曲线对抗压强度σ_c与进行相关分析，可得如下关系式：

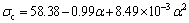        (10)

       (11)

对上述2个函数进行相关性分析，得出2个函数的相关程度指数为0.858，说明2个函数有较高的相关程度，也说明抗压试验结果能够较好地验证数值模拟的结果。

图7所示为数值模拟和试验得出的不同角度层理下的抗拉强度变化的对比曲线。由图7可知：随着的增大，抗拉强度曲线呈下降趋势；当=0°(此时拉应力作用线方向与层理面一致)时，其抗拉强度最大；当=90°(此时拉应力作用线方向与层理面垂直) 时，其抗拉强度最小。这里需要说明的是：岩石一般都含有微裂隙，在间接拉伸试验中，外加载荷都是压力，必然使部分微裂隙闭合，从而产生摩擦力，而数值模拟采用的是直接拉伸试验，不产生这种效应，故实验测得的抗拉强度比数值模拟方法所得结果要大。但数值模拟结果和试验结果的变化趋势是一致的。由数值模拟曲线和试验曲线对抗拉强度σ_c与进行相关分析，可得如下关系式：

          (12)

          (13)

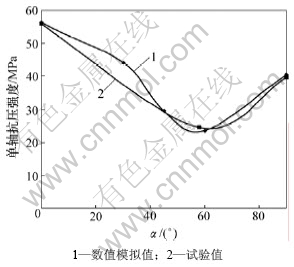
图6  单轴抗压强度随α的变化趋势

Fig.6  Correlation between uniaxial compressive strength and bedding angles

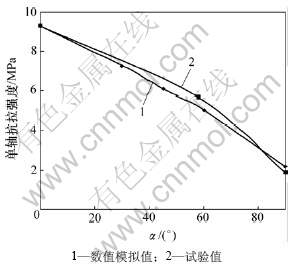
图7  单轴抗拉强度随α的变化趋势

Fig.7  Correlation between uniaxial tensile strength and bedding angles

对上述2个函数进行相关性分析，得出2个函数的相关程度指数为0.975，说明2个函数有较高的相关程度，也说明抗拉试验结果能够较好地验证数值模拟的结果。

将本文的分析结果应用到河南某金矿上覆滑坡体及采空区稳定性计算分析，解决了该工程的采空区和滑坡灾害，从而验证了本文探讨方法的合理性和可  行性。

4  结论

(1) 在单向压应力状态下，当岩体中只有一组结构面时，结构面产状与岩体抗压强度的关系如下：当结构面倾角为0°(载荷垂直结构面)时，岩体抗压强度最大；当倾角在45°到60°之间时，岩体强度最低，单轴抗压强度先减小，后增大，具有“U”型的变化趋势。σ_c与的相关分析式为： 。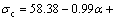

(2) 在单向拉应力状态下，随着的增大，抗拉强度随之减小，呈递减趋势。当载荷平行层理面时，抗拉强度最大；当载荷垂直层理面时，抗拉强度最小。拉应力作用方向与层理面垂直时为最不利受力状态。σ_t与的相关分析式为：。上述得出的相关式对类似材料在相近试验条件下的强度变化预测具有一定参考意义。

(3) 水平向和垂直向的岩体强度存在较大差异。单轴抗压强度的各向异性系数为0.72，抗拉强度的各向异性系数为0.24，可见抗拉强度的各向异性程度要大于抗压强度的各向异性程度。此外，岩体的变形模量也表现出明显的各向异性。上述抗压和抗拉强度随层理面倾角的变化规律与不受围压作用的单轴试验结果相符。

(4) 将本文的分析结果应用到河南某金矿上覆滑坡体及采空区稳定性计算分析中，成功地解决了该工程的采空区和滑坡灾害问题，验证了本文探讨方法的合理性和可行性，为复杂节理岩体抗拉、抗压强度的合理确定提供了一条新的途径。

参考文献：

[1] Harrison J P, Hudson J A. Engineering rock mechanics[M]. Oxford: Pergamon, 2000: 114-120.

[2] 曾纪全, 杨宗才. 岩体抗剪强度参数的结构面倾角效应[J]. 岩石力学与工程学报, 2004, 23(20): 3418-3425.
ZENG Ji-quan, YANG Zong-cai. Dip effect of structural plane on shearing strength parameters of rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3418-3425.

[3] 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002: 31-34.
CAI Mei-feng. Rock mechanics and engineering[M]. Beijing: Science Press, 2002: 31-34.

[4] 席道瑛, 陈林. 岩石各向异性参数研究[J]. 物探化探计算技术, 1994, 16(1): 16-21.
XI Dao-ying, CHEN Lin. The research of the anisotropy parameters of rock mass[J]. Geophysical and Geochemical Exploration Calculation Technology, 1994, 16(1): 16-21.

[5] 王春秋. 正交各向异性对岩体洞室破坏影响的模拟分析[J]. 岩石力学与工程学报, 2002,21(增2): 2492-2495.
WANG Chun-qiu. The simulation analysis of the effect of orthotropic to rock caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(s2): 2492-2495.

[6] 杨林德, 闫小波, 刘成学. 软岩渗透性、应变及层理关系的试验研究[J]. 岩石力学与工程学报, 2007, 26(3): 473-477.
YANG Lin-de, YAN Xiao-bo, LIU Cheng-xue. The experimental study of the relationship of soft rock permeability, bedding and strain[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 473-477.

[7] 陈运平, 王思敬, 王恩志. 循环荷载下层理岩石的弹性和衰减各向异性[J]. 岩石力学与工程学报, 2006, 25(11): 2233-2238.
CHEN Yun-ping, WANG Si-jing, WANG En-zhi. The flexibility and anisotropy decay of bedding rock mass with cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2233-2238.

[8] Fishman K L. Verification for numerical modeling of joint rock mass using thin layer element[J]. Numerical and Analytical Methods in Geomechanics, 1991, 12(15): 61-70.

[9] 黎立云, 许凤光, 高峰, 等. 岩桥贯通机理的断裂力学分析[J]. 岩石力学与工程学报, 2005, 24(23): 4328-4334.
LI Li-yun, XU Feng-guang, GAO Feng, et al. Fracture mechanics analysis of rock bridge failure mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4328-4334.

[10] 李宁, 张志强, 张平, 等. 裂隙岩样力学特性细观数值试验方法探讨[J]. 岩石力学与工程学报, 2008, 27(增1): 2848-2854.
LI Ning, ZHANG Zhi-qiang, ZHANG Ping, et al. Micro-value trial method of the mechanical properties of fractured rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(s1): 2848-2854.

[11] 刘爱华, 黄敏. 岩石弱面与岩体各向异性的力学试验研究[J]. 岩石力学与工程学报, 2008, 27(1): 152-156.
LIU Ai-hua, HUANG Ming. Study on rock joints and anisotropy of rock mass by laboratory tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 152-156.

[12] 卓家寿, 邵国建, 武清玺, 等. 力学建模导论[M]. 北京: 科学出版社, 2007: 80-84.
ZHUO Jia-shou, SHAO Guo-jian, WU Qing-xi, et al. The introduction of mechanics modeling[M]. Beijing: Science Press, 2007: 80-84.

[13] 杨强, 陈新, 周维垣. 基于二阶损伤张量的节理岩体各向异性屈服准则[J]. 岩石力学与工程学报, 2005, 24(8): 1275-1282.
YANG Qiang, CHEN Xin, ZHOU Wei-yuan. Anisotropic yield criterion for jointed rock masses based on a two-order damage tensor[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1275-1282.

[14] 张强勇, 李术才, 焦玉勇. 岩体数值分析方法与地质力学模型试验原理及工程应用[M]. 北京: 中国水利水电出版社, 2005: 62-63.
ZHANG Qiang-yong, LI Shu-cai, JIAO Yu-yong. The theory and engineering application of rock mass numerical analysis method and geomechanics model tests[M]. Beijing: China Water and Hydropower Press, 2005: 62-63.

[15] 王忠昶, 赵德深, 王怀亮. 裂纹岩体贯通机制的数值模拟研究[J]. 大连大学学报, 2007, 28(6): 32-36.
WANG Zhong-chang, ZHAO De-shen, WANG Huai-liang. Study of numerical simulation on coalescence mechanism of cracks in rock mass[J]. Journal of Dalian University, 2007, 28(6): 32-36.

[16] 张贵科. 节理岩体正交各向异性等效力学参数与屈服准则研究及其工程应用[D]. 南京: 河海大学岩土工程研究所, 2006: 56-58.
ZHANG Gui-ke. Study on equivalent orthotropic mechanical parameters and yield criterion of jointed rock mass and its engineering application[D]. Nanjing: Hohai University. Institute of Geotechnical Engineering, 2006: 56-58.

(编辑 杨幼平)

 

                                 

收稿日期：2009-10-13；修回日期：2010-01-04

基金项目：国家重点基础研究发展计划(“973”计划)项目(2007CB209402)；国家重点实验室开放基金资助项目(SKLGDUEK0906)

通信作者：刘爱华(1963-)，男，湖南邵东人，博士，教授，从事采矿工程、城市地下空间工程和岩石力学与工程方面的教学与研究；电话：13755006918；E-mail: alexliu@163.com