不同基函数对RBF-ARX模型的影响
甘敏1, 2，彭辉1
(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；
2. 合肥工业大学 电气与自动化工程学院，安徽 合肥，230009)
摘 要：研究了高斯函数、多二次函数、逆多二次函数、薄板样条函数、三次函数和线性函数对RBF-ARX模型的影响。选取Mackey-Glass混沌方程、Lorenz吸引子和Box-Jenkins煤气炉3种标准时间序列作为测试模型的数据，采用一种快速收敛的结构化非线性参数优化方法辨识RBF-ARX模型。研究结果表明：最优基函数的选择并不一定是最常用的高斯函数，而是与问题相关，因而，在实际建模中，评价各种基函数有助于选择最优结构的RBF-ARX模型。
关键词：径向基函数；RBF-ARX模型；建模
中图分类号：TP183 文献标志码：A 文章编号：1672-7207(2010)06-2231-05
Effect of different basis functions on RBF-ARX model
GAN Min1, 2, PENG Hui1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. School of Electrical Engineering and Automation, Hefei University of Technology, Hefei 230009, China)
Abstract: The effects of different basis functions including Gaussian, multiquadratic, inverse multiqudratic, thin plate spline, cubic and linear on the radial basis function network-style coefficients auto regressive model with exogenous variable (RBF-ARX) model were examined. Several benchmark time series including Mackey-Glass, Lorenz attractor and Box-Jenkins gas furnace were used as the test data. A fast-converging estimation method was applied to optimizing the RBF-ARX model parameters. The simulation results show that the optimal choice of basis function is not a normal Gaussian function but a problem dependent and evaluating all the recognised basis functions suitable for the RBF-ARX model is advantageous.
Key words: radial basis functions; RBF-ARX model; modeling
非线性系统建模问题是当前学术界研究的热点。常用的传统非线性模型为双线性模型、指数自回归模型、门限自回归模型和马尔可夫转移模型等。近年来，神经网络已成为一种流行的复杂系统建模工具[1-2]。现有的一些方法大多是单独使用传统的统计模型或神经网络模型，由Peng等[3]提出的混合结构径向基函数网络型系数的自回归模型(RBF-ARX)为非线性系统建模与控制问题提供了一种有效的解决方案，并已成功应用于非线性工业过程的建模与优化控制中，如火力发电装置的脱销过程、锅炉温度控制过程以及水箱水位控制过程[4-8]。这种模型由RBF神经网络和状态相依ARX模型相融合而成，即用一组RBF网络来逼近状态相依ARX模型中的函数系数就得到了RBF-ARX模型。在以往的研究和应用中，用来逼近状态相依ARX模型中的函数系数所用的RBF网络全是高斯核的。高斯RBF网络是一种最常用的RBF网络，然而，在某些应用中，其他形式的RBF网络可能更适合使模型性能达到最优。在此，本文作者选取高斯函数、多二次函数、逆多二次函数、薄板样条函数、三次函数和线性函数共6种被认为具有优异特性的基函数[9]的RBF网络来逼近状态相依ARX模型中的函数系数，以此来研究基函数对RBF-ARX模型性能的影响。辨识出来的模型被用来预测Mackey-Glass，Lorenz吸引子和Box-Jenkins煤气炉3种标准时间序列。
1 RBF-ARX模型
为不失一般性，采用1个非线性的单输入单输出系统，用RBF-ARX模型可表示为：
(1)
其中：y为输出；u为输入；X(t-1)为状态向量,它可能包含输入变量或输出变量，或这两者的组合，或系统中可以考虑的其他解释变量；p, q, m和nX (nX=dim{X(t-1)})均为模型的阶次；
, 
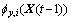(i=0, 1, …, p)和
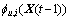(i=0, 1, …, q)是状态相依的函数系数，且各用一组RBF网络来近似；
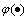为基函数；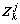
(k=1, 2, …, m; j=y, u)为RBF网络的中心；
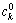(k=0, 1, 2, …, m), 
(i=1, 2, …, p; k=0, 1, 2, …, m)和
(i=1, 2, …, q; k=0, 1, 2, …, m)为RBF网络的线性权重；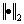
表示向量的2范式。若系统没有输入，即系数
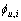全为0，则模型(1)变为了径向基函数神经网络型系数的自回归模型(RBF-AR)[10]。
RBF-ARX模型可归为RBF型的模型[3]，辨识这类模型是一个较复杂的优化问题。辨识对象包括模型的阶次，RBF网络的线性权重、中心以及比例缩放因子(或宽度)。总的来说，有3类方法来估计此类模型中的参数：第1种方法是用非线性参数优化算法(如Levenberg-Marquardt method, LMM)[11]来优化所有的参数，这种方法需搜索整个参数空间，因而计算强度大；第2种方法[12-14]是先从输入空间选取中心，然后，用最小二乘法(LSM)来估计线性权重，显然这样得到的解不是最优解；第3类方法是把参数空间分解为线性参数和非线性参数，然后，用非线性优化算法来估计非线性参数，线性优化算法来估计线性参数。此类方法可同时优化所有参数，并加快收敛速度。由Peng等[3]提出的结构化的非线性参数优化方法(SNPOM)属于第3类方法。此方法用类似于LMM 方法来优化中心，用LSM方法优化线性权重，并在搜索过程中分解参数空间结构，效果相当于压缩了参数空间，使收敛性得到了极大提高并得到了更高的精度。本文作者采用SNPOM辨识方法进行辨识。
2 基函数
模型(1)中未指明用何种类型的径向基函数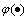，Peng等[3-8, 10]所用的都是高斯函数。事实上，有大量的径向基函数可以选择，因此，对于实际问题，径向基函数可能有优劣之分。
(1) 高斯(Gaussian)函数：
，
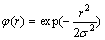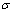＞0, r
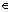R (2)
(2) 多二次(multiquadratic)函数：
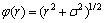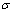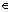，＞0, rR (3)
(3) 逆多二次(inverse multiquadratic)函数：
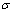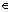，＞0, rR (4)
(4) 薄板样条(thin plate spline)函数：
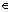，rR (5)
(5) 三次(cubic)函数：
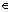，rR (6)
(6) 线性(linear)函数：
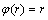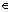，rR (7)
式(2)中的高斯函数和式(4)中的逆多二次函数为局部化的函数，因为当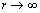
时，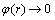
。而其他函数均为非局部性的，因为当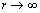时，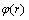
是无界的。Powell[15]的研究表明非局部性的函数能以更高的精度逼近一个光滑的输入-输出映射。
3 比较实验
选取Mackey-Glass混沌方程、Lorenz吸引子和Box-Jenkins煤气炉3种时间序列作为测试对象。每组数据均分为训练数据和检验数据2部分。将训练数据用来辨识模型，检验数据用来检验模型的性能。在所有数值实验中，评价模型的性能指标为均方误差。
3.1 Mackey-Glass时间序列
基于Mackey-Glass微分方程的混沌时间序列预测常常被认为是检验和比较各种模型性能的一个标准测试问题。用微分方程表示为：
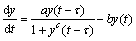(8)
选取a＝0.2，b=0.1，c=10，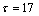
。用四阶Runge-Kutta方法来生成数据，初始值为y(0)=1.2，步长为0.1。选取1 000个如下形式的输入、输出(分号前为输入，分号后为输出)数据对：
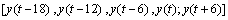
其中：t为118~1 117。以前500个数据对用来训练模型，后500个数据对用来检验模型。图1所示为Mackey-Glass时间序列。用以下RBF-AR模型来对此混沌时间序列进行建模：
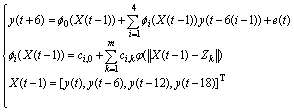(9)
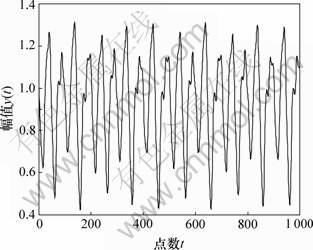
图1 Mackey-Glass时间序列
Fig.1 Mackey-Glass time series
用6种径向基函数替换式(9)中的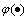，所得到的各种RBF-AR模型对Mackey-Glass时间序列的预测结果(均为最优模型情况)如表1所示。从表1可以看出：薄板样条函数的RBF-AR模型的训练数据和检验数据的均方误差最小，其检验数据均方误差为产生最大均方误差的三次函数的54.4%，为最常用的高斯函数的68.0%，而且高斯函数的模型所用节点数最多，这说明高斯RBF-AR对于此时间序列并不是最优的模型。图2所示为各种径向基函数的RBF-AR模型在不同节点数下的预测误差(检验数据)。
表1 不同径向基函数的RBF-AR模型对Mackey-Glass时间序列的预测结果比较
Table 1 Performance comparison of RBF-AR models with different basis functions for Mackey-Glass series
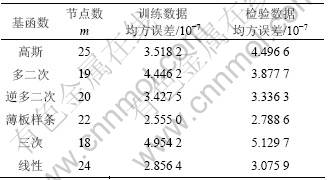
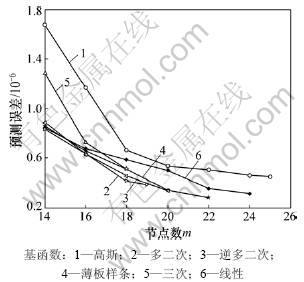
图2 Mackey-Glass时间序列预测误差的比较
Fig.2 Comparison results for Mackey-Glass time series
3.2 Lorenz吸引子时间序列
Lorenz吸引子系统可由以下微分方程表示：
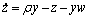
(10)
其中：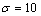
；
；
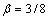。用Runge-Kutta方法解此微分方程来生成数据，步长为0.05。选取y的1 500个数据，如图3所示，前1 000个数据用来训练模型，后500个数据用来检验模型。用以下RBF-AR模型来对此时间序列进行建模：
(11)
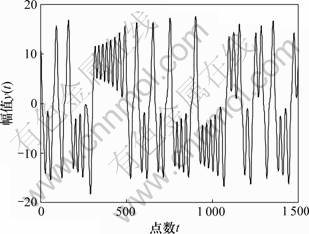
图3 Lorenz吸引子时间序列
Fig.3 Lorenz attractor time series
6种径向基函数的RBF-AR模型(11)对此时间序列的预测结果(均为最优模型情况)如表2所示。从表2可以看出：采用高斯函数、逆多二次函数、三次函数和线性函数作为基函数所得的结果相似；线性函数的预测结果最好，薄板样条函数的预测结果最差。图4所示为各种径向基函数的RBF-AR模型在不同节点数下的预测误差(检验数据)。
表2 不同径向基函数的RBF-AR模型对Lorenz吸引子时间序列的预测结果
Table 2 Performance comparison of RBF-AR models with different basis functions for Lorenz attractor time series
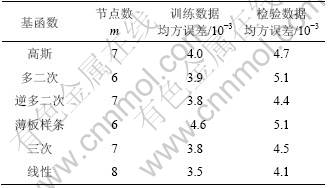
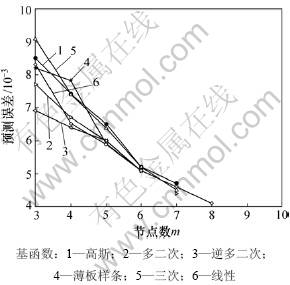
图4 Lorenz吸引子时间序列预测误差的比较
Fig.4 Comparison results for Lorenz attractor time series
3.3 Box-Jenkins时间序列
图5所示为Box-Jenkins煤气炉时间序列的296对输入-输出数据{y(t), u(t)}。输出y(t)是反应炉中产生二氧化碳的浓度，输入u(t)是输入煤气的速度。以基于[y(t-1), y(t-2), y(t-3), y(t-4), u(t-1), u(t-2), u(t-3), u(t-4), u(t-5), u(t-6)]来预测y(t)。因此，有效的数据变为290对，其中，前140对用作训练数据，后150对用作检验数据。用以下RBF-ARX模型来对此时间序列进行建模：
(12)
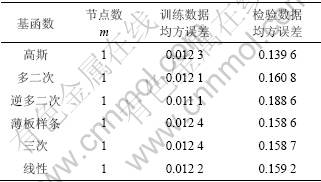
各种径向基函数的RBF-ARX模型(12)对此时间序列的预测结果如表3所示。从表3可以看出：每种径向基函数的RBF-ARX模型只用了1个节点数，它们在训练数据上的结果非常相似，然而，在检验数据上差异较大。对于此时间序列，采用高斯函数的模型取得的模型预测性能最佳。
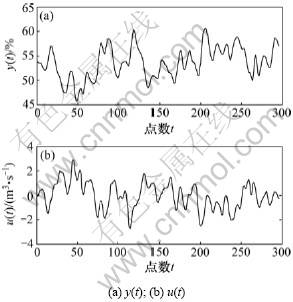
图5 Box-Jenkins时间序列
Fig.5 Box-Jenkins time series
表3 不同径向基函数的RBF-ARX模型对Box-Jenkins时间序列的预测结果
Table 3 Performance comparison of RBF-AR models with different basis functions for Box-Jenkins time series
4 结论
(1) 最优基函数的选择依赖于实际问题。最优的基函数有高斯函数、薄板样条函数和线性函数。
(2) 在实际的应用中，测试和比较不同的基函数可能会得到更优的结果，从而可以选择最优结构的RBF-ARX模型。
参考文献：
[1] 喻寿益, 王吉林, 彭晓波. 基于神经网络的铜闪速熔炼过程工艺参数预测模型[J]. 中南大学学报: 自然科学版, 2007, 38(3): 523-527.
YU Shou-yi, WANG Ji-lin, PENG Xiao-bo. Prediction model of craft parameters based on neural network during the process of copper flash smelting[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 523-527.
[2] 李彦斌, 李存斌, 宋晓华. 改进的人工智能神经网络预测模型及其应用[J]. 中南大学学报: 自然科学版, 2008, 39(5): 1054-1058.
LI Yan-bin, LI Cun-bin, SONG Xiao-hua. Prediction model of improved artificial neural network and its application[J]. Journal of Central South University: Science and Technology, 2008, 39(5): 1054-1058.
[3] PENG Hui, Ozaki T, Haggan-Ozaki V, et al. A parameter optimization method for the radial basis function type models[J]. IEEE Transactions on Neural Networks, 2003, 14(2): 432-438.
[4] PENG Hui, Ozaki T, Toyoda Y, et al. RBF-ARX model basednonlinear system modeling andpredictive control with application to a NOx decomposition process[J]. Control Engineering Practice, 2004, 12(2): 191-203.
[5] PENG Hui, YANG Zi-jiang, GUI Wei-hua, et al. Nonlinear system modeling and robust predictive control based on RBF-ARX model[J]. Engineering Applications of Artificial Intelligence, 2007, 20: 1-9.
[6] Peng H, Nakano K, Shioya H. Nonlinear predictive control using neural nets-based local linearization ARX model—stability and industrial application[J]. IEEE Transactions on Control Systems Technology, 2007, 15(1): 130-143.
[7] Peng H, Wu J, Inoussa G, PENG Hui, et al. Nonlinear system modeling and predictive using RBF nets-based quasi-linear ARX model[J]. Control Engineering Practice, 2009, 17(1): 59-66.
[8] Haggan-Ozaki V, Ozaki T, Toyoda Y. An akaike state-space controller for RBF-ARX models[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 191-198.
[9] Bishop C M. Neural networks for pattern recognition[M]. Oxford: Clarendon Press, 1995: 164-190.
[10] Shi Z, Tamura Y, Ozaki T. Nonlinear time series modeling with the radial basis function-based state-dependent autoregressive model[J]. International Journal of System Science, 1999, 30(7): 717-727.
[11] Marquardt D. An algorithm for least-squares estimation of nonlinear parameters[J]. SIAM J Appl Math, 1963, 11(2): 431-441.
[12] Moody S, Darken C. Fast learning in networks of locally-tuned processing units[J]. Neural Comput, 1989, 1(2): 281-294.
[13] Chen S, Cowan C F N, Grant P M. Orthogonal least squares learning algorithm for radial basis function networks[J]. IEEE Transactions on Neural Networks, 1991, 2(2): 302-309.
[14] Ozaki T, Sosa P V, Haggan-Ozaki V. Reconstructing the nonlinear dynamics of epilepsy data using nonlinear time series analysis[J]. Journal of Signal Processing, 1999, 3(3): 153-162.
[15] Powell M J D. Radial basis functions for multivariable interpolation: A review[C]//Mason J C, Cox M G, ed. Algorithms for Approximation. Oxford: Clarendon Press, 1987: 143-167.
(编辑 刘华森)
收稿日期：2009-10-06；修回日期：2009-12-06
基金项目：湖南省科技计划国际合作重点资助项目(2009WK2009)；国家创新研究群体科学基金资助项目(70921001)
通信作者：甘敏(1982-)，男，湖北武汉人，博士，从事复杂系统建模、进化计算及非线性时间序列分析的研究；电话：15215698383；E-mail: aganmin@yahoo.com.cn
