
Equilibrium analysis of solvent extraction of yttrium (Ⅲ) and europium (Ⅲ) from hydrochloric acid with P507
FU Nian-xin1, SUI Zhi-tong1, Mikiya Tanaka2
1. School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China;
2. Research Institute for Environmental Management Technology,
National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8569, Japan
Received 30 October 2010; accepted 27 May 2011
Abstract: For the accurate prediction of equilibrium distribution ratios of rare earth metals during solvent extraction under non-ideal conditions, the extraction equilibria of yttrium (III) and europium (III) from the hydrochloric acid solutions with P507 in Shellsol D70 were studied. A chemically-based model was established and the extraction equilibrium constants were determined by the nonlinear least squares method. The proposed model involves the cation exchange reaction and the solvation extraction in the low and high acidity regions, respectively. In the model, the nonideality of the aqueous phase and 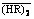 was corrected by considering the complexation of the metals with Cl- and by replacing
was corrected by considering the complexation of the metals with Cl- and by replacing  with its effective concentration, respectively. This model was verified by fair agreement between the calculated metal distribution ratios and those experimentally obtained in the single metal systems. The feed concentrations for the systems are in wide ranges of the metal (up to 0.1 mol/L), hydrochloric acid (0.07-3.00 mol/L) and the extractant (0.25-1.00 mol/L). The model enables the engineering prediction of the equilibrium distribution ratios with good accuracy in a binary metal system.
with its effective concentration, respectively. This model was verified by fair agreement between the calculated metal distribution ratios and those experimentally obtained in the single metal systems. The feed concentrations for the systems are in wide ranges of the metal (up to 0.1 mol/L), hydrochloric acid (0.07-3.00 mol/L) and the extractant (0.25-1.00 mol/L). The model enables the engineering prediction of the equilibrium distribution ratios with good accuracy in a binary metal system.
Key words: extraction; distribution ratio; yttrium; europium; model
1 Introduction
Rare earth (RE) elements which possess physically and chemically specific properties are applied in many fields of advanced technology such as laser, nuclear reactors and super conductors. The demand for rare earths is increasing nowadays in the world. It is of importance to recover rare earths from spent materials such as yttrium and europium bearing fluorescent lamp and color TV tubes. Solvent extraction is presently one of the major techniques on industrial scale for the separation and recovery of metals. This technique is characterized by outstanding effectiveness for the mutual separation of metals as well as easy and continuous operation. Particularly, the extraction of RE with acidic organophosphorus reagents is widely and increasingly employed. A number of fundamental studies of RE solvent extraction have been carried out under idealized conditions. Namely, very low metal concentrations and a constant ionic strength of the aqueous solution are kept to avoid any changes in activity coefficients of the chemical species [1-6]. KUBOTA et al [1] measured the extraction equilibria of rare earth metals in trace concentrations with P507. The extraction equilibrium constants of metals were obtained. IGLESIAS et al [6] studied the solvent extraction of yttrium from nitrate media at low metal concentration by P204. They analyzed the liquid-liquid distribution data and determined metal organic species formed during the extraction. However, practical metal extraction on a commercial scale is usually conducted under highly nonideal conditions, but few reports have been concerned with extraction equilibrium analysis of RE metals in such cases [7-9]. HIRASHIMA et al [7] presented the distribution equilibrium data for the extraction of lanthanides in macro concentrations with 1 mol/L P204 in n-heptane, and discussed the effect of some factors on the distribution equilibria.
In the present study, the extraction equilibria of yttrium and europium in the hydrochloric acid solutions by 2-ethylhexyl phosphonic acid mono-2-ethylhexyl ester (its commercial name is P507, abbreviated as HR) were examined at 298 K under the practical operating conditions. The distribution data of each metal between the aqueous and organic phases were measured at different feed concentrations of the hydrogen ion and the extractant. Based on the analysis of the observed data, an appropriate chemically-based mathematical model was established and the corresponding equilibrium constants were determined. Such a model is useful for the multistage extraction simulation to find the optimum operating conditions. The validity of the model was verified by comparing the calculated data with the observed ones. Its applicability was evaluated for the single component systems and the binary system in different feed concentrations of the metals.
2 Experimental
2.1 Reagents and solutions
P507 (Daihachi Chemicals) and Shellsol D70 (Shell Chemicals) were used as the extractant and organic diluent, respectively, without further purification. Working solutions having a given P507 concentration were prepared by adding the diluent to P507. The extractant concentration varied from 0.25 to 1.00 mol/L, which was determined by the nonaqueous neutralization titration. Unless otherwise noted, all P507 concentrations were reported on a monomer basis.
Aqueous RECl3 stock solutions were prepared by dissolving the appropriate RE2O3 (Wako, 99.99% purity, RE=Y or Eu) in excess reagent grade HCl solution, removing the surplus acid by heating on a hot plate, and then dissolving the product with 0.1 mol/L HCl solution. The RE concentrations of the stock solutions were standardized by titration with 0.01 mol/L EDTA solution at pH 5.1-5.6 using xylenol orange (XO) as the indicator, and the hydrogen ion concentrations by neutralization titration against a standardized NaOH solution, both using an AUT-501 auto-titrator (TOA). Working solutions were made up by diluting the stock solution with the HCl solution in appropriate concentrations for the feed concentrations of RECl3 from 0.005 to 0.500 mol/L and HCl from 0.07 to 3.00 mol/L. All other chemicals employed were of reagent grade purity.
2.2 Extraction procedure
Equal volumes (15 mL) of the aqueous and organic working solutions were placed in 50 mL-stoppered conical flasks, shaken for 3 h in a thermostated water bath maintained at (298±0.1) K to achieve equilibrium. The mixture was centrifuged and separated, and the aqueous and organic phases were separately pipetted. The hydrogen ion concentrations of the aqueous phase were measured by neutralization titration. The extracted species were recovered from the organic phase by back-extracting with 6 mol/L HCl. The equilibrium RE concentrations of both the aqueous and organic phases were determined by titration with 0.01 mol/L EDTA solution and by an SPS4000 plasma spectrometer (ICP-AES, Seiko) when they were relatively high and low, respectively. The distribution ratio was calculated, which was defined as the ratio of the RE concentration in the organic phase to that in the aqueous phase.
3 Results and discussion
3.1 RE extraction equilibria
The mechanism involved in the extraction of the trivalent RE elements by P204 and P507 was first described by PEPPARD et al [10-11] at low loading ratio and low acid concentration of aqueous phase. The stoichiometry of extraction, later confirmed by others [6, 9, 12-15], can be represented by a cation exchange reaction.
Assuming P507 exists as a dimer in Shellsol D70 because of a great dimerization constant Km of 2.2×104 L/mol determined in Ref. [16], the reaction for the extraction is written as:

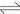
 (1)
(1)
with the apparent equilibrium constant K1
 (2)
(2)
where M, bar superscripts and bracket denote the RE, the organic species and the concentration, respectively.
If M3+ and  are the only species of RE in the aqueous and organic phases, respectively, the distribution ratio of RE, D, is described as:
are the only species of RE in the aqueous and organic phases, respectively, the distribution ratio of RE, D, is described as:
 (3)
(3)
According to Eq. (3), the relationship between the values of lg D-3lg and
and 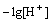 can be shown in Fig. 1 using the observed equilibrium data of the YCl3 and EuCl3 systems in the feed concentration of 0.05 mol/L Y3+ and 0.005 mol/L Eu3+, respectively, where
can be shown in Fig. 1 using the observed equilibrium data of the YCl3 and EuCl3 systems in the feed concentration of 0.05 mol/L Y3+ and 0.005 mol/L Eu3+, respectively, where  For both the systems, straight lines with a slope of 3 in the low acidity region for each
For both the systems, straight lines with a slope of 3 in the low acidity region for each  are obtained, which indicates that the extraction of RE follows Eq. (1). However, the plotted points deviate upwards from the lines with an increase in the acidity. This deviation may be interpreted as a solvation extraction of RE expressed by Eq. (4), which becomes appreciable with increasing the acid concentration. Such a tendency was also observed in the extraction of Y(III) and La(III) from the hydrochloric acid solutions with P204 [17-18].
are obtained, which indicates that the extraction of RE follows Eq. (1). However, the plotted points deviate upwards from the lines with an increase in the acidity. This deviation may be interpreted as a solvation extraction of RE expressed by Eq. (4), which becomes appreciable with increasing the acid concentration. Such a tendency was also observed in the extraction of Y(III) and La(III) from the hydrochloric acid solutions with P204 [17-18].

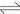
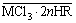 (4)
(4)
where n is the salvation number.
Also, according to Eq. (3), D is dependent upon the third power of 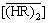 . However, on the plots of
. However, on the plots of
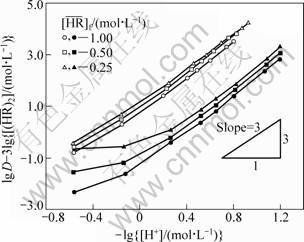
Fig. 1 lg D-3lg vs hydrogen ion concentration for extraction of RE with P507 (Open marks: YCl3, [Y3+]f=0.05 mol/L; Closed marks: EuCl3, [Eu3+]f =0.005 mol/L. [H+]f =0.07-3.00 mol/L)
vs hydrogen ion concentration for extraction of RE with P507 (Open marks: YCl3, [Y3+]f=0.05 mol/L; Closed marks: EuCl3, [Eu3+]f =0.005 mol/L. [H+]f =0.07-3.00 mol/L)
 vs
vs 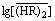 in the low acidity region ([H+]f < 1 mol/L) for the same systems, as shown in Fig. 2, the experimental points lie on a straight line with a slope less than 3 for each acid concentration. These downward deviations from the third-power dependency would be attributed to the nonideality of
in the low acidity region ([H+]f < 1 mol/L) for the same systems, as shown in Fig. 2, the experimental points lie on a straight line with a slope less than 3 for each acid concentration. These downward deviations from the third-power dependency would be attributed to the nonideality of 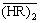 . This is caused by an increase in solute-solute interaction with raising the extractant concentration [19-20], where the interacting solute species is the P507 dimer. This nonideality can be corrected by the effective concentration of P507 dimer,
. This is caused by an increase in solute-solute interaction with raising the extractant concentration [19-20], where the interacting solute species is the P507 dimer. This nonideality can be corrected by the effective concentration of P507 dimer,  , expressed as:
, expressed as:
 (5)
(5)
The coefficient,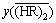 , was determined by the analysis on the extraction equilibrium data for the Y(NO3)3 system at [H+]f of 0.05 mol/L in the previous
, was determined by the analysis on the extraction equilibrium data for the Y(NO3)3 system at [H+]f of 0.05 mol/L in the previous
work [16], as shown by Eq. (6):
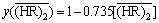 (
(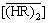 ≤0.625 mol/L)(6)
≤0.625 mol/L)(6)
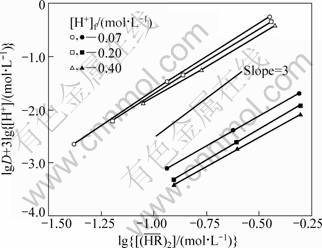
Fig. 2 lg D+3lg[H+] vs lg for extraction of RE with P507 in lower-acidity region (Open marks: YCl3, [Y3+]f =0.05 mol/L; Closed marks: EuCl3, [Eu3+]f =0.005 mol/L.
for extraction of RE with P507 in lower-acidity region (Open marks: YCl3, [Y3+]f =0.05 mol/L; Closed marks: EuCl3, [Eu3+]f =0.005 mol/L. 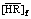 = 0.25-1.00 mol/L)
= 0.25-1.00 mol/L)
In addition, the line connecting the experimental points at each [H+]f level in Fig. 2 is located in slightly different positions from one another for both the systems; that is, the lg D+3lg[H+] values decrease with increasing [H+]f. This would be due to the formation of complexes of RE with Cl- in the aqueous phase. We assumed the formation of the first order complexes under the present experimental conditions, as defined by Eq. (7):
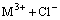
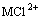 (7)
(7)
The value of stability constants, β1, was taken as 0.891 L/mol from the literature for both YCl2+ and EuCl2+ [21].
Based on all the above analysis, the distribution ratio can be calculated as follows:
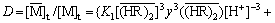
 (8)
(8)
where  and [M]t denote the total RE concentration in the organic and aqueous phases, respectively; K2 denotes the apparent equilibrium constant of Eq. (4).
and [M]t denote the total RE concentration in the organic and aqueous phases, respectively; K2 denotes the apparent equilibrium constant of Eq. (4).
The total concentration of the extractant, that is, the feed concentration of the monomeric extractant can be expressed as:


 (9)
(9)
For each value of n (=1/2, 1, 3/2, 2, …), the most suitable combinations of the values of K1 and K2 were obtained by fitting these equations together with those of the electric charge balance in the aqueous phase and the mass balance of RE and Cl- to the experimental data by the nonlinear least squares method to minimize the standard deviations in terms of D, σ, expressed by:
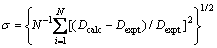 (10)
(10)
where Dcalc and Dexpt denote the calculated and observed distribution ratios of RE, respectively, and N represents the number of the experimental points. It was found that the calculated σ values were smaller when n=3 and n=1/2 than the others for YCl3 and EuCl3 systems, respectively. Thus, the most likely values of the constants were determined in this case, and are summarized in Table 1.
Table 1 Determined equilibrium constants and standard deviations

With these constants and the feed concentrations of RE, H+ and  , the distribution ratios and the equilibrium hydrogen ion concentration of the aqueous phase were calculated by the iterative method using the above equations. The observed distribution ratios are plotted against the hydrogen ion concentration of the aqueous phase shown in Fig. 3 and Fig. 4 for the YCl3 and EuCl3 systems, respectively, and are compared with the calculated values shown by curves. The agreement of the lg D values between the experiment and the prediction is well for both the systems. This indicates that the proposed model can reproduce the experimental data with good accuracy over a wide range of acidity of the aqueous phase ([H+]f=0.07-3.00 mol/L).
, the distribution ratios and the equilibrium hydrogen ion concentration of the aqueous phase were calculated by the iterative method using the above equations. The observed distribution ratios are plotted against the hydrogen ion concentration of the aqueous phase shown in Fig. 3 and Fig. 4 for the YCl3 and EuCl3 systems, respectively, and are compared with the calculated values shown by curves. The agreement of the lg D values between the experiment and the prediction is well for both the systems. This indicates that the proposed model can reproduce the experimental data with good accuracy over a wide range of acidity of the aqueous phase ([H+]f=0.07-3.00 mol/L).
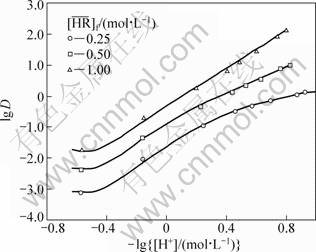
Fig. 3 Effect of equilibrium hydrogen ion concentration on distribution ratio of Y ([Y3+]f=0.05 mol/L, [H+]f=0.07-3.00 mol/L)
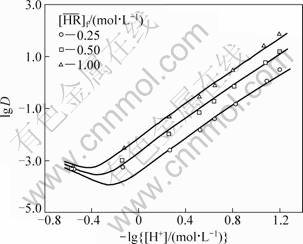
Fig. 4 Effect of equilibrium hydrogen ion concentration on distribution ratio of Eu ([Eu3+]f = 0.05 mol/L, [H+]f=0.07-3.00 mol/L)
In this modeling, the changes in the activity coefficients of aqueous RE and hydrogen ions were not fully considered. Although these points can be overcome by employing an estimation method of the activity coefficients, the parameters required for the estimation are often unavailable. This will lead to a very complex model. In the present work, therefore, we have avoided such an approach for the engineering purpose. In this viewpoint, the constants given in Table 1 are specific and should be used in caution.
3.2 Applicability of model to different metal concentrations
The extraction of RE was studied with extending the feed concentrations of RE from 0.01 to 0.5 mol/L as a function of the initial aqueous acidity at  =0.5 mol/L in order to evaluate the applicability of the proposed model to different metal concentrations. The observed distribution ratios were consistent with the respective calculated curves obtained by the iterative method for [M3+]f=0.01 and 0.1 mol/L as shown in Fig. 5, but deviate upwards from those for [Y3+]f=0.5 mol/L in Fig. 6. These results indicate that the model is applicable for the RE feed concentrations at least up to 0.1 mol/L. The evident difference of the prediction from the observed data at high [M3+]f, corresponding to a high loading ratio, may be explained in terms of the formation of polymeric species [6, 22-23]:
=0.5 mol/L in order to evaluate the applicability of the proposed model to different metal concentrations. The observed distribution ratios were consistent with the respective calculated curves obtained by the iterative method for [M3+]f=0.01 and 0.1 mol/L as shown in Fig. 5, but deviate upwards from those for [Y3+]f=0.5 mol/L in Fig. 6. These results indicate that the model is applicable for the RE feed concentrations at least up to 0.1 mol/L. The evident difference of the prediction from the observed data at high [M3+]f, corresponding to a high loading ratio, may be explained in terms of the formation of polymeric species [6, 22-23]:

 (11)
(11)
where m denotes the degree of polymerization.
3.3 Extraction of binary metal system
The proposed model with the extraction of the single metal systems was extended to the binary metal Y-Eu system to examine its applicability. Assuming the interaction between the two metals is negligible [9], the following equations of the mass balance for the binary metal extraction are expressed.
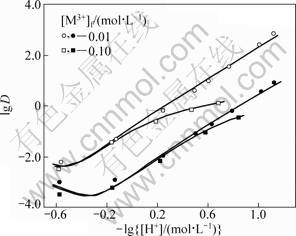
Fig. 5 Distribution ratio of RE vs hydrogen ion concentration for different [M3+]f (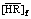 =0.5 mol/L; Open marks: YCl3; Closed marks: EuCl3. [H+]f =0.07-3.00 mol/L)
=0.5 mol/L; Open marks: YCl3; Closed marks: EuCl3. [H+]f =0.07-3.00 mol/L)
Fig. 6 Distribution ratio of RE vs hydrogen ion concentration in RECl3 systems for [RE3+]f=0.5 mol/L ( =0.5 mol/L, [H+]f=0.07-3.00 mol/L)
=0.5 mol/L, [H+]f=0.07-3.00 mol/L)
For the chloride ion,

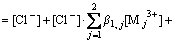
 (12)
(12)
where (j=1, 2) represents the items for Y and Eu, respectively.
For the extractant,
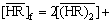

 (13)
(13)
With the obtained equilibrium constants and the feed concentrations of all the solutes, the distribution ratios of RE as a function of the hydrogen ion concentration of the aqueous phase were calculated by the iterative method using the above equations together with those of the electric charge balance in the aqueous phase and the mass balance of the metals. The experimental data obtained under the conditions that [Y3+]f=0.05 mol/L and [Eu3+]f=0.005 mol/L as a function of  (0.25 to 1 mol/L) and [H+]f (0.07 to 3 mol/L) are plotted in Fig. 7 and Fig. 8. They are compared with the calculated values shown by the curves in the figures, which show a fair agreement between both of them. This indicates that the model obtained with the single metal systems is applicable to the extraction prediction of the binary metal system over a wide range of acidity.
(0.25 to 1 mol/L) and [H+]f (0.07 to 3 mol/L) are plotted in Fig. 7 and Fig. 8. They are compared with the calculated values shown by the curves in the figures, which show a fair agreement between both of them. This indicates that the model obtained with the single metal systems is applicable to the extraction prediction of the binary metal system over a wide range of acidity.
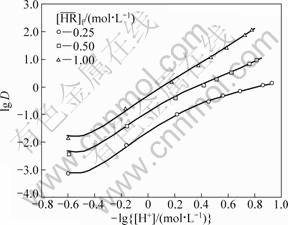
Fig. 7 Effect of hydrogen ion concentration on distribution ratio of Y in binary system ([Y3+]f=0.05 mol/L, [Eu3+]f=0.005 mol/L, [H+]f=0.07-3.00 mol/L)
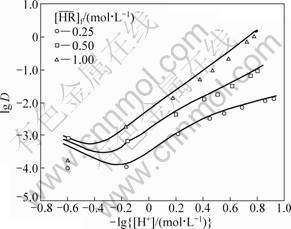
Fig. 8 Effect of hydrogen ion concentration on distribution ratio of Eu in binary system ([Y3+]f=0.05 mol/L, [Eu3+]f=0.005 mol/L, [H+]f=0.07-3.00 mol/L)
4 Conclusions
1) A chemical equilibrium model was established by analyzing the distribution data of the single metal systems ([Y3+]f=0.05 mol/L or [Eu3+]f=0.005 mol/L) over wide feed concentration ranges of hydrochloric acid (0.07-3.00 mol/L) and the extractant (0.25-1.00 mol/L). The extraction equilibrium constants were determined by fitting the model to the experimental data using the nonlinear least squares method. The extraction equilibria involve the cation exchange reaction in the low acidity region and the solvation extraction in the high acidity region. Also, the nonideality of the aqueous phase and 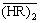 was corrected by considering the complexation of RE with Cl- and by replacing
was corrected by considering the complexation of RE with Cl- and by replacing 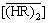 with its effective concentration, respectively.
with its effective concentration, respectively.
2) The model enables the experimental data reproduction with good accuracy in the binary metal Y-Eu system over a wide range of acidity, as well as in the single metal systems for the feed concentrations of RE up to 0.1 mol/L.
References
[1] KUBOTA F, GOTO M, NAKASHIO F. Extraction of earth metals with 2-ethylhexyl phosphonic acid mono-2-ethylhexyl ester in the presence of diethylenetriaminepentaacetic acid in aqueous phase [J]. Solvent Extr Ion Exch, 1993, 11(3): 437-453.
[2] MASON G W, METTA D N, PEPPARD D F. The extraction of selected M(Ⅲ) metals by dis 2-ethylhexyl phosphoric acid in n-heptane [J]. J Inorg Nucl Chem, 1976, 38(11): 2077-2079.
[3] CECCAROLI B, ALSTAD J. Trends in separation factors for the lanthanum series as obtained in solvent extraction from an aqueous thiocyanate solution [J]. J Inorg Nucl Chem, 1981, 43(8): 1881-1886.
[4] KANDIL A T, FARAH K. The solvent extraction of terbium and europium by di-(2-ethylhexyl)- phosphoric acid and various organophosphorous compounds [J]. J Inorg Nucl Chem, 1980, 42(2): 277-280.
[5] MORI Y, OHYA H, ONO H, EGUCHI W. Extraction equilibrium of Ce(Ⅲ), Pr(Ⅲ) and Nd(Ⅲ) with acidic organophophorus extractants [J]. J Chem Eng Jpn, 1988, 21(1): 86-91.
[6] IGLESIAS M, ANTIC? E, SALVAD? V, MASANA A, VALIENTE M. Effect of Y(III) distribution between aqueous nitrate and organic D2EHPA solutions on the Y(III) precipitation stripping using oxalic acid [J]. Solvent Extr Ion Exch, 1999, 17(2): 277-300.
[7] HIRASHIMA Y, MUGITA M, SHIOKAWA J. Distribution equilibria of SmCl3-EuCl3-HCl and EuCl3- GdCl3-HCl systems with 1M di(2-ethylhexyl)phosphoric acid in n-heptane [J]. J Inorg Nucl Chem, 1975, 37(5): 1249-1253.
[8] LENZ T G, SMUTZ M. The extraction of neodymium and samarium by di(2-ethylhexyl) phosphoric acid from aqueous chloride, perchlorate and nitrate systems [J]. J Inorg Nucl Chem, 1968, 30(2): 621-637.
[9] HINO A, NISHIHAMA S, HIRAI T, KOMASAWA I. Practical study of liquid-liquid extraction process for separation of rare elements with dis(2-ethylhexyl)phosphinic acid [J]. J Chem Eng Jpn, 1997, 30(6): 1040-1046.
[10] PEPPARD D F, MASON G W, DRISCOLL W J, SIRONEN R J. Acidic esters of orthophosphoric acid as selective extractants for metallic cations-tracer studies [J]. J Inorg Nucl Chem, 1958, 7(3): 276-285.
[11] PEPPARD D F, MASON G W, HUCHER I. Acidic esters of phosphoric acid as selective extractants for metallic cations-selected M(III) tracer studies [J]. J Inorg Nucl Chem, 1961, 18: 245-258.
[12] GEIST A, NITSCH W, KIM J. On the kinetics of rare-earth extraction into D2EHPA [J]. Chem Eng Sci, 1999, 54(8): 1903-1907.
[13] LI De-qian, ZHANG Jie, XU Min. Studies of extraction mechanism of rare earth compounds with mono(2-ethyl hexyl)2-ethyl hexyl phosphonate (HEH[EHP]) I. The distribution of rare earth compounds in the system HNO3-H2O-HEH[EHP] and the effect of temperatures and solvents [J]. Chinese Journal of Applied Chemistry, 1985, 2(2): 17-23. (in Chinese)
[14] MA En-xin, YAN Xiao-min, WANG San-yi. Chemistry of lanthanoids solvent extraction with 2-ethylhexyl phosphonic acid mono-2-ethylhexyl ester [J]. Science in China, Ser A, 1981(5): 565-573. (in Chinese)
[15] XU Guang-xian. Rare earths [M]. Beijing: Metallurgical Industry Press, 1995: 525-528. (in Chinese)
[16] FU Nian-xin, TANAKA M. Modeling of solvent extraction of yttrium (III) and europium (III) from nitric acid with PC-88A [J]. Materials Transactions, 2006, 47(1): 136-142.
[17] SATO T, UEDA M. The extraction of yttrium (III) and lanthanum (III) from hydrochloric acid solutions by di(2-ethylhexyl)phosphoric acid [J]. J Inorg Nucl Chem, 1973, 35: 1003-1010.
[18] HIRASHIMA Y, YAMAMOTO Y, TAKAGI S, AMANO T, SHIOKAWA J. Extraction of lanthanoids from hydrochloric and nitric acid solutions by di(2-ethylhexyl)phosphoric acid [J]. Bull Chem Soc Jpn, 1978, 51(10): 2890-2893.
[19] ALSTAD J, AUGUSTSON J H, DANIELSSEN T, FARBU L. Comparative study of the rare earth elements in extraction by HDEHP/shellosol T from nitric and sulfuric and solutions [C]//Proceedings of the international solvent extraction conference. Lyons, France: ISEC, 1974: 1083-1102.
[20] DANESI P R, VANDEGRIFT G F. Activity coefficients of bis(2-ethylhexyl)phosphoric acid in n-dodecane [J]. Inorg Nucl Chem Letters, 1981, 17(3): 109-115.
[21] LARS G S, ARTHUR E M. Stability constants of metal-ion complexes [M]. London: The Chem Society, 1964: 274.
[22] HIRASHIMA Y, KODERA H, SHIOKAWA J. Extraction of lanthanoids with bis(2-ethylhexyl) hydrogenphosphate-equilibria in the region of high loading [J]. Nippon Kagakukaishi, 1982, 4: 627-631.
[23] INOUE K, BABA Y, YOSHIZUKA K. Equilibria in the solvent extraction of indium(III) from nitric acid with acidic organophosphorus compounds [J]. Hydrometallurgy, 1988, 19(3): 393-399.
盐酸液中钇(Ⅲ)和铕(Ⅲ)的P507溶剂萃取平衡分析
付念新1,隋智通1,Mikiya Tanaka2
1. 东北大学 材料与冶金学院, 沈阳 110004;
2. Research Institute for Environmental Management Technology,
National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8569, Japan
摘 要:为了精确预测非理想条件下稀土金属溶剂萃取的平衡分配比,研究了溶于shellsol D70中的P507溶剂对盐酸液中钇(III)和铕(III)的萃取平衡,建立化学基模型,并通过非线性最小二乘法确定萃取平衡常数。所建模型涉及了在低酸度区的离子交换反应和高酸度区的溶剂化萃取反应;模型还考虑了稀土金属与Cl-的配位反应,并用萃取剂的有效浓度代替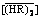 ,进而分别对水相和有机相
,进而分别对水相和有机相 的非理想性加以修正。对稀土单元体系,在较宽的初始浓度范围内(稀土浓度最高至0.1 mol/L,盐酸浓度0.07-3.00 mol/L,萃取剂浓度0.25-1.00 mol/L),由模型计算的稀土分配比与实验测得的数据吻合良好,验证了模型的有效性。对于稀土二元体系,该模型能以良好的精度对平衡分配比进行工程预测。
的非理想性加以修正。对稀土单元体系,在较宽的初始浓度范围内(稀土浓度最高至0.1 mol/L,盐酸浓度0.07-3.00 mol/L,萃取剂浓度0.25-1.00 mol/L),由模型计算的稀土分配比与实验测得的数据吻合良好,验证了模型的有效性。对于稀土二元体系,该模型能以良好的精度对平衡分配比进行工程预测。
关键词:萃取;分配比;钇;铕;模型
(Edited by LI Xiang-qun)
Foundation item: Project (P02426) supported by the Japan Society for the Promotion of Science for Postdoctoral Fellowships for Foreign Researchers
Corresponding author: FU Nian-xin; Tel: +86-24-83681310; Fax:+86-24-23906316; E-mail: funx@smm.neu.edu.cn
DOI: 10.1016/S1003-6326(11)60978-3