DOI: 10.11817/j.issn.1672-7207.2015.07.041

湖南省高速公路路面使用性能衰变模型

肖金平^{1, 2}，韦慧¹，赵健¹，李振存¹

(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410076；

2. 湖南省高速公路管理局，湖南 长沙，410001)

摘要：为科学掌握高速公路路面使用性能衰变规律，合理预测大修年限，以已积累的湖南省连续10 a近1 000 km高速公路路面使用性能数据为基础，分析得到湖南省高速公路路面损坏状况指数和路面行驶质量指数大致呈反“S”型曲线规律衰减。基于此，提出能够描述衰变模式的余弦函数路面使用性能衰变模型，并研究模型参数的数学与物理意义。研究结果表明：模型参数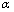与路面大修年限具有良好的一致性；将余弦函数路面使用性能衰变模型用于评价高速公路路面损坏状况以及路面行驶质量，并对其进行拟合，拟合得到的大修年限与实际大修年限基本吻合，验证了该模型的有效性和实用性。

关键词：道路工程；高速公路；衰变模型；使用性能预测

中图分类号：U416.216             文献标志码：A         文章编号：1672-7207(2015)07-2686-07

Decay model of Hunan expressway pavement performance

XIAO Jinping^{1, 2}, WEI Hui¹, ZHAO Jian¹, LI Zhencun¹

(1. School of Traffic and Transportation Engineering, Changsha University of Science & Technology,

Changsha 410076, China;

2. Hunan Expressway Administration Bureau, Changsha 410001, China)

Abstract: In order to master decay law of the expressway pavement performance, and reasonably predict the overhaul period, pavement surface condition index and riding quality index which decayed roughly “anti-S-curve” were obtained, based on the test data accumulated from nearly a 1 000 km for 10 years in Hunan expressway pavement performance. The new cosine function model of pavement performance degradation was put forward，and the mathematical and physical meaning of model parameters were studied. The results show that model parameter 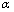 has good consistency with the overhaul period of the road. The cosine function model of pavement performance degradation can be applied to evaluate expressway pavement surface condition and riding quality condition, which is consistent with the actual overhaul period, and the correctness and practicability of the model are verified.

Key words: road engineering; expressway; decay model; performance prediction

在交通荷载和环境因素的共同作用下，路面会逐渐出现不同程度的损坏，路面的行驶舒适性和服务水平将不断降低。为表征这种衰变程度，路面使用性能作为一种评价指标被国内外学者提出，在我国也得到了广泛应用^[1-7]。我国JTG H20—2007“公路技术状况评定标准”提出了沥青路面以路面损坏状况指数(PCI)、路面行驶质量指数(RQI)、路面车辙深度指数(RDI)、路面抗滑性能指数(SRI)等反映路面的使用性能，并规定了相应的检测频率^[8]。关于路面使用性能衰变规律的研究，国内外开展了一些富有成效的研究工作^[9-10]。AASHO试验以服务能力指数(PSI)与累计轴载作用次数的幂函数关系表征路面使用性能^[11]，加拿大Alberta省提出了一种能考虑温度修正的平整度衰变模型，美国的Idaho、Washington和Arizona州都基于本州的检测数据建立了各自的路面使用性能衰变模型^[12]；孙立军等^[13-14]在分析国内外路面使用性能曲线的基础上提出了数学和物理含义明确的路面使用性能标准衰变方程。由以上研究结果可以看出：不同地区和不同路面结构的路面使用性能的衰变规律所适用的衰变模型不同。为此，本文作者在已有研究的基础上，针对湖南省高速公路路面使用性能衰变规律，以已积累的湖南省连续10 a近1 000 km高速公路路面使用性能数据为基础，进行路面使用性能衰变模型研究，并标定相关参数，以期掌握湖南省高速公路路面中长期性能，以便为路面养护维修规划提供参考。

1  湖南省高速公路路面使用性能衰变规律

高速公路路面使用性能指标主要包括路面损坏状况指数(PCI)、路面行驶质量指数(RQI)、路面车辙深度指数(RDI)和路面抗滑性能指数(SRI)等指标，不同路面表现出不同的衰变特征。结合湖南省高速公路路面类型、交通荷载等级、结构厚度和混合料类型等对路面中长期性能产生的重要影响，本文将湖南省现有高速公路划分为8种典型路面结构，如表1所示。

以已积累的湖南省连续10 a近1 000 km高速公路路面使用性能数据为基础，考虑到高速公路每年均采取各种全局性养护处治措施对损坏较严重的路面进行处治。有处治历史路段的路面性能数据不具代表性，因此，在进行统计分析时予以剔除，仅对日常养护状态下的路面进行分析。各路段路面使用性能衰变曲线如图1~4所示。

由图1和图2可知：我省典型沥青路面结构在通车运营的前3~4 a内路面损坏状况指数(PCI)衰变缓慢，而在2008年出现了快速的衰减，其中临长AK-16、耒宜AK-13、潭邵宽域沥青AK-13路面衰变速度较快，降幅在15左右；而临长SMA-16、衡枣SMA-13、长潭复合路面SMA-16以及潭邵重交沥青路面衰变速度相对缓慢，至2012年总体降幅为7~12，路面损坏状况仍较好。水泥路面前期衰变较慢，通车运营4~5 a后路面损坏状况指数(PCI)衰变速度加快。总体而言，沥青路面和水泥路面路面损坏状况指数(PCI)衰变曲线大致呈反“S”型曲线。

由图3和图4可知：湖南省典型沥青路面和水泥路面行驶质量指数(RQI)变化规律总体上呈反“S”型曲线，水泥路面平整度衰变速度较沥青路面快，其中长益高速公路水泥路面平整度衰减幅度最大，这主要是长益高速公路开通时间较早、累计轴载次数大、路面结构未设置传力钢筋和路面结构相对较差所致。

表1  湖南省高速公路典型路面结构

Table 1  Typical pavement structures of expressway in Hunan

图1  湖南省高速公路沥青路面路面损坏状况指数衰变曲线

Fig. 1  Decay curves of pavement surface condition index of asphalt pavement performance of expressway in Hunan

图2  湖南省高速公路水泥路面路面损坏状况指数衰变曲线

Fig. 2  Decay curves of pavement surface condition index of cement pavement performance of expressway in Hunan

2  路况数据的处理

路况数据是路面使用性能预测的基础。目前，各因素对路面使用性能衰变的影响难以完全划分清楚，没有一种模型能够达到完全满意的程度。路况数据采集在一定条件下进行，路况变化的随机性和采集数据时的人为影响因素，使采集的路况数据存在一定误差^[15]。为此，在进行路况数据统计分析时，应剔除离散性大的数据。

图3  湖南省高速公路沥青路面行驶质量指数衰变曲线

Fig. 3  Decay curves of riding quality index of asphalt pavement performance of expressway in Hunan

图4  湖南省高速公路水泥路面路面行驶质量指数衰变曲线

Fig. 4  Decay curves of riding quality index decay law of cement pavement performance of expressway in Hunan

偏最小二乘法可以较好地处理变量间存在多重相关性的问题。因此，考虑利用偏最小二乘法对路面使用性能影响因素进行主成分分析，并基于T2椭圆图对离散性较大的数据进行识别，其分析方法及操作步骤如下。

设有n组数据样本，已知因变量y和自变量X，则有：

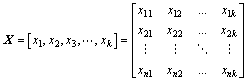      (1)

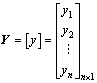              (2)

对X和Y进行标准化处理：

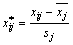；i=1, 2, …, n；j=1, 2, …, k      (3)

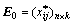；         (4)

式中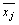：为x_j的均值；s_j为x_j的标准差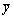；为y的均值；s_y为y的标准差。

已知E₀，从E₀中提取第1个成分t₁，计算协方差矩阵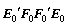最大特征值相应的单位特征向量。对

于单位向量w₁，有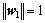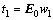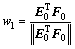，，，计算E₀和F₀对t₁的回归方程：

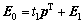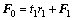；         (5)

回归系数向量以及残差矩阵E₁和F₁为：

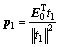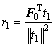 ；           (6)

；

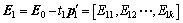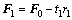                 (7)

为检验该算法的有效性，采取如下方法：若回归方程满足精度要求，则计算停止；否则，用E₁替换E₀，F₁替换F₀。采用上述方法进行第2个成分t₂的提取和回归分析，直到达到精度要求为止，提取m个主成分。

控制椭圆常用来判别造成系统异动的特殊原因。控制椭圆可构造包含2个变量的控制域，通常2个主成分可概括数据的大部分信息^[16]。设t₁和t₂为提取的前2个主成分，通过样本数据对成分的贡献率来判别异常数据。

文献[17-18]定义第i个样本数据对第h主成分t_h的贡献率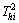为

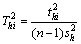               (8)

则累计贡献率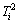为

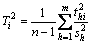             (9)

若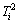过大，则说明该样本数据对回归模型有明显的拉伸。Tracy给出的统计量为

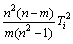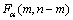~        (10)

则对于2个主成分的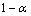置信椭圆可表示为

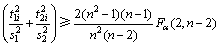    (11)

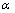取0.05，令

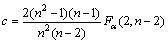       (12)

则有

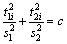             (13)

在二维平面图上作出椭圆图，当所有样本点落在控制椭圆内时，可认为样本数据里不存在离散性较大的数据；若样本数据落在控制椭圆之外，则认为是异常数据，应予以剔除。

3  路面使用性能衰变模型

3.1  衰变模型表达式

1个良好的路面使用性能衰变模型应该具备以下基本条件：

1) 具备足够的数据基础。

2) 符合路面使用性能衰变的边界条件，即初始时刻路面使用性能趋于100，当路面使用年限趋向于无穷大时路面使用性能趋于0。

3) 模型函数单调递减。

4) 模型能反映路面使用性能的实际衰变规律，拟合度良好。

5) 模型参数具有一定的物理意义，便于后续工作的开展。

根据上述基本条件并结合湖南省高速公路路面使用性能衰变规律特点，综合国内外研究成果，运用余弦函数进行大量数据拟合。本文以路面损坏状况指数和路面行驶质量指数作为预测指标，建立路面损坏和路面行驶质量衰变模型如下：

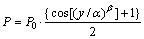         (14)

式中：P为任意时刻的路面损坏状况指数或路面行驶质量指数；P₀为初始路面使用性能指数；y为路龄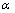；和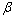为模型待定参数，均大于0，待定参数值通过对原始数据进行回归分析得到。

该模型形式简单，以使用年限(路龄)作为唯一变量。模型中的余弦曲线为周期性曲线，为使模型曲线单调递减，规定了时间y的取值范围，时间的最大值是路面名义使用寿命。经大量数据试算，该模型适用于绝大多数路面的使用寿命周期，仅不适用于因施工质量过差和路面使用寿命极短的路面。

图5所示为利用式(14)绘出的路面使用性能衰变曲线。由图5可见：本文提出的路面使用性能衰变模型能够拟合反“S”型曲线和凹曲线2种形式。反“S”型曲线一般是路面使用性能的正常衰变模式，由于新建路面在投入使用后的一段时间内，结构抗力较强，路面使用性能衰变速度缓慢，随后衰变速度加快。若在衰变速度加快前加强养护，则衰变速度变缓，曲线呈反“S”型。而凹曲线的衰变模式主要是施工质量不好或其他地质因素影响，导致路面使用性能初期衰变较快，而后衰变速度逐渐放缓。从湖南省多年养护检测数据统计分析得出的路面使用性能衰变规律来看，反“S”型曲线衰变是路面使用性能衰变的主要模式，而凹曲线模式主要适用于有先天性质量问题的路面，这类路面较少。

3.2  模型参数的数学意义

式(14)主要包括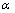和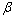这2个待定参数，具有一定的数学和物理意义。令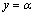，代入式(14)，可以得到

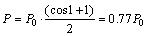          (15)

由式(15)可知：当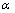一定时，无论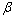如何变化，路面使用性能衰变曲线始终经过0.77P₀，即路面使用性能衰变到77%所需时间一致。为了说明这一问题，令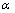=10，改变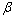，得到路面使用性能衰变曲线族，如图6所示。

由图6可以看出：当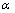为10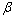，从0.50到1.50之间变化时，各类衰变曲线均经过(10，77)。曲线因变量P分布在0~100。对于运营的高速公路而言，一般要求路面使用性能不能低于标准值，否则就需中修或大修。国内外相关资料表明，高速公路一般不会因为路面结构强度不足而需要大修，大多是由于路面破损严重、路面平整度较差这类一般性维修难以解决的问题。换言之，路面需要整体大修改建的路面损坏状况指数和路面行驶质量指数一般在中等水平，即70~80，即曲线的P_min以下的曲线段基本不会用到。因此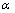，的数学含义可以认为是路面使用性能衰减到77%时的路面使用时间。根据多条高速公路的调查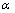，取值一般为3~15 a。

图5  不同模型参数下路面使用性能衰变规律

Fig. 5  Decay curves of pavement performance of different model parameters

图6  α一定时路面性能衰变曲线族

Fig. 6  Decay curves of pavement performance under a certain α

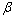主要起改变曲线形状的作用。从图5(a)和 5(b)可见：当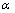=8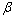，=1.25时，路面使用性能衰变曲线为反“S”型曲线；而当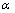=8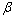，=0.50时，路面使用性能衰变曲线变为凹曲线。这说明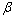对路面使用性能衰变曲线的形状具有决定作用；当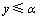时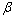，≤1.00，此时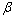越小，路面使用性能衰变的速度越快，且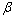＞0.30；而当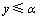时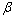，≥1.00，此时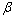，越大，路面使用性能衰变的速度越慢。从大量实测数据来看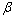，≤2.00，经综合得到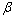的取值范围为[0.30, 2.00]。

影响路面使用性能的因素包含温度、湿度、交通荷载、路面结构、养护成本和施工质量等，所有影响路面使用性能的因素都将影响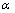和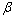。(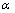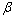，)的变化规律可综合反映不同地区、路面结构和交通荷载等影响下的路面使用性能衰变规律。

综上所述，路面使用性能衰变模型可由式(14)表示，模型中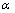和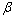由路面性能检测数据回归计算可得，拟合精度受到路面使用性能指标数据样本数量的影响。

4  模型应用算例

以湖南省某高速公路为例，收集该高速公路路面损坏状况指数和路面行驶质量指数自开通以来的路面使用性能检测数据进行回归计算，并与文献[12-13]提出的预测方程进行比较，如图7所示。

由图7可知：本文模型与文献[12-13]中的标准衰变方程拟合精度均较高，2个模型在0~8 a的路面损坏状况指数和路面行驶质量指数相差不大。但是路龄达到8 a以后，本文模型的路面性能衰变曲线仍然保持一定的衰变速度，而文献[12-13]提出的衰变方程的路面性能衰变速度变缓。根据本文提出的模型，在  11.39 a时该高速公路该路段将面临大修，而根据文献[12-13]中的模型要到18.5 a才达到大修标准。该高速公路规划在2014年大修，与按本文模型得到的大修年限基本吻合。

图7  路面使用性能预测图

Fig. 7  Prediction diagrams of pavement preformance

5  结论

1) 基于多年实测数据分析湖南省高速公路路面损坏状况指数和路面行驶质量指数衰变规律，获得衰变规律大致呈反“S”型曲线衰减。

2) 提出了能够描述衰变模式的余弦函数路面使用性能衰变模型，模型参数具有较明显的数学和物理意义，通过模型参数可预测路面大修时间。

3) 本文采用的余弦函数模型曲线均通过(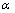，0.77P₀)，将路面损坏状况指数和路面行驶质量指数衰减至77所需的时间定义为高速公路路面使用寿命更加符合高速公路路面使用性能实际情况。

4) 将模型应用于实际工程，拟合结果与实测结果较吻合。与广泛应用的指数模型对比，本模型的拟合效果更佳，对路面使用寿命的预估更符合实际。

参考文献：

[1] Kettil P, Lenhof B, Runesson K, et al. Simulation of inelastic deformation in road structures due to cyclic mechanical and thermal loads[J]. Computers & Structures, 2007, 85(1): 58-70.

[2] 杨书祥, 马士宾. 沥青路面结构可靠性分析与维修[M]. 北京: 中国建材工业出版社, 2010: 1-15.

YANG Shuxiang, MA Shibin. Structural reliability analysis and maintenance of asphalt pavement[M]. Beijing: China Building Materials Press, 2010: 1-15.

[3] 姚祖康. 路面管理系统[M]. 北京: 人民交通出版社, 1993: 55-74.

YAO Zukang. Pavement management system[M]. Beijing: China Communications Press, 1993: 55-74.

[4] 曾胜, 黄雄立. SMA路面长期性能的调查分析及预测[J]. 长沙理工大学学报(自然科学版), 2010, 7(1): 12-17.

ZENG Sheng, HUANG Xiongli. Investigation and prediction research on long-term performance of SMA pavement[J]. Journal of Changsha University of Science and Technology (Natural Science), 2010, 7(1): 12-17.

[5] Sean C, Eric D, Yusuf M, et al. Determining the impact of degree of blending and quality of reclaimed asphalt pavement on predicted pavement performance using pavement ME design[J]. Construction and Building Materials, 2013, 48: 473-478.

[6] XU Qinwu, George K C, Victor L G, et al. Influences of intelligent compaction uniformity on pavement performances of hot mix asphalt[J]. Construction and Building Materials, 2012, 30: 746-752.

[7] Karthik D, Saman S, David J O, et al. Effects of pavement conditions on effective structural number of in-service pavements[C]// Transportation & Development Institute of ASECE. Airfield and Highway Pavement, Los Angele, 2013: 362-372.

[8] JTG H20—2007, 公路技术状况评定标准[S].

JTG H20—2007, Highway performance assessment standards[S].

[9] 孙立军, 许志军, 陈子建. 沥青路面的行为函数[J]. 同济大学学报, 2003, 31(5): 558-560.

SUN Lijun, XU Zhijun, CHEN Zijian. Behavior modeling for asphalt pavements[J]. Journal of Tongji University, 2003, 31(5): 558-560.

[10] 秦志斌, 钱国平, 马文彬. 基于熵权的沥青路面使用性能多目标综合评价[J]. 中南大学学报(自然科学版), 2013, 44(8): 3474-3476.

QIN Zhibin, QIAN Guoping, MA Wenbin. Multi-objective comprehensive evaluation for performance of asphalt concrete pavement based on fuzzy entropy[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3474-3476.

[11] National cooperative highway research program. AASHTO guide for design of pavement structures[R]. Washington AASHTO, 1993: 9-22.

[12] 孙立军. 沥青路面结构行为理论[M]. 北京: 人民交通出版社, 2005: 404-424.

SUN Lijun. Structural behavior study for asphalt pavements[M]. Beijing: China Communications Press, 2005: 404-424.

[13] 孙立军, 刘喜平. 路面使用性能的标准衰变方程[J]. 同济大学学报, 1995, 2(5): 512-517.

SUN Lijun, LIU Xiping. General deterioration epuation for pavement performance[J]. Journal of Tongji University, 1995, 2(5): 512-517.

[14] 张占军, 王笑风. 沥青路面使用性能的双参数修正预测模型[J]. 交通运输工程学报, 2007, 7(5): 54-57.

ZHANG Zhanjun, WANG Xiaofeng. Service performance prediction model of asphalt pavement with two corrected parameters[J]. Journal of Traffic and Transportation Engineering, 2007, 7(5): 54-57.

[15] 刘伯莹, 姚祖康. 沥青路面使用性能预测[J]. 中国公路学报, 1991, 4(2): 5-15.

LIU Boying, YAO Zukang. Performance prediction model for asphalt pavement[J]. China Journal of Highway and Transport, 1991, 4(2): 5-15.

[16] 韦灼彬, 吴森, 张宁. 基于振动传递率的钢框架损伤识别试验研究[J]. 防灾减灾工程学报, 2012, 32(6): 700-705.

WEI Zhuobin, WU Sen, ZHANG Ning. Experimental study on a steel frame based on vibration transmissibility[J]. Journal of Disaster Prevention and Mitigation Engineering, 2012, 32(6): 700-705.

[17] 李寿安, 张恒喜, 李东霞, 等. 基于偏最小二乘回归的军用飞机采购价格预测[J]. 海军工程大学学报, 2005, 17(4): 65-66.

LI Shouan, ZHANG Hengxi, LI Dongxia, et al. Battleplan acquisition cost forecast based on partial least squares regression[J]. Journal of Naval University of Engineering, 2005, 17(4): 65-66.

[18] 毛李帆, 姚建刚, 金永顺, 等. 中长期负荷预测的异常数据辨识与缺失数据处理[J]. 电网技术, 2010, 34(7): 148-150.

MAO Lifan, YAO Jiangang, JIN Yongshun, et al. Abnormal data identification and missing data filling in medium and long-term load forecasting[J]. Power System Technology, 2010, 34(7): 148-150.

(编辑  刘锦伟)

收稿日期：2014-07-08；修回日期：2014-09-27

基金项目(Foundation item)：教育部新世纪优秀人才支持计划项目(NCET-11-0977)；湖南省研究生科研创新项目(CX2013B369) (Project(NCET-11-0977) supported by the Program for New Century Excellent Talents in University; Project(CX2013B369) supported by the Postgraduate Innovative Research Project of Hunan Province)

通信作者：韦慧，博士研究生，从事路基路面养护工程研究；E-mail: 65234551@qq.com