文章编号：1004-0609(2010)S1-s0357-08
医用β-Ti30Nb13Zr0.5Fe合金的热变形行为
郭爱红，余 巍，张永强，朱雨生
(中国船舶工业集团公司，洛阳 471039)
摘 要：利用热模拟实验机对Ti30Nb13Zr0.5Fe(质量分数，%)医用钛合金在温度700～850 ℃、变形速率10-3～10 s-1范围内进行等温热压缩试验，观察变形后钛合金的显微组织，并根据动力学分析确定合金β相区热变形方程、应力指数n和激活能Q。结果表明： 温度变化不改变σ —ε曲线特征；应变速率对变形行为的影响较大，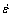
为1～10 s-1时，出现流变不稳定性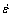；为10-2～1 s-1时，组织发生β相再结晶和动态回复；当θ＞800 ℃、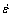＜10-2 s-1时，组织发生β相连续再结晶，导致晶粒粗化；合金β相区变形应力指数n和激活能Q分别为4.5和195 kJ/mol；综合考虑可热加工性和组织细化因素，温度为700～800 ℃、应变速率为10-3～10-1 s-1是良性热加工区域。
关键词：医用钛合金；热压缩；流动应力；显微组织；变形机制
中图分类号：TG 146 文献标志码：A
Hot deformation behaviors of biomedical β-Ti30Nb13Zr0.5Fe alloy
GUO Ai-hong, YUE Wei, ZHANG Yong-qiang, ZHU Yu-sheng
(Luoyang Ship Material Research Institute, Luoyang 471039, China)
Abstract: The hot deformation behaviors of Ti30Nb13Zr0.5Fe (mass fraction, %) alloy were studied by thermal-simulator in the temperature range of 700-850 ℃ and strain rate range of 10-3-10 s-1. The hot deformation equation, stress exponential n and deformation activation energy Q were established according to the dynamical analysis. The microstructures were observed by optical microscopy. The results indicate that the variation of deformation temperature doesn’t change the characteristics of true stress—strain curves, but the variation of strain rate has crucial effect on the deformation behaviors. The instable flow happens at strain rate of 1-10 s-1, the dynamic recrystallization and dynamic recovery of β phase occur at strain rate of 10-2-1 s-1. And the continual recrystallization and grain coarsening occur at strain rate less than 10-2 s-1 and temperature higher than 800 ℃. The stress exponential n and deformation activation energy Q of β phase are 4.5 and 195 kJ/mol, respectively. Considering workability and microstructure refining, the optimum conditions of hot deformation for Ti30Nb13Zr0.5Fe alloy are the temperature range of 700-800 ℃ and strain rate range of 10-3-10-1 s-1.
Key words: biomedical titanium alloy; heat deformation; flow stress; microstructure; deformation mechanism
纯钛和Ti-6Al-4V 合金由于比强度高、耐蚀性优异、生物相容性好而成为当代广泛应用的人工关节和齿根等硬组织植入和修复材料。然而，Ti-6Al-4V合金含对人体有毒元素V和Al，且该合金和纯钛弹性模量均高达100～110 GPa，是人体骨骼(10～40G Pa)的2～5倍，在人体内易于产生应力屏蔽效应，造成骨质吸收和植入体的松动[1]。添加无毒元素 Nb、 Mo、 Zr、 Ta、Sn等β型钛合金的弹性模量则更接近于人体骨骼的[2]。因此，开发由无毒、无过敏元素组成且具有良好力学和加工性能的低刚度β型钛合金成为当今医用钛合金的发展趋势[3-5]。目前，国内外开发的β型医用钛合金多含有熔点高、密度大β稳定元素Mo、 Nb、 Zr和Ta等，且熔炼困难，成本高。因此，在满足应用性能基础上降低成本和提高性价比成为发展新型医用钛合金亟待解决的问题。本研究小组采用廉价元素Fe来部分替代高价格、高熔点、大密度β稳定元素Nb，开发出Ti-30Nb-13Zr-0.5Fe亚稳定β型医用钛合金,该合金热加工后经简单热处理就可获得理想的组织和综合力学性能[6]，应用潜力巨大。
本文作者研究Ti-30Nb-13Zr-0.5Fe合金高温变形行为及组织演变规律，建立高温变形本构方程，确定了变形激活能Q，分析高温变形机制，为制定合理的热加工工艺提供理论依据和实验数据。
1 实验
1.1 实验材料
采用真空感应炉3次熔炼制备Ti-30Nb-13Zr- 0.5Fe(质量分数，%)合金5 kg铸锭。铸锭经1 100 ℃开坯，800～900 ℃自由锻造，β相区固溶处理，得到直径为22 mm的棒材，作为本试验原材料。合金锻棒相变点约为690 ℃，原始组织为等轴β相晶粒组织。
1.2 实验过程
利用Gleeble-2000型热模拟试验机进行等温热压缩实验。试样为d 8 mm×15 mm圆柱，上下端面加工0.2 mm润滑剂凹槽存储润滑剂，以减小试样端面与试验机压头之间的摩擦。试验温度为700、750、800、850 ℃，应变速率为10-3、10-2、10-1、1、10 s-1，变形量均为70%。试样变形后水淬以保留高温变形组织，升温、保温和整个压缩过程充氩气保护。
压缩后的试样沿轴向平均纵切，用OLYMPUS GX71型光学显微镜观察其组织，沿径向中间部位切取薄片制备TEM试样，用TECNAI G220型透射电镜观察位错组态。
2 结果与讨论
2.1 真应力—真应变曲线
图1所示为在700?850 ℃、10-3?10 s-1条件下合金变形的真应力—真应变曲线。由图1可知，应变速率相同、温度不同时，真应力—真应变关系曲线表现出相似的特征。在其他变形条件相同的情况下，流变应力随温度升高而降低，但降低幅度不大。这是因为试验所选的温度都处在β相区，变形主要由β相所控制，故应变速率相同、温度不同时，真应力—真应变曲线表现出相似的特征。而变形温度的升高则使热激活作用增强，位错产生滑移的临界分切应力减小。且随着温度的升高动态回复和动态再结晶也更容易进行，使位错密度下降，导致流变应力随温度升高而降低。但由于是在β相区变形，参与变形的滑移系数目基本相同，故流变应力随温度升高降低幅度不大。由图1还可以看出，在其他变形条件相同时，流变应力随应变速率的增加显著增大。这是因为，应变速率的增加使位错增殖率增大，加工硬化作用增强，故流变应力相应地增大。
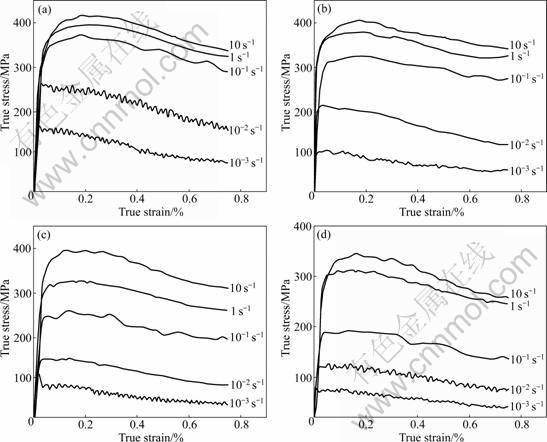
图1 在不同温度和应变速率下Ti-30Nb-13Zr-0.5Fe合金的真应力—真应变曲线
Fig.1 True stress—strain curves of Ti-30Nb-13Zr-0.5Fe alloy at different temperatures and strain rates: (a) 700 ℃; (b) 750 ℃; (c) 800 ℃; (d) 850 ℃
当应变速率大于1 s-1时，流变应力首先经历初始的加工硬化迅速达到峰值，然后随应变增加呈小许降低趋势。这是因为，高速大变形量变形后，外加载荷对试样做的功部分转化为热能。由于钛合金导热性较差，致使试样局部温度升高，流变应力下降。
当应变速率为10-1 s-1 时，流变应力随应变增加上升到峰值后进入流变“软化”阶段，真应力—真应变曲线出现较大的不连续的应力震荡峰。SESHACHARYULU等[7]认为，真应力—真应变曲线的应力震荡表明在此变形条件下，合金内部组织可能发生β相再结晶、α片层球化或出现裂纹。文献[8-10]中也指出，真应力—真应变曲线出现的应力震荡峰值是由于固溶元素原子与位错相互作用而产生的类似上、下屈服点现象。本研究温度均在β相区，变形组织全部是β相，排除了α片层球化的可能性；且变形后的金相组织中没有发现孔洞或裂纹，只有少量的再结晶组织。因此，10-1 s-1曲线呈现的不连续应力震荡应是固溶元素原子与位错相互作用和β相晶粒再结晶共同作用的结果。
当应变速率小于10-2 s-1时，真应力—真应变曲线呈锯齿状，处于较平稳状态，流变应力很低，且与变形量无关，变形产生的加工硬化与流变软化这两个因素相平衡。说明此时可能发生动态再结晶、动态回复或塑性变形。由于超塑性变形是通过细晶的β晶界面相对滑动引起，粗晶组织并不利于发生超塑性，排除超塑性变形的可能。而变形组织内除了新生的细小β相等轴晶粒外，还存在拉长的原始β晶粒，表明此时发生动态回复和动态再结晶。
图2所示为峰值应力(σm)随变形速率和温度变化曲线。由图2可以看出，在相同温度下，σm值随变形速率增加而增大，且根据变形速率大小可将σm分为3个区域，即高值(1～10 s-1)、中值(10-1 s-1)、低值(10-2～10-3 s-1)。在相同变形速率下，σm值随温度升高而下降，且变形速率越低，这一规律越不明显。若考虑钛合金在加工时的易流变性，应选择700 ℃以上，中低变形速率为宜。
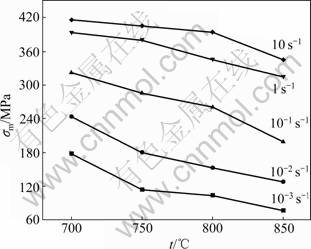
图2 最大流变应力值(σm)随变形速率的变化
Fig.2 Variation of maximum flow stress with strain rate at various temperatures
2.2 高温变形本构方程
根据热加工本构模型基础理论，高温变形过程中，材料在任何应变和稳态下的高温流变应力σ强烈依赖于变形温度T和应变速率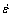。对不同材料热加工数据的研究表明，σ和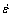之间的数学关系可用Arrhenius方程[11-15]表示：
低应力水平时：
ln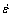=lnA1+n1lnσ (1)
高应力水平时：
ln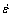=lnA2+βσ (2)
整个应力范围：
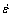=A[sinh(ασ)]nexp[-Q/(RT)] (3)
式中：A1、A2、A、n1、n、α、β为与温度无关的常数；A为结构因子；n为应力指数；α为应力水平参数；R为摩尔气体常数；T为变形绝对温度，K；Q为变形激活能，kJ/mol；σ为峰值应力，MPa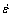；为应变速率，s-1。α、β和n之间满足关系式α=β/n。式(3)为一种包含Q和T的双曲正弦Arrhenius关系式，用于描述热激活稳态变形行为。
此外，Zener和Hollomon提出并验证应变速率和温度的关系可用一项参数Z表示：
Z=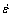exp[Q/(RT)] (4)
式中：Z为温度补偿变形速率因子；Q反映了材料热变形难易程度。Z和σ之间符合以下关系式：
Z=A[sinh(ασ)]n (5)
由式(5)可以得到：
sinh(ασ)=(Z/A1)/n (6)
根据双曲正弦函数的定义，有
sinh-1(ασ)=ln[ασ+(α2σ2+1)1/2] (7)
由此可将流变应力表达为含应变速率和温度的函数，也可表达为参数Z的函数：
σ=1/αln{(Z/A)1/n+[(Z/A)2/n+1]1/2} (8)
所以，只要已知A、Q(?H)、n和α等材料常数，即可求出材料在任意变形条件下的流变应力值。
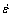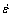根据式(1)和(2)，取流变应力为峰值应力，分别以lnσ和ln、σ和ln为坐标作图，用Origin软件线性回归，得式(3)。由式(1)和(2)知，n1可取图3(a)中4条直线斜率平均值6.7。β可取图3(b)中4条直线斜率平均值0.03。则α值为α=β/n1=0.004 5。
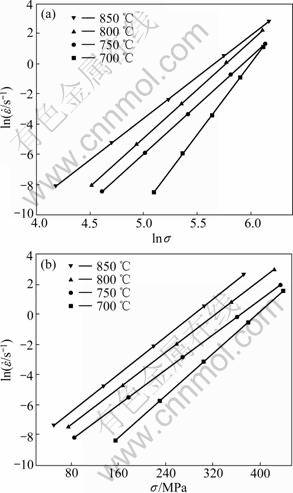
图3 合金峰值应力与应变速率间的关系
Fig.3 Relationship between flow stress (σ) and strain rate (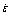
) of alloy at various temperatures
对式(3)两边取对数，并假定变形激活能与温度无关，可得
ln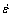=lnA-Q/RT+nln[sinh(ασ)]=A′+nln[sinh(ασ)] (9)
以ln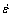和ln[sinh(ασ)]为坐标作图，用Origin线性回归得到图4(a)。该图表明流变应力和应变速率双曲正弦对数较好地满足了线性关系。
把式(4)代入式(5)，对其两边取对数得：
ln[sinh(ασ)]=A3+B×1 000/T (10)
以ln[sinh(ασ)]和1/T为坐标作图，得图4(b)。由该图知σ与T较好的符合式(10)线性关系，证明变形时σ与T之间关系属于Arrhenius关系，可用Z参数描述变形时的流变应力行为。对式(3)求偏导得
Q=R{?ln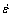/?ln[sinh(ασ)]}T×{?ln[sinh(ασ)]/?(1/T)} 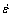(11)
式中：大括号内的两项分别为一定温度下ln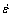—ln[sinh(ασ)]关系和应变速率一定条件下ln[sinh(ασ)]—1/T关系斜率。图4(a)和(b)直线的斜率平均值4.6×10-3和5.1×10-3，代入式(11)求得变形激活能Q值为195 kJ/mol，接近于β相自扩散激活能153 kJ/mol[16]，说明在700～850 ℃，合金热变形主要受β相扩散控制。
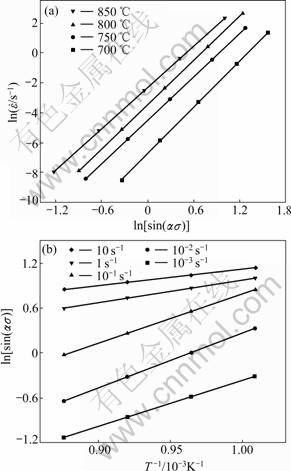
图4 峰值应力与应变速率和温度的线性关系
Fig.4 Peak flow stress dependence on (a) strain rate and (b) temperature
对式(5)两边求对数得
lnZ=lnA+nln[sinh(ασ)] (12)
将Q值和变形条件代入式(4)后求Z值，以ln[sinh(ασ)]和lnZ为坐标作图，线性回归得图5，图中直线斜率即为n值，n=4.55，A=342 s-1。图5表明ln[sinh(ασ)]和lnZ在实验参数范围内线性关系吻合很好，说明此时变形的σ、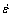和T之间关系可用(3)式描述。
通过以上计算，得到Ti-30Nb-13Zr-0.5Fe合金材料常数，变形激活能Q=195 kJ/mol，应力指数n=4.5，应力水平参数α=0.004 5 mm2/N，结构因子A= 342/s。
将A、Q、n、α等参数代入式(3)，得合金700?850 ℃变形本构方程为
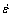=342[sinh(0.004 5σ)]4.5exp(-195/RT) (13)
将上述材料常数代入式(8)，可得由参数Z表示的塑性流变应力方程：
σ=222ln{(Z/342)1/4.5+[(Z/342)2/4.5+1]1/2} (14)
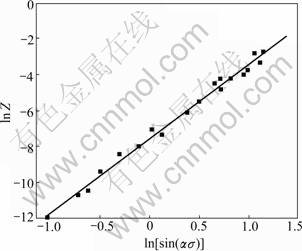
图5 流变应力与Z参数的关系曲线
Fig.5 Relationship between flow stress and Zener-Hollomon parameter
2.3 热变形组织
图6 所示为Ti-30Nb-13Zr-0.5Fe合金在应变速率为10-2 s-1不同温度变形后的金相组织。由图6可以看出，经700 ℃和750 ℃变形时，沿拉长的原始β晶界生成细小的等轴再结晶晶粒，且随变形温度升高，再结晶晶粒增多，合金在变形过程中发生不完全再结晶；经800 ℃变形时，变形组织完全由等轴再结晶晶粒组成，平均晶粒尺寸约为25 μm，合金变形过程中发生完全再结晶；而经850 ℃变形时，再结晶晶粒长大，且晶界呈锯齿状，发生连续再结晶(见图6(d))。这是因为在高温和低应变速率变形条件下，再结晶形核和长大的驱动力大，容易发生再结晶和晶粒长大，在随后的变形过程中，再结晶晶粒会再次承受变形[17]，使晶界呈锯齿状。
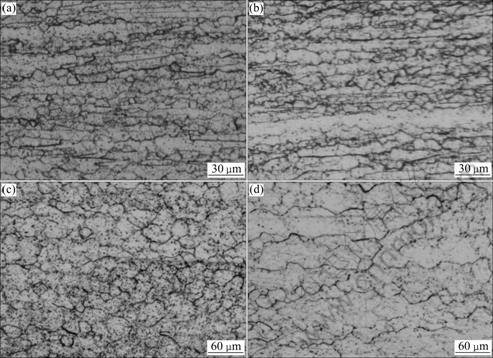
图6 应变速率为10-3 s-1时变形后钛合金的显微组织
Fig.6 Microstructures of Ti alloys after hot deformation at strain rate of 10-3 s-1 and various temperatures: (a) 700 ℃; (b) 750 ℃; (c) 800 ℃; (d) 850 ℃
图7所示为合金800 ℃不同应变速率变形后的金相组织。由图7可以看出，当应变速率为10 s-1时，出现局部塑性流动现象(见图7(a))；当应变速率减小至10-1 s-1时，局部塑性流动现象减弱，高倍下可看到在大变形量区域β晶界呈弯曲状，且沿弯曲晶界布满晶粒尺寸约为2～3 μm的再结晶晶粒(见图7(b))。说明在此变形条件下，合金变形过程由动态回复和动态再结晶共同控制。当应变速率减小至10-2 s-1，变形组织完全由晶粒尺寸约为20 μm左右的再结晶晶粒组成，发生完全再结晶(见图7(c))。由上述分析可知，合金变形组织与真应力－真应变曲线所反映的结果是一致的。从组织细化和易流变性因素综合考虑，700～800 ℃、10-3～10-2 s-1为合金良性热加工参数范围。
图7 经800 ℃不同变形速率变形后的微观组织
Fig.7 Microstructures of alloys after hot deformation at 800 ℃ and various strain rates: (a) 10 s-1; (b) 10-1 s-1; (c) 10-3 s-1
2.4 热变形机制
图8所示为不同变形条件变形后合金内位错组态的TEM像。由图8可看出，较低温度(700 ℃)变形时，出现弯曲位错线(见图8(a))，表明位错通过攀移和交滑移实现动态回复是这一阶段的主要变形机制。此外，低温变形时加工硬化作用较强， 导致大量位错缠结，位错线短小。相同应变速率下变形温度升高至850 ℃ (见图8(b))，位错线变得长而平直，且平行排列，位错密度很低，表明位错滑移是这一阶段的主要变形机制。随着变形温度升高，位错产生滑移的临界分切应力减小，动态回复更容易进行，位错密度下降。这与真应力—真应变曲线所反映的结果是一致的。当850 ℃变形、增大应变速率至10-1 s-1时，位错密度增加，又出现很多交叉滑移带(见图8(c))，说明此时位错的滑移和交滑移为主要变形机制。这是因为应变速率的增加使位错增殖率增大，加工硬化作用增强。这与真应力－真应变曲线所反映的结果是吻合的。
图8 不同变形条件变形后位错组态的TEM像
Fig.8 TEM images of alloys after deformation under different conditions: (a) 700 ℃, 10-3 s-1; (b) 850 ℃, 10-3 s-1; (c) 850 ℃, 10-1 s-1
3 结论
1) Ti-30Nb-13Zr-0.5Fe合金在β相区变形时，相同应变速率下的应力—应变曲线特征大致相似，接近稳态流动型。流动应力随应变速率升高和温度降低而增加，且流动应力对前者的敏感性要大于后者。
2) β相区变形时，流变应力本构关系满足双曲正弦模型，也可以用包含Arrhenius 项的Z参数描述其流变行为，计算所得方程如下:
=342[sinh(0.004 5σ)]4.5exp(-195/RT)
σ=222ln{(Z/342)1/4.5+[(Z/342)2/4.5+1]1/2}
3) 当温度为700～800 ℃，应变速率为10～1 s-1时，出现局部塑性流动；应变速率为10-3～10-1 s-1时，发生动态回复和动态再结晶。温度高于800 ℃、应变速率低于10-2 s-1时，发生连续再结晶，使晶粒粗化。综合考虑可热加工性和组织细化因素，以700～800 ℃，10-3～10-1 s-1热加工参数范围为佳。
4) 在低温和高应变速率下，合金变形机制为位错通过攀移和交滑移实现动态回复；在高温和低应变速率下，合金变形机制为位错滑移。
REFERENCES
[1] NIINOMI M. Fatigue performance and cyto-toxicity of low rigidity titanium alloy, Ti-29Nb-13Ta-4.6Zr [J]. Biomaterials, 2003, 24: 2673-2683.
[2] EISENBARTH E, VELTEN D. Biocompatibility of beta- stabilizing elements of titanium alloys [J]. Biomaterials, 2004, 25: 5705-5713.
[3] NIINOMI M. Recent metallic materials for biomedical applications [J]. Metal Mater Trans A, 2002, 33A: 477-486.
[4] NIINOMI M. Mechanical properties of biomedical titanium alloys [J]. Materials Science and Engineering A, 1998, 243: 31-236.
[5] 周 宇, 杨贤金, 崔振铎. 新型医用β-钛合金的研究现状及发展趋势[J]. 金属热处理, 2005, 30(1): 47-50.
ZHOU Yu, YANG Xian-jin, CUI Zhen-duo. Present status and developmental trend of novel β-titanium alloys for biomedical applications [J]. Heat Treatment of Metals, 2005, 30(1): 47-50.
[6] 郭爱红, 崔文芳, 周 廉. 新型医用TiNbZrFe合金的组织和力学性能[J]. 材料与冶金学报, 2008, 7(4): 288-292.
GUO Ai-hong, CUI Wen-fang, ZHOU Lian. Microstructures and mechanical properties of meta-stable β type TiNbZrFe alloys for biomedical application [J]. Journal of Materials and Metallurgy, 2008, 7(4): 288-292.
[7] SESHACHARYULU T, MEDEIROS S C, FRAZIER W G. Hot working of commercial Ti-6Al-4V with an equiaxed α-β microstructure: materials modeling considerations [J]. Mater Sci and Eng A, 2000, A284: 184-194.
[8] 彭益群. 热变形参数对Ti-10V-2Fe-3Al 合金组织与流变应力的影响研究[D]. 北京: 北京航空航天大学, 1989: 50-52.
PENG Yi-qun. Research on the effects of hot deformation parameters on microstructures and flow stress of Ti-10V-2Fe-3Al alloy [D]. Beijing: Beijing Space and Aeronautic University, 1989: 50-52.
[9] MONTHEILLET F, DAJNO D. Hot deformation of the high strength beta-cez titanium alloy titanium’92 science and technology [C]// FROES F H, CAPLAN I L, et al. San Diego: The Minerals, Metals & Materials Society, 1993: 1347-1349.
[10] 叶文君, 脱祥明, 王世洪. β21S 钛合金热压缩变形行为[J]. 稀有金属, 2002, 26(1): 23-27.
YE Wen-jun, TUO Xiang-ming, WANG Shi-hong. Hot press deformation behavior of β21S titanium alloy [J]. Rare Metals, 2002, 26(1): 23-27.
[11] 舒 滢, 曾卫东, 周 军. BT20合金高温变形行为的研究[J]. 材料科学与工艺, 2005, 13(1): 55-58.
SHU Ying, ZENG Wei-dong, ZHOU Jun. High temperature deformation behavior of BT20 alloy [J]. Materials Science and Technologies, 2005,13(1): 55-58.
[12] 洪 权, 张振棋. Ti-6Al-2Zr-lMo-lV合金的热变形行为[J]. 航空材料学报, 2001, 21(1): 10-12.
HONG Quan, ZHANG Zhen-qi. Hot deformation behavior of Ti-6Al-2Zr-lMo-lV alloy [J]. Journal of Aeronautic Materials, 2001, 21(1): 10-12.
[13] POIRIER J P. 晶体的高温塑性变形[M]. 大连: 大连理工大学出版社, 1989: 1-20.
POIRIER J P. Hot plastic deformation of crystal [M]. Dalian: University of Dalian Science and Technology Press, 1989: 1-20.
[14] 沈 健. 热压缩2091Al-Li合金的流变应力行为[J]. 稀有金属, 1998, 22(1): 47-50.
SHEN Jian. Flow stress behavior of hot pressed 2091Al-Li alloy [J]. Rare Metals, 1998, 22(1): 47-50.
[15] SHEPPARD T, PARSON N C, ZAIDI M A. Dynamic recrystallization in Al-Mg [J]. Met Sci, 1983, 17(10): 481-487.
[16] SESHACHARYULU T, MEDEIROS SC, MORGAN J T. Hot deformation mechanism in ELI grand Ti-6Al-4V [J]. Scripta Materialia, 1999, 41(3): 283-288.
[17] 曾卫东, 周义刚, 舒 滢. 基于加工图的Ti-40阻燃钛合金热变形机理研究[J]. 稀有金属材料与工程, 2007, 36(1): 1-6.
ZENG Wei-dong, ZHOU Yi-gang, SHU Ying. A study of hot deformation mechanisms in Ti-40 burn resistant titanium alloy using processing maps [J]. Rare Metal Materials And Engineering, 2007, 36(1): 1-6.
(编辑 李艳红)
通信作者：郭爱红; 电话: 0379-67256039; E-mail: aihonggg@sina.com.cn
