IMI834钛合金在热拉伸变形过程的流变行为建模
来源期刊:中国有色金属学报(英文版)2015年第3期
论文作者:M. H. GHAVAM M. MORAKABATI S. M. ABBASI H. BADRI
文章页码:748 - 758
关键词:钛合金;流变行为;热拉伸变形;本构方程
Key words:titanium alloy; flow behavior; hot tensile deformation; constitutive model
摘 要:建立合适的本构模型预测IMI834钛合金在α+β区的热拉伸流变行为。热拉伸实验在温度为800~1025 °C、应变速率为0.001~0.1 s-1条件下进行。此本构模型通过Arrhenius型方程来表征应变为0.08~0.22时合金的热拉伸行为。结果表明,在不同应变条件下IMI834钛合金的热拉伸变形激活能范围为519~557 kJ/mol。利用标准统计参数估算预测合金流变应力曲线的精度。所预测的合金的流变应力曲线与实验结果十分吻合。
Abstract: A proper constitutive model was developed to predict the hot tensile flow behavior of IMI834 titanium alloy in α+β region. Hot tensile tests were performed at 800-1025 °C and 0.001-0.1 s-1. The constitutive model was developed through an Arrhenius-type equation at strains of 0.08-0.22 to characterize the hot tension behavior. It was found that the activation energies for hot tensile deformation of IMI834 titanium alloy are in the range of 519-557 kJ/mol at different strain values. The accuracy of predicted flow stress curves was evaluated using standard statistical parameters. These curves are appropriately found to be in good agreement with the experimental ones.
Trans. Nonferrous Met. Soc. China 25(2015) 748-758
M. H. GHAVAM, M. MORAKABATI, S. M. ABBASI, H. BADRI
Metallic Materials Research Center, Maleke Ashtar University of Technology, Tehran 009821, Iran
Received 10 March 2014; accepted 9 July 2014
Abstract: A proper constitutive model was developed to predict the hot tensile flow behavior of IMI834 titanium alloy in α+β region. Hot tensile tests were performed at 800-1025 °C and 0.001-0.1 s-1. The constitutive model was developed through an Arrhenius-type equation at strains of 0.08-0.22 to characterize the hot tension behavior. It was found that the activation energies for hot tensile deformation of IMI834 titanium alloy are in the range of 519-557 kJ/mol at different strain values. The accuracy of predicted flow stress curves was evaluated using standard statistical parameters. These curves are appropriately found to be in good agreement with the experimental ones.
Key words: titanium alloy; flow behavior; hot tensile deformation; constitutive model
1 Introduction
IMI834 titanium alloy has been the most recently developed near-alpha type titanium alloy. High ultimate tensile strength at room temperature, i.e., 1030 MPa, operating temperatures up to 600 °C, and good combination of creep and fatigue resistance at elevated temperatures promoted its application in discs and blades in the high pressure part of compressors and advanced jet engines [1-3]. Titanium alloy components are more difficult to be fabricated than other traditional metallic materials due to their poor formability at room temperature, high flow stress at elevated temperatures, and high sensitivity of flow stress to temperature [4]. Thermomechanical processing (TMP) is an effective method for forming and improving microstructure and mechanical properties of titanium components. Thermomechanical processing of these alloys involves primary β processing (ingot breakdown) stage, for conversion of a cast ingot to a worked billet, and secondary α+β processing for preparing the final product [5-7].
The constitutive models provide a great potential to describe the change in mechanical properties under an external loading. Various analytical, phenomenological, and empirical constitutive models have been developed to predict the high temperature behavior of the metallic materials [8-11]. Among these models, the phenomenological models less strictly relate to the physical theories and have been extensively employed in flow behavior modeling of the metallic materials. In addition, only a reasonable number of material constants are needed in this type of models, which can be acquired through a regression analysis of a limited amount of experimental results [12-16]. A phenomenological model initially proposed by JONAS et al [13] based on an Arrhenius-type equation has been hailed by most of researchers to predict the high temperature flow stress of materials. Phenomenological models have been developed for the prediction of hot compression flow behavior of Ti-6Al-4V [17-19], Ti-6Al-7Nb [20], Ti17 [21], Ti60 [22,23] and IMI834 alloys [24-26] and also hot tension flow behavior of Ti-6Al-4V alloy [27-29]. VANDERHASTEN et al [27] explored the tensile behavior at the strain rates ranging from 5×10-4 to 5×10-2 s-1 and various temperatures up to 1050 °C, and utilized the modified Norton-Huff law to characterize the tensile behavior of Ti-6Al-4V alloy in domains based on the temperature-strain rate combinations. For each domain, the Norton-Hoff parameters have been determined and the equation has a high precision. XIAO et al [28] utilized hyperbolic-sine Arrhenius-type equation to predict the tensile behavior of Ti-6Al-4V alloy at temperatures ranging from 650 to 750 °C and strain rates between 5×10-4 and 5×10-2 s-1 up to a strain of 0.22. They reported that the predicted flow stress curves by Arrhenius-type equations were appropriately found to be in good agreement with the experimental ones.
Considering that failures arise mainly from tensile stresses, it is necessary to find out the response of this alloy to these stresses. Although the constitutive model for IMI834 alloy has been developed using the Arrhenius-type equation via hot compression tests [24-26], no such model has been developed yet for IMI834 alloy based on uniaxial tensile test. Therefore, flow behavior modeling of IMI834 during hot tensile deformation at different elevated temperatures is the subject of the current study.
2 Experimental
An IMI834 ingot was cast using a vacuum arc remelting (VAR) furnace. The chemical composition of this alloy is listed in Table 1. The transformation temperature of the alloy was 1050 °C. It was subsequently homogenized at 1150 °C for 5 h in the single-phase β zone to reduce the segregation. Then, the ingot was hot-rolled at 1150 °C to a reduction in thickness of 60% and then was water-quenched. Flat tensile test specimens were prepared from the hot-rolled plate along rolling direction with a gauge section of 3 mm×6 mm×25 mm according to ASTM-E8 standard. Hot tensile tests were performed in an Instron 8502 testing machine equipped with a resistance furnace. The specimens were deformed at temperatures of 800, 900, 1000 and 1025 °C and strain rates of 0.001, 0.01 and 0.1 s-1. In order to obtain thermal homogenization, specimens were held at deformation temperatures prior to the test for 10 min, and were water-quenched immediately after the deformation. Microstructural studies were performed by optical microscopy. Specimens were polished mechanically and then etched in 60% H2O2+10% HF+30% H2O solution. The micro- structure of the as-rolled material consists of fully β transformed by Widmanstatten morphology and shown in Fig. 1. However, due to different orientations, Widmanstaten morphology is not visible in some grains.
Table 1 Chemical composition of IMI834 alloy (mass fraction, %)


Fig. 1 Microstructure of as-rolled IMI834 alloy
The average of grain size is 348 μm, although recrystallized grains and elongated grains on the order of 100 and 800 μm, respectively, can be observed.
3 Results and discussion
3.1 Flow stress behavior
Typical true stress-true strain curves for IMI834 alloy obtained at 800, 900, 1000 and 1025 °C and strain rates of 0.001-0.1 s-1 are presented in Fig. 2. The general characteristics of the flow curves are significantly affected by the temperature and strain rate. Four types of flow curves can be distinguished in Fig. 2. The first group encompasses the curves obtained at low two-phase α+β zone temperatures (800 and 900 °C) and at high strain rate (0.1 s-1), which depict a significant work hardening region up to ultimate tensile strength (UTS) followed by a short post-UTS region. The second category consists of flow curves produced at the same temperatures and lower strain rates (0.001-0.01 s-1). Under this condition, work hardening is smaller than that of the first category of curves; but it is significantly consistent. Moreover, strain at failure increases considerably in comparison with the first category of flow curves. The third category encompasses the curves obtained at the upper two-phase α+β zone temperatures (1000 and 1025 °C) and high strain rate (0.1 s-1), which exhibit a peak stress, followed by a region down to the steady state, suggesting a typical dynamic recrystallization accompanied plastic flow process. The fourth category consists of curves obtained at the same temperatures and low strain rates (0.001-0.01 s-1). Under this condition, work hardening region is negligible and the flow curves show a steady state behavior with a low rate stress drop beyond the necking. Significant work hardening seen in the first category of flow curves is related to the high volume fraction of high-strength α phase. It is reported that α phase holds high strength at temperatures below the transformation temperature and form unstable shear bands at high strain rates which are easily converted into cracks [30]. SEMIATIN et al [31] reported that the strain rate and test temperature have a marked influence on the workability of titanium alloys. Specifically, a sharp transition from semi-brittle behavior due to intergranular failure at high strain rates and low temperatures to very ductile behavior at low strain rates and high temperatures was observed in their work. The transition from brittle to ductile behavior occurs at a critical stress value. This critical stress for Ti-6Al-2Sn- 4Zr-2Mo has been reported to be about 250 MPa [32,33]. In the second category, at low deformation temperatures, transition from semi-brittle behavior to very ductile behavior occurred with decreasing the strain rate, so the strain to failure increased. The studies conducted by WANJARA et al [7, 24] and VO et al [25, 34] on hot compression behavior of IMI834 alloy and by VANDERHASTEN et al [27, 35], on hot tension of Ti-6Al-4V exhibited work hardening in the lower two-phase α+β zone which is related to the generation, pile-up and interaction of dislocation. In addition, in the upper two-phase α+β zone, the steady state flow behavior is reportedly seen and attributed to a balance between dynamic restoration phenomena and work hardening.

Fig. 2 True stress-true strain curves of IMI834 titanium alloy obtained by uniaxial tensile test at different strains rates

Fig. 3 Microstructures of IMI834 alloy deformed at 800 °C and 0.1 s-1 (a), 1000 °C and 0.1 s-1 (b), 800 °C, 0.001 s-1 and 20% of failure strain (c), 800 °C, 0.001 s-1 and failure strain (d) and 1000 °C and 0.001 s-1 (e)
Figure 3 illustrates the microstructure observed near the fracture zone of the specimens tested under different deformation conditions. As seen, at 800 °C and 0.1 s-1 (Fig. 3(a)), hot tension leads to the formation of grain boundary cracks. The microstructures contain high volume fraction of high-strength α phase. As the deformation temperature is low, thermally activated processes do not accompany grain boundary sliding (GBS). Therefore, grain boundary cracks appear in α matrix under these conditions. The microstructure after deformation at 1000 °C and 0.1 s-1 is shown in Fig. 3(b). Under this condition, dynamic restoration phenomena (dynamic recovery and dynamic recrystallization) lead to an increase in strain to failure. Dynamic recrystallized grains are also shown in Fig. 3. However, because of high volume fraction of BCC structure β phase (50% approximately), dynamic recovery exposed by serrations in grain boundary is the other restoration phenomenon under this condition. In other words, with the increase in strain, the serration of grain boundaries becomes more intensified and a small amount of recrystallized grains are observed in the vicinity of prior-grain boundaries [36]. Figures 3(c) and (d) illustrate the microstructure observed at 800 °C and 0.001 s-1 near the fracture zone (20% of the strain to failure) and fracture zone (strain to failure), respectively. Under this condition, deformation does not lead to brittle fracture. At low strain (20% of strain to failure, Fig. 3(c)) microvoids form, and at failure strain (Fig. 3(d)) coalescence of them lead to fracture. Similar behavior was reported for hot ductility of ferritic stainless steel by MINTZ et al [37] who suggested that, with a decline in the stress acting on the boundary, the amount of grain boundary sliding reduces. Cavity formation during hot tension of Ti-6Al-4V alloy at 550-955 °C (single α phase temperature region to tβ-50 °C in α+β phase temperature region) was also reported by SEMIATIN et al [38]. Figure 3(e) illustrates the microstructure of the IMI834 alloy after deformation at 1000 °C and 0.001 s-1. Under this condition, sufficient time is available for dynamic recovery to occur and dynamic recrystallization is restricted. Dynamic recovery as the serration of grain boundaries is dominant over the whole microstructure. Notwithstanding the absence of dynamic recrystallization, elongation increases in comparison with that at higher strain rates. This can be attributed to a decrease in dislocation density due to the decrease of strain rate in transgranular ductile fracture [37].
The hot ductility curves of elongation-to-fracture against the test temperature of IMI834 alloy are shown in Fig. 4. As seen, at all strain rates, elongation increases with increasing the test temperature. Also, elongation increases with decreasing the strain rate at all temperatures. Deformation of IMI834 alloy has a similar behavior to those alloys with high stacking fault energy, demonstrating serrated grain boundaries at high temperatures and transgranular fracture due to coalescence of microvoids at low strain rate. MINTZ et al [37] reported that when ferrite forms from austenite under strain, the onset of dynamic recrystallization at austenite boundaries results in serrated boundaries which are reflected in the subsequent ferrite boundaries, and this would be expected to prevent grain boundary sliding from occurring. So, failure is mainly transgranular with only a very small amount of grain boundary sliding and microvoid coalescence is therefore the major mode of failure. For transgranular ductile fracture, increasing the strain rate by increasing the dislocation density would be expected to reduce ductility. It is clear from Fig. 5 that increasing strain rate increases the peak stress markedly. Increasing the strain rate prevents the restoration from occurring, and it is only at the higher temperatures (1000 and 1025 °C) that strain rate has little influence on strength.

Fig. 4 Variation of elongation of IMI834 alloy with test temperature at different strain rates

Fig. 5 Variation of peak stress of IMI834 alloy with test temperature at different strain rates
3.2 Constitutive equations and material constants
The Arrhenius equation is widely used to describe the relationship among the strain rate, flow stress and temperature, especially at high temperatures. Also, the effects of temperature and strain rate on the deformation behavior of materials can be represented by Zenner- Holloman parameter, Z, in an exponent-type equation. These are represented in mathematical forms in Eqs. (1)-(5). For lower stress level (ασ<0.8) and higher stress level (ασ>1.2), Eqs. (3) and (4) can be used, and for all stress levels Eq. (5) can be used, respectively [39]:
 (1)
(1)
 (2)
(2)
 for
for  <0.8 (3)
<0.8 (3)
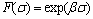 for
for  >1.2 (4)
>1.2 (4)
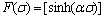 for all
for all  (5)
(5)
where Q is the activation energy (kJ/mol); R is the universal gas constant (8.314 J/(mol·K)); T is the absolute temperature in K; A, β, n1, α and n are the material constants. The value of α is calculated through
 (6)
(6)
Flow stress data obtained from the hot tension tests under various deformation conditions were employed to investigate the material constants of the constitutive equations. It is widely accepted that the effect of strain on flow stress will not be considered in Eqs. (1) and (2). However, the effect of strain on flow stress of IMI834 alloy at elevated temperature is significant. In the present work, the effects of strain on the material constants of constitutive equations were studied. The strain of 0.1 is taken as an example to introduce the solution procedures to calculate the material constants. For lower stress level (ασ<0.8) and higher level stress (ασ>1.2), substituting the power low (Eq. (3)) and exponential law (Eq. (4)) of F(σ) into Eq. (2) gives
 (7)
(7)
 (8)
(8)
where B and 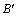 are the material constants, depending on the deformation temperatures.
are the material constants, depending on the deformation temperatures.
Taking the logarithm of both sides of Eqs. (7) and (8), respectively, gives
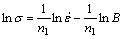 (9)
(9)
 (10)
(10)
Substituting the values of the strain rates and corresponding flow stresses (for true strain of 0.1) into Eqs. (9) and (10) gives the relationship between the flow stress and strain rate, as shown in Fig. 6. The values of n1 and β can be acquired from the slope of the parallel and straight lines in the  plots, respectively. The mean values of n1 and β are calculated to be 4.15 and 0.037 MPa-1, respectively. The value of α is calculated from Eq. (6) to be 0.009 MPa-1. The value of α is in good agreement with previous reported values for Ti alloys in α+β region represented in Table 2.
plots, respectively. The mean values of n1 and β are calculated to be 4.15 and 0.037 MPa-1, respectively. The value of α is calculated from Eq. (6) to be 0.009 MPa-1. The value of α is in good agreement with previous reported values for Ti alloys in α+β region represented in Table 2.
For all the stress levels, substituting Eq. (5) into Eq. (2) yields
 (11)
(11)
Taking the logarithms of both sides of Eq. (11) yields
 (12)
(12)
The values of n can be derived from the slopes of ln[sinh(ασ)]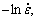 as shown in Fig. 7(a). The values of n are calculated by averaging the values of n derived at different deformation temperatures. From a group of parallel and straight lines in Fig. 7(a), the value of n for α+β region can be easily evaluated to be 2.76. For a particular strain rate, differentiation of Eq. (12) lends to
as shown in Fig. 7(a). The values of n are calculated by averaging the values of n derived at different deformation temperatures. From a group of parallel and straight lines in Fig. 7(a), the value of n for α+β region can be easily evaluated to be 2.76. For a particular strain rate, differentiation of Eq. (12) lends to
 (13)
(13)
The values of Q can be obtained from the slopes in the plot of ln[sinh(ασ)]-(1/T), as illustrated in Fig. 7(b). The values of Q can be determined by averaging the values of Q under different strain rates. The values of  at a particular strain can be derived from the interception of ln[sinh(ασ)]-
at a particular strain can be derived from the interception of ln[sinh(ασ)]- At a true strain of 0.1, the Q value is found to be 521 kJ/mol for α+β region. Similarly, the activation energy in the strain range of 0.08-0.22 is obtained to be in the range of 519-557 kJ/mol for different strain values in α+β region. The activation energy is well higher than that of self-diffusion in α (150 kJ/mol) or β (153 kJ/mol) phase, which is consistent with the results of previous researches in titanium alloys (according to Table 2). Several researchers tried to explain the high activation energy in terms of occurrence of dynamic recrystallization [43-45]. Considering the microstructural observation displayed in Fig. 3, limited dynamic recrystallization (only at 1000 °C and 0.1 s-1) occurred. Therefore, the high activation energy for hot tension of IMI834 alloy can be related to the flow stress values of the hard α phase and soft β phase, as well as to the temperature dependency of the volume fraction of the harder phase, i.e., α phase in titanium alloys. WANJARA et al [24] also believed that high activation energy for α+β deformation is influenced by the difference in the strength of α and β phases.
At a true strain of 0.1, the Q value is found to be 521 kJ/mol for α+β region. Similarly, the activation energy in the strain range of 0.08-0.22 is obtained to be in the range of 519-557 kJ/mol for different strain values in α+β region. The activation energy is well higher than that of self-diffusion in α (150 kJ/mol) or β (153 kJ/mol) phase, which is consistent with the results of previous researches in titanium alloys (according to Table 2). Several researchers tried to explain the high activation energy in terms of occurrence of dynamic recrystallization [43-45]. Considering the microstructural observation displayed in Fig. 3, limited dynamic recrystallization (only at 1000 °C and 0.1 s-1) occurred. Therefore, the high activation energy for hot tension of IMI834 alloy can be related to the flow stress values of the hard α phase and soft β phase, as well as to the temperature dependency of the volume fraction of the harder phase, i.e., α phase in titanium alloys. WANJARA et al [24] also believed that high activation energy for α+β deformation is influenced by the difference in the strength of α and β phases.

Fig. 6 Relationship between ln σ and ln ε (a), σ and  (b)
(b)

Fig. 7 Relationship between ln[sinh(ασ)] and  (a), and ln[sinh(ασ)] and T-1 (b) for IMI834 alloy
(a), and ln[sinh(ασ)] and T-1 (b) for IMI834 alloy
Table 2 Obtained parameters α and Q values for different titanium alloys

It is usually assumed that the influence of strain on flow stress at evaluated temperatures is insignificant and thereby would not be considered in Eq. (1). However, the effect of strain on the material constants is significant in the entire strain range. Therefore, compensation of strain should be taken into account in order to derive constitutive equations to predict the flow stress more accurately. The influence of strain in the constitutive equation is incorporated by assuming that the activation energy (Q) and material constants (n1, β, α, n and ln A) are polynomial function of strain. In the present work, the values of the material constants were evaluated in the strain range of 0.08-0.22 with an interval of 0.02, the corresponding curves are shown in Fig. 8. These values are then employed to fit the polynomial function. A sixth order polynomial, as shown in Eq. (14), is found to represent the influence of strain on material constants with a very valid correlation and generalization. Due to flow instabilities of hot tension process, constitutive equation is not able to predict the flow stress at strains lower than 0.08 and higher than 0.22. At strains lower than 0.08, flow stress increases significantly at lower temperatures, whereas at higher temperatures, work hardening regime is not seen, and flow stress decreases with the increase of strain. At strains higher than 0.22, the specimen deformed at 800 °C and 0.1 s-1 is fractured and under this condition data are not available.

Fig. 8 Variation of constants IMI834 n1 (a), β (b), α (c), n (d), Q (e) and ln A (f) with true strain
n1=533991x6-538771x5+227592x4-51238x3+6464.2x2-431.24x+15.964
β=46696x6-42651x5+16122x4-3235.4x3+365.13x2-22.046x+0.5931
α=9120.6x6-8226.1x5+3062.3x4-604.15x3+66.997x2-3.9815x+0.1081
n=651831x6-625113x5+249626x4-53067x3+6336x2-402.39x+13.345
Q=216x6-216x5+642x4-107x3+106x2-89702x+2800.4
ln A=107x6-107x5+530x4-106x3+121766x2-7545.3x+241.3 (14)
Once the material constants are evaluated, the flow stress at a particular strain can be predicted. The flow stress can be written as a function of parameter Z, considering the definition of the hyperbolic law and Eqs. (1) and (11):
 (15)
(15)
3.3 Verification of constitutive equation
The developed constitutive equations for IMI834 alloy in α+β region, were verified against experimental results. Applying the determined material constants of the constitutive equation, the flow stress value was calculated under different deformation conditions. Figure 9 shows the comparison of experimental stress-strain data with the calculated values. It can be easily found that the proposed deformation constitutive equation gives an accurate and precise estimate of the flow stress for IMI834 alloy.

Fig. 9 Comparison between predicted (dots) and measured flow stress curves (solid line) of IMI834 alloy at different strain rates
The predictability of the developed constitutive equation considering the compensation of strain could be quantified in terms of standard statistical parameters such as correlation coefficient (R) and average absolute error (AARE). These are expressed by [46]
 (16)
(16)
 (17)
(17)
where E is the experimental flow stress and P is the predicted flow stress obtained from the developed constitutive equation;  and
and  are the mean values of E and P, respectively; N is the total number of data used in this study; R is a commonly used statistical parameter and provides information on the strength of the linear relationship between the experimental and predicted data. Sometimes, higher value of R may not necessarily indicate a better performance in which the tendency of the equation could be biased towards higher or lower values [47]. The AARE is calculated through a term by comparison of the relative error and therefore is an unbiased statistical parameter for determining the predictability of the equation [46]. As can be seen from Fig. 10, the values of R and AARE are 0.994408 and 7.4646%, respectively. The obtained results for different hot tension conditions are presented in Table 3. This indicates that the proposed constitutive equation gives an accurate and precise estimate of the flow stress.
are the mean values of E and P, respectively; N is the total number of data used in this study; R is a commonly used statistical parameter and provides information on the strength of the linear relationship between the experimental and predicted data. Sometimes, higher value of R may not necessarily indicate a better performance in which the tendency of the equation could be biased towards higher or lower values [47]. The AARE is calculated through a term by comparison of the relative error and therefore is an unbiased statistical parameter for determining the predictability of the equation [46]. As can be seen from Fig. 10, the values of R and AARE are 0.994408 and 7.4646%, respectively. The obtained results for different hot tension conditions are presented in Table 3. This indicates that the proposed constitutive equation gives an accurate and precise estimate of the flow stress.

Fig. 10 Correlation between experimental and predicted flow stress data from constitutive equation
Table 3 AARE and R values of IMI834 alloys under different hot working conditions

Moreover, it is of great interest to evaluate the capability of the proposed constitutive model to predict the flow stress behavior of IMI834 alloy under the conditions of which the data are not incorporated in the model. In this regard, the flow stress as a function of strain, temperature and strain rate has been simulated under different conditions, the results of which are presented in Fig. 11. As can be seen, the flow behavior is well consistent with distinct regimes, which have been recognized for the IMI834 alloy in α+β region. The flow behavior of the alloy at 850 °C is similar to that at 800 °C, where at a strain rate of 0.1 s-1, the IMI834 alloy shows significant work hardening prior to UTS and beyond the UTS flow stress drops immediately. Also at strain rates of 0.001-0.01 s-1, flow stress declines much more slowly than that at 0.1 s-1. Moreover, with increasing temperature up to 950 °C or 970 °C, the flow stress beyond the UTS decreases very slowly, which is consistent with the decline in the slope of flow stress at 900 °C compared with that at 800 °C. The prediction of flow stress behavior under the conditions of which the data were not incorporated in the model was also accomplished in the work that has been done on the hot compression of Ti-6Al-7Nb alloy [20]. It has been reported that the obtained results are well consistent with the flow behavior recognized for this alloy. It can be deduced that the proposed constitutive equation for hot tension of IMI834 alloy gives an accurate estimate of the flow stress even under the conditions of which the data are not incorporated in the model.

Fig. 11 Prediction of true stress-true strain curves of IMI834 alloy in strain range of 0.08-0.22 at different temperatures and strain rates
4 Conclusions
1) At low temperatures and high strain rates, significant work hardening of IMI834 titanium alloy prior to the UTS is observed and the hot tension leads to grain boundary cracks. With decreasing the strain rate, the strain to failure increases significantly, microvoids form and coalescence of them is the main mechanism of fracture.
2) At high temperatures and low strain rates, flow behavior is steady state and dynamic recovery is the dominant mechanism. With increasing the strain rate, flow stress curves exhibit a peak stress followed by a regime down to the steady state that is related to dynamic recrystallization.
3) The activation energy in the strain range of 0.08-0.22 is obtained to be in the range of 519-557 kJ/mol at different strain in α+β region. This high value of activation energy for hot tension of IMI834 alloy is related to the flow stress values of the hard α phase and soft β phase.
4) The predictability of the proposed constitutive equation was assessed using standard statistical parameters such as correlation coefficient and average absolute relative error. The results confirmed the excellent predictability of the developed constitutive model. Also, the proposed model possesses a marked ability to estimate the flow behavior under conditions of which the data would not be incorporated in the model.
References
[1] BOYER R, WELSCH G, COLLINGS E W. Materials properties handbook: Titanium alloys [M]. ASM International, 1994.
[2] SINGH N, PRASAD N, SINGH V. On the occurrence of dynamic strain aging in near-alpha alloy Ti-5.8Al-4Sn-3.5Zr-0.7Nb- 0.5Mo-0.35Si [J]. Met Mater Trans A, 1999, 30: 2547-2549.
[3] OMPRAKASH C M, SATYANARAYANA D V V, KUMAR V. Effect of primary α content on creep and creep crack growth behaviour of near α-Ti alloy [J]. Mater Sci Technol, 2011, 27: 1427-1435.
[4] LIA L X, RAOA K P, LOUCY, PENG D S. A study on hot extrusion of Ti–6Al–4V using simulations and experiments [J]. Inter J Mech Sci, 2002, 44: 2415-2425.
[5] POLMEAR J. Light alloys from traditional alloys to nanocrystals. [M]. 4th ed. Amsterdam: Elsevier, 2006.
[6] WEISS I, SEMIATIN S L. Thermomechanical processing of alpha titanium alloys—An overview [J]. Mater Sci Eng A, 1999, 263: 243-256.
[7] WANJARA P, JAHAZI M, MONAJATI H, YUE S. Influence of thermomechanical processing on microstructural evolution in near-α alloy IMI834 [J]. Mater Sci Eng A, 2006, 416: 300-311.
[8] BEYERLEIN I, TOME C. A dislocation-based constitutive law for pure Zr including temperature effects [J]. Int J Plast, 2008, 24: 867-895.
[9] FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling [J]. Int J Plast, 2009, 25: 715-732.
[10] KHAN A S, SUH Y S, CHEN X, TAKACS L, ZHANG H. Nanocrystalline aluminum and iron: Mechanical behavior at quasi-static and high strain rates, and constitutive modeling [J]. Int J Plast, 2006, 22: 195-209.
[11] SAMANTARAY D, MANDAL S, BHADURI A K. A comparative study on Johnson Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behavior in modified 9Cr-1Mo steel [J]. Comput Mater Sci, 2009, 47: 568-576.
[12] LI J, LI F, CAI J, WANG R, YUAN Z, XUE F. Flow behavior modeling of the 7050 aluminum alloy at elevated temperatures considering the compensation of strain [J]. Mater Des, 2012, 42: 369-377.
[13] JONAS J, SELLARS C, TARGET W. Strength and structure under hot-working conditions [J]. Metall Rev, 1969, 14: 1-24.
[14] LIN Y C, CHEN M S, ZHONG J. Prediction of 42CrMo steel flow stress at high temperature and strain rate [J]. Mech Res Commun, 2008, 35: 142-150.
[15] LIN Y C, XIA Y C, CHEN X M, CHEN M S. Constitutive descriptions for hot compressed 2124-T851 aluminum alloy over a wide range of temperature and strain rate [J]. Comput Mater Sci, 2010, 50: 227-233.
[16] SAMANTARAY D, MANDAL S, BHADURI A K. Constitutive analysis to predict high-temperature flow stress in modified 9Cr-1Mo (P91) steel [J]. Mater Des, 2010, 31: 981-994.
[17] CAI J, LI F, LIU T, CHEN B, HE M. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain [J]. Mater Des, 2011, 32: 1144-1151.
[18] SESHACHARYULU T, MEDEIROS S C, FRAZIER W G, PRASAD Y V R K. Hot working of commercial Ti-6Al-4V with an equiaxed α–β microstructure: materials modeling considerations [J]. Mater Sci Eng A, 2000, 284: 184-194.
[19] SHAFAAT M A, OMIDVAR H, FALLAH B. Prediction of hot compression flow curves of Ti–6Al–4V alloy in α+β phase region [J]. Mater Des, 2011, 32: 4589-4595.
[20] PILEHVA F, ZAREI-HANZAKI A, GHAMBARI M, ABEDI H R. Flow behavior modeling of a Ti-6Al-7Nb biomedical alloy during manufacturing at elevated temperatures [J]. Mater Des, 2013, 51: 457-465.
[21] MA X, ZENGA W, SUNA Y, WANGA K, LAI Y, ZHOUA Y. Modeling constitutive relationship of Ti17 titanium alloy with lamellar starting microstructure [J]. Mater Sci Eng A, 2012, 538: 182-189.
[22] PENG W, ZENG W, WANG Q, YU H. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models [J]. Mater Des, 2013, 51: 95-104.
[23] PENG W, ZENG W, WANG Q, YU H. Characterization of high-temperature deformation behavior of as-cast Ti60 titanium alloy using processing map [J]. Mater Sci Eng A, 2013, 571: 116-122.
[24] WANJARA P, JAHAZI M, MONAJATI H, YUE S, IMMARIGEONA J P. Hot working behavior of near-α alloy IMI834 [J]. Mater Sci Eng A, 2005, 396: 50-60.
[25] VO P, JAHAZI M, YUE S, BOCHER P. Flow stress prediction during hot working of near-α titanium alloys [J]. Mater Sci Eng A, 2007, 447: 99-110.
[26] BALASUNDAR I, RAGHU T, KASHYAP B P. Modeling the high temperature deformation behaviour of a near alpha titanium alloy with bi-modal microstructure [J]. Mater Sci Forum, 2012, 710: 533-538.
[27] VANDERHASTEN M, RABET L, VERLINDEN B. Ti–6Al–4V: Deformation map and modelisation of tensile behaviour [J]. Mater Des, 2008, 29: 1090-1098.
[28] XIAO J, LI D S, LI XQ, DENG T S. Constitutive modeling and microstructure change of Ti–6Al–4V during the hot tensile deformation [J]. J Alloys Compd, 2012, 541: 346-352.
[29] KOTKUNDE N, KRISHNAMURTHY H N, PURANIK P, GUPTA A K, SINGH S K. Microstructure study and constitutive modeling of Ti–6Al–4V alloy at elevated temperatures [J]. Mater Des, 2014, 54: 96-103.
[30] MITCHELL A. Melting, casting and forging problems in titanium alloys [J]. Mater Sci Eng A, 1998, 243: 257-262.
[31] SEMIATIN S L, SEETHARAMAN V, WEISS I. Hot workability of titanium and titanium aluminide alloys—An overview [J]. Mater Sci Eng A, 1998, 243: 1-24.
[32] SEMIATIN S L, LAHOTI G D. Deformation and unstable flow in hot forging of Ti-6Ai-2Sn-4Zr-2Mo-0.1Si [J]. Metal Trans A, 1981, 12: 1705-1717.
[33] DADRAS P, THOMAS J F. Characterization and modeling for forging deformation of Ti-6Ai-2Sn-4Zr-2Mo-0.1 Si [J]. Metal Trans A, 1981, 12: 1867-1876.
[34] VO P, JAHAZI M, YUE S. Recrystallization during thermomechanical processing of IMI834 [J]. Met Mater Trans A, 2008, 39: 2965-2980.
[35] VANDERHASTEN M, RABET L, VERLINDEN B. Deformation mechanisms of Ti-6Al-4V during tensile behavior at low strain rate [J]. J Mater Eng Performance, 2007, 16: 208-212.
[36] JIA W, ZENGA W, LIU B J, ZHOUA Y, WANG Q. On the influence of processing parameters on microstructural evolution of a near alpha titanium alloy [J]. Mater Sci Eng A, 2011, 530: 135-143.
[37] MINTZ B, SHAKER M, CROWTHER D N. Hot ductility of an austenitic and a ferritic stainless steel [J]. Mater Sci Technol, 1997, 13: 243-250.
[38] SEMIATIN S L, SEETHARAMAN V, GHOSH A K, SHELL E B, SIMON M P, FAGIN P N. Cavitation during hot tension testing of Ti-6Al-4V [J]. Mater Sci Eng A, 1998, 256: 92-110.
[39] SELLARS C M, TEGART W J. On the mechanism of hot deformation [J]. Acta Metall, 1966, 14: 1136-1138.
[40] LIU Y, NING Y, YAO Z, GUO H. Hot deformation behavior of Ti–6.0Al–7.0Nb biomedical alloy by using processing map [J]. J Alloys Compd, 2014, 587: 183-189.
[41] JIA W, ZENG W, ZHOU Y, LIU J, WANG Q. High-temperature deformation behavior of Ti60 titanium alloy [J]. Mater Sci Eng A, 2011, 528: 4068-4074.
[42] HANA Y, ZENG W, QI Y, ZHAO Y. Optimization of forging process parameters of Ti600 alloy by using processing map [J]. Mater Sci Eng A, 2011, 529: 393-400.
[43] LI L X, LOU Y, YANG L B, PENG D S, RAO K P. Flow stress behavior and deformation characteristics of Ti-3Al-5V-5Mo compressed at elevated temperatures [J]. Mater Des, 2002, 23: 451-457.
[44] LIU B, LI Y P, MATSUMOTO H, LIU Y B, LIU Y, CHIBA A. Thermomechanical characterization of P/M Ti-Fe-Mo-Y alloy with a fine lamellar microstructure [J]. Mater Sci Eng A, 2011, 528: 2345-2352.
[45] MOMENI A, ABBASI S M. Effect of hot working on flow behavior of Ti-6Al-4V alloy in single phase and two phase regions [J]. Mater Des, 2010, 31: 3599-3604.
[46] MANDAL S, SIVAPRASAD P V, VENUGOPAL S, MURTHY K P N. Artificial neural network modeling to evaluate and predict the deformation behavior of stainless steel type AISI 304L during hot torsion [J]. Appl Soft Comput, 2009, 9: 237-244.
[47] PHANIRAJ M P, LAHIRI A K. The applicability of neural network model to predict flow stress for carbon steels [J]. J Mater Process Technol, 2003, 141: 219-227.
M. H. GHAVAM, M. MORAKABATI, S. M. ABBASI, H. BADRI
Metallic Materials Research Center, Maleke Ashtar University of Technology, Tehran 009821, Iran
摘 要:建立合适的本构模型预测IMI834钛合金在α+β区的热拉伸流变行为。热拉伸实验在温度为800~1025 °C、应变速率为0.001~0.1 s-1条件下进行。此本构模型通过Arrhenius型方程来表征应变为0.08~0.22时合金的热拉伸行为。结果表明,在不同应变条件下IMI834钛合金的热拉伸变形激活能范围为519~557 kJ/mol。利用标准统计参数估算预测合金流变应力曲线的精度。所预测的合金的流变应力曲线与实验结果十分吻合。
关键词:钛合金;流变行为;热拉伸变形;本构方程
(Edited by Wei-ping CHEN)
Corresponding author: M. MORAKABATI; Tel: +98-21-77591539; Fax: +98-21-44562065; E-mail: m_morakabati@iust.ac.ir
DOI: 10.1016/S1003-6326(15)63660-3

