J. Cent. South Univ. (2019) 26: 839-851

DOI: https://doi.org/10.1007/s11771-019-4053-3

Optimal design and applicability of electric power steering system for automotive platform

Abolfazl KHALKHALI, Mohammad Hassan SHOJAEEFARD,Masoud DAHMARDEH, Hadi SOTOUDEH

Automotive Simulation and Optimal Design Research Laboratory, School of Automotive Engineering,Iran University of Science and Technology, Tehran, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The ongoing need for better fuel economy and lower exhaust pollution of vehicles has increased the employment of electric power steering (EPS) in automotives. Optimal design of EPS for a product family reduces the development and fabrication costs significantly. In this paper, the TOPSIS method along with the NSGA-II is employed to find an optimum family of EPS for an automotive platform. A multi-objective optimization problem is defined considering road feel, steering portability, RMS of Ackerman error, and product family penalty function (PFPF) as the conflicting objective functions. The results for the single objective optimization problems and the ones for the multi-objective optimization problem, as well as two suggested trade-off design points are presented, compared and discussed. For the two suggested points, performance at one objective function is deteriorated by about 1%, while the commonality is increased by 20%–40%, which shows the effectiveness of the proposed method in first finding the non-dominated design points and then selecting the trade-off among the obtained points. The results indicate that the obtained trade-off points have superior performance within the product family with maximum number of common parts.

Key words: product family optimization; optimal platform design; NSGA-II; TOPSIS; electric power steering

Cite this article as: Abolfazl KHALKHALI, Mohammad Hassan SHOJAEEFARD, Masoud DAHMARDEH, Hadi SOTOUDEH. Optimal design and applicability of electric power steering system for automotive platform [J]. Journal of Central South University, 2019, 26(4): 839–851. DOI: https://doi.org/10.1007/s11771-019-4053-3.

1 Introduction

In recent years, the demand for high variety products in the automotive section has been increased significantly. To meet various customer needs and the broad satisfaction requirements, it is necessary for the manufacturing companies to produce high variety of products with the lowest possible costs. In order to solve the trade-off between product, variety and cost several approaches are proposed; one of the most effective methods is adopting the product family design and platform-based production [1, 2]. Product family design approach, by increasing the use of common parts, produces a family of product variants derived from a common platform [3], and each product satisfices a segment of market [4]. Due to the parametric nature of the product family design, developing a suitable optimization method plays an important role in finding the optimal solutions or Pareto frontier [5]. To achieve this, several efforts have been made such as the work by CHANG et al [6] in which they reported a robust design technique to develop a family of automotive A/C units. Identification of the platform based on the performance deviation vector was carried out by FELLENI et al [7]. SIMPSON et al [8] employed product platform concept exploration method (PPCEM) to optimize a family of electric motors. In order to quantify the commonality of the common parts among products, MESSAC et al [9] introduced the product family penalty function (PFPF) as a new optimization target. This enables a proper balance between commonality and performance within the product family. AKUNDI et al [10] carried out genetic algorithm (GA) optimization to optimize a universal motor product family. Some other works [11, 12] investigated the platform-based design optimization methods. There are two approaches for solving platform-based design optimization problems. In the first approach, two-stage approach, common parameters are defined in the first stage, then the individual parameters are optimized in the second stage [11]. In the second approach, single-stage approach, common parameters and individual ones are defined and optimized simultaneously. Although, both approaches are popular, however, the single- stage one, in which all the optimization objectives are considered simultaneously, is believed to provide more accurate results [13]. The non- dominated sorting genetic algorithm (NSGA-II) as a popular non-dominated multi-objective optimization technique is introduced by SRINIVAS et al [14]. Advantages of this method compared to other multi-objective optimization techniques are discussed in Ref. [15]. NSGA-II is a popular non- domination multi-objective optimization method employed by many researchers [16–19].

During product family platform design, it is desired to maximize the number of common parts among the family, while increasing individual product performance. However, increasing the performance leads to a unique design for each product, which is not desirable due to economic reasons. Therefore, this introduces a commonality/ performance trade-off problem during the product family platform design. Non-dominated sorting algorithms essentially provide non-dominated points as final solution and the designer should choose a point among them. Therefore, it is desired to find a trade-off between optimum design points within all non-dominated individuals. On the other hand, multiple-criteria decision making (MCDM) methods are employed to determine the optimal trade-off points among the non-dominated solution points. The technique for ordering preferences by similarity to ideal solution (TOPSIS) is a powerful MCDM method to determine the trade-off points among all non-dominated optimal solutions [20]. TOPSIS finds optimum points based on the principle that the trade-off points have the smallest distance to the positive optimal point and farthest distance to the negative optimal point, simultaneously. A novel approach in solving product family platform design problems is to employ TOPSIS method along with the NSGA-II. This approach increases the probability of success for optimal design and is reported for the first time in Ref. [21] and demonstrated the effectiveness of this method.

There is an increasing demand for better fuel economy and lower exhaust pollution of vehicles. New combustion technology [22–24] and after- treatment methods [25, 26] are investigated thoroughly to answer this challenge. On the other hand, electric power steering (EPS) system utilizes an electric motor to provide steering assist. Compared to the conventional hydraulic steering system, EPS excels in many aspects such as safety, cost, fuel consumption, and assembly and is believed to be the future power-assisted steering system for passenger cars. The increasing use of electric power steering system highlights the need for an accurate model, which motivated the researchers to propose several models for the system. Integrated simulation of EPS control system with full-vehicle dynamic model is reported and its effect on the handling performance is studied [27]. Robust control strategy is employed to increase stability and efficiency of EPS [28]. The effect of EPS system on the road feel and vehicle handling stability is investigated and a dynamic compensation controller is developed to improve the stability [29]. Dynamic model of the EPS system is presented and system parameters are optimized considering road feel and steering portability as the optimization targets [30, 31]. Due to the importance of EPS system in making the vehicle more energy efficient, compact and lightweight, it is vital to design EPS systems with maximum performance as well as maximum commonality of parts for a family of automotive products.

In this article, the novel approach of employing TOPSIS algorithm along with the NSGA-II method for the optimal design of a product family of electric power steering system is presented. The proposed approach increases the chance of success in the optimal design of a product family. The platform consists of five different types of automotives, sedan, hatchback, SUV, minivan, and pickup. First, a three-degrees-of-freedom bicycle model is presented. The EPS mathematical model is presented and four objective functions are considered; road feel, steering portability, RMS of Ackerman error, and PFPF. The product performance is described by the first three objective functions, while the fourth one is a representation of the commonality of the sub-systems. Six design constrains are considered; the reduction gear on the rack and electromotor, the rigidity coefficient of twisting rod, the steering arm’s length, the tie rod’s length, and the distance from the front wheel axis to the rack axis. Optimal design of the EPS system for the product family is carried out using NSGA-II, considering not only the best performance of the EPS system for each product, but also the commonality of the design parts. After finding the non-dominated optimal solutions, TOPSIS is employed to choose the trade-off points among them. The results indicate the effectiveness of the proposed method in optimal design of product family.

2 Methodology

2.1 Electric power steering model

2.1.1 Vehicle model

In order to control the vehicle to follow the desired path, a simple yet reliable vehicle model is required. Although, complex vehicle models are available, however, the three degrees of freedom (3-DoF) bicycle model considering yaw motion, lateral motion and roll angle as shown in Figure 1 is employed to investigate the effects of EPS on the overall performance of the vehicle [32].

The vehicle dynamic equations can be described as follows:

    (1)

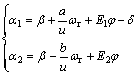                    (2)

where D₁ and D₂ are the roll damping coefficients of front and rear suspensions; C_φ1 and C_φ2 are the roll stiffness coefficient of front and rear suspensions; c_f and c_r are the cornering stiffness; φ is the roll angle; β is the sideslip angle; E₁ and E₂ are the front and rear roll steer coefficients, respectively.

Figure 1 Schematic view of bicycle vehicle dynamic model

An EPS system is shown in Figure 2, which consists of torque sensor, speed sensor, electric control unit (ECU), reduction gear and assist motor [29].

Figure 2 Schematic view of electric power steering system

The torque sensor measures the torque acting upon the steering wheel, while the vehicle speed sensor reads the vehicle speed, simultaneously. The sensors output signals are sent to the ECU, where the command signal is generated and is sent to the electric motor to produce the required assisting steering torque. The torque produced by the motor is transmitted to the steering column through electromagnetic clutch and reduction gear.

,

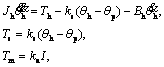
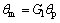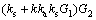                       (3)

where J_h, B_h, T_h and θ_h are the steering column moment of inertia and damping coefficient, the torque acting on the steering wheel, and the steering wheel angle, respectively; J_m, B_m, T_m and θ_m are the electromotor moment of inertia and damping coefficient, the torque acting on the electromotor and the electromotor angle; J_r and B_r are the rack moment of inertia and damping coefficient; G₁ and G₂ are the reduction gears on the rack and the electromotor, respectively.

2.1.2 Ackerman steering error

Figure 3 shows a front-wheel-steering vehicle that is turning left. In order for the inner and outer wheels to turn slip-free, a kinematic condition, known as the Ackerman condition, should be fulfilled. In other words, Ackerman geometry essentially provides the appropriate steering angles for the inner and outer wheels so that the tires experience pure rolling during a turn and do not scrub, which in turn improve the handling. Equation 4 expresses the Ackerman condition, where δ_i and δ_o are the steer angles of the inner and outer wheels, respectively; T is the distance between the steer axes of the wheels (the track); and is the distance between the front and rear axles (the wheelbase) [32].

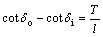                         (4)

Figure 3 Ackerman principle schematic

The widely used rack-and-pinion steering linkage mechanism have two common configurations: central take-off (CTO), where the tie rod connects at the center point of the rack and side take-off (STO), where the tie rods connect to the end points of the rack [33]. In this article, the CTO configuration is selected as the steering mechanism. Practically, it is desired that the steering system follows the Ackerman geometry exactly, however, there is always an error between the two. The actual steering path and the Ackerman geometry are shown in Figure 4 and are formulated as follows.

Figure 4 Six-bar planar rack-and-pinion steering linkage for the CTO configuration

The expression of the rack displacement, x, can be calculated using Eqs. (5) and (6).

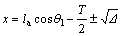                      (5)

                (6)

The calculation details are given in Appendix A.

The root-mean-square (RMS) function of the output steering error angle is given by Eq. (7). θ_6A is the Ackerman value for the θ₆ as shown in Figure 4.

                 (7)

2.1.3 Road feel

In order to characterize the way the driver feels the road and the way the condition between the road and tires are transmitted to the driver, the road feel function is introduced and is defined as the ratio of the steering wheel torque to the resistance torque acting on the tire [29, 31]. The resistance torque without considering the effects of linkage configuration and pinion effects is calculated in the previous section. Considering these effects, the expression can be formulated as below.

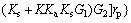                  (8)

And the road feel objective function for the frequency range of up to ω₀=40 Hz, is expressed by Eq.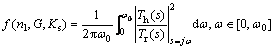(9).

  (9)

2.1.4 Steering portability

Steering portability is a representation of the maneuvering performance of the vehicle and is a measure of handling performance and vehicle maneuverability. The steering portability is defined as the ratio of yaw rate velocity to the steering wheel angle [30] and can be expressed as follows:

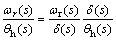                      (10)

where

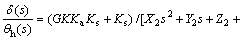
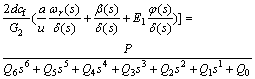 (11)

and,

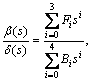
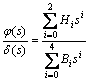                          (12)

The parameters Q₀ to Q₆ given in Eq. (11) are calculated as:

,

,

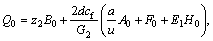
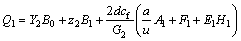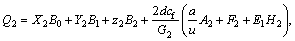
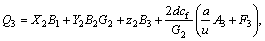
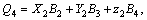
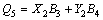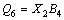                             (13)

The unknown coefficients and more details for calculating Eqs. (12) and (13) are given in the Appendix A. The objective function for the steering portability is considered according Eq. 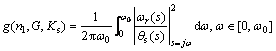(14).

 (14)

2.2 Optimal platform design problem

Platform-based design approach not only considers all the design constrains and performance requirements related to individual products, but also tries to increase the use of common parts within the family. In product family design approach, it is vital to choose an appropriate platform structure (i.e., the common parts), and to achieve maximum possible performance for each product by designing individual parameters. Therefore, a multi-objective optimization technique helps determining the optimum non-dominated points, known as the Pareto frontier, and determining the platform variables, simultaneously. Therefore, a platform- based design can be carried out by solving a multi- objective optimization problem [3]. In this article, the product family optimization process is carried out in a single-stage approach. General form of such optimization problem can be expressed as follows:

 (15)

where PFPF is the product family penalty function [21] and determines which variables have the largest impact on the performance to drive commonality. It helps to decrease the variation of variables within the family by minimizing the percent variation.

To solve the above optimization problem, non- dominated sorting genetic algorithm (NSGA-II) as a powerful optimization algorithm is used. A chromosome string with a length of n×p genes is generated, where n determines the number of design variables for each product and p defines the number of products in the product family. The NSGA-II is modified to assess commonality between design variables within the family. Therefore, a set of n×1 genes is augmented to the chromosome to specify the commonality or individuality of each design variable. These genes can have a value of either 0 or 1. The value of 0 means that the respective design variable is not common among the platform products, and the value of 1 shows that the corresponding design variable is consistent for all products. Therefore, the chromosome string has an overall length of n×(p+1). If the first n genes are all 1, there is a one hundred percent commonality of design variables among the product family, and if they are all 0, there is no common design variable among the product family.

2.3 Application to automotive electric power steering system

The proposed case study is the electric power steering of NP01, the national automotive platform. This platform is under development at the School of Automotive Engineering, Iran University of Science and Technology. The product family composed of five types of vehicles; sedan (classified as D-class), hatchback (classified as B-class), SUV, minivan (classified as MPV class) and pick-up. The vehicle schematics and specifications are presented in Figure 5 and Table 1, respectively.

The problem consists of four conflicting objective functions, in such a way that improving one function deteriorates the other ones. Therefore and initially, the proposed multi-objective optimization problem of the EPS system for the mentioned vehicle family is solved using NSGA-II method, in order to find the non-dominated optimum set of solutions, known as the Pareto optimum points. The non-dominated points are presented in the space of the objective functions in order to show the superiority of these points compared to the rest of design points. It should be noted that the non-dominated optimum points are not optimum for all four objective functions, simultaneously. Later, the technique for order performance by similarity to ideal solution (TOPSIS method) is employed to find the trade-off optimum point. The three objective functions, road feel (RF), steering portability (SP), and RMS of Ackerman error (AR), are employed to define the performance of the electric power steering system for the proposed family of five types of vehicles.

Figure 5 Schematic view of proposed product family

Table 1 Specifications of vehicles within product family

While, the PFP function, as the fourth objective function, is considered to increase the commonality of the design variables within the vehicle family.

Design variables of the case study are shown below and the corresponding bounds are listed in Table 2.

Table 2 Design variables constrains

The multi-objective optimization problem can be formulated as follows.

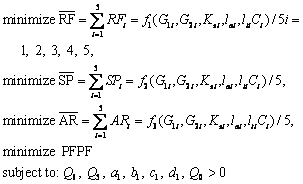 (16)

Unequal constrains stated in Eq. (16) are due to the fact that the first column of the Routh–Hurwitz equation should be positive. The Routh-Hurwitz equations are derived in the Appendix A.

3 Results and discussion

A population of 60 individuals with a crossover probability of 0.7 and a mutation probability of 0.07 is used with 500 generations for the proposed 4-objective optimization problem. Figures 6–9 illustrate the non-dominated individual points in the planes of (RF-SP), (SP-AC), (RF-AC), and (PFPF-AC), respectively. It should be noted that the results of the 4-objective optimization problem include results of the single objective optimization problems. For example, the design point ‘A’ is the result of a single objective optimization of the road-feel function. Therefore, if the designer wants to minimize the road-feel function, the design point ‘A’ is suggested. Similarly, the design points ‘B’, ‘C’ and ‘D’ are the results of single objective optimization of steering portability, RMS of Ackerman error, and PFPF functions, respectively. These optimum design points are shown in Figures 6–9 and the values of the associated design variables and objective functions are listed in Tables 3–8. It should be noted that there are some points in each plane that may dominate others considering only a 2-objective optimization problem.

Figure 6 Pareto front of road feel (RF)–steering portability (SP) within product family

Figure 7 Pareto front of RMS of Ackerman error– steering portability within product family

Figure 8 Pareto front of RMS of Ackerman error–road feel within product family

Figure 9 Pareto front of RMS of Ackerman error–product family penalty function

As it can be seen from Figure 6, among the non-dominated points,point ‘B’ which corresponds to the result of the single-objective optimization of steering portability function, has very low values for both steering portability and road feel functions in the plane of (RF-SP). However, in Figure 7, one can quickly see that this point has the highest value for the RMS of the Ackerman error.

This indicates that point ‘B’ is not the desired point in the viewpoint of all objective functions, simultaneously. Similarly, point ‘C’ which corresponds to the single-objective optimization of RMS of Ackerman error, has the lowest value of Ackerman error (Figure 7), while its corresponding values for the road feel and steering portability functions are in the middle range of the possible solutions (Figure 6). Also, point ‘A’ which corresponds to the single-objective optimization of the road feel function, has the lowest value for the road feel function, but has high values for both steering portability and Ackerman error functions. On the other hand, it is obvious that as the PFPF function decreases, the commonality of the design variables within the product family increases, which may degrade product performance. This is essentially clear from observing point ‘D’, which is the solution of a single-objective optimization of the PFPF function in Figures 6–9. Interesting results shown in Figure 9 is that all optimum points obtained from single-objective optimization have low values for the PFPF function, compared to all other obtained non-dominated results. This enables the designer to select a priority for the objective functions while obtaining a high level of commonality. These individuals are all non- dominated considering all four objective functions, simultaneously.

Therefore, it is desired to find a trade-off between optimum design points within all non-dominated individuals. The proposed algorithm employs TOPSIS method, which finds the optimum points having the smallest distance to the positive ideal solution and largest distance from the negative ideal solution, simultaneously. Hence, the optimum point ‘E’ is calculated based on the TOPSIS method considering equal weights for all objective functions. This point has low values for the Ackerman function, moderate values for steering portability and road feel functions, and good values for the PFPF, which shows the high commonality of the design variables for this point.

The obtained non-dominated points in the planes of (SP-AC) and (RF-AC) are along Pareto fronts. On the other hand, considering (RF-SP) plane, a point can be selected in such a way that it minimizes the two objective functions, simultaneously (point ‘F’). The Ackerman error function for this point is in the moderate range, and comparing with the optimal point with the best Ackerman error function (point ‘C’), the error is almost twice. On the other hand, the PFPF function associated with the point ‘F’ is very good. It should be noted that all the provided optimum points might be chosen by the designer, according to their design priority.

Considering the obtained design variables associated with design points A–F (Tables 3–8), it can be seen that the design variable G₁ is always considered as a common parameter. Therefore, the reduction gear on the rack can be considered common by the designer of the platform. On the other hand, the design variable L_t is always unique for each product variants. Therefore, the designer needs to have separate design values for the tie rod’s length for each product. Such interesting design concepts could not be obtained without using the method employed in this article.

Table 3 Value of design variables for product family ‘A’

Table 4 Value of design variables for product family ‘B’

Table 5 Value of design variables for product family ‘C’

Table 6 Value of design variables for product family ‘D’

Table 7 Value of design variables for product family ‘E’

Table 8 Value of design variables for product family ‘F’

In order to further illustrate the effect of selecting each non-dominated design point on the objective functions, Bode diagrams of the road feel objective function for the suggested optimum design points are plotted (Figures 10 and 11). As it is expected, the suggested optimum point with the minimum value for the road feel objective function (point ‘A’), has the best performance, compared with the other design points.

Figure 10 Bode diagram (magnitude) of road feel function for five non-dominated optimum design points

Figure 11 Bode diagram (phase) of road feel function for five non-dominated optimum design points

Table 9 shows a comparison for the obtained values of the objective functions at different optimum points. As can be seen, point “C” has the lowest value for the Ackerman error function, and this value is very close to the one obtained for point “E” which is the result of TOPSIS (0.9% deterioration). However, the number of common design variables for point “C” is 2 (Table 5), while the number of common design variables for point “E” is 3 (Table 7). Therefore, the commonality is improved for point “E”, compared with point “C” (50% compared with 33%). On the other hand, point “F” has good values for the road feel function, compared with the best obtained value of the road feel function which belongs to point “A”. Essentially, this value for point “F” is 1% worse than the one for point “A”. However, the level of commonality is improved from 16% at point “A” to 50% at point “F”. To conclude, it can be seen that the first suggested point obtained from the TOPSIS method (point ‘E’) with equal weighting factor has an acceptable value in terms of the road feel function, but with the advantage of more commonality. On the other hand, the second suggested point “F” shows good behavior in terms of performance objective functions, with the advantage of higher commonality. It should be noted that there is a trade-off between increasing the commonality of the design variables and increasing the performance of the overall objective functions of the system. Therefore, several optimum design points are suggested, and the auto maker might choose any of them, depending on which side of the trade-off is prioritized, increasing the commonality or the performance.

Table 9 Objective function values at optimum points

It is obvious that the obtained design points are the best possible values among all design points. Besides non-dominated optimal points, other design points show lower performance in terms of the objective functions, as well as lower commonality among design variables, which leads to high manufacturing and production costs.

4 Conclusions

A platform-based optimization approach is demonstrated to determine design variables of an electric power steering (EPS) system within a product family of five different types of vehicle. The NSGA-II method is utilized for the optimization of the 3-DoF vehicle model. The multi-objective optimization problem consists of four conflicting objective functions. The three objective functions, road feel (RF), steering portability (SP), and RMS of Ackerman error (AR) are considered to improve performance of the EPS system for the proposed family. Concurrently, the PFPF function, as the fourth objective function, is considered to increase the commonality of the design variables within the vehicle family. The TOPSIS method using equal weighting factor for all objective functions is applied to finding the trade-off design points among the obtained Pareto front. Also, five design points obtained by single- objective optimization process for each objective function are presented. The results show that by increasing the PFPF weighting factor, the commonality is increased, which in turn, decreases the performance due to the inherent conflict between commonality and performance. However, the proposed method provides design points with the benefit of having good performance, while increasing the commonality. The first suggested trade-off point obtained using TOPSIS considering equal weights for all objective functions (point ‘E’) has slightly higher Ackerman error compared with the single objective optimization for Ackerman, however, 50% of the design variables are common for this point, compared to the 33% value for the single objective optimization result. The second suggested point, which minimizes the two objective functions of the (RF-SP) plane, simultaneously (point ‘F’) has slightly higher road feel value compared with the point obtained using single objective optimization for the road feel function, however, 50% of the design variables are common for this point, compared to the 16% value for the single objective optimization result. However, at the end, the designer needs to prioritize the desired objective function and select the desired optimum point which corresponds to the optimum design variables. Future work might be employing two-stage optimization procedure to solve the proposed problem. Another direction of the future work might be to consider different design variables and/or considering controlling approach of the proposed EPS system and compare the results with the presented ones.

Appendix

,

,

,

,

,

,

,

,

,

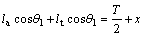
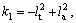
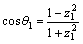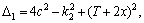
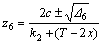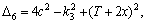
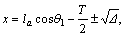
The index of the steering portability equation

,

,

,

,

,

,

,

,

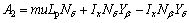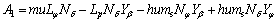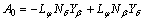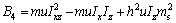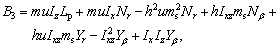
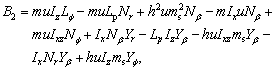
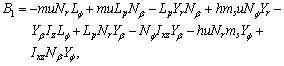
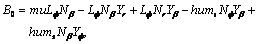
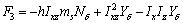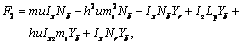
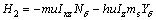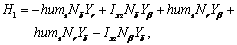
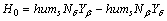In which

,

,

,

,

,

,

,

,

,

,

,

,

,

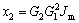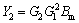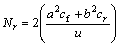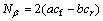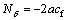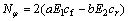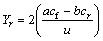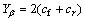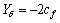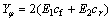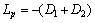The Routh list of equation expressed as

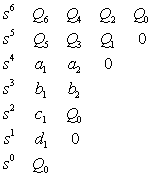
where

.

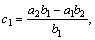
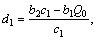
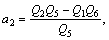
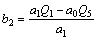References

[1] PARK J, SIMPSON T W. Toward an activity-based costing system for product families and product platforms in the early stages of development [J]. International Journal of Production Research, 2008, 46(1): 99–130. DOI: 10.1080/00207540600825240.

[2] MARION T J J, THEVENOT H J J, SIMPSON T W W. A cost-based methodology for evaluating product platform commonality sourcing decisions with two examples [J]. International Journal of Production Research, 2007, 45(22): 5285–5308. DOI: 10.1080/00207540600710970.

[3] SIMPSON T W, SIDDIQUE Z, JIAO J R. Platform-based product family development [C]// Product Platform and Product Family Design. Boston, MA, US: Springer. DOI: 10.1007/0-387-29197-0_1.

[4] MEYER M H, LEHNERD A P. The power of product platforms: Building value and cost leadership [M]. New York,: Simon and Schuster, 1997: 39.

[5] SIMPSON T T W T, SIDDIQUE Z, JIAO R J R. Product platform and product family design, methods and applications [M]. New York: Springer, 2006.

[6] CHANG T S, WARD A C. Design-in-modularity with conceptual robustness. Advances in Design Automation [J]. ASME, 1995, 82(1): 493–500.

[7] FELLINI R, KOKKOLARAS M, MICHELENA N, PAPALAMBROS P, PEREZ-DUARTE A, SAITOU K, FENYES P. A sensitivity-based commonality strategy for family products of mild variation, with application to automotive body structures [J]. Structural and Multidisciplinary Optimization, 2004, 27(1, 2): 89–96. DOI: 10.1007/s00158-003-0356-x.

[8] SIMPSON T W, MAIER J R A, MISTREE F. A product platform concept exploration method for product family design [C]// ASME Design Theory and Methodology. Las Vegas: ASME, 1999: DTM8761.

[9] MESSAC A, MARTINEZ M P M P, SIMPSON T W T W. Introduction of a product family penalty function using physical programming [J]. Journal of Mechanical Design, 2002, 124(2): 164–172. DOI: 10.1115/1.1467602.

[10] AKUNDI S, SIMPSON T W, REED P M. Multi-objective design optimization for product platform and product family design using genetic algorithms [C]// 31st Design Automation Conference, Parts A and B, vol. 2005. Long Beach, CA,: ASME, 2005: 999–1008. DOI: 10.1115/ DETC2005-84905.

[11] SIMPSON T W, D’SOUZA B S. Assessing variable levels of platform commonality within a product family using a multiobjective genetic algorithm [J]. Concurrent Engineering, 2004, 12(2): 119–129. DOI: 10.1177/1063293X04044383.

[12] CETIN O L, SAITOU K. Decomposition-based assembly synthesis for structural modularity [J]. Journal of Mechanical Design, 2004, 126(2): 234. DOI: 10.1115/1.1666890.

[13] MESSAC A, MARTINEZ M P, SIMPSON T W. Effective product family design using physical programming [J]. Engineering Optimization, 2002, 34(3): 245–261. DOI: 101080/030521502117462010.

[14] SRINIVAS N, DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms [J]. Evolutionary Computation, 1994, 2(3): 221–248. DOI: 10.1162/evco. 1994.2.3.221.

[15] DEB K, PRATAP A, AGARWAL S, MEYARIVAN T. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. DOI: 10.1109/4235.996017.

[16] MOZAFFARI A, VAJEDI M, CHEHRESAZ M, AZAD N L. Multi-objective component sizing of a power-split plug-in hybrid electric vehicle powertrain using Pareto-based natural optimization machines [J]. Engineering Optimization, 2016, 48(3): 361–379. DOI: 10.1080/0305215X.2015.1012075.

[17] KIM Y G, LEE J. Fatigue design of a cellular phone folder using regression model-based multi-objective optimization [J]. Engineering Optimization, 2016, 48(8): 1275–1295. DOI: 10.1080/0305215X.2015.1099641.

[18] ZHAO An, LAI Zhou-nian, WU Peng, CAO Lin-lin, WU Da-zhuan. Multi-objective optimization of a low specific speed centrifugal pump using an evolutionary algorithm [J]. Engineering Optimization, 2016, 48(7): 1251–1274. DOI: 10.1080/0305215X.2015.1104987.

[19] KHALKHALI A. Best compromising crashworthiness design of automotive S-rail using TOPSIS and modified NSGAII [J]. Journal of Central South University, 2015, 22(1): 121–133. DOI: 10.1007/s11771-015-2502-1.

[20] HWANG C L, YOON K. Methods for multiple attribute decision making [M]. Berlin, Heidelberg: Springer, 1981. DOI: 10.1007/978-3-642-48318-9_3.

[21] SHOJAEEFARD M H, KHALKHALI A, FAGHIHIAN H, DAHMARDEH M. Optimal platform design using non-dominated sorting genetic algorithm II and technique for order of preference by similarity to ideal solution; application to automotive suspension system [J]. Engineering Optimization, 2018, 50(3): 471–482. DOI: 10.1080/ 0305215X.2017.1324853.

[22] DENG Y W, LIU H W, ZHAO X H, E J Q, CHEN J M. Effects of cold start control strategy on cold start performance of the diesel engine based on a comprehensive preheat diesel engine model [J]. Applied Energy, 2018, 210: 279–287. DOI: 10.1016/j.apenergy.2017.10.093.

[23] E J Q, ZHANG Z Q, TU Z F, ZUO W, HU W Y, HAN D D, JIN Y. Effect analysis on flow and boiling heat transfer performance of cooling water-jacket of bearing in the gasoline engine turbocharger [J]. Applied Thermal Engineering, 2018, 130: 754–766. DOI: 10.1016/ j.applthermaleng.2017.11.070.

[24] E J Q, HAN D D, DENG Y W, ZUO W, QIAN C, WU G, PENG Q G, ZHANG Z Q. Performance enhancement of a baffle-cut heat exchanger of exhaust gas recirculation [J]. Applied Thermal Engineering, 2018, 134: 86–94. DOI: 10.1016/ j.applthermaleng.2018.01.109.

[25] E J Q, ZUO Q S, LIU H L, LI Y, GONG J K. Endpoint forecasting on composite regeneration by coupling cerium-based additive and microwave for diesel particulate filter [J]. Journal of Central South University, 2016, 23(8): 2118–2128. DOI: 10.1007/s11771-016-3268-9.

[26] ZUO Q S, E J Q, GONG J K, ZHANG D M, CHEN T, JIA G hai. Performance evaluation on field synergy and composite regeneration by coupling cerium-based additive and microwave for a diesel particulate filter [J]. Journal of Central South University, 2014, 21(12): 4599–4606. DOI: 10.1007/s11771-014-2466-6.

[27] LIAO Y G, DU H I. Cosimulation of multi-body-based vehicle dynamics and an electric power steering control system [J]. Journal of Multi-Body Dynamics, 2001, 215(3): 141–151. DOI: 10.1243/1464419011544420.

[28] ZHAO W Z, SHI G B, LIN Y, NIE H. Tracking performance of electric power steering system based on the mixed h₂/h_∞ strategy [J]. Chinese Journal of Mechanical Engineering 2011, 24(4): 584–590.

[29] ZANG H Q, GENG J. Effects and solution of electric power steering system on vehicle handling stability [J]. Journal of Computational Information Systems, 2012, 8(1): 65–72.

[30] ZHAO W Z, ZHAO T, LI Y J, WANG C Y, ZHANG Z Q, DUAN T T. Integration optimization of novel electric power steering system based on quality engineering theory [J]. Journal of Central South University, 2013, 20(6): 1519–1526. DOI: 10.1007/s11771-013-1643-3.

[31] ZHAO W, WANG C, SUN P, LIU S. Primary studies on integration optimization of differential steering of electric vehicle with motorized wheels based on quality engineering [J]. Science China Technological Sciences, 2011, 54(11): 3047–3053. DOI: 10.1007/s11431-011-4565-z.

[32] JAZAR R N. Vehicle dynamics: Theory and application [M]. Boston, MA: Springer, 2008. DOI: 10.1007/978-0- 387-74244-1.

[33] RAHMANI HANZAKI A, RAO P V M, SAHA S K. Kinematic and sensitivity analysis and optimization of planar rack-and-pinion steering linkages [J]. Mechanism and Machine Theory, 2009, 44(1): 42–56. DOI: 10.1016/ j.mechmachtheory.2008.02.014.

(Edited by HE Yun-bin)

中文导读

汽车平台电动转向系统的优化设计及适用性

摘要：对更好的燃油经济性和降低汽车尾气污染的持续需求增加了电动转向(EPS)在汽车中的应用。产品系列的EPS优化设计可大大降低开发和制造成本。本文采用TOPSIS和NSGA-II相结合的方法，寻找汽车平台EPS的最优系列，提出了一个多目标优化问题.该问题将道路感、转向便携性、Ackerman误差的均方根和产品系列罚函数作为相互制约的目标函数。给出了单目标优化问题和多目标优化问题的结果，并提出了两个折衷设计点，进行了比较和讨论。对于这两个折衷设计点，一个目标函数的性能下降了约1%，而共性增加了20%~40%，说明了该方法在首先找到非主导设计点，然后在得到的点之间进行权衡的有效性。结果表明，所得到的折衷点在公共部件数量最大的产品系列中具有较好的性能。

关键词：产品系列优化；最优平台设计；NSGA-II；TOPSIS；电动助力转向

Received date: 2017-11-03; Accepted date: 2018-05-24

Corresponding author: Abolfazl KHALKHALI, PhD, Associate Professor; Tel: +98-2173223961; E-mail: ab_khalkhali@iust.ac.ir; ORCID: 0000-0003-1179-1963