Trans. Nonferrous Met. Soc. China 28(2018) 340-347
Constitutive modeling for dynamic recrystallization kinetics of Mg-4Zn-2Al-2Sn alloy
Dong-qing ZHAO1,2, Yuan-sheng YANG1,2, Ji-xue ZHOU1,3, Yu LIU1, Shou-qiu TANG1,3
1. Shandong Provincial Key Laboratory for High Strength Lightweight Metallic Materials,
Advanced Materials Institute, Qilu University of Technology (Shandong Academy of Sciences), Ji’nan 250014, China;
2. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China;
3. Shandong Engineering Research Center for Lightweight Automobiles Magnesium Alloy, Advanced Materials Institute, Qilu University of Technology (Shandong Academy of Sciences), Ji’nan 250014, China
Received 26 September 2016; accepted 12 April 2017
Abstract: In order to have a better understanding of the hot deformation behavior of the as-solution-treated Mg-4Zn-2Sn-2Al (ZAT422) alloy, a series of compression experiments with a height reduction of 60% were performed in the temperature range of 498-648 K and the strain rate range of 0.01-5 s-1 on a Gleeble 3800 thermo-mechanical simulator. Based on the regression analysis by Arrhenius type equation and Avrami type equation of flow behavior, the activation energy of deformation of ZAT422 alloy was determined as 155.652 kJ/mol, and the constitutive equations for flow behavior and the dynamic recrystallization (DRX) kinetic model of ZAT422 alloy were established. Microstructure observation shows that when the temperature is as low as 498 K, the DRX is not completed as the true strain reaches 0.9163. However, with the temperature increasing to 648 K, the lower strain rate is more likely to result in some grains’ abnormal growth.
Key words: Mg-4Zn-2Al-2Sn alloy; hot deformation; flow stress; dynamic recrystallization
1 Introduction
Recent years, the Sn-containing magnesium alloys have received a lot of attention [1-3], for the Mg2Sn phase as the only compound formed in the Mg-Sn binary system has a high melting temperature of 1043 K, which is comparable to the precipitates in Mg-RE systems. Sn-containing magnesium alloys are believed to have the potential to become a cost-effective “RE-free” Mg-based alloy with superior heat resistance [4-6].
Studies have shown that Mg-Zn-Al-Sn alloys exhibit good tensile properties and extrudability [7-10]. According to CHEN et al [7], the addition of Sn in Mg-6Zn-2Al (mass fraction, %, same below) results in the suppression of the eutectic transformation and the refinement of divorced eutectics, and contributes to the improvement in the ambient and elevated-temperature strength. SASAKI et al [8] designed a new Mg-9.8Sn- 1.2Zn-1.0Al alloy which has good extrudability at 523 K, and the extruded alloy exhibits high yield strengths of 308 MPa in tension and 280 MPa in compression, showing a high tension to compression ratio of 0.9. CHENG et al [9] studied a similar Mg-8Sn-1Al-1Zn alloy extruded in an exit speed range of 2-10 m/min and a initial billet temperature of 523 K. As the extrusion speed increased from 2 to 10 m/min, the yield strength decreased from 244 to 199 MPa and the ultimate strength decreased from 312 to 286 MPa. CHEN et al [10] extruded the Mg-3Sn-xZn-1Al alloy at an exit speed of 4-5 m/min. With the increasing of Zn addition from 0 to 2%, the yield strength increased from 164 to185 MPa, and the ultimate tension strength increased from 250 to 290 MPa, the elongation increased from 10.8% to 12.2%. Many good results of Mg-Zn-Al-Sn alloys have been obtained. However, the deformation and dynamic recrystallization behaviors of Mg-Zn-Al-Sn alloys have been rarely studied.
In our previous work [11], a new Mg-4Zn-2Sn- 2Al (ZAT422) alloy extruded in the temperatures range of 498-648 K and exit speed of 1-2 m/min was studied. With the extrusion temperature increasing, the yield strength of the alloy decreased from 212 to 142 MPa, and the ultimate tension strength decreased from 318 to 307 MPa, the elongation decreased from 27.6% to 23.1%. Therefore, in order to have a better understanding of the hot deformation behavior of the Mg-Zn-Al-Sn alloys, the present work is focused on investigating the flow behaviors of the as-solution ZAT422 and establishing a constitutive modeling for the dynamic recrystallization (DRX) kinetics.
2 Experimental
The alloy with the chemical composition of Mg- 3.96Zn-1.92Al-1.98Sn used in the present study was prepared with high-purity Mg (>99.9%), Zn (>99.9%), Al (>99.95%) and Sn (>99.95%). The ingot specimen with the dimensions of 20 mm × 40 mm × 150 mm was obtained by melting all the metals in an electric furnace under a protective atmosphere (0.5% SF6 + 99.5% CO2, volume fraction) and then casting into a steel mould. The as-cast alloy ingot was firstly solution treated at 608 K for 4 h and 693 K for 4 h, and then machined into d8 mm × 12 mm cylindrical samples for thermal simulation experiment. The compression tests were performed with a height reduction of 60% at the temperatures of 498, 548, 598 and 648 K and the strain rates of 0.01, 0.1, 1 and 5 s-1 on a Gleeble 3800 thermo- mechanical simulator. In order to reduce interface friction, a graphite lubricant was used between the specimen and press head. Prior to being compressed, the specimens were heated to the test temperature at a heat rate of 5 K/s, followed by a holding time of 180 s. After that, the specimens were deformed to a true strain of 0.9163 and then quenched in water immediately. During the compressing process the variations of stress and strain were monitored and recorded continuously by a computer equipped with an automatic data acquisition system. The samples for observation were cut out from the longitudinally central part of the deformed specimens with the observed faces parallel to the compression direction.
3 Results and discussion
3.1 Flow behaviors
The true stress-strain curves for ZAT422 alloy are illustrated in Fig. 1, which show a classic characteristic of dynamic recrystallization [12]. First, the flow stress rapidly increases to a critical value (σc), where the dislocations piling up resulted from work hardening (WH) reaches the level of forming the nucleus of DRX grains [12]. Then, the flow stress increases slower and slower until to a peak value (σp), which shows that the flow softening caused by DRX and dynamic recovery (DRV) becomes more and more predominant, until it balanced the WH. After that, the flow stress decreases gradually to a balance state between DRX and WH. Moreover, it is also shown that the flow stress of ZAT422 alloy deformed to a certain strain decreases with the increasing of temperature or the decreasing of strain rate. The reason lies in the facts that higher temperature provides higher mobility of dislocations and lower strain rate gives longer time for the movement of dislocation, which are both beneficial for the nucleation and growth of DRXed grains or DRV [13-15].
Figure 2 shows the relation of strain rate and peak stress at a fixed temperature. It is found that the amount of peak stress change decreases with the increasing of temperature. According to the literatures [16,17], the critical resolved shear stress (CRSS) of prismatic slip system in magnesium alloy is much larger than that of basal slip at room temperature. With the increasing of temperature, the CRSS of basal slip system changes little, while the CRSS of prismatic slip system decreases rapidly until close to that of basal slip system at 548 K. Moreover, it was found in our previous work [18] that when the ZAT422 sample was deformed at 548 K, a smaller true strain can result in the occurrence of discontinuous DRX (DDRX) at 0.01 s-1. For the above reasons, the amount of peak stress change between 498 and 548 K is the largest.
Fig. 1 True stress-strain curves of ZAT422 alloy at different temperatures with strain rates of 0.01 s-1 (a), 0.1 s-1 (b), 1 s-1 (c) and 5 s-1 (d)
Fig. 2 Relation of strain rate and peak stress at fixed temperature
In order to describe the hot deformation process of the ZAT422 further, εc (the critical strain of the initiation of DRX), εp (the strain corresponding to σp) and ε* (the strain for maximum softening rate) should be determined. According to the literatures [15,19], εc for the onset of DRX can be attained when the value of |-dθ/dσ| (θ=dσ/d?, θ is strain hardening rate) reaches the minimum which corresponds to the first inflection of dσ/d? versus σ curve. And εp corresponds to the strain of θ=0 and ε* corresponds to the strain of the minimum θ. The relationships between θ and σ calculated from the true stress-strain curves of ZAT422 alloy are shown in Fig. 3. And then the values of εc/εp which can be used as a parameter reflecting the onset of DRX are obtained, as listed in Table 1. In many metals, the onset of DRX occurs at around 80% of εp, and it is also works for AZ31 alloy [20]. However, for ZAT422 alloy, the result of εc/εp=0.194-0.567 means that DRX can occur at a smaller strain, which agrees with the finding in our previous work [18].
3.2 Constitutive equations for flow behavior of ZAT422 alloy
Arrhenius equation is often used to describe the hot deformation behavior of magnesium alloy deformed at different temperatures and strain rates [15,19], which describes the relationship among strain rate 
, deformation temperature T and stress σ. And it is written as
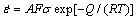(1)
where A is a material constant, Q is the hot deformation activation energy (kJ/mol), R is the mole gas constant (8.31 J/(mol·K)), and F(σ) is influenced by the stress level [15]:
(2)
where α, β, n1 and n are the material constants; α=β/n1. After substituting Eq. (2) into Eq. (1) and taking natural logarithms on both sides, Eq. (1) can be written as
(3)
(4)
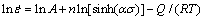(5)
The peak stress (σp) is dependent on the strain rate and the temperature T. All the σp values in the present study were already obtained from Fig. 1, and then used in the following calculation. According to Eqs. (3)-(5), when is constant, there is a linear relationship among ln , ln σp, σp and ln[sinh(ασp)], as shown in Figs. 4(a)-(c). Therefore, the material constants n1, β, α and n can be calculated from Figs. 4(a)-(c), respectively. In this study, n1, β, α and n were determined as 8.862, 0.075, 0.010 and 5.663.
Fig. 3 θ versus σ curves at different temperatures with strain rates of 0.01 s-1 (a), 0.1 s-1 (b), 1 s-1 (c) and 5 s-1 (d)
Table 1 Values of εc/εp under different deformation conditions
When is a constant, Eq. (5) can be rewritten as
(6)
As shown in Fig. 4(d), ln[sinh(ασp)] and 1/T show good linear relationship, which means that the peak stress of ZAT422 alloy deformed under the giving conditions fits the Arrhenius equation well [21]. Q and A were determined as 155.652 kJ/mol and 5.533×1012, respectively. Then, substituting A, n, α, Q and R into Eq. (1), the constitutive equation for describing the relationship among , T and σp can be expressed as
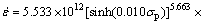
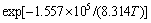(7)
3.3 Kinetics of DRX
The change of flow stress during hot deformation is attributed to the evolution of microstructure. When the flow stress increases to σc, the dislocations density reaches the level of forming the nucleus of DRX grains, and then the fraction of DRX gradually increases with the increasing of strain. Until the flow stress reaches a relatively stable value, the microstructure gets into a status in which the DRXed grains have equiaxed shape and keep constant size, and it can be believed that the DRX process have finished.
Fig. 4 Relationship among ln
, ln σp, σp, ln[sinh(ασp)] and T-1 of ZAT422 alloy
According to the Ref. [19], the kinetics of DRX can be described by the Avrami equation, which is expressed as a function of time t:
(8)
where m is the Avrami constant and k is the material constant. When the strain rate is a constant, t can be replaced by ε, and Eq. (8) can be modified as follows:
(9)
where εc and ε* under different deformation conditions have been obtained from Fig. 3, and their dependence on temperature and strain rate can be expressed as a function of Z/A (see Fig. 5):
(10)
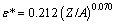(11)
where Z is the temperature compensated strain rate named the Zener-Hollomon parameter, which is expressed as follows:
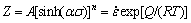(12)
In order to calculate the Avrami constant m', the solution adopted by QUAN et al [15] and KIM et al [21] is to identify the deformation condition corresponding to XDRX=1, and the criterion is the flow stress reaching a steady state and the grain size remaining stable. However, in order to solve Eq. (9), XDRX approximately equals to 0.99. As seen in Fig. 1, when the temperature is as low as 498 K, the flow stress continually decreases till the strain up to 0.9163, which means that the DRX process has not finished. Then, the deformation conditions corresponding to XDRX=0.99 are confirmed as listed in Table 2.
Fig. 5 Relationships between dimensionless parameter Z/A and εc (a) and ε* (b)
Table 2 Deformation conditions corresponding to XDRX=0.99
Substituting εc, ε* and ε0.99 into Eq. (9), the mean value of the Avrami constant m' was obtained as 1.706. Thus, the kinetic model of DRX of ZAT422 alloy can be depicted as Eq. (13):
(13)
Based on the calculation results of Eq. (13), Fig. 6 shows the predicted volume fraction of dynamic recrystallization obtained under different deformation conditions. Figure 6(a) shows that the DRX process accelerates with the increasing of temperature, and when the temperature is as low as 498 K, the DRX has not completed as the true strain reaches 0.9163. As shown in Fig. 7(a), many deformed grains still exist, which agrees with the calculation result of Eq. (13). With the temperature increasing to 598 K, completely DRXed microstructure was obtained (see Fig. 7(b)). This effect can be attributed to the increased mobility of dislocation with the increasing of temperature. As shown in Fig. 6(b), the strain required for the same amount of DRX volume fraction increases with the increasing of strain rate, that is to say, a smaller strain is required for fully recrystallization for a smaller strain rate at a certain temperature. As shown in Figs. 7(c, d), completely DRX occurs in the two samples with different strain rates. While, the DRXed grain size with 1 s-1 is more uniform compared to the sample with 0.01 s-1, this is because the DRXed grain boundaries of the sample with 0.01 s-1 having more time to glide results in some grains’ abnormal growth. And the effects of deformation condition on the operating DRXed mechanisms of ZAT422 alloy have been discussed in our another paper [18].
Fig. 6 Predicted volume fraction of dynamic recrystallization obtained at different temperatures and strain rates
4 Conclusions
1) The flow behavior of ZAT422 magnesium alloy shows a typical characteristic of dynamic recrystallization. When the deformation temperature increases from 498 to 548 K, the influence of strain rate on the peak stress is enhanced relatively.
2) The result of εc/εp=0.194-0.567 shows that the DRX of ZAT422 alloy can occur at a small strain. The activation energy of deformation is determined as 155.652 kJ/mol, and the relationships among strain, strain rate, temperature and flow stress are described as
.
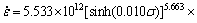
The DRX kinetic model of Mg-4Zn-2Al-2Sn alloy is established as
.
3) When the temperature is as low as 498 K, the DRX has not completed as the true strain reaches 0.9163.
Fig. 7 Microstructures of ZAT422 alloy at different deformation temperatures and strain rates
While, with the temperature increasing to 648 K, the lower strain rate is more likely to result in some grains’ abnormal growth.
References
[1] PAN H, REN Y, FU H, ZHAO H, WANG L, MENG X, QIN G. Recent developments in rare-earth free wrought magnesium alloys having high strength: A review [J]. Journal of Alloys and Compounds, 2016, 663: 321-331.
[2] GOU Jun, TANG Ai-tao, PAN Fu-sheng, SHE Jia, LUO Su-qin, YE Jun-hua, SHI Da-wei, RASHAD M. Influence of Sn addition on mechanical properties of gas tungsten arc welded AM60 Mg alloy sheets [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(8): 2051-2057.
[3] HU Guang-shan, ZHANG Ding-fei, ZHAO Ding-zang, SHEN Xia, JIANG Lu-yao, PAN Fu-sheng. Microstructures and mechanical properties of extruded and aged Mg-Zn-Mn-Sn-Y alloys [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(10): 3070-3075.
[4] LIU H M, CHEN Y G, TANG Y B, WEI S H, NIU G. The microstructure, tensile properties, and creep behavior of as-cast Mg- (1-10)%Sn alloys [J]. Journal of Alloys and Compounds, 2007, 440(1-2): 122-126.
[5] YANG Ming-bo, CHENG Liang, PAN Fu-sheng. Comparison of as-cast microstructure, tensile and creep properties for Mg-3Sn-1Ca and Mg-3Sn-2Ca magnesium alloys [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(4): 584-589.
[6] KANG D H, PARK S S, OH Y S, KIM N J. Effect of nano-particles on the creep resistance of Mg-Sn based alloys [J]. Materials Science and Engineering A, 2007, 449-451: 318-321.
[7] CHEN J H, CHEN Z H, YAN H G, ZHANG F Q, LIAO K. Effects of Sn addition on microstructure and mechanical properties of Mg-Zn-Al alloys [J]. Journal of Alloys and Compounds, 2008, 461: 209-215.
[8] SASAKI T T, YAMAMNOTO K, HONMA T, KAMADO S, HONO K. A high-strength Mg-Sn-Zn-Al alloy extruded at low temperature [J]. Scripta Materialia, 2008, 59(10): 1111-1114.
[9] CHENG W L, KIM H S, YOU B S, KOO B H, PARK S S. Strength and ductility of novel Mg-8Sn-1Al-1Zn alloys extruded at different speeds [J]. Materials Letters, 2011, 65: 1525-1527.
[10] CHEN Y, JIN L, SONG Y, LIU H, YE R. Effect of Zn on microstructure and mechanical property of Mg-3Sn-1Al alloys [J]. Materials Science and Engineering A, 2014, 612: 96-101.
[11] ZHAO Dong-qing, ZHOU Ji-xue, LIU Yun-teng, DONG Xu-guang, WANG Jing, YANG Yuan-sheng. Microstructure and mechanical properties of Mg-4Zn-2Al-2Sn alloys extruded at low temperatures [J]. Acta Metallurgica Sinica, 2014, 50(1): 41-48.
[12] BETTLES C, BARNETT M. Advances in wrought magnesium alloys [M]. Cambridge: Woodhead Publishing Limited, 2012: 186-207.
[13] YANG X Y, JI Z S, LUO G, MIURA H, SAKAI T. Dynamic recrystallization and texture development during hot deformation of magnesium alloy AZ31 [J]. Transactions of Nonferrous Metals Society of China, 2009, 19: 55-56.
[14] YUE C X, ZHANG L W, LIAO S L, PEI J B, GAO H J, JIA Y W, LIAN X J. Research on the dynamic recrystallization behavior of GCr15 steel [J]. Materials Science and Engineering A, 2009, 499: 177-181.
[15] QUAN G Z, SHI Y, WANG Y X, KANG B S, KU T W, SONG W J. Constitutive modeling for the dynamic recrystallization evolution of AZ80 magnesium alloy based on stress-strain data [J]. Materials Science and Engineering A, 2011, 528: 8051-8059.
[16] LIU Qing. Research progress on plastic deformation mechanism of Mg alloys [J]. Acta Metallurgica Sinica, 2010, 11: 1458-1472.
[17] OBARA T, YOSHINGA H, MOROZUMI S. 
Slip system in magnesium [J]. Acta Metallurgica, 1973, 21: 845-853.
[18] ZHAO D Q, YANG Y S, ZHOU J X, LIU Y, ZHAN C W. Dynamic microstructural evolution in Mg-4Zn-2Al-2Sn alloy during hot deformation [J]. Materials Science and Engineering A, 2016, 657: 393-398.
[19] LV B J, PENG J, WANG Y J, AN X Q, ZHONG L P, TANG A T, PAN F S. Dynamic recrystallization behavior and hot workability of Mg-2.0Zn-0.3Zr-0.9Y alloy by using hot compression test [J]. Materials & Design, 2014, 53: 357-365.
[20] BARNETT M R. Hot working microstructure map for magnesium AZ31 [J]. Materials Science Forum, 2003, 426: 515-520.
[21] KIM S I, LEE Y, LEE D L, YOO Y C. Modeling of AGS and recrystallized fraction of microalloyed medium carbon steel during hot deformation [J]. Materials Science and Engineering A, 2003, 355: 384-393.
Mg-4Zn-2Al-2Sn合金动态再结晶行为动力学数值模拟
赵东清1,2，杨院生1,2，周吉学1,3，刘 玉1，唐守秋1,3
1. 齐鲁工业大学(山东省科学院) 新材料研究所 山东省轻质高强金属材料重点实验室，济南 250014；
2. 中国科学院 金属研究所，沈阳 110016；
3. 齐鲁工业大学(山东省科学院) 新材料研究所 山东省汽车轻量化镁合金材料工程技术研究中心，济南 250014
摘 要：利用Gleeble 3800 热模拟试验机研究ZAT422合金在变形温度为498~648 K、应变速率为0.01~5 s-1、压下量为60%的热变形行为。基于Arrhenius方程和Avramit方程对该合金流变行为进行分析，得到变形激活能为 155.652 kJ/mol，并构建该合金的本构方程和动态再结晶模型。组织观察表明：变形温度低至 498 K，真应变为0.9163时，合金发生不完全动态再结晶；温度升高至648 K时，较低的应变速率易导致部分晶粒的异常长大。
关键词：Mg-4Zn-2Al-2Sn合金；热变形；流变应力；动态再结晶
(Edited by Xiang-qun LI)
Foundation item: Project (2016YFB0301105) supported by the National Key Research and Development Plan, China; Project (ZR2015YL007) supported by the Natural Science Foundation of Shandong Province, China; Project (ZR2015EQ019) supported by the Natural Science Foundation of Shandong Province, China
Corresponding author: Dong-qing ZHAO; Tel: +86-531-88728308; E-mail: zhaodq@sdas.org
DOI: 10.1016/S1003-6326(18)64667-9
