DOI: 10.11817/j.issn.1672-7207.2016.06.043
改进人工鱼群算法在气溶胶粒径分布反演中的应用
贺振宗,齐宏,贾腾,阮立明
(哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨,150001)
摘要:基于光谱消光法,利用一种改进的人工鱼群算法(improved artificial fish school algorithm,IAFSA)反演单峰和双峰气溶胶粒子粒径分布。其中,正问题的求解采用反常衍射近似(anomalous diffraction approximation,ADA)和Lambert-Beer定律。研究结果表明:相对标准人工鱼群算法而言,IAFSA能很好地避免出现后期收敛速度慢、精度低等问题。在非独立模型下反演气溶胶粒径分布时,IAFSA算法体现出很好的收敛精确度和鲁棒性。在非独立模型下,IAFSA算法可用于反演实际测量得到的哈尔滨地区气溶胶粒径分布。
关键词:气溶胶;改进人工鱼群算法;粒径分布
中图分类号:TP212 文献标志码:A 文章编号:1672-7207(2016)06-2141-06
Application of improved artificial fish school algorithm in retrieving aerosol particle size distribution
HE Zhenzong, QI Hong, JIA Teng, RUAN Liming
(School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: Based on the spectral extinction method, an improved artificial fish school algorithm (IAFSA) was employed to retrieve the monomodal and bimodal aerosol size distributions. The direct problem was solved by the anomalous diffraction approximation (ADA) and Lambert-beer law. The results show that IAFSA can overcome low convergence rate and accuracy, compared with AFSA. Moreover, in retrieving the aerosol size distribution with the dependent model, the IAFSA shows satisfactory convergence accuracy and robustness. IAFSA can be employed to estimate the actual aerosol size distribution over Harbin with the independent model.
Key words: aerosol; improved artificial fish school algorithm; particle size distribution
气溶胶对大气能见度、净辐射通量以及其他相关化学成分方面都有着非常深远的影响,尤其是在人们生活的地球表面,高浓度的气溶胶将会直接影响人类的身体健康。因此,为更好地了解气溶胶对人类生产生活的影响,实现在线测量大气气溶胶的特性有着重大的意义[1-2]。一般来说,气溶胶有3个极其重要的性质,即气溶胶粒径分布(particle size distribution,PSD),气溶胶光学厚度(aerosol optical depths,AODs)和埃指数( exponents)。其中,气溶胶的粒径分布对大气辐射传输和气象变化起着重要的作用。同时,气溶胶的粒径分布也被认为是一个环境质量评价标准。气溶胶对人体健康的影响从根本上取决于气溶胶颗粒的粒径,即PM[3-4]。因此,为了更好地研究大气环境对人类的影响,必须先准确地了解气溶胶粒径分布。
exponents)。其中,气溶胶的粒径分布对大气辐射传输和气象变化起着重要的作用。同时,气溶胶的粒径分布也被认为是一个环境质量评价标准。气溶胶对人体健康的影响从根本上取决于气溶胶颗粒的粒径,即PM[3-4]。因此,为了更好地研究大气环境对人类的影响,必须先准确地了解气溶胶粒径分布。
目前,虽已建立了几个研究大气气溶胶属性的全球地面气溶胶观测网络,例如AERONET和MODIS等,但如何精确地测量气溶胶的粒径分布仍是一个尚未解决的难题[5]。粗略地讲,常见的颗粒粒径测量方法主要有筛分法、沉降法、显微镜法、电感应法和光散射法等[6]。由于从粒子的散射特性中能导出气溶胶粒子粒径分布特性,光散射法结合反问题理论反演得到粒子系粒径分布的方法备受关注[6-7]。通常用于确定颗粒粒径的散射参数可以是散射光的强度或散射光强的空间分布、透射光强度相对于入射光强的衰减、散射光的偏振度等[8-9]。与其他测量方法相比,光散射法具有适用性广、粒径测量范围宽、测量速度快、仪器自动化和智能化程度高以及能够在线测量等优点。光散射测量技术可分为光谱消光法、角度散射法、衍射法及动态光谱散射法等[10-11]。其中,基于Lambert-Beer定律的光谱消光法由于只需要简单的光路设计和较少的仪器设备就能实现,因此备受广大学者的青睐[12-13]。在粒径反演时,粒子的吸收散射特性的计算关系到整个反演过程的精确性。通常来说,对于弥散颗粒辐射特性研究的主要方法有Mie理论、T矩阵(T-matrix method)、分离变量法(separation of variables method,SVM)、时域有限差分法(finite-difference time-domain,FDTD)和反常衍射近似(anomalous diffraction approximation,ADA)等[10, 14]。其中,ADA由于易于编程实现、计算精度高且适用于不同形状的粒子而受到广泛关注。TANG等[15]应用ADA算法反演了弥散粒子系粒径服从单峰和双峰分布的情况,结果表明在计算粒子的辐射特性时,ADA算法计算的结果与Mie理论以及T矩阵计算的结果吻合较好。目前,用于粒径反演的智能优化算法主要有多相微粒群算法(multi-phase particle swarm optimization algorithm,MPSO)、蚁群算法(ant colony optimization algorithm,ACO)和遗传算法(genetic algorithm,GA)等[10-11]。李晓磊[16]结合动物自治体模型,提出了人工鱼群算法(artificial fish school algorithm,AFSA),该算法是一种有效的寻优算法,具有并行简单和寻优速度快的特点。本文作者在AFSA的基础上提出了基于差分近似算法(differential evolution,DE)的改进人工鱼群算法(improved artificial fish school algorithm,IAFSA),并首次将IAFSA应用于气溶胶粒径分布的反演测量。其中,正问题的求解采用ADA和Lambert-Beer定律。基于IAFSA,首先在非独立模型下反演单峰(log-normal distribution function,L-N)和单峰Gamma分布以及双峰L-N分布。同时,进一步将IAFSA用于反演实际测量得到哈尔滨地区的气溶胶粒径分布。
1 光谱消光法
光谱消光法主要是基于Lambert-Beer定律和相关的反问题理论来求解第一类Fredholm积分方程,从而获得待测颗粒系的粒径分布。根据Lambert-Beer定律,当一束波长为λ光强为I的平行光穿过弥散粒子系时,若弥散粒子系的光学厚度薄且独立散射占优时,光谱辐射强度沿着原光路按指数规律衰减,即[8, 10]
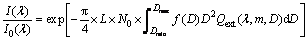 (1)
(1)
式中: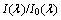 为光谱透射率,通常通过实验测得;I0(λ)为入射激光强度;I(λ)为透射激光强度;λ为波长;L为弥散粒子系的几何厚度,m;Dmax和Dmin分别为积分的上下限;N0为整个粒子系单位体积内的数密度;f(D)为粒子系的粒径分布函数;Qext为粒子的光谱衰减因子,为粒子的复折射率m、入射激光的波长λ以及粒子粒径D的函数。本研究应用ADA计算粒子的光谱衰减因子,其表达式[12]为
为光谱透射率,通常通过实验测得;I0(λ)为入射激光强度;I(λ)为透射激光强度;λ为波长;L为弥散粒子系的几何厚度,m;Dmax和Dmin分别为积分的上下限;N0为整个粒子系单位体积内的数密度;f(D)为粒子系的粒径分布函数;Qext为粒子的光谱衰减因子,为粒子的复折射率m、入射激光的波长λ以及粒子粒径D的函数。本研究应用ADA计算粒子的光谱衰减因子,其表达式[12]为
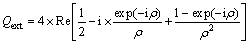 (2)
(2)
式中: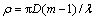 ;i为虚数单位;Re表示虚数实部。
;i为虚数单位;Re表示虚数实部。
2 人工鱼群算法
在一片水域中,鱼群能通过自行或尾随其他鱼群来找到营养物质多的地方,所以通常鱼生存数目最多的地方一般就是水域中营养物质最多的地方。人工鱼群算法就是依据鱼群的这些特点而提出。人工鱼群算法包括4个算子:随机行为、觅食行为、聚群行为和追尾行为[16-17]。鱼群中的个体所处的状态即为待求解向量,通过鱼群中个体鱼之间的协作,从而实现对问题的求解。此外,在算法中通常设置1个公告板,用于记录鱼群中当前最优个体状态。
2.1 标准的人工鱼群算法
设人工鱼个体i的当前状态可以表示为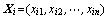 (Xi为矢量),鱼群所处位置的食物浓度设为
(Xi为矢量),鱼群所处位置的食物浓度设为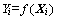 ,即求解的目标函数,鱼群个体之间的距离表示为
,即求解的目标函数,鱼群个体之间的距离表示为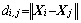 ,V为鱼的视野范围,δ为拥挤因子,S为鱼群移动步长,N为觅食行为中重复尝试次数。人工鱼群算法流程如下[16-17]。
,V为鱼的视野范围,δ为拥挤因子,S为鱼群移动步长,N为觅食行为中重复尝试次数。人工鱼群算法流程如下[16-17]。
1) 觅食行为。设鱼群的当前状态为Xi,在其视野范围V内(即di,j<V)随机选择1个新状态Xj,如式(3)所示。若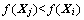 ,则鱼按式(4)向该状态移动一步;否则,重新选择1个新的Xj,进行尝试。尝试N次后仍不能移动,则将鱼随机移动1步,R1和R2为0~1之间的随机数。
,则鱼按式(4)向该状态移动一步;否则,重新选择1个新的Xj,进行尝试。尝试N次后仍不能移动,则将鱼随机移动1步,R1和R2为0~1之间的随机数。
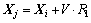 (3)
(3)
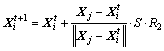 (4)
(4)
2) 聚群行为。设鱼的当前状态为Xi,在其视野范围V内搜索聚集鱼群的伙伴数目nf以及中心位置Xc,Yc为中心位置浓度食物。若Yc/nf>δYi,则表示该中心位置不拥挤且有较多食物,鱼将向该方向前进一步,如下式所示:
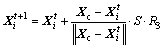 (5)
(5)
否则执行觅食行为,R3为0到1之间的随机数。
3) 追尾行为。设鱼的当前状态为Xi,在其视野范围内搜索伙伴中Yj为最大值的伙伴Xj。若Yj/nf>δYi,则表明伙伴Xj的状态有较高的食物浓度并且周围不太拥挤,鱼将向该位置前进一步,否则继续觅食行为。
4) 更新公告板。设1个公告板,用于记录鱼群内历史最佳鱼的状态Xbest。各人工鱼每迭代一次都检查自身状态,如果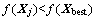 ,则将Xbest修改为Xi。
,则将Xbest修改为Xi。
5) 随机行为。设鱼的当前状态为Xi,在没有执行其他任何行为时,鱼群在自己视野范围V内随机游动。
2.2 融合差分近似演化的改进人工鱼群算法
差分近似算法是由STORN等[18]提出的一类求解连续全局优化问题的演化算法,其基本思想是通过突变、交叉和进化产生新的个体的方式来实现。其中,突变是把种群中2个个体的向量差加权后按照一定的规则与第3个个体求和来产生新个体。然后,交叉将产生的新个体与靶个体结合产生试探个体Xi,mut=(xi1,mut,xi2,mut,…,xin,mut),即
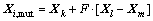 (6)
(6)
最后,比较产生的试探个体、靶个体以及当前公告板记录最优个体的目标函数。若新个体的目标值比当前最优个体的目标函数的高,则新产生个体取代当前最佳个体,否则当前最优个体仍保存下来,如下式所示[18]:
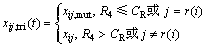 (7)
(7)
式中:F为取值在[0,2]之间的突变因子;i,k,l和m表示鱼群中不同的个体;xij,tri为第i个粒子在第j维问题上所选择的最优位置;CR为取值在[0,1]之间的交叉因子;r(i)为随机选择的鱼群个体。融合差分近似演化的人工鱼群算法流程如下。
1) 初始化人工鱼群规模、视野范围V、步长、最大重复尝试次数N以及最大迭代次数等。
2) 计算鱼群个体的目标函数,并将其目标函数与公告板进行比较,若较好,则将其赋予公告板。
3) 鱼群进行觅食、群聚以及追尾行为。
4) 计算比较3种行为的目标函数,选择最优值。
5) 在步骤4)选择的最优值的基础上进行差分近似,并将试探个体、靶个体的目标函数和公告板比较。若较好,则将其赋给公告板,同时更新相应的最佳鱼的状态Xbest。
6) 检查终止条件(通常为达到预定进化次数或足够好的适应值)。若满足终止条件,则输出最优解(公告板中人工鱼状态和函数值),算法终止,否则,转至步骤3)。
3 数值模拟
通常在反演气溶胶粒径分布时,根据气溶胶粒径分布的函数类型是否事先已知,可以将粒径分布反演分为2种类型:若事先已知粒径分布函数,则为非独立模型;否则为独立模型。基于IAFSA,本文首先研究了单峰L-N分布、单峰Gamma分布及双峰L-N分布在非独立模型下的反演,其分布函数分别为fL-N(D),fGamma(D)和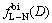 。3种气溶胶粒子分布函数表达式为[4, 8]:
。3种气溶胶粒子分布函数表达式为[4, 8]:
 (8)
(8)
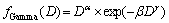 (9)
(9)

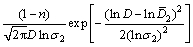 (10)
(10)
式中:在L-N分布中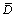 ,
,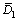 和
和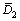 为分布函数的特征参数;σ,σ1和σ2为分布参数;n为双峰函数的权重;在Gamma分布中,通常来说γ=1,所以,只有α和β需要通过反演得到。
为分布函数的特征参数;σ,σ1和σ2为分布参数;n为双峰函数的权重;在Gamma分布中,通常来说γ=1,所以,只有α和β需要通过反演得到。
在本研究中,气溶胶粒子的复折射率假设为m=1.53+0.05i(i为虚部单位)。为简单起见,不考虑粒子的复折射率随着波长的变化。根据前期的研究可知,增加实验测量的波长数目,可以提高反演结果的精确度,但同时会增加计算时间[10]。因此,综合考虑计算时间和反演精度,本研究实验测量的波长设为λ=0.45,0.55,0.65 μm。假设粒子系的尺寸范围为常见粒子的直径测量范围,即0.01~10 μm。气溶胶粒子的粒径分布真值如表1所示。
表1 气溶胶粒子粒径分布真值
Table 1 True values of aerosol particle size distribution

在反问题研究中,通常依据目标函数值来判断反演过程是否收敛。在本研究中,目标函数Fobj为测量的光谱透射率和反演的光谱透射率比值的均方差,其表达式为
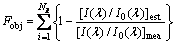 (11)
(11)
式中:Nλ为实验测量波长,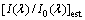 为仿真估计的透射率;
为仿真估计的透射率;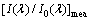 为实际测量的透射率。考虑到IAFSA是随机优化且具有一定统计误差的算法,因此,所有模拟计算结果取50次计算的平均值。此外,本文还采用粒径分布的相对偏差ε来评价反演结果的优劣。ε表示粒径分布的反演结果和真实分布之间在每个小分布区间内的偏差的累积和,其表达式为
为实际测量的透射率。考虑到IAFSA是随机优化且具有一定统计误差的算法,因此,所有模拟计算结果取50次计算的平均值。此外,本文还采用粒径分布的相对偏差ε来评价反演结果的优劣。ε表示粒径分布的反演结果和真实分布之间在每个小分布区间内的偏差的累积和,其表达式为
 (12)
(12)
式中:N为粒径分布区间[Dmax,Dmin]所划分的份数;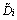 表示第i区间[Di,Di+1]的中间值;
表示第i区间[Di,Di+1]的中间值;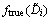 为第i区间[Di,Di+1]的真实分布值;
为第i区间[Di,Di+1]的真实分布值;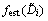 为第i区间[Di,Di+1]的反演分布值。由式(12)可以看出:δ越小,反演的精度越高。
为第i区间[Di,Di+1]的反演分布值。由式(12)可以看出:δ越小,反演的精度越高。
图1所示为AFSA和IAFSA在反演单峰L-N分布时的目标函数值随着迭代次数增加的变化情况,其控制参数如表2所示。其中,判断反演过程结束的依据迭代次数到达1 000或目标函数值小于收敛精度10-16。从图1可以看出:与AFSA相比,IAFSA能在较短的时间和较少的迭代次数内得到较小的目标函数值,即IAFSA收敛速度快并且收敛精度高。因此,在以下研究中均采用IAFSA来反演在不同随机测量误差η下的气溶胶粒径分布。
单峰气溶胶L-N和Gamma分布的反演结果如表3所示,相应的反演曲线如图2和图3所示。由表3、图2和图3可以发现:当反演单峰L-N分布时,即使在随机误差为5%的情况下,改进的人工鱼群算法也能反演得到很好的结果。而对于单峰Gamma分布,在无随机测量误差的情况下,反演结果很理想,但随着测量误差的增加,反演结果误差逐渐越大。双峰气溶胶L-N分布反演结果如表4和图4所示。从表4和图4可以看出:反演曲线中主峰的反演值和真实的气溶胶粒径分布吻合很好,而副峰的反演误差随着测量误差的增加而逐渐增大。但总体而言,可以认为IAFSA是一种在非独立模型下能很好地反演气溶胶粒径分布的反问题优化算法。
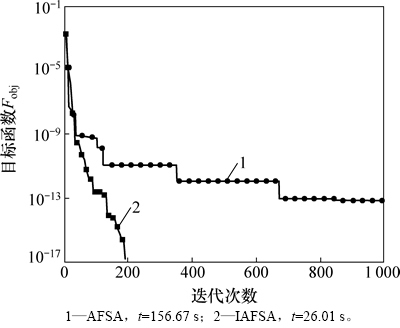
图1 AFSA和IAFSA的目标函数比较
Fig. 1 Comparison of objective function values of AFSA and IAFSA
表2 人工鱼群算法控制参数
Table 2 The control parameters of the AFSA and IAFSA
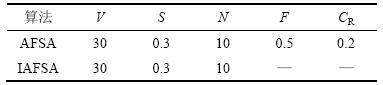
表3 2种常见单峰气溶胶粒径分布函数的反演结果
Table 3 Inverse results of two kinds of common monomodal aerosol particle size distributions
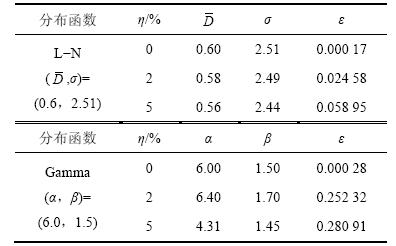
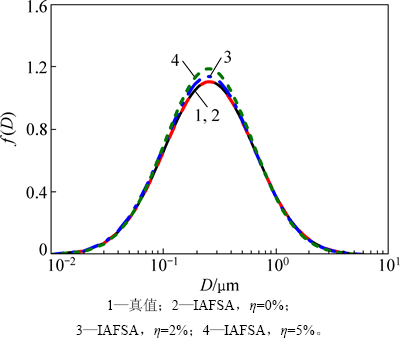
图2 基于IAFSA的单峰L-N分布反演结果
Fig. 2 Inverse results of monomodal L-N distribution by IAFSA
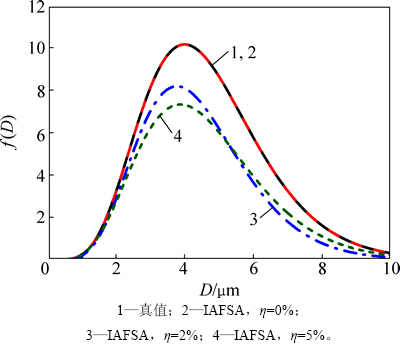
图3 基于IAFSA的单峰Gamma分布反演结果
Fig. 3 Inverse results of monomodal Gamma distribution by IAFSA
表4 双峰气溶胶分布函数的反演结果
Table 4 Inverse results of bimodal aerosol particle size distribution
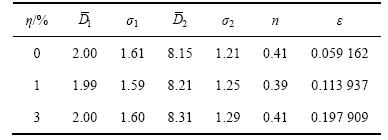
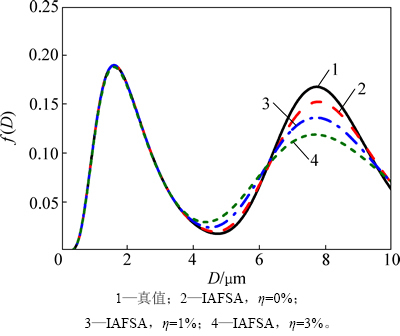
图4 基于IAFSA的双峰L-N分布反演结果
Fig. 4 Inverse results of bimodal L-N distribution by IAFSA
4 实验研究
基于IAFSA算法,研究实际测量的气溶胶的粒径分布反演情况。图5所示为2014-05-06在哈尔滨工业大学测量得到的单峰气溶胶粒子的粒径分布情况。由于事先不知道该气溶胶粒子粒径分布的函数类型(即在独立模型下),所以采用一般性的单峰分布函数Johnson’s-SB (J-SB)函数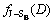 和修正的β(M-β)函数
和修正的β(M-β)函数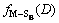 来近似地模拟实际测量的气溶胶粒径分布。这2种一般性函数的表达式[12]为
来近似地模拟实际测量的气溶胶粒径分布。这2种一般性函数的表达式[12]为

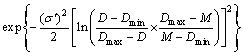 (13)
(13)
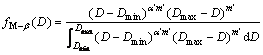 (14)
(14)
式中:σ′,M,α′和m′为特征常数。
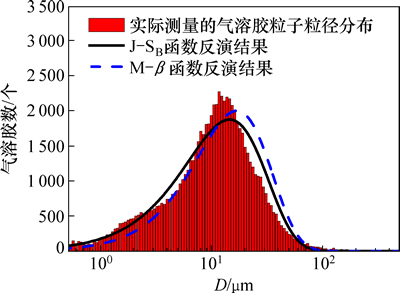
图5 基于IAFSA的双峰L-N分布反演结果
Fig. 5 Inverse results of bimodal L-N distribution by IAFSA
从图5可以看出:在实验测量不可避免地存在测量误差的情况下,IAFSA能够很好地反演实际测量的单峰气溶胶的粒径分布,同时单峰J-SB函数和M-β函数也被证明能作为一种很好的分布函数来近似地模拟实际单峰气溶胶粒子的粒径分布情况。
5 结论
1) 改进的人工鱼群算法能很好地避免出现标准人工鱼群算法后期收敛速度慢、精度低等问题。
2) 在无随机测量误差情况下,改进人工鱼群算法体现出很好的反演精度,而随着测量误差的增加,单峰Gamma分布反演结果的精度不断地下降,而单峰和双峰L-N分布的反演结果相对令人满意。
3) 在实际测量的单峰气溶胶粒子粒径分布的反演中,IAFSA同样具有较合理的反演精度。此外,J-SB函数和M-β函数也被证明可作为一种假设的分布函数在单峰气溶胶粒径分布函数未知时来近似地模拟气溶胶粒子粒径分布。
4) IAFSA在研究气溶胶粒子粒径分布方面仍然体现出较大的潜力,是一种很好的研究粒径分布的反问题方法。未来的研究将会进一步尝试将IAFSA应用于非球形气溶胶粒子粒径分布的反演。
参考文献:
[1] FRANSSENS G, DE-MAZIΝRE M, FONTEYN D. Determination of the aerosol size distribution by analytic inversion of the extinction spectrum in the complex anomalous diffraction approximation[J]. Applied Optics, 2000, 39(24): 4214-4231.
[2] RUAN Liming, WANG Xiying, QI Hong, et al. Experimental investigation on optical constants of aerosol particles[J]. Journal of Aerosol Science, 2011, 42(11): 759-770.
[3] GONG Wei, ZHANG Shanshan, MA Yingying. Aerosol optical properties and determination of aerosol size distribution in Wuhan, China[J]. Atmosphere, 2014, 5(1): 81-91.
[4] LENOBLE J, REMER L, TANRE D. Aerosol remote sensing[M]. Chichester: Springer, 2013: 1-15.
[5] KOKHANOVSKY A A, LEEUW G H. Satellite aerosol remote sensing over land[M]. Chichester: Springer, 2009: 5-20.
[6] 唐红. 光全散射法颗粒粒径分布反演算法的研究[D]. 哈尔滨: 哈尔滨工业大学仪器科学与技术学院, 2008: 1-12.
TANG Hong. Study of inversion algorithm of particle size distribution using total light scattering method[D]. Harbin: Harbin Institute of Technology. Instrumentation Science and Technology, 2008: 1-12.
[7] 王丽, 孙晓刚. 基于模式搜索的光谱消光粒径分布反演算法的研究[J]. 光谱学与光谱分析, 2013, 33(3): 618-622.
WANG Li, SUN Xiaogang. Research on pattern search method for inversion of particle size distribution in spectral extinction technique[J]. Spectroscopy and Spectral Analysis, 2013, 33(3): 618-622.
[8] 蔡小舒, 苏明旭, 沈建琪. 颗粒粒度测量技术及应用[M]. 北京: 化学工业出版社, 2010: 3-15.
CAI Xiaoshu, SU Mingxu, SHEN Jiangqi. Particle size measurement techniques and applications[M]. Beijing: Chemical Industry Press, 2010: 3-15.
[9] 陈庭将. 光散射法在颗粒测量技术中的应用[D]. 西安: 西安电子科技大学物理与光电工程学院, 2011: 9-17.
CHEN Tingjiang, The application of light scattering method in particle measuring technique[D]. Xi’an: Xidian University. School of Physics and Optoelectronic Engineering, 2011: 9-17.
[10] HE Zhenzong, QI Hong, YAO Yuchen, et al. An effective inversion algorithm for retrieving bimodal aerosol particle size distribution from spectral extinction data[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2014, 149: 117-127.
[11] QI Hong, ZHANG Biao, REN Yaotao, et al. Retrieval of spherical particle size distribution using ant colony optimization algorithm[J]. Chinese Optics Letters, 2013, 11(11): 112901(1-5).
[12] HE Zhenzong, QI Hong, WANG Yuqing, et al. Inverse estimation of the spheroidal particle size distribution using ant colony optimization algorithms in multispectral extinction technique[J]. Optics Communications, 2014, 328(10): 8-22.
[13] QIN Shouxuan, CAI Xiaoshu. Indirect measurement of the intensity of incident light by the light transmission fluctuation method[J]. Optics Letters, 2011, 36(20): 4068-4070.
[14] CHEN Xiaozhen, ZHOU Wu, CAI Xiaoshu, et al. In-line imaging measurements of particle size, velocity and concentration in a particulate two-phase flow[J]. Particuology, 2014, 13(1): 106-113.
[15] TANG Hong, LIN Jianzhong. Retrieval of spheroid particle size distribution from spectral extinction data in the independent mode using PCA approach[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2012, 115: 78-92.
[16] 李晓磊. 一种新型的智能优化方法-人工鱼群算法[D]. 杭州: 浙江大学信息科学与工程学院, 2003: 22-32.
LI Xiaolei. A new intelligent optimization method-artificial fish school algorithm[D]. Hangzhou: Zhejiang University. Institute of Systems Engineering, 2003: 22-32.
[17] 聂黎明. 人工鱼群算法及其应用[D]. 南宁: 广西民族大学数学与计算机科学学院, 2009: 8-15.
NIE Liming. Artificial fish school algorithm and its application[D]. Nanning: Guangxi University for Nationalities. School of Mathematics and Computer Science, 2009: 8-15.
[18] STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
(编辑 刘锦伟)
收稿日期:2015-06-09;修回日期:2015-08-21
基金项目(Foundation item):国家自然科学基金资助项目(51476043);中国民航大学天津市民用航空器适航与维修重点实验室开放基金资助项目;哈尔滨市科技创新人才研究专项基金资助项目(2014RFQXJ047)(Project(51476043) supported by the National Natural Science Foundation of China; Project supported by the Fund of Tianjin Key Laboratory of Civil Aircraft Airworthiness and Maintenance in CAUC; Project (2014RFQXJ047) supported by the Technological Innovation Talent Research Special Fundation of Harbin)
通信作者:齐宏,教授,博士生导师,从事热辐射传输及辐射物性研究;E-mail:qihong@hit.edu.cn