预焙铝电解槽三维槽帮形状的模拟计算
崔喜风,邹忠,张红亮,李劼,徐宇杰
(中南大学 冶金科学与工程学院,湖南 长沙,410083)
摘要:应用APDL语言设计一种新型的三维槽帮形状计算算法,通过循环调用前处理、求解和后处理模块,自动调整三维槽帮表面节点坐标,实现铝电解槽三维槽帮形状的计算。选择成熟的180 kA铝电解槽作为研究算例,在有限元软件ANSYS的平台上建立四分之一槽电热模型,并引入热接触来描述熔体与槽帮、阳极和阴极等之间的对流传热,进行三维槽帮的数值仿真研究。采用这种三维计算方法可以更加真实的考虑铝电解槽的结构和工艺参数情况,电热耦合计算又将电场对热场的影响考虑在内,更加符合实际情况。研究结果表明:该算法得到的槽帮形状与实测结果基本一致,同时验证铝电解槽槽帮在小面厚度大于大面厚度,而在角部处槽帮最厚的规律。该方法可为新型铝电解槽设计提供技术支撑。
关键词:铝电解槽;3D槽膛内形;电热耦合计算;热接触;有限元
中图分类号:TF821 文献标志码:A 文章编号:1672-7207(2012)03-0815-06
Simulation calculation of 3D freeze profile in prebaked aluminum reduction cells
CUI Xi-feng, ZOU Zhong, ZHANG Hong-liang, LI Jie, XU Yu-jie
(School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The APDL was used to loop through the PREP7, SOLUTION and POST1 modules, so as to relocate the nodes on the surface of the freeze. Then, the 3D calculation for the side-ledge profile was fulfilled. Taking a 180 kA aluminum electrolysis cell as the numerical example, based on ANSYS, the quarter thermal-electric model was developed, and the thermal conductance contact from the melt to the frozen electrolyte, the anodes and bottom cathodes was introduced in order to express the corresponding thermal convection. More dimensional information was included in the 3D-1/4 cell model, and influences of electric were considered because it was thermal-electric coupled field calculation, both of which made this calculation method closer to the real situation. The results show that the 3D frozen profile obtained agrees very well with practical situation, and the frozen electrolyte of the endwall is thicker than that of the sidewall, and the corner has the thickest side ledge. This computation method can be used to guide the design of developing cell structure.
Key words: aluminum reduction cell; 3D side wall freeze profile; thermal-electric coupled field calculation; thermal conductance contact; finite element
铝电解槽的槽帮位于槽膛内壁上,保护侧部炭块免受电解质和铝液等高温熔体的侵蚀,同时,适当的槽帮厚度能够保持电解过程的热平衡和物料平衡,通过槽帮的溶解与生成,降低铝电解生产的温度波动和浓度波动。当槽温升高时, 槽帮减薄增强散热,阻止槽温的升高;当槽温降低时,槽帮增厚,阻止热量散失,并多发阳极效应以提高温度。同时,当Al2O3浓度下降时,槽帮溶解增加电解质的浓度;当Al2O3浓度升高时,沉淀增多, 槽帮增厚阻止Al2O3 浓度的过饱和[1]。良好的铝电解槽保温结构设计是形成理想槽帮形状的前提条件。顶部、侧部和底部的保温情况决定了铝电解槽的温度分布以及槽帮厚度和伸腿长度。极距、阳极缝宽以及换极操作等都无疑也会影响到槽帮形状。因此,对槽帮形状受这些参数的影响程度的研究,对于铝电解槽的结构设计以及处理生产过程中出现的各种问题,具有重要的指导作用。而不断优化的铝电解槽槽帮形状计算方法,对于这些研究具有非常重要的意义。对铝电解槽的温度场以及槽帮形状的计算,前人已经提出了各种计算模型。Haupin[2]提出了采用一维热流管模型计算铝电解槽槽帮厚度,一维模型简单、计算速度快,但计算结果比较粗糙,与实际情况相差较大。目前,随着计算机软硬件技术的不断进步,铝电解槽的二维和三维电热耦合计算逐渐成为可能[3-5]。然而,对于槽帮形状的计算虽然已有很多的文献报道,但都局限在一维或二维的热计算,没有反映出电场的影响以及大面、小面和角部槽帮厚度的差异[2, 6-9]。基于大型有限元软件ANSYS计算平台,本文作者开发了计算三维槽帮形状的四分之一铝电解槽电热耦合模型,设计了三维槽帮的计算算法,成功得到三维槽帮形状分布,通过与实测值的比较,验证了该算法的准确性,并较具体的描述了槽帮形状沿大面、小面和角部方向的变化趋势。
1 三维槽帮形状算法描述
1.1 程序基本步骤
通过APDL语言,循环调用ANSYS中的前处理、求解和后处理模块,根据槽帮表面节点温度重新确定其坐标值,直至最终得到节点温度在设定误差范围内的槽帮形状。其主要运行步骤如下:
(1) 假设初始槽帮形状,建立四分之一铝电解槽模型,并进行电热场耦合计算,得到铝电解槽温度分布情况;
(2) 进行后处理,检验槽帮内表面节点温度是否在电解质结晶和熔化的温度范围内;
(3) 如果所有节点均已满足所设定的温度误差,则退出;否则根据计算得到的节点温度值重新确定节点坐标;
(4) 由计算得到的槽帮形状,建立新的铝电解槽模型,并重新加载计算;
(5) 重复步骤(2)~(4),直至所有节点均在设定的温度误差范围内,或者运行达到了指定的运算次数为止。程序运行流程图如图1所示。
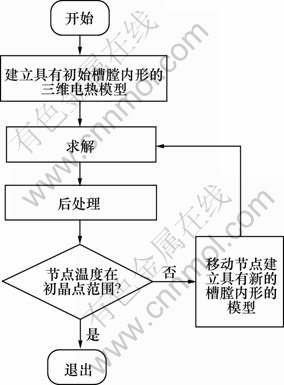
图1 程序运行流程图
Fig.1 Flow chart of program
1.2 节点坐标计算
每次循环结束,需进行后处理计算新的槽帮形状。槽帮形状的变化,主要是其厚度的变化,所以,只是节点水平方向坐标发生改变,而z保持不变。对于图1所建立的模型,小面的节点只改变x,大面的节点只改变y,其他坐标值均保持不变。
为计算节点坐标变化幅度,参考Li等[8]所提出的节点移动策略,定义一个专门的节点移动步长Lstep,根据不同节点温度高于或者低于结晶温度的程度,其坐标的变化也各不相同。对于本次计算所建立的模型,其小面和大面的节点坐标变化如下式所示:
 (1)
(1)
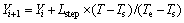 (2)
(2)
其中:Xi+1和Yi+1为计算得到的坐标;Xi和Yi为初始坐标;T为节点温度;Ts和Te分别为结晶温度和熔体温度。当节点温度比结晶温度高时,槽帮熔化变薄,小面x减小,大面y增大;反之,熔体凝固槽帮变厚。
1.3 仿真基本过程
(1) 计算给定槽帮形状下铝电解槽的温度分布 情况。
(2) 在槽帮内表面选取一系列的节点,读取其温度值,计算相应移动后节点的坐标值。其中,小面内表面节点x代入式(1),y和z保持不变;大面内表面节点y代入式(2),x和z保持不变。
(3) 根据计算得到的节点得到新的槽膛内形,并重新建立模型。
(4) 在新模型上加载边界条件并计算其温度分布和槽膛内表面节点温度。
(5) 当所有节点温度满足要求时,结束计算。
2 算例计算模型描述
2.1 材料属性的定义
铝电解槽内衬结构包括多种保温和耐火材料,整个槽的温度变化范围也很大(100~970 ℃)[10],采用ANSYS结构化设计语言(APDL)用参数来定义各个材料的属性,主要是热导率和电导率随着温度的非线性变化,实现铝电解槽电热场的非线性计算。铝液和电解质熔体的实际热导率分别为1.69 W/(m·℃)和77.95 W/(m·℃),但在电磁力以及气泡搅拌力作用下,熔体作复杂的流动,因此,均取较大的热导率实现熔体的等温。铝液部分垂直方向流速较小,仍取实际热导率77.95 W/(m·℃)。
2.2 算例几何模型及网格划分
180 kA级预焙铝电解槽为我国自行设计并全面推广过的一种成熟槽型,具有现行大型预焙铝电解槽的所有结构特征,同时模型较小,方便建模计算,节约花费在建模和网格划分等方面的精力以及计算时间,是用于研究较好的算例选择。考虑到铝电解槽结构的复杂性和对称性,本文建立了四分之一槽模型,并进行了相应的简化。在实际铝电解生产过程中,炭阳极逐渐消耗,要按照一定的周期更换阳极,因此阳极高度参差不齐。为了简化模型,定义计算得到的平均值350 mm为阳极高度。与二维模型相比,此模型包含更多的尺寸参数,更加接近实际情况,并且电流对槽帮的影响也在模型的考虑范围内。
图2所示为所建立算例模型的网格划分图。模型包括:阳极导杆和钢爪、阳极、电解质熔体、铝液、阴极和钢棒等导电部分,用具有电热2个自由度的SOLID69单元进行网格划分;氧化铝覆盖料、电解质结壳、侧部炭块、槽帮伸腿、底部保温材料以及槽壳等不导电部分用仅有一个温度自由度的SOLID70单元进行网格划分。在电接触和热接触的定义中,采用接触对单元CONTA173和TARGE170。
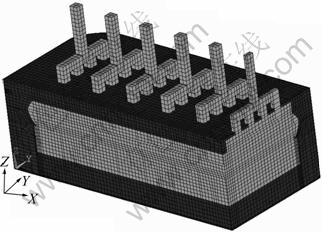
图2 模型网格划分图
Fig.2 Sketch of model mesh
2.3 初始边界条件
电流自阳极流入电解槽,流经电解质熔体和铝液,再由阴极炭块和钢棒流出。由于电流强度高,各导电部分特别是电解质熔体产生大量热,再通过电解槽外表面与外部空气的热对流和热辐射作用将热量散失。其电场和热场计算的边界条件如下:
(1) 在阳极导杆上施加相应进电比大小的电流,阴极钢棒端部施加零电位。
(2) 以各导电部分特别是电解质产生的焦耳热为热源,并适当校核电解质的电阻率,以考虑阳极气泡以及氧化铝溶解对电热场的影响;将热辐射作用等量转化为热对流,取综合换热系数,仅定义槽壳表面与外界的对流换热作为热损失。
2.4 电热场控制方程
铝电解槽中的电场问题满足欧姆定律和电流守恒定律:
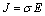 (3)
(3)
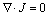 (4)
(4)
式中:J为电流密度;E为电场强度;σ为电导率。根据电场计算的控制方程:
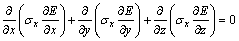 (5)
(5)
可获得标量电势φ与电场强度E之间的关系 ,即可求得铝电解槽的电场分布情况。
,即可求得铝电解槽的电场分布情况。
很多学者对阴极电压降进行了相关的现场测量和实验室研究[11-12],研究表明:阴极钢棒与阴极炭块间的接触电压在阴极压降中占有较大比例,该部分的电接触分析对整个铝电解槽的电场计算非常必要。所以定义阴极参考与阴极钢棒之间的电接触,为了保证这一部分温度场的连续性,采用热约束方程实现两部分的连接。
铝电解槽热场稳态计算的控制方程为:
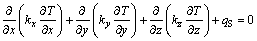 (6)
(6)
式中:T为温度;k为导热系数;qS为热源强度,对于导电部分等于控制单元的焦耳热,对于非导电部分等于0。通过电场产生的焦耳热将电场和热场耦合起来进行计算。
2.5 热接触
槽帮表面即电解质的初晶温度约为935 ℃,与其接触的电解质温度高达950 ℃,在仿真计算中多采用热对流的方式来描述槽帮表面的热量传递:
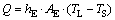 (7)
(7)
其中:Q为对流传热量;hE为熔体与槽帮之间的对流传热系数;AE为接触面积;TL为环境温度,即熔体温度;TS为槽帮内表面温度即电解质结晶温度,取935 ℃。但对于本文的电热耦合计算,熔体温度由电热场计算所产生的焦耳热来决定并非取定值950 ℃,不能用这个方法来描述此热量传递。
一般认为,稳态条件下,在高温熔体与凝固槽帮之间存在一层含Al2O3较高的黏稠过渡层[13] ,这一区域的电解质成分不同于槽内电解质, 且有较大的温度梯度。本次计算中,通过在熔体与槽帮之间定义热接触描述这一黏滞层的方式来描述槽帮表面与内部熔体之间的热量传递,式(7)可描述为:
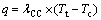 (8)
(8)
其中:q为热流密度,即单位面积传递的热量; 为接触面的接触热导率,相当于式(8)中的hE,取相同的值并具有相同的单位。Tt和Tc分别为目标面和接触面的温度。定义接触时,定义熔体面为目标面,槽帮伸腿表面为接触面,分别采用目标单元TARGE170和接触单元CONTA173,选择接触自由度为热接触。
为接触面的接触热导率,相当于式(8)中的hE,取相同的值并具有相同的单位。Tt和Tc分别为目标面和接触面的温度。定义接触时,定义熔体面为目标面,槽帮伸腿表面为接触面,分别采用目标单元TARGE170和接触单元CONTA173,选择接触自由度为热接触。
熔体与阳极和阴极之间也是通过对流换热进行热量传递,有一定的温度梯度存在。在本文的计算中,均应用热接触取代热对流。定义接触时,定义熔体面为目标面,阳极和阴极表面为接触面,分别采用目标单元TARGET170和接触单元CONTACT173。由于二者之间除了热量传递,还有电流通过,因此,选择接触自由度为电-热接触,并取较大的接触电导率实现接触面的等电位。
3 结果讨论与分析
经过多次的循环计算,得到最终的槽帮形状。图3所示为具有最终槽帮形状的铝电解槽温度分布云图。由图3可以看出:该计算结果等温线分布合理,900 ℃等温线在阴极炭块层以下,保证了阴极炭块温度高于900 ℃,避免电解质在阴极炭块中结晶,造成炭块的损坏;800 ℃等温线在保温砖层以上,保证了保温砖温度在800 ℃等温线以下,以免保温砖受高温作用而破坏。
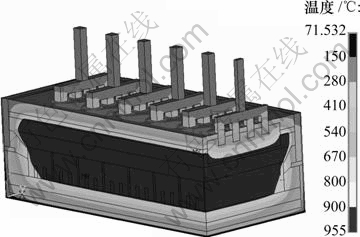
图3 铝电解槽温度分布云图
Fig.3 Temperature profile of quarter cell
图4所示为熔体温度分布云图。电解质等温温度为952.3 ℃,过热度为17 ℃。铝液自上至下温度逐渐降低,其平均温度与电解质相差4 ℃左右,与实测[14]相吻合。此时,将槽周围散热量及其所占比例列于 表1。这与典型预焙阳极电解槽热损失的分配要求相一致[15]。
图5所示为计算所得3D槽帮形状示意图。由图5可以看出:槽帮在小面比大面厚,而在角部处最厚。
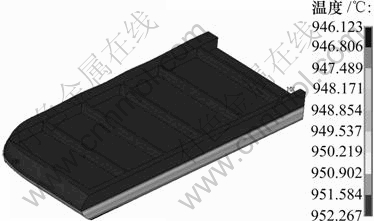
图4 铝电解槽温度分布云图
Fig.4 Temperature distribution of melt
表1 铝电解槽周围散热分布
Table 1 Heat dissipation distribution of aluminum reduction cell

为了清楚地揭示三维槽帮的形状演变规律,将小面拉伸至与大面平齐,如图6所示,大面Ll=3.775 m,取11节点,小面LS=1.555 m,取5节点,使大面和小面处于同一坐标系中,小面端点作为0坐标点。提取槽帮最薄处的槽帮厚度,作图如图7所示。
从图7可以看出:(1) 小面槽帮比大面的厚;(2) 无论是大面还是小面,自中间至角部,槽帮逐渐变厚,
但变化幅度比较小;(3) 在靠近角部处槽帮厚度有大幅度增加,这说明小面和角部处的保温效果不好。在实际生产过程中,端部阳极与中间阳极相比,产热量相同,但散热面积却大了很多,特别是角部拐角处,有较大的散热面积。因此,小面和角部的散热量大,因此,现行传统槽的设计原则是小面和角部保温而大面散热,说明计算结果是比较符合实际情况的。
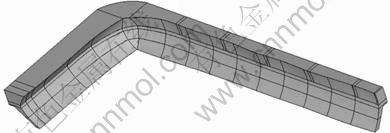
图5 3D槽帮形状示意图
Fig.5 3D profile of side ledge
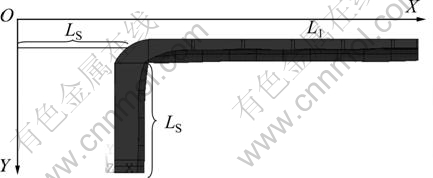
图6 槽帮节点分布示意图
Fig.6 Schematic of node distribution
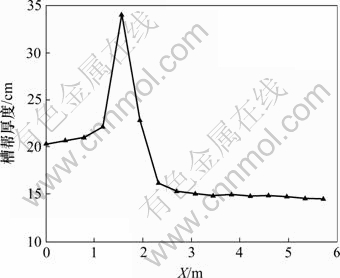
图7 槽帮厚度-x分布曲线
Fig.7 Thickness-x curve of typical nodes
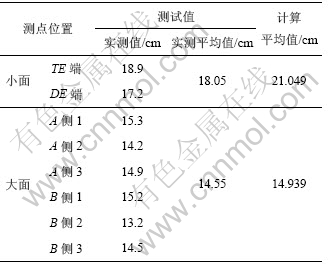
同时,为了验证计算模型的准确性,将槽膛内形参数计算值与某铝厂同规格预焙铝电解槽系列204号电解槽测试值进行了对比,结果如表2所示。由于角部槽帮厚度与大小面差异大,在求计算平均值时忽略角部,小面取端部4个点求平均值,大面取端部10个点求平均值。可以看出:在实际测试情况中,大面部分进电面和出电面均是中部槽帮最薄,往角部处逐渐变厚,而端部槽帮最厚,这一槽帮厚度变化趋势与计算值是吻合的。此外,测试值与计算结果的平均值误差在3 cm以内,考虑到模型简化带来的误差以及实际生产过程中操作工艺的影响,计算值和测试值在精度上基本吻合。从而验证了算法的有效性。
表2 槽帮厚度计算值与测试值比较
Table 2 Freeze thickness comparison of calculated and tested values
4 结论
(1) 应用APDL语言设计了一种新型的三维槽帮形状计算算法,以300 kA铝电解槽为算例,建立其电热耦合计算模型,通过反复调用ANSYS中的前处理、求解和后处理模块,通过多次循环迭代计算,最终得到收敛的三维槽帮形状。
(2) 与传统2D槽帮的计算相比,3D槽帮算法在准确性等方面体现了诸多优点:首先,3D槽帮形状计算所采用的电热模型将小面和角部等参数包含在内,因此与铝电解槽的实际情况更加相符;其次,模型体现了电流对槽帮的影响,弥补了2D模型计算仅仅考虑热场的不足;最后,计算结果除了大面处槽帮形状外,还很好地得出了小面以及角部的槽帮形状,以及其沿着大小面的变化趋势。通过与实测结果的对比也验证了模型准确性。此外,计算结果也揭示了算例铝电解槽的槽帮厚度由大到小顺序为:角部,小面,大面。这也是与其设计理念是相符的。
(3) 3D槽帮算法可在新型铝电解槽设计时,对槽帮形状进行较为精确的预测,进而为铝电解槽的保温结构等的设计与优化提供技术支撑。
参考文献:
[1] 邓发权. 预焙铝电解槽早期槽帮的建立和后期的维护[J]. 上海有色金属, 2007, 28(1): 26-30.
DENG Fa-quan. Forming and maintenance of pre-bake cell skulls for aluminum electrolysis[J]. Shanghai Nonferrous Metals, 2007, 28(1): 26-30.
[2] Haupin W E. Calculating thickness of containing walls frozen from melt[C]//Edgeworth T C. Light Metals 1971. New York, NY: The Metallurgical Society of AIME, 1971: 188-194.
[3] Pfundt H, Vogelsang D, Gerling U, et al. Calculation of the crust profile in aluminium reduction cells by thermal computer modelling[C]//Campbell P G. Light Metals 1989. Las Vegas, NV: Metallurgical Society of AIME, 1989: 371-377.
[4] Dupuis M. Computation of aluminum reduction cell energy balance using ANSYS finite element models[C]//Welch B J. Light Metals 1998. San Antonio, TX: TMS (The Minerals, Metals & Materials Society), 1998: 409-417.
[5] Bruggeman J N, Danka D J. Two-dimensional thermal modeling of the Hall-Héroult cell[C]//Blckert C M. Anaheim, CA: TMS (The Minerals, Metals & Materials Society), 1990: 203-209.
[6] Kiss L I, Dassylva-Raymond V. Freeze thickness in the aluminium electrolysis cells[C]//Deyoung D H. Light Metals 2008. New Orleans, LA, US: TMS, 2008:431-436.
[7] LI Jie, WANG Zhi-gang, LAI Yan-qing, et al. Cell profile and heat balance of 5 kA inert anode aluminum reduction cells[J]. The Chinese Journal of Process Engineering, 2008(8): 54-58.
[8] LI Xiang-peng, LI Jie, XUE Tie-peng. Simulation calculation of tank hearth profile in large scale prebaked aluminum electrolytic cell[J]. Metallurgical Industry Automation, 2003(4): 30-33.
[9] Dupuis M, Tabsh I. Thermo-electric coupled field analysis of aluminum reduction cells using the ANSYS parametric design language[J]. Pennsylvania: Pittsburgh, 1991(3): 20-24.
[10] 李贺松, 梅炽. 铝电解槽热电场的有限元分析[J]. 中国有色金属学报, 2004, 14(5): 854-859.
LI He-song, MEI Chi. Finite element analysis of thermo-electric coupled field in aluminum reduction cell[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(5): 854-859.
[11] Michel C J. Evolution of the cathodic ohmic drop during the electrolysis in the aluminium cell[C]//Bohner H O. Light Metals 1985. New York, NY, USA: The Metallurgical Society of AIME, 1985: 989-1003.
[12] Sorlie M, Gran H. Cathode collector bar-to-carbon contact resistance[C]//Cutshall E R. Light Metals 1992. San Diego, CA, USA: TMS, 1992: 779-787.
[13] 李景江, 邱竹贤. 铝电解槽槽帮结壳形状的计算机模拟[J]. 东北工学院学报, 1989, 10(3): 232-237.
LI Jing-jiang, QIU Zhu-xian. Computer simulation of the shape of ledge in aluminium electrolysis cell[J]. Journal of Northeast University of Technology, 1989, 10(3): 232-237.
[14] Whitfield D, Skyllas-Kazacos M, Welch B. Metal pad temperatures in aluminium reduction cells[C]//Tabereaux A T. Light Metals 2004. Charlotte: TMS, 2004: 239-243.
[15] 冯乃祥. 铝电解[M]. 北京: 化学工业出版社, 2008: 93-95.
FENG Nai-xiang. Aluminium electrolysis[M]. Beijing: Chemical Industry Press, 2008: 93-95.
(编辑 陈爱华)
收稿日期:2011-05-02;修回日期:2011-07-07
基金项目:教育部高等学校博士学科点专项科研基金资助项目(2010016212008);国家自然科学基金资助项目(51104187)
通信作者:张红亮(1979-),男,湖南岳阳人,博士,副教授,从事冶金过程数值仿真及优化研究;电话:0731-88876454;E-mail: net_hotang@163.com