考虑初始孔隙比影响的水-土特征曲线计算模型

张文振¹，李海潮²，雷华阳¹，刘汉磊³

(1. 天津大学 土木工程系，天津，300072；

2. 中南大学 土木工程学院，湖南 长沙，410083；

3. 中国民航大学 机场学院，天津，300300)

摘要：在FREDLUND & XING模型基础上提出一种水-土特征曲线计算模型，以统一描述初始孔隙比和基质吸力对土的有效饱和度的影响。本文所提模型有较好的连续性和收敛性，适用于不同类型土体的水力特征的描述，其包含的材料参数可以采用最小二乘法由试验结果进行标定。研究结果表明：本模型能够准确地描述非饱和土的水-土特征曲线，并且可反映初始孔隙比的影响。在相同的基质吸力条件下，土的有效饱和度会随初始孔隙比增大而减小，其变化速率则会随基质吸力增大而减小。

关键词：初始孔隙比；水-土特征曲线；数学模型

中图分类号：TU411.4                    文献标志码：A

文章编号：1672-7207（2021）07-2394-08

A soil-water characteristic curve model for soils with considering effect of initial void ratio

ZHANG　Wenzhen¹, LI　Haichao², LEI　Huayang¹, LIU　Hanlei³

(1. Department of Civil Engineering, Tianjin University, Tianjin 300072, China;

2. School of Civil Engineering, Central South University, Changsha 410083, China;

3. School of Airport Engineering, Civil Aviation University of China, Tianjin 300300, China)

Abstract: In order to describe the effects of initial porosity ratio and matric suction on soil effective saturation, a water-soil characteristic curve calculation model was proposed based on FREDLUND & XING model. The proposed model had good continuity and convergence, and it was suitable for the description of hydraulic characteristics of different types of soils. The material parameters contained in the model could be calibrated by the least square method from the test results. The results show that this model can accurately describe the water-soil characteristic curve of unsaturated soil and reflect the influence of initial porosity ratio. For the same matric suction, the effective saturation of soil decreases with the increase of the initial porosity ratio, while the change rate decreases with the increase of matric suction.

Key words: initial void ratio; soil-water characteristic curve; mathematical approach

土的持水特性与土的类型、基质吸力、孔隙结构等因素有关，通常可以采用水-土特征曲线(soil-water characteristic curve，SWCC)进行描述^[1-5]。水-土特征曲线对于分析非饱和土强度和变形等特性具有十分重要的意义^[6-7]。FREDLUND等^[8]指出土中的吸力由基质吸力和渗透吸力2部分组成，其中基质吸力与水的表面张力引起的毛细现象有关，而渗透吸力则与孔隙水的盐浓度有关。在测试水-土特征曲线时，通常不考虑渗透吸力的影响，可以将土的体积含水率θ或有效饱和度S_r表示为基质吸力s的函数，如VAN GENUCHTEN模型^[9]和FREDLUND & XING模型^[10-11]。ARYA等^[12-15]进一步指出土的颗粒粒径分布和孔隙结构会对水-土特征曲线产生影响，且可采用毛细作用理论建立新的计算模型。ANTINORO等^[16]基于ARYA & PARIS模型提出了一个确定砂土水-土特征曲线的简单方法；徐晓兵等^[17]提出了ARYA & PARIS模型的微分形式来描述级配曲线演化对可降解土的持水特性的影响。此外，徐永福等^[18]基于分形理论建立了新的水-土特征曲线模型。陶高梁等^[19-20]结合孔隙分布变化规律阐述了非饱和土在压缩变形条件下的水-土特征曲线的演化机理，并且提出了简化表征方法。

尽管上述模型在工程实践中得到了广泛的应用，但这些模型在描述不同初始孔隙比条件非饱和土的水-土特征曲线时存在一定的不足。如在相同基质吸力条件下土有效饱和度S_r会随初始孔隙比e₀增大而逐渐减小^[21-22]，该现象可能与土的双孔隙结构和变形有关^{[7, 23]}。在此基础上，ZHOU等^[24]建立了考虑初始孔隙比影响的水-土特征曲线增量表达式，该计算模型与GALLIPOLI等^[25]提出的修正VAN GENUCHTEN模型在形式上较接近。陶高梁等^[26]及张昭等^[27]则分别基于分形理论和“水土体积比”的概念对该现象进行了解释。

本文作者提出了一种水-土特征曲线模型来统一描述基质吸力和初始孔隙比对非饱和土的持水能力的影响。该模型形式较为简单，其包含的材料参数可以采用最小二乘法由试验结果进行标定。通过将模型计算结果与不同类型土的试验结果进行对比分析，以验证本文模型描述非饱和土的水-土特征曲线的准确性，并且考虑初始孔隙比的影响。

1  数学模型

1.1　水-土特征曲线

通常可采用轴平移技术测量非饱和土的基质吸力，得到其水-土特征曲线，主要可以分为饱和区、过渡区和残留区3部分，如图1所示。由图1可知：当基质吸力s为0 MPa时，土体处于饱和状态，其有效饱和度S_r为1.0。当基质吸力大于进气值(饱和土脱水过程中开始进入空气时的吸力)时，随s逐渐增大，S_r会逐渐减小并最终达到其残余值。

图1　水-土特征曲线示意图

Fig. 1　Schematic diagram of soil-water characteristic curve

为了考虑残余有效饱和度的影响，ZHOU等^[24]建议将非饱和土的水-土特征曲线表示为

(1)

式中：和分别为参考有效饱和度和残余有效饱和度。

当采用VAN GENUCHTEN模型来描述非饱和土的水-土特征曲线时，可以表示为

(2)

式中：α，n和m均为材料参数。

根据式(1)和式(2)，当基质吸力s等于0 MPa时，有且；而当s趋近于无穷大时，将近似于0，此时土将达到其残余有效饱和度。

初始孔隙比e₀会对非饱和土的水-土特征曲线产生影响，因此，GALLIPOLI等^[25]建议将VAN GENUCHTEN模型改写为

(3)

式中：e为孔隙比；φ和ψ为额外引入的材料参数。

对式(3)进行求导，可以得到关于e的导数为

(4)

式(4)与ZHOU等^[24]提出的水-土特征曲线的增量表达式在形式上较类似，两者均能够合理地描述初始孔隙比对水-土特征曲线的影响。

1.2　本文模型

本文基于FREDLUND & XING模型，提出一种考虑初始孔隙比影响的水-土特征曲线计算模型。相比VAN GENUCHTEN模型，FREDLUND & XING模型对于水-土特征曲线的高吸力区域有着更好的连续性和收敛性。根据FREDLUND等^[10]描述，水-土特征曲线可表示为

(5)

式中：s_r为材料参数。

参考GALLIPOLI等^[25]，本文对式(5)进行了适当简化，从而得到如下考虑初始孔隙比影响的的表达式，

(6)

式中：e_r为参考初始孔隙比。

将式(6)代入式(1)中，可以将非饱和土的有效饱和度S_r最终表示为

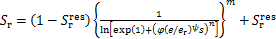(7)

式(7)可统一描述基质吸力s和孔隙比e对非饱和土的水-土特征曲线的影响。在描述不同初始孔隙比条件下土的水-土特征曲线时，可先采用某特定初始孔隙比e_i0所对应的试验结果为参考状态，通过最小二乘法确定材料参数φ，n和m。然后采用选取合适的ψ来描述不同初始孔隙比对应的水-土特征曲线，此时参考孔隙比e_r等于e_i0。

1.3　模型对比

为了验证本文提出的考虑初始孔隙比影响的水-土特征曲线数学模型的适用性，采用Boom黏土^[28]的试验结果进行模拟，其初始孔隙比e₀分别为0.59和0.93。GALLIPOLI模型和本文模型的计算结果如图2所示，表1所示为两者所包含的材料参数的取值。

图2　初始孔隙比对水-土特征曲线的影响及模型计算结果对比^[28]

Fig. 2　Effect of initial void ratios on soil-water characteristic curves and model calculation compasion^[28]

表1　CALLIPOLI模型和本文模型材料参数

Table 1　Model parameters of CALLIPOLI model and proposed model

由图2可知：本文模型能够准确地描述不同初始孔隙比条件下Boom黏土的水-土特征曲线，并且在相同基质吸力条件下，试样的有效饱和度会随初始孔隙比增大而逐渐减小。此外，本文模型与GALLIPOLI模型计算结果较接近，在低基质吸力条件下两者的结果几乎保持一致，不过随基质吸力逐渐增大，模型计算得到的有效饱和度要略微偏大。

在此基础上，得到三维条件下初始孔隙比和基质吸力对非饱和土的有效饱和度的影响，如图3所示，其中材料参数取值与表1保持一致。由图3可知：在相同的基质吸力条件下，试样的有效饱和度会随初始孔隙比增大而逐渐减小。

图3　有效饱和度S_r随初始孔隙比e₀和基质吸力s的变化

Fig. 3　Vovriations of effective saturation S_r against with initial void ratio e₀ and suction s

1.4　参数敏感性分析

本节探究材料参数φ，n和m对模型计算结果的影响，假定试样的初始孔隙比e₀和参考初始孔隙比e_r分别为0.93和0.59，其余材料参数见表1。

材料参数φ，n和m对试样的水-土特征曲线的影响如图4所示。由图4可以看出：保持基质吸力不变，增大φ会导致试样的有效饱和度逐渐减小，该影响会随基质吸力增大而逐渐减小；当基质吸力s=1 MPa时，不同n对应的水-土特征曲线将交于一点。而当基质吸力小于该特征值时，增大n会导致试样的有效饱和度逐渐增大，反之则逐渐减小；增大m会导致试样的水-土特征曲线具有向下移动的趋势，此时需要施加更大的基质吸力才会使试样的有效饱和度趋近于其残余值。

图4　材料参数对水-土特征曲线的影响

Fig. 4　Effect of material parameters on water-soil characteristic curves

上述计算结果初步表明，本文提出的水-土特征曲线模型能够合理地描述初始孔隙比和基质吸力对非饱和土的持水特性的影响。

2  模型验证

为了进一步验证模型对于不同类型土的水-土特征曲线的计算效果，分别采用击实土^[29]、粉砂^[30]、Barcelona重塑土^[31]和黏质砂土^[32]的试验结果。表2所示为不同类型土的材料参数。

表2　不同类型土的材料参数

Table 2　Model parameters of different kinds of soil

2.1　击实土

VANAPALLI等^[29]采用击实方法得到初始孔隙比分别为0.517，0.474和0.444的重塑土试样，并且测得了其水-土特征曲线。试验结果和模型计算结果如图5所示，在计算过程中可以采用e₀=0.517对应的试样的试验结果对本文模型的材料参数进行标定。由图5可知：不同初始孔隙比所对应的试样的水-土特征曲线具有明显的差异，而本文模型能够对此进行准确的描述。

图5　不同初始孔隙比条件下击实土^[29]水-土特征曲线和模型计算结果

Fig. 5　Water-soil characteristic curves and model calculation results of compacted soil^[29] under different initial porosity ratios

2.2　粉砂

HUANG等^[30]通过室内试验探究了不饱和粉砂的水力特性，该砂土包含52.5%的砂土、37.5%的粉土和10%的黏土，其重度、液限和塑限分别为2.68%，22.2%和16.6%。

不同初始孔隙比所对应的试样的试验结果和模拟结果如图6所示。从图6可以看出：尽管初始孔隙比会对粉砂的水-土特征曲线产生影响，但由于试样的持水能力较弱，作用并不明显，尤其是当基质吸力接近250 kPa时，不同初始孔隙所对应的试样的有效饱和度S_r几乎相同，约等于0.3。由模拟结果可得本文模型同样适用于粉砂的水-土特征曲线的数学描述。

图6　不同初始孔隙比条件下粉砂^[30]水-土特征曲线和模型计算结果

Fig. 6　Water-soil characteristic curves and model calculation results of silt^[30] under different initial porosity ratios

2.3　Barcelona重塑土

TARANTINO等^[31]通过试验探究了初始孔隙比对Barcelona重塑土的水-土特征曲线的影响。试样过程中，对泥浆分别施加100，300和500 kPa的固结压力，从而得到初始孔隙比e₀分别为0.62，0.54和0.50的试样。

Barcelona重塑土的水-土特征曲线试验结果和模型计算结果如图7所示。由图7可知：本文模型能够较准确地反映不同初始孔隙比对试样的持水能力的影响，不过当e₀分别为0.54和0.50时，在高基质吸力区域本文模型计算得到的有效饱和度比试验结果大。

图7　不同初始孔隙比条件下Barcelona重塑土^[31]水-土特征曲线和模型计算结果

Fig. 7　Water-soil characteristic curves and model calculation results of Barcelona remoulded clay^[31] under different initial porosity ratios

2.4　黏质砂土

本模型模拟了黏质砂土的水-土特征曲线试验结果，如图8所示。根据SALAGER等^[32]研究可知，该黏质砂土由72%的砂土、18%的粉土和10%的黏土组成。

图8　不同初始孔隙比条件下黏质砂土^[32]水-土特征曲线和模型计算结果

Fig. 8　Water-soil characteristic curves and model calculation results of clayey sand^[32] under different initial porosity ratios

由图8可知：当试样的初始孔隙比e₀由1.01减小至0.55时，试样的持水能力会逐渐增强；该试验结果同样表明，初始孔隙比对土的持水能力的影响程度会随基质吸力增大而逐渐减弱。尽管本文模型能够大体上反映该变化规律，不过其拟合效果有待进一步提升。

3  结论

1) 在相同基质吸力条件下，增大初始孔隙比会逐渐减小土的有效饱和度，其变化速率会随基质吸力增大而减小。

2) 对FREDLUND & XING水-土特征曲线计算模型进行适当的简化，并且考虑了初始孔隙比的影响。该模型所包含的材料参数的具体取值可以采用最小二乘法由试验结果拟合得到。

3) 该模型能够准确地描述不同类型土的水-土特征曲线试验结果，在岩土工程领域中有着广泛的应用前景。

4) 初始孔隙比之所以会对土的持水能力产生影响可能与其微观结构的改变有关，而本文模型无法揭示其作用机理，可以在后续的研究中对其进行进一步拓展，进而从微观的角度更深刻地认识土的水力特性。

参考文献：

[1] TULLER M, OR D. Retention of water in soil and the soil water characteristic curve[J]. Encyclopedia of Soils in the Environment, 2004, 4: 278-289.

[2] FREDLUND M D, WILSON G W, FREDLUND D G. Use of the grain-size distribution for estimation of the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 2002, 39(5): 1103-1117.

[3] REN Xingwei, KANG Jianyu, REN Junjie, et al. A method for estimating soil water characteristic curve with limited experimental data[J]. Geoderma, 2020, 360(15): 114013.

[4] ZHAI Qian, RAHARDJO H, SATYANAGA A, et al. Estimation of the soil-water characteristic curve from the grain size distribution of coarse-grained soils[J]. Engineering Geology, 2020, 267(20): 105502.

[5] 杨松, 吴珺华. 粉土表面液滴蒸发特性及对土-水特征曲线的影响[J]. 岩土力学, 2020, 41(S2): 1-9.

YANG Song, WU Junhua. Evaporation characteristics of liquid drops on silt soil surface and the influences on soil-water characteristic curve[J]. Rock and Soil Mechanics, 2020, 41(S2): 1-9.

[6] 褚峰, 邵生俊, 陈存礼. 干密度和竖向应力对原状非饱和黄土土水特征影响的试验研究[J]. 岩石力学与工程学报, 2014, 33(2): 413-420.

CHU Feng, SHAO Shengjun, CHEN Cunli. Experimental research on influences of dry density and vertical stress on soil-water characteristic curves of intact unsaturated loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 413-420.

[7] 李锦辉, 郭凌波, 张利民. 考虑裂隙动态变化时裂隙土土水特征曲线的预测方法研究[J]. 岩石力学与工程学报, 2013, 32(6): 1288-1296.

LI Jinhui, GUO Lingbo, ZHANG Limin. Prediction of SWCC for unsaturated cracked soil considering development process of cracks[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1288-1296.

[8] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils[M]. Hoboken: John Wiley & Sons, Inc., 1993: 42-45.

[9] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898.

[10] FREDLUND D G, XING Anqing. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532.

[11] FREDLUND D G, XING Anqing, HUANG Shangyan. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 533-546.

[12] ARYA L M, PARIS J F. A physicoempirical model to predict the soil moisture characteristic from particle-size distribution and bulk density data[J]. Soil Science Society of America Journal, 1981, 45(6): 1023-1030.

[13] 张升, 颜瀚, 滕继东, 等. 一个冻土的渗透系数模型及其验证[J]. 岩土工程学报, 2020, 42(11): 2146-2152.

ZHANG Sheng, YAN Han, TENG Jidong, et al. New model for hydraulic conductivity of frozen soils[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(11): 2146-2152.

[14] ZHAI Qian, RAHARDJO H, SATYANAGA A, et al. Estimation of the soil-water characteristic curve from the grain size distribution of coarse-grained soils[J]. Engineering Geology, 2020, 267: 105502.

[15] PASHA A, KHOSHGHALB A, KHALILI N. Evolution of isochoric water retention curve with void ratio[J]. Computers and Geotechnics, 2020, 122: 103536.

[16] ANTINORO C, BAGARELLO V, FERRO V, et al. A simplified approach to estimate water retention for Sicilian soils by the Arya-Paris model[J]. Geoderma, 2014, 213: 226-234.

[17] 徐晓兵, 陈云敏, 张旭俊, 等. 基于颗分曲线预测可降解土体土水特征曲线的初探研究[J]. 土木工程学报, 2016, 49(12): 108-113.

XU Xiaobing, CHEN Yunmin, ZHANG Xujun, et al. Prediction on the soil-water characteristic curve of degradable soil from particle-size distribution curve[J]. China Civil Engineering Journal, 2016, 49(12): 108-113.

[18] 徐永福, 黄寅春. 分形理论在研究非饱和土力学性质中的应用[J]. 岩土工程学报, 2006, 28(5): 635-638.

XU Yongfu, HUANG Yinchun. Fractal-textured soils and their unsaturated mechanical properties[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 635-638.

[19] 陶高梁, 张季如, 庄心善, 等. 压缩变形影响下的土-水特征曲线及其简化表征方法[J]. 水利学报, 2014, 45(10): 1239-1246.

TAO Gaoliang, ZHANG Jiru, ZHUANG Xinshan, et al. Influence of compression deformation on the soil-water characteristic curve and its simplified representation method[J]. Journal of Hydraulic Engineering, 2014, 45(10): 1239-1246.

[20] 陶高梁, 孔令伟, 肖衡林, 等. 土-水特征曲线的分形特性及其分析拟合[J]. 岩土力学, 2014, 35(9): 2443-2447.

TAO Gaoliang, KONG Lingwei, XIAO Henglin, et al. Fractal characteristics and fitting analysis of soil-water characteristic curves[J]. Rock and Soil Mechanics, 2014, 35(9): 2443-2447.

[21] JOTISANKASA A, RIDLEY A, COOP M. Collapse behavior of compacted silty clay in suction-monitored oedometer apparatus[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 867-877.

[22] ZHAI Qian, RAHARDJO H, SATYANAGA A, et al. Framework to estimate the soil-water characteristic curve for soils with different void ratios[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(8): 4399-4409.

[23] XIE Xiao, LI Ping, HOU Xiaokun, et al. Microstructure of compacted loess and its influence on the soil-water characteristic curve[J]. Advances in Materials Science and Engineering, 2020: 3402607.

[24] ZHOU A N, SHENG D, CARTER J P. Modelling the effect of initial density on soil-water characteristic curves[J]. Géotechnique, 2012, 62(8): 669-680.

[25] GALLIPOLI D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio[J]. Géotechnique, 2012, 62(7): 605-616.

[26] 陶高梁, 孔令伟. 不同初始孔隙比土体进气值及土-水特征曲线预测[J]. 岩土工程学报, 2018, 40(S1): 34-38.

TAO Gaoliang, KONG Lingwei. Prediction of air-entry value and soil-water characteristic curve of soils with different initial void ratios[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S1): 34-38.

[27] 张昭, 刘奉银, 赵旭光, 等. 考虑应力引起孔隙比变化的土水特征曲线模型[J]. 水利学报, 2013, 44(5): 578-585.

ZHANG Zhao, LIU Fengyin, ZHAO Xuguang, et al. A soil water characteristic curve model considering void ratio variation with stress[J]. Journal of Hydraulic Engineering, 2013, 44(5): 578-585.

[28] ROMERO E, GENS A, LLORET A. Water permeability, water retention and microstructure of unsaturated compacted boom clay[J]. Engineering Geology, 1999, 54(1/2): 117-127.

[29] VANAPALLI S K, FREDLUND D G, PUFAHL D E. The influence of soil structure and stress history on the soil-water characteristics of a compacted till[J]. Géotechnique, 1999, 49(2): 143-159.

[30] HUANG Shangyan, BARBOUR S L, FREDLUND D G. Development and verification of a coefficient of permeability function for a deformable unsaturated soil[J]. Canadian Geotechnical Journal, 1998, 35(3): 411-425.

[31] TARANTINO A. A water retention model for deformable soils[J]. Géotechnique, 2009, 59(9): 751-762.

[32] SALAGER S, EL YOUSSOUFI M S, SAIX C. Definition and experimental determination of a soil-water retention surface[J]. Canadian Geotechnical Journal, 2010, 47(6): 609-622.

(编辑  刘锦伟)

收稿日期： 2021 -01 -07； 修回日期： 2021 -03 -05

基金项目(Foundation item)：国家重点研发计划项目(2017YFC0805402)；土木工程防灾国家重点实验室开放基金项目(SLDRCE17-01)；国家自然科学基金(52078334) (Project(2017YFC0805402) supported by the National Key Research and Development Program of China; Project(SLDRCE17-01) supported by the Open Fund Project of the State Key Laboratory of Civil Engineering Disaster Prevention; Project(52078334) supported by the National Natural Science Foundation of China)

通信作者：雷华阳，博士，教授，从事岩土工程领域研究；E-mail：leihuayang74@163.com

DOI: 10.11817/j.issn.1672-7207.2021.07.025

引用格式： 张文振, 李海潮, 雷华阳, 等. 考虑初始孔隙比影响的水-土特征曲线计算模型[J]. 中南大学学报(自然科学版), 2021, 52(7): 2394-2401.

Citation: ZHANG Wenzhen, LI Haichao, LEI Huayang, et al. A soil-water characteristic curve model for soils with considering effect of initial void ratio[J]. Journal of Central South University(Science and Technology), 2021, 52(7): 2394-2401.