J. Cent. South Univ. Technol. (2010) 17: 1139-1143

DOI: 10.1007/s11771-010-0609-y

Influence of Ti4+ doping on hyperfine field parameters of Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0≤x≤0.7)

KUMAR S¹, PRAKASH R², ALIMUDDIN³, CHOI H K¹, KOO B H¹, SONG J I²,

CHUNG H⁴, JEONG H⁴, LEE C G¹

1. School of Nano and Advanced Materials Engineering, Changwon National University,

Changwon 641-773, Korea;

2. Department of Mechanical Engineering, Changwon National University, Changwon 641-773, Korea;

3. Department of Applied Physics, Aligarh Muslim University, Aligarh 202002, India;

4. Department of Precision & Mechanical Engineering and BK21 Eco-Friendly Heat & Cooling Energy Mechanical Research Team, Gyeongsang National University, Tongyeong 650-160, Korea

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: The mixed spinel ferrite system Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0≤x≤0.7) was synthesized by the conventional solid-state reaction technique. The effect of Ti⁴⁺ doping was studied by using the M?ssbauer spectroscopy measurements at room temperature. From the analysis of the M?ssbauer spectra, it is observed that s-electron density, electric field gradient (EFG), quadrupole coupling constant (QCC) and the net hyperfine magnetic fields acting on the M?ssbauer nuclei–Fe_A³⁺ and Fe_B³⁺ change with the increase of Ti⁴⁺ doping in Mg_0.95Mn_0.05Fe₂O₄. The hyperfine magnetic field decreases with the increase of Ti⁴⁺ doping.

Key words: spinel ferrite; M?ssbauer spectroscopy; hyperfine magnetic field; isomer shift; Ti⁴⁺ doping

1 Introduction

Transition metal ferrites are a family of oxides having great technological importance because of their novel physical properties. These ferrite materials can be used in the fabrication of the magnetic, electronic and microwave devices such as thermostats and recording media. The basis for the wide range of applications is related to the variety of transition metal cations that can be incorporated into the lattice of the parent magnetic structure. Since the spin structure in spinel ferrites is intricately attached to the cation occupancy of interstitial sites having either tetrahedral or octahedral symmetry within a close-packed oxygen lattice. The magnetic properties of spinel ferrites, such as transition temperature and saturation magnetic moment, strongly depend on the distribution of cations; and such magnetic properties have been studied widely for several decades [1-2]. In general, the cation distribution in these materials have the form: (A_1-xM_x)[A_xM_2-x]O₄, where A and M are divalent and trivalent ions, respectively, and x is called the inversion parameter. The round and square brackets denote the cations located at the center of the tetrahedral (A) lattice of oxygen and those at the octahedral (B) lattice, respectively. The superexchange interaction between the spins at sites A and B (A-B interaction, J_AB) is stronger than that among the spins at site A (A-A interaction, J_AA) or site B (B-B interaction, J_BB), because the wave function overlaps of the cations and oxygen ions are different. This is the main cause due to the fact that the magnetic property of spinel ferrite strongly depends on the degree of inversion [3]. In spinel ferrites, ferrimagnetic ordering occurs because the negative exchange interaction J_AB between magnetic cations occupying sites A and B dominates the negative intra sublattice exchange interactions J_AA and J_BB, causing each of the two magnetic sublattices on sites A and B to be aligned and frustrated. Early experiments showed that significant replacements of magnetic cations were seen to cause a reduction in sample magnetization, which was described as a spin canting mechanism by YAFET and KITTEL [4]. Furthermore, the dilution of magnetic ions provides a wonderful richness of magnetic behaviors, including antiferromagnetic, spin-glass, canted ferrimagnet, or more complex magnetic orderings, and results to construct magnetic phase diagrams as a function of magnetic cation occupancy of sites A and B[5-6].

Magnesium-manganese (Mg-Mn) ferrites are attractive materials for high frequency applications because of their high resistivity (＞10⁸ Ω?cm) and low eddy current loss. These ferrites are also extensively useful as storage elements and memory devices in computers and other devices because of low coercive field. Thus, in this work the influence of diamagnetic Ti⁺⁴ ions in Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0≤x≤0.7) was studied using M?ssbauer spectroscopy.

2 Experimental

The specimens of mixed spinel ferrite Mg_0.95Mn_0.05- Fe_2-2xTi_2xO₄ (0≤x≤0.7) were prepared by using a conventional solid-state reaction method. The starting materials were Mg(NO₃)₂, FeO, TiO₂ and MnO₂.  The stoichiometric amounts of highly pure powder were mixed thoroughly and pre-calcinated at 1 000 ℃ for  12 h. The pre-calcinated materials were again ground and calcinated at 1 250 ℃ for 24 h. Finally, the samples were ground to fine powders, pressed into pellet form, and sintered at 1 300 ℃ for 24 h, and at the end of each heat treatment the samples were allowed to cool slowly to room temperature. Powder X-ray diffraction (XRD) was performed using Bruker AXE D8 X-ray powder diffractometer with Cu K_α radiation at room temperature. M?ssbauer spectra of the samples were recorded using a conventional constant acceleration spectrometer in transmission geometry with a ⁵⁷Co source in Rh matrix at room temperature in the absence of magnetic field. The experimentally observed spectra were fitted using a NORMOS (SITE/DIST) program [7]. All spectra were calibrated with respect to α-Fe. The s-electron density (ΔS) is calculated using the formula

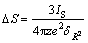                              (1)

where I_S is the isomer shift; z is atomic number; e is charge of electron; and  is mean square radius of the M?ssbauer nucleus.

3 Results and discussion

The M?ssbauer spectra of Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0≤x≤0.7) were recorded at room temperature in the absence of magnetic field. The spectra have two sextets: one is attributed to Fe⁺³ at site A and the other is attributed to Fe⁺³ at site B. Both the sextets are due to magnetic hyperfine interactions of the Zeeman pattern. The two sextets remain present up to x= 0.5 but have diminishing trend in their peaks, and from x=0.2 to x= 0.6, one doublet starts to appear and becomes maximum when x=0.6 (see Figs.1-3). In Figs.1-3 the change in isomer shift (I_S) is insignificant with increasing concentration of Ti⁴⁺. This implies that the addition of Ti⁴⁺ does not affect the s-electron density of Fe³⁺ in the Mg-Mn ferrites. It is known that isomer shift for site B is more than that for site A. In cubic spinel ferrites the bond separation Fe³⁺-O^2- is larger for site B as compared to that for site A because the overlapping of orbits of Fe³⁺ ions is smaller at site B and thus a larger isomer shift takes place and more s-electron density at site B emerges [8-9]. However, the observed values of isomer shift at sites A and B, within experimental error, are comparable, which may indicate that the valence effects of Fe³⁺ ions at both the sites are similar with increasing the concentration of Ti⁴⁺. The range of values of s-electron densities implies that iron exists in Fe⁺³ valence state with high spin configuration in the prepared samples [10].

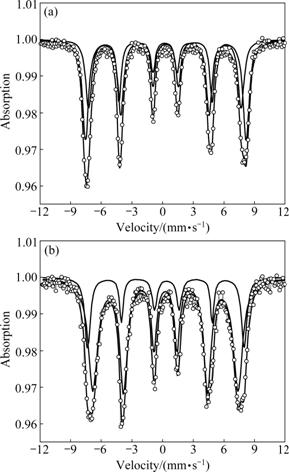
Fig.1  M?ssbauer spectra of Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0≤x≤0.1) system recorded at room temperature: (a) x=0; (b) x=0.1

Tables 1 and 2 list the hyperfine parameters calculated for Ti⁴⁺ doped Mg-Mn ferrites samples. It is observed that some of QCC values are negative and some are positive, which may be due to the fact that when transition takes places from higher energy level (m=±1/2 state) to lower energy level (m=±3/2 state), and QCC leads to negative values, otherwise positive values. Simple calculation verifies this fact. The quadrupole splitting (Q_S) for all the spectra up to x=0.5 is found to be negligibly small, which means small QCC and hence weak quadrupole interaction. It is attributed to the fact that the symmetry between Fe³⁺ ions and their surrounding is very close to cubic symmetry. However, comparison of QCC reveals that the QCC due to site B is more than that due to site A because site B is more distorted than site A and the distortion at the tetrahedral site is caused by the influence of the electric field generated at site B. The magnetic field B_HF (hyperfine magnetic field) due to ions own electrons remains constant because d⁵ electrons do not change while the magnetic ions are diluted systematically by non-magnetic ions (Ti⁴⁺). As a consequence, B_HF due to lattice has decreasing trend.

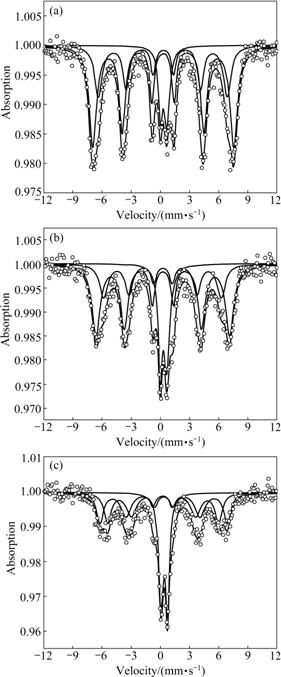
Fig.2  M?ssbauer spectra of Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0.2≤x≤0.4) system recorded at room temperature: (a) x=0.2; (b) x= 0.3; (c) x=0.4

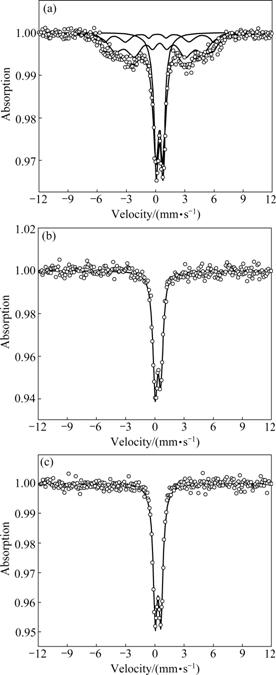
Fig.3 M?ssbauer spectra of Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ (0.5≤x≤0.7) system recorded at room temperature: (a) x=0.5; (b) x=0.6; (c) x=0.7

Fig.4 shows the variation of the hyperfine magnetic field at sites A and B vs Ti⁴⁺ concentration in Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ ferrites. In most of the ferrites, B-site hyperfine field is larger than that of A-site, which is attributed to the dipolar field due to deviation from the cubic symmetry and covalent nature of the tetrahedral bonds [7, 9]. The observed variation in hyperfine magnetic fields at sites A and B with increasing concentration of Ti in Mg-Mn ferrites can be qualitatively explained using Neel’s superexchange interactions [11]. According to Neel’s model, intersublattice interactions, i.e., AB exchange interactions are stronger than intra-sublattice exchange interactions, i.e., AA or BB exchange interactions. The experimental observations show that B_HFA＜B_HFB but not B_HFA<HFB (Table 1). This suggests that the spin orientation of the Fe³⁺ (5μ_B) (where μ_B denotes Bohr magnetron) and Mn²⁺ (5μ_B) must have minimum energy configuration. Thus, possible interactions are: Fe³⁺_A-O-Fe³⁺_B, Fe^3+­_A-O-Mn²⁺_B, Fe³⁺_A-O-Mg²⁺_B and Fe³⁺_A-O-Ti⁴⁺_B. The first two are very strong whereas the last two are ineffective because Mg²⁺ and Ti⁴⁺ are non-magnetic. Also, the magnetic field is different and has decreasing trend because of different symmetries of sites A and B and distribution of Fe³⁺ ions, which are replaced by non-magnetic Ti⁴⁺ ions. Thus, the former two AB interactions contribute the maximum and the later two do nothing because AA and BB interactions are much weaker. Consequently, the addition of non-magnetic ion Ti⁴⁺ reduces magnetic ion (Fe³⁺) at both the sublattices, thereby, lowering the net magnetic field as supported by the experimental results. One can also have a look at magnetic fields B_latticeA, B_latticeB at sites A and B separately and find that both fields have the same trend.

Table 1 Calculated values of isomer shift (I_S), s-electron density, quadrupole splitting (Q_S), quadrupole coupling constant (QCC) and electric field gradient (EFG) corresponding to paramagnetic doublet of Mg_0.95Mn_0.05Fe_2-2xTi_2-2xO₄

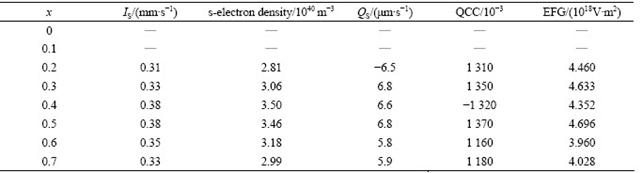
Table 2 Calculated values of isomer shift (I_S), s-electron density, quadrupole splitting (Q_S), quadrupole coupling constant (QCC), electric field gradient (EFG) and hyperfine magnetic field (B_HF) corresponding to Zeeman sextets of Mg_0.95Mn_0.05Fe_2-2xTi_2-2xO₄

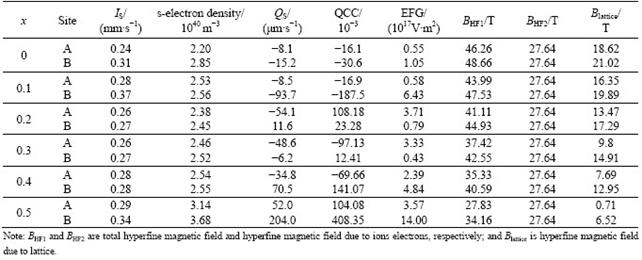
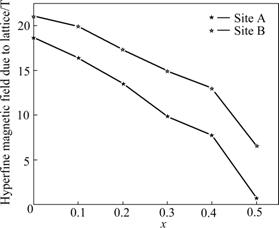
Fig.4 Plot of hyperfine magnetic field as function of Ti⁴⁺ concentration in Mg_0.95Mn_0.05Fe_2-2xTi₂O₄ ferrites

4 Conclusions

(1) The M?ssbauer study performed on Ti doped Mg-Mn ferrites prepared through conventional solid-state reaction method shows change in hyperfine field parameters.

(2) From the above studies a co-existence of the quadrupole as well as the magnetic hyperfine interactions is observed in the system and the calculated value of QCC shows that some values of QCC are negative and some are positive. 

(3) It is also concluded from the analysis of the spectra that the quadrupole interaction increases whereas the magnetic hyperfine interaction decreases.

References

[1] BRABERS V A M. Handbook of magnetic materials [M]. Amsterdam: Elsevier, 1995: 8.

[2] KUMAR S, KUMAR R, DOGRA A, REDDY V R, BANERJEE A, ALIMUDDIN. M?ssbauer and magnetic studies of multiferroic Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ system [J]. Journal of Applied Physics, 2006, 99(8): 08M910.

[3] BURGHART F J, POTZEL W, KALVIUS G M, SCHREIER E, GROSSE G, NOAKES D R, SCHAFER W, KOCKELMANN W, CAMPBELL S J, KACZMAREK W A, MARTIN A, KRAUSE M K. Magnetism of crystalline and nanostructured ZnFe₂O₄ [J]. Physica B: Condensed Matter, 2000, 289/290: 286-290.

[4] YAFET Y, KITTEL C. Antiferromagnetic arrangements in ferrites [J]. Physical Review, 1952, 87(2): 290-294.

[5] DORMANN J M, NOGUES M. Magnetic structures in substituted ferrites [J]. Journal of Physics: Condensed Matter, 1990, 2(5): 1223-1238.

[6] COEY J M D. Noncollinear spin structures [J]. Canadian Journal of Physics, 1987, 65(10): 1210-1232.

[7] BRAND R A, LAUER J, HERLACH D M. The evaluation of hyperfine field distributions in overlapping and asymmetric M?ssbauer spectra: A study of the amorphous alloy Pd_77.5-xCu₆Si_16.5Fe_x [J]. Journal of Physics F: Metal Physics, 1983, 13(3): 675-684.

[8] SCHOENBERG E A. Ferrites for microwave circuits and digital computers [J]. Journal Applied Physics, 1954, 25(2): 152-154.

[9] BABA P D, GYORGY E M, SCHNETTLER F J. Two-phase ferrites for high-speed switching [J]. Journal Applied Physics, 1963, 34(4): 1125-1126.

[10] DICKSON D P E, BERRY F J. M?ssbauer spectroscopy [M]. London: Cambridge University Press, 1986: 22.

[11] NEEL L. Magnetic properties of ferrites: ferrimagnetism and antiferromagnetism [J]. Annual Physics, 1948, 3: 137-198.

(Edited by CHEN Wei-ping)

Corresponding authors: KUMAR S, PhD, Research Professor; Tel: +82-55-2133701; E-mail: shailuphy@gmail.com; LEE C G, PhD, Professor; Tel: +86-55-213370; E-mail: chglee@changwon.ac.kc