面心立方和亚稳液相Cu的电子结构和物理性质
陶辉锦, 谢佑卿, 彭红建,余方新,刘锐锋,李晓波
(中南大学 材料科学与工程学院,湖南 长沙,410083)
摘要:根据SGTE数据库的晶格稳定参数和Debye-Grüneisen模型,运用纯金属单原子(OA) 理论研究了面心立方和亚稳液相Cu的原子状态、原子势能、原子动能、原子体积、体弹性模量和热膨胀系数等物理参数随温度的变化关系。研究结果表明:电子结构计算结果与采用第一原理方法所得的结果一致;单键半径,原子动能和原子势能随温度上升而增加;线热膨胀系数计算值与实验值较吻合;固液相变时,Liquid-Cu的自由电子和共价电子均向非键电子转移,共价d电子向共价s电子转移,电子结构的转变降低液相的导电性,削弱液相原子配位的方向性,引起原子单键半径和体积增大。
关键词:FCC-Cu;Liquid-Cu;电子结构;Debye-Grüneisen模型;CALPHAD方法
中图分类号:TG111 文献标识码:A 文章编号:1672-7207(2007)01-0001-08
Electronic structures and physical properties of FCC
and metastable liquid Cu metals
TAO Hui-jin, XIE You-qing, PENG Hong-jian, YU Fang-xin, LIU Rui-feng, LI Xiao-bo
(School of Materials Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Combining the lattice stability parameters of SGTE database with Debye-Grüneisen model, the atom states, atomic potential and vibrating energies, atomic volumes, bulk moduli and linear thermal expansion coefficients of FCC and metastable Liquid Cu metals in SGTE database of pure elements were studied using one-atom(OA) theory. The results show that calculated electronic structures agree well with those of first principles; the single bond radius, atomic vibrating energy and atomic potential energy increase with the increase of temperature; the linear thermal expansion coefficients agree well with the experimental data as well; and when FCC-Cu is transformed into Liquid-Cu, the free and covalent electrons are transferred into nonbonding electrons, the covalent electrons in d orbital are transferred into s orbital and this change of electronic structures leads to the decrease of electrical conductivity, the weakening of direction of atom bonding, the increase of the single bond radius and the atomic volumes of Liquid-Cu.
Key words: FCC-Cu;Liquid-Cu;electronic structure;Debye-Grüneisen model; CALPHAD method
相图的计算模拟(CALPHAD)是指导新材料开发设计的强有力工具[1-2]。对纯单质不同晶体结构相对Gibbs能即晶格稳定参数的评估是CALPHAD的重要基础,为此,需要对大量二元热力学体系进行实验测量,计算评估和外推来评估这一参数[3]。其中,SGTE(Scientific Group Thermodata Europe) 纯单质数据库[4]给出了298.15 K以上78种元素的不同晶体结构的Gibbs能表达式和相应的晶格稳定参数。第一原理对势函数和波函数进行合理设计,在不依赖实验资料的情况下可以确定纯单质不同晶体结构的相对稳定性。Y.Wang等[5]用第一原理方法系统研究了78种纯单质FCC, HCP 和 BCC结构的相对稳定性,并与采用CALPHAD方法所得的结果进行对比,发现二者存在较大差别[5]。合金系统科学框架(Systematic sciences of alloys, SSA)[6]的建立正是为了减小甚至消除这种差别,探索对纯金属与合金电子结构、热力学性质和物理性质的统一描述。SSA框架以多原子相互作用 势[7-8]、晶格常数方程[9]、原子状态杂化理论[10-11]和其他物理性质的理论作为基础,对Ag-Cu[12-15],Ti-Al[16-18]和Au-Cu[19-21]等合金系的原子状态、原子势能、原子动能、原子体积、体弹性模量和热膨胀系数等参数随温度和成分的变化规律进行研究。在SSA框架中,最基础的工作是对各种不同晶体结构纯单质的状态和性质随温度的变化关系进行计算模拟,单原子(One atom, OA)理论则是这一工作的理论基础。在此,本文作者将CALPHAD方法的晶格稳定参数与Debye-Grüneisen模型相结合,运用OA理论确定新的理论计算线路,并根据这一线路计算面心立方和亚稳液相Cu的电子结构,以及它们的物理性质随温度的变化关系。
1 原理与方法
1.1 纯金属单原子理论
1.1.1 原子状态参数
与稳定的自由原子相比,凝聚态金属中的原子是通过化学键结合的。因此,金属原子外层的电子可以按照功能分为成键和非成键两大类[22]。金属键是一种包含共价电子、自由电子或磁性电子的混合键,因此,原子外层成键的价电子可以分为共价电子、自由电子和磁电子,非成键电子(简称非键电子)则视为具有化学惰性的离子实电子。其中,共价电子对结合能起主要作用,自由电子对导电、导热和塑性起主要作用,而磁电子对材料磁性起主要作用。
在OA理论中,用基本原子态φk(k=1,2,…,n)进行杂化(或叠加)所得到的准电子占据数(Quasi-Electron-Occupation ,QEO)来表征原子状态ψ:
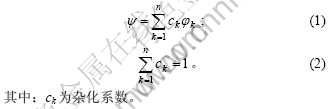
每一个基本态φk都遵循Pauli
不相容原理。设对金属Cu, 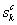 ,
,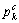 和
和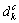 分别表示第k个基本原子态中s,p和d 轨道的共价电子数;
分别表示第k个基本原子态中s,p和d 轨道的共价电子数; 为自由的s态电子数;
为自由的s态电子数; 为非键的d电子数;
为非键的d电子数; (单位为0.1 nm)为已改进的Pauling单键半径[23];nc,nf和nv分别表示总的共价电子,自由电子和成键电子数,将算符
(单位为0.1 nm)为已改进的Pauling单键半径[23];nc,nf和nv分别表示总的共价电子,自由电子和成键电子数,将算符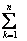 简写为∑,则Cu的单原子状态参数可以用以下公式来表达:
简写为∑,则Cu的单原子状态参数可以用以下公式来表达:

1.1.2 晶格常数方程
以下下标s的取值1,2等表示最近邻、次近邻等共价键,Gs为由晶体结构类型决定的常数,R为单键半径,β为Pauling的键参数[23],nc为总的共价电子数,Is为第s近邻键的等同键数,则晶格常数方程为:

1.1.3 结合能和势函数
多原子相互作用(Many-atom- interactions, MAI)势能函数以如下形式表达:

1.1.4 体弹性模量和线热膨胀系数
根据体弹性模量的定义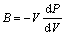 及势能与压强的关系
及势能与压强的关系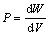 可以得到:
可以得到:
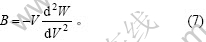
体积随温度的变化可以根据Debye-Grüneisen模型[24]确定的线热膨胀系数来确定:

1.2 计算程序
1.2.1 基本原子态
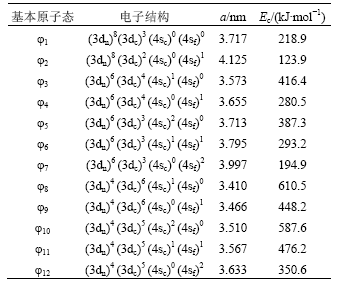
Eckardt[25]通过研究发现:由于存在强烈的s-p杂化,金属Cu外层未占据的p能级实际上已经等效于s能级。因此,p能级的电子可以视为s态电子。采用这种近似方法,本文计算10种基本原子态所对应的FCC结构晶体的晶格常数和结合能,结果如表1所示。其中:a为晶格常数,Ec为粘结能。
表1 金属Cu的基本原子态和相应FCC结构晶体的晶格常数和结合能
Table 1 Lattice constants and cohesive energies ofFCC-Cu in basic atom states
1.2.2 计算线路
基本原子态确定之后,将OA理论与CALPHAD确定晶格稳定参数的计算方法相结合,运用上述Debye-Grüneisen模型可以计算面心立方和亚稳液相Cu的原子状态和物理性质随温度的变化,计算线路如图1所示,其中星号“*”表示实验数据。以下按照计算程序分步进行详细说明。
第1步:假设Pauling单键半径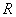 与晶格常数a随温度发生同比例的变化,而Debye温度*θD[26]不随温度变化,则在298.15 K时,根据FCC-Cu的*
与晶格常数a随温度发生同比例的变化,而Debye温度*θD[26]不随温度变化,则在298.15 K时,根据FCC-Cu的*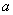 [24], *θD和R,由OA理论和Debye-Grüneisen模型可以计算FCC-Cu在0 K时的晶格常数和单键半径。
[24], *θD和R,由OA理论和Debye-Grüneisen模型可以计算FCC-Cu在0 K时的晶格常数和单键半径。
第2步:在0 K时,以晶格常数a=0.360 3 nm和结合能*Ec=336 kJ?mol-1 [26]为判据,对表1中的基本原子态进行筛选,发现φ4,φ9和φ12三态的线性组合可以在精度要求之内找到同时符合晶格常数和结合能标准的原子状态ψ,由结合能Ec得到原子势能εp,再根据势能函数求出体弹性模量B,最后得到0 K时FCC-Cu的Debye 温度、晶格常数、单键半径、结合能、电子结构、原子势能和体弹性模量,即*θD,a,R,*Ec,ψ,εp,B等。
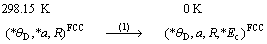
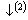
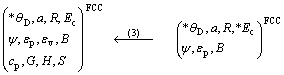
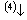

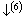

图1 确定FCC-Cu和Liquid-Cu原子状态和物理性质的计算线路图
Fig.1 Schematic procedure for determining atomic states and properties of FCC and Liquid pure Cu-metals
第3步:随着温度升高,FCC-Cu的价电子结构ψ几乎没有变化,所以,与第一原理热力学计算结果相似[27-28],实际计算中以0 K时的电子结构作为熔点以下任意温度的电子结构,但是,作为表征原子状态的另一个参数——单键半径将发生线性膨胀,因而,纯金属原子状态随温度的变化取决于单键半径随温度的变化,通过计算得到*θD,a,R,Ec,ψ,εp,εv,B,cp,G,H和S等参数随温度变化的情况。其中εv,cp,G,H和S分别代表原子振动能、恒压热容、Gibbs能、焓和熵等热力学参数。
第4步:在298.15 K时,根据CALPHAD方法确定的晶格稳定参数ΔGLiquid-FCC[4]得到Liquid-Cu的Gibbs能:
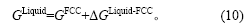
因为这一参数与Gibbs能参考态的选择无关,所以,(10)式同样适用于以0 K时的基态自由原子为参考态的情况,此时,有H(0 K)=-Ec(0 K)[29],并且:
 。 (11)
。 (11)
这里采用文献[10]中的近似公式来计算Liquid-Cu的Debye温度:
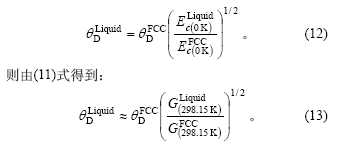
第5步:为了对Liquid-Cu的性质进行近似模拟,考虑其仍然保持短程有序的FCC结构[30],采用原子体积不变条件下[31]的等效晶体假设,即在原子体积完全相同的条件下,将低温Liquid-Cu视为等效的FCC晶体,其Grüneisen函数中的常数k 和Q0与FCC-Cu
结构的相同,根据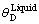 和
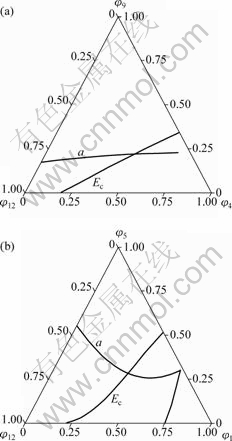
和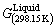 ,采用Debye-Grüneisen模型可以计算Liquid-Cu 0 K时的结合能
,采用Debye-Grüneisen模型可以计算Liquid-Cu 0 K时的结合能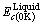 ,同时,根据金属Cu在熔点时的密度[32]得到
,同时,根据金属Cu在熔点时的密度[32]得到
平均原子体积,并转化为等效的晶格常数,由模型计算得到0 K时的晶格常数a,最终获得Liquid-Cu在0 K时的信息(θD,a,Ec)。
第6步:与第2步类似,在0 K时,根据Liquid-Cu的晶格常数a=0.367 0 nm和结合能Ec =323 kJ?mol-1,对表1中的基本原子态进行筛选,发现对φ1,φ5和φ12进行三态杂化可以找到同时满足晶格常数和结合能精度要求的原子状态ψ,然后,由结合能Ec得到原子势能εp和势能函数,从而求出体弹性模量B,最后获知(θD,a,R,Ec,ψ,εp,B)等参数。
第7步:与第3步类似,随着温度升高,Liquid-Cu的电子结构ψ不变,单键半径与晶格常数同比例地膨胀,由理论和模型计算同样得到(θD,a,R,Ec,ψ,εp,B,cp,G,H,S)等系列参数。
2 研究结果
2.1 原子状态
图2所示为FCC-Cu和Liquid-Cu以晶格常数和结合能为标准,在杂化三角形中找到等a线和等Ec线的交点,并根据交点对应的三态杂化成分确定的原子状态成分图,其杂化成分见表2。
(a) FCC-Cu; (b) Liquid-Cu
图2 FCC-Cu和Liquid-Cu三态杂化成分图
Fig.2 Composition positions of atomic states of FCCand Liquid pure Cu-metals
表2 FCC-Cu和Liquid-Cu三态杂化成分和性质
Table 2 Composition percents and properties of FCCand Liquid pure Cu-metals at 0 K

根据以上杂化成分确定FCC-Cu和Liquid-Cu的原子状态,得出其电子结构和单键半径为
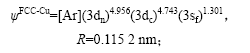
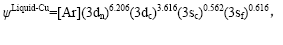

2.2 物理性质
2.2.1 势能函数
以nx和mx代表MAI势函数Wx(r)中的指数,r0为平衡状态最近邻原子键距,Ec为结合能,则FCC-Cu和Liquid-Cu的Wx(r)势如表3和图3所示。
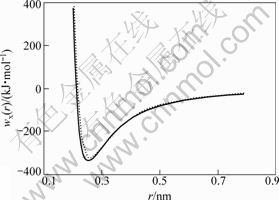
图3 FCC-Cu和Liquid-Cu的Wx(r)势能曲线
Fig.3 The potential energy curves of FCC and Liquid pure Cu-metals
表3 FCC-Cu和Liquid-Cu的Wx(r)势函数参数
Table 3 Parameters of Wx(r) potential function of FCC and Liquid Cu-metals

2.2.2 线热膨胀系数和体弹性模量
Debye-Grüneisen模型参数如表4所示,其中,线热膨胀系数中的实验数据来自文献[24]。图5给出了线热膨胀系数、晶格常数、原子体积、单键半径和体弹性模量随温度的变化关系。根据势函数可得到图4所示的体弹性模量随温度的变化曲线。
表4 FCC-Cu和Liquid-Cu的Debye-Grüneisen模型计算参数
Table 4 Constants of Debye-Grüneisen model for FCCand Liquid pure Cu-metals

2.2.3 原子动能和势能
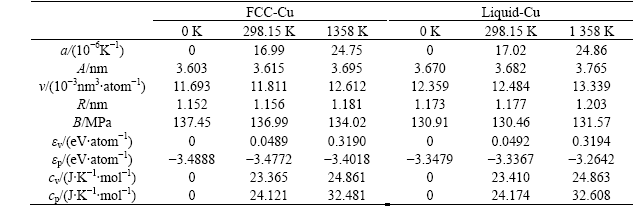
原子动能和势能随温度的变化关系见图5。为了更好地定量比较,将0 K, 298.15 K和熔点时的相关参数进行对比,结果见表5。
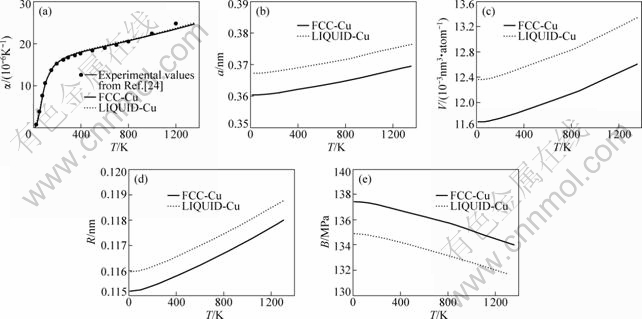
(a) 线热膨胀系数;(b) 晶格常数;(c) 原子体积;(d) 单键半径;(e) 体弹性模量
图4 FCC-Cu和Liquid-Cu的线热膨胀系数、晶格常数、原子体积、单键半径和体弹性模量随温度的变化
Fig.4 Relationship between temperature dependence and linear thermal expansion coefficients, lattice constants,
atomic volumes, single bond radiuses and bulk moduli of FCC-Cu and Liquid-Cu
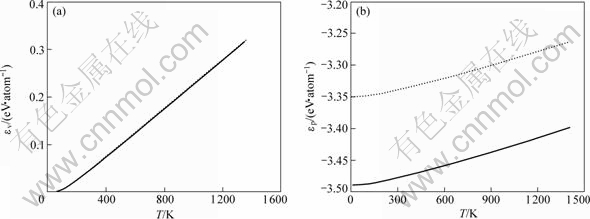
(a) 原子动能;(b) 原子势能
图5 FCC-Cu和Liquid-Cu的原子动能和势能随温度的变化
Fig.5 Temperature dependence of atomic vibration energy and potential energy of FCC-Cu and Liquid-Cu
表5 FCC-Cu和Liquid-Cu在0K,298.15 K和熔点时的物理性质对比
Table 5 Properties of FCC and Liquid pure Cu-metals at 0 K, 298.15 K and 1 358 K
3 分析和讨论
3.1 FCC-Cu的电子分布数
将运用OA理论方法所得电子结构与采用第一原理线性严密元胞法LRC [25]所得计算结果进行对比,结果见表6。
表6 不同方法研究FCC-Cu所得电子分布数的对比
Table 6 Atomic populations of FCC-Cu by various methods

由表6可知:采用OA理论方法所得的结果与采用第一原理所得的结果一致;此外,将采用OA理论方法所得计算结果与第一原理VASP程序[5]以及其他经验势函数[33]所得计算结果进行对比,结果见表7。
表7 不同方法研究FCC-Cu所得物理参数的对比
Table 7 Calculated properties of FCC-Cu using different methods
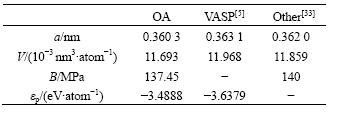
从表7可知:采用OA理论方法所得物理参数与由经验势函数所得结果更接近,与采用第一原理所得的结果差别较大。同时,由图5和表5可知:本文计算的线热膨胀系数随温度的变化关系与实验结果较吻合;晶格常数、原子体积和单键半径随温度发生同比例地膨胀;体弹性模量随温度上升而下降,但下降幅度不大。由图6和表5知:原子动能和原子势能均随温度升高而上升,并且动能随温度增加幅度是势能随温度增加幅度的3~4倍,在温度上升过程中,从外界吸收的热量主要用于增加原子的动能。
3.2 Liquid-Cu
对SGTE纯单质数据库中熔点以下的亚稳液相Cu采用原子体积不变条件下的等效晶体假设,对这种假设有效性的检验主要通过与实验数据的对比来说明。根据实验结果可知:金属Cu熔点以上的液相热容恒等于熔点的热容[34],并且当亚稳液相在熔点转变为稳定液相时不发生相变,它们的恒压热容Cp相等,所以,本文计算的Liquid-Cu熔点时的热容即为稳定液相的热容。表8所示为熔点温度时FCC-Cu和Liquid-Cu的热容计算值与SGTE数据库结果,并与实验值进行误差对比。可见,本文计算值与实验值的误差较小,特别是液相热容与实验数据较吻合,从而证明所作假设是有效的。
表8 1 358 K时FCC-Cu和Liquid-Cu的热容计算值与SGTE数据库结果及实验数据的比较
Table 8 Isobaric heat capacity of FCC and Liquid Cu at 1 358 K

对电子结构进行对比分析发现:Liquid-Cu的自由电子数0.616比FCC-Cu的1.301减少了近1半,与液相电导率下降或电阻率增大的幅度2.04[35]一致。表9所示为熔点温度时电阻率的实验结果。
表9 熔点时FCC-Cu和Liquid-Cu的自由电子数与电阻率的比较
Table 9 Comparison between the number of free electrons and electrical resistivity at melting point of FCC
and Liquid Cu

对比固液相电子结构还发现:固相向液相转变时,原子最外层的自由电子和原子间的共价电子均向非键电子转移,方向性强的共价d电子向球对称的共价s电子转移,从而削弱了原子之间配位的方向性,增加了原子之间配位的自由性。电子结构的转变使Liquid-Cu单键半径公式(3)中的共价d电子在总价电子数中的比例减小,引起原子单键半径和原子体积 增大。
4 结 论
a. 在合金系统科学(SSA)框架下,运用纯金属单原子(OA)理论对FCC-Cu的原子状态,原子势能、原子动能、原子体积、体弹性模量和热膨胀系数等物理参数随温度的变化进行研究,发现电子结构的计算结果与采用第一原理所得结果一致;单键半径随温度升高发生膨胀;线热膨胀系数与实验值较吻合;体弹性模量随温度上升而缓慢下降;原子动能随温度增加的幅度是势能随温度增加幅度的3~4倍,体系吸收的热量主要用于增加原子动能。
b. 采用原子体积不变的等效晶体假设,对SGTE纯单质数据库中熔点以下的亚稳液相Cu进行OA理论研究,发现采用这种模拟方法得到的稳定液相的恒压热容与实验值的误差小,与实验结果较吻合。
c. 对FCC-Cu和Liquid-Cu原子状态的OA理论进行研究发现,固相向液相转变时,原子最外层的自由电子和原子间的共价电子均向非键电子转移,同时方向性强的共价d电子向球对称的共价s电子转移,电子结构的转变降低液相的导电性,削弱液相原子配位的方向性,导致共价d电子在总价电子数中的比例减小,引起原子单键半径和体积增大。
参考文献:
[1] Kaufman L, Bernstein H. Computer calculation of phase diagram[M]. New York: Academic Press Inc, 1970.
[2] Saunders N, Miodownik A P. CALPHAD (Calculation of Phase Diagrams): A comprehensive guide[M]. New York: Pergamon, 1998.
[3] Saunders N, Miodownik A P, Dinsdale A T. Metastable lattice stabilities for the elements[J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 1988, 12: 351-374.
[4] Dinsdale A T. SGTE data for pure elements[J]. CALPHAD, 1991, 15(4): 317-425.
[5] Wang Y, Curtarolo S, Jiang C, et al. Ab initio lattice stability in comparison with CALPHAD lattice stability[J]. CALPHAD, 2004, 28: 79-90.
[6] XIE You-qing, TAO Hui-jin, PENG Hong-jian, et al. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl2 type alloys[J]. Physica B, 2005, 366: 17-37.
[7] XIE You-qing. A new potential function with many-atom interactions in solid[J]. Science in China: Series E, 1993, 36(1): 90-99.
[8] XIE You-qing. Relationship of Lennard-jones potential and Morse potential with Wx(r) potential[J]. Transactions of Nonferrous Metals Society of China, 1994(4): 63-66.
[9] XIE You-qing, ZHANG Xiao-dong, ZHAO Li-yin, et al. Electronic structure and properties of Cu metal[J]. Science in China: Series A, 1993, 36(4): 487-494.
[10] XIE You-qing, MA Liu-yin, ZHANG Xiao-dong, et al. Microstructure and properties of Cu-Ni alloys[J]. Science in China: Series A, 1993, 36(5): 612-623.
[11] XIE You-qing. Electronic structure and properties of pure iron[J]. Acta Metallurgica Materialia, 1994, 42(11): 3705-3715.
[12] XIE You-qing. Atomic energies and gibbs energy functions for Ag-Cu alloys[J]. Science in China: Series E, 1998, 41(2): 146-156.
[13] XIE You-qing, ZHANG Xiao-dong. Atomic volumes and volume functions for Ag-Cu alloys[J]. Science in China: Series E, 1998, 41(2): 157-168.
[14] XIE You-qing, ZHANG Xiao-dong. Electronic structure of Ag-Cu alloys[J]. Science in China: Series E, 1998, 41(3): 225-236.
[15] XIE You-qing, ZHANG Xiao-dong. Phase diagram and thermodynamic properties of Ag-Cu alloys[J]. Science in China: Series E, 1998, 41(4): 348-356.
[16] XIE You-qing, PENG Kun, LIU Xin-bi. Influences of xTi/xAl on atomic states, lattice constants and potential-energy planes of ordered FCC TiAl-type alloys[J]. Physica B, 2004, 344: 5-20.
[17] XIE You-qing, LIU Xin-bi, PENG Kun, et al. Atomic states, potential energies, volumes, stability, and brittleness of ordered FCC TiAl3-type alloys[J]. Physica B, 2004, 353: 15-33.
[18] XIE You-qing, PENG Hong-jian, LIU Xin-bi, et al. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti3Al-type alloys[J]. Physica B, 2004, 362: 1-17.
[19] YU Fang-xin, XIE You-qing, NIE Yao-zhuang. Electronic structure of Au-Cu alloys[J]. Transactions of the Nonferrous Metals Society of China, 2004, 14(6): 1041-1049.
[20] 谢佑卿. Au-Cu合金系中无序和有序相的晶格常数[J]. 金属学报, 1998, 34(12): 1233-1242.
XIE You-qing. Lattice constants of disordered and ordered phases in the Au-Cu system[J]. Acta Metallurgica Sinica, 1998, 34(12): 1233-1242.
[21] 谢佑卿, 张晓东. Au-Cu合金的微观结构和性质[J]. 金属学报: A辑, 1994, 30(12): 531-539.
XIE You-qing, ZHANG Xiao-dong. Microstructure and properties of Au-Cu alloys[J]. Acta Metallurgica Sinica, 1994, 30(12): 531-539.
[22] GUO Yi-qing, YU Rui-huan, ZHANG Rui-lin, et al. Calculation of magnetic properties and analysis of valence electronic structures of LaT13-xAlx(T=Fe, Co) compounds[J]. Journal of Physical Chemistry B, 1998, 102(1): 9-16.
[23] Pauling L. Nature of the chemical bond[M]. Ithaca: Cornell University Press, 1960.
[24] Kirby R K, Hahn T A, Rothroch B D. Thermal expansion[C]// Gray D E. American Institute of Physics Handbook. New York: McGraw-Hill Book Company, 1972: 119-138.
[25] Eckardt H, Fritsche L, Noffke J. Self-consistent relativistic band structure of the noble metals[J]. J Phys F: Met Phys, 1984, 14: 97-112.
[26] Kittel C. Solid state physics[M]. New York: John Wiley and Sons Inc, 1976.
[27] Ozolin V, Wolverton S C, Zunger A. Cu-Au, Ag-Au, Cu-Ag, and Ni-Au intermetallics: First-principles study of temperature- composition phase diagrams and structures[J]. Phys Rev B, 1998, 57(11): 6427-6443.
[28] Wei S H, Mbaye A A, Ferreira L G, et al. First-principles calculations of the diagrams of noble metals: Cu-Au, Cu-Ag and Ag-Cu[J]. Phys Rev B, 1987, 36(8): 4163-4185.
[29] 陈景榕, 李承基. 金属与合金中的固态相变[M]. 北京: 冶金工业出版社, 1997: 8-10.
CHEN Jing-rong, LI Cheng-ji. Phase transitions of solids in metals and alloys[M]. Beijing: Metallurgical Industry Press, 1997: 8-10.
[30] XIE You-qing, DENG Yong-ping, LIU Xin-bi. Electronic structure and physical properties of Cr, Mo, W metal[J]. Transactions of Nonferrous Metals Society of China, 2003, 13(5): 1102-1107.
[31] Barkonyi I, Elbert H, Liechtenstein A I. Electronic structure and magnetic susceptibility of the different structural modifications of Ti, Zr and Hf metals[J]. Physcal Review B, 1993, 48: 7841-7849.
[32] Weast R C. CRC handbook of chemistry and physics, 70th ed[M]. Florida: CRC Press Inc, 1990: B-216.
[33] Zhang Z J. Calculation of the properties of some metals and alloys[J]. Journal of Physics: Condens Matter, 1998, 10: L495-L499.
[34] Chase M W. NIST-JANAF thermochemical tables fourth edition part I[M]. Gaithersburg: National Institute of Standards and Technology, 1998.
[35] Cusack N E. The electronic properties of liquid metals[J]. Reports on Progress in Physics, 1963, 26(1): 361-409.
收稿日期:2006-05-15
基金项目:国家自然科学基金资助项目(No.50271085, 50471058)
作者简介:陶辉锦(1976-),男,湖南醴陵人,博士研究生,从事计算材料研究
通讯作者:陶辉锦,男,博士研究生;电话:0731-8879287(O);E-mail: taohuijin@hotmail.com