静态磁场对分离结晶中熔体流动的影响
来源期刊:中国有色金属学报(英文版)2015年第3期
论文作者:彭 岚 龚 欢
文章页码:936 - 943
关键词:分离结晶;静态磁场;热毛细-浮力对流;数值模拟;CdZnTe
Key words:detached solidification; static magnetic field; thermocapillary-buoyancy convection; numerical simulation; CdZnTe
摘 要:采用三维数值模拟手段对微重力条件下熔体内部的热毛细对流以及常重力条件下熔体内部的热毛细-浮力对流进行研究。模拟中选取无磁场、施加轴向磁场和施加勾形磁场3种不同的磁场条件进行对比。模拟结果表明,轴向磁场和勾形磁场都能够有效地抑制熔体内部的流动和温度波动;在相同磁场强度下,轴向磁场的抑制效果比勾形磁场更为显著。此外,还对重力条件下熔体内部热毛细-浮力对流的失稳机理进行分析,以研究磁场对临界Ma数的影响。
Abstract: A series of three-dimensional numerical computations were conducted to understand the effects of different static magnetic fields on thermal fluctuation and melt flow during the detached solidification of CdZnTe. Numerical calculations were carried out by three different configurations of magnetic field: without magnetic field, with an axial magnetic field (AMF) and with a cusp-shaped magnetic field (CMF). The results reveal that the magnetic fields can effectively suppress the melt flow and thermal fluctuation and the suppression effect of the AMF is stronger than that of the CMF. Besides, the physical mechanism of thermocapillary-buoyancy convection instability was discussed and the effects of magnetic field on the critical Marangoni number were also obtained.
Trans. Nonferrous Met. Soc. China 25(2015) 936-943
Lan PENG, Huan GONG
Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Ministry of Education,
College of Power Engineering, Chongqing University, Chongqing 400044, China
Received 8 April 2014; accepted 8 August 2014
Abstract: A series of three-dimensional numerical computations were conducted to understand the effects of different static magnetic fields on thermal fluctuation and melt flow during the detached solidification of CdZnTe. Numerical calculations were carried out by three different configurations of magnetic field: without magnetic field, with an axial magnetic field (AMF) and with a cusp-shaped magnetic field (CMF). The results reveal that the magnetic fields can effectively suppress the melt flow and thermal fluctuation and the suppression effect of the AMF is stronger than that of the CMF. Besides, the physical mechanism of thermocapillary-buoyancy convection instability was discussed and the effects of magnetic field on the critical Marangoni number were also obtained.
Key words: detached solidification; static magnetic field; thermocapillary-buoyancy convection; numerical simulation; CdZnTe
1 Introduction
The technological potential of CdZnTe is great due to its excellent physical properties in the area of medical imaging and photorefractive sensors. Furthermore, CdZnTe is a tricky material in terms of crystal growth, the traditional available growth techniques are unsatisfactory because of its thermal sensitivity. Since the first observation of detachment on skylab in 1974 by accident, it attracted much attention for its remarkable performance in crystallography [1]. As described in Ref. [2], since the absence of the stress produced by differential thermal contraction of the crystal and ampoule, the dislocation density is tremendously reduced. Based on the model proposed by DUFFAR et al [3-5], detached solidification can be achieved by applying a gas pressure between the ampoule and the crystal.
However, melt flow still has a fundamental influence on the crystal quality in detached solidification. To obtain the high-quality crystal, the accurate control of melt flow and thermal fluctuation is essential [6,7].
A substantial amount of progress has been made in the past decades in understanding the influence of magnetic fields on the melt flow and thermal distribution in the crystal growth [8-10]. LIU et al [11,12] studied the effects of magnetic field on the turbulent convection and thermal fluctuation. They found that the cusp-shaped magnetic field (CMF) provides stronger suppression effect on thermal instability than the transverse magnetic field (TMF). JABER et al [3] indicated that the melt flow can be effectively suppressed by the axial and rotating magnetic field during GeSi crystal growth. SADRHOSSEINI and SEZAI [14] found that the suppression effect of magnetic field on the melt flow is enhanced with the increase of Ha. CEN et al [15] compared the effect of the static magnetic field on the melt flow and found that the axial magnetic field is more effective in suppressing the convection than the cusp magnetic field.
As the CdZnTe melt is electrically conductive, the application of magnetic field is identified as an effective way to weaken the melt flow. PENG et al [16] conducted a two-dimensional global simulation of detached solidification under a cusp magnetic field and the results exhibited that the cusp magnetic field has a suppression effect on the melt flow. LI et al [17] studied the effects of geometric parameters and axial magnetic field on thermocapillary-buoyancy convection during detached solidification. The results indicated that the inhibition effect of axial magnetic field is enhanced as the Ha increases.
In this work, to make a comprehensive analysis of the influence of static magnetic field on the flow behavior and the temperature fluctuation of molten CdZnTe in detached solidification, the three-dimensional numerical simulations were performed for three configurations: without magnetic field, with axial magnetic field (AMF) and with cusp-shaped magnetic field (CMF). Meanwhile, the evolution of flow pattern and the physical mechanism of unstable Marangoni convection were explored. And magnetohydrodynamic (MHD) effects on the critical Marangoni number (Ma) were also discussed.
2 Physical and mathematical models
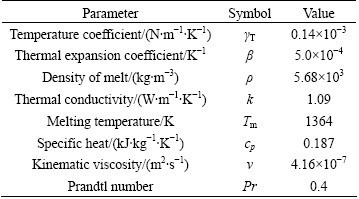
The schematic diagrams for three configurations: without magnetic field, with AMF and with CMF are plotted in Fig. 1. In addition, the cusp-shaped magnetic field adopted in the simulation was produced by two identical solenoids carrying equal but counter-rotating currents [18]. The aspect ratio A (height/radius) of the crucible equals 1, and the non-dimensional width of the gas gap (S) equals 0.1. The physical properties of CdZnTe are listed in Table 1.
The main assumptions adopted in the simulation are summarized as follows: 1) The CdZnTe melt is incompressible Newtonian fluid; 2) The free surfaces of the gas gap and the top of melt are adiabatic; 3) All boundaries are electric insulators; 4) The induced field caused by electromagnetic field is ignored; 5) On the free surface, the thermocapillary force is taken into account, and at other solid-liquid boundaries, the no-slip condition is applied; 6) The surface tension is linear function of the temperature.
Table 1 Physical properties of CdZnTe melt [19,20]
Based on the above assumptions, the melt flow is described by the dimensionless three dimensional continuity, Navier-Stokes and energy equations are in the domain 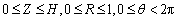 .
.
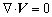 (1)
(1)
 (2)
(2)
 (3)
(3)
where V, P and Θ are non-dimensional velocity, pressure and temperature, respectively. The dimensional scales of the time, the velocity, the pressure and the temperature are as follows:
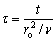 ,
, 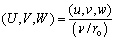 ,
, 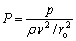 ,
, 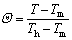
where ro is the radius of ampoule; Th is the temperature of ampoule wall; U, V, W are three velocity components.
Other parameters are Grashof number 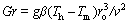 , Prandtl number Pr=v/a. Special note is that under the condition of microgravity, the gravity acceleration (g) can be considered zero, thus, the term of buoyancy is negligible.
, Prandtl number Pr=v/a. Special note is that under the condition of microgravity, the gravity acceleration (g) can be considered zero, thus, the term of buoyancy is negligible.
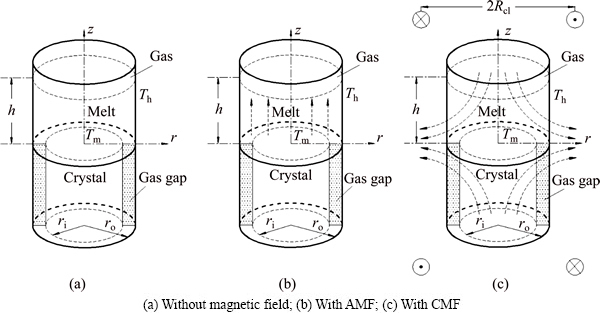
Fig. 1 Physical model of simulation system
According to the Ohm’s law, the electric current (J) induced by the interaction of the magnetic field and the melt flow can be expressed as  where σ is electric conductivity of the melt, ψ is stream function and B is magnetic field intensity. The Kirchhoff’s current law,
where σ is electric conductivity of the melt, ψ is stream function and B is magnetic field intensity. The Kirchhoff’s current law,  can yield the equation for the stream function
can yield the equation for the stream function 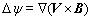 . For CMF, the magnetic field intensity
. For CMF, the magnetic field intensity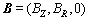 , and the Lorentz force F can be calculated as follows:
, and the Lorentz force F can be calculated as follows:
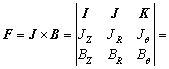
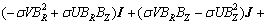
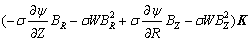 (4)
(4)
where 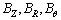 are the non-dimensional components of magnetic field in three coordinate directions and
are the non-dimensional components of magnetic field in three coordinate directions and  are the non-dimensional three components of electric current. For AMF, the magnetic field intensity B=(BZ, 0, 0). The equation for Lorentz force F expressed above is suit for the case of AMF as well.
are the non-dimensional three components of electric current. For AMF, the magnetic field intensity B=(BZ, 0, 0). The equation for Lorentz force F expressed above is suit for the case of AMF as well.
The calculating results showed that for CMF, Lorentz force (F) can be expressed by three components:
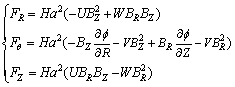 (5)
(5)
where f is electric potential.
For AMF, Lorentz force F has two components in R and θ axes direction:
 (6)
(6)
The Hartmann number is defined as  , where b0 is the axial component of magnetic density at the center of the crystal-crucible interface and is chosen as the reference parameter.
, where b0 is the axial component of magnetic density at the center of the crystal-crucible interface and is chosen as the reference parameter.
The corresponding boundary conditions are expressed as follows.
On the top surface (Z=H, 0≤R<1, 0≤θ<2π):
 (7)
(7)
At the solidification interface (Z=0, 0
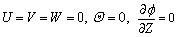 (8)
(8)
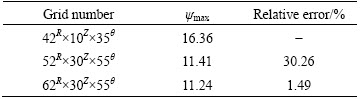
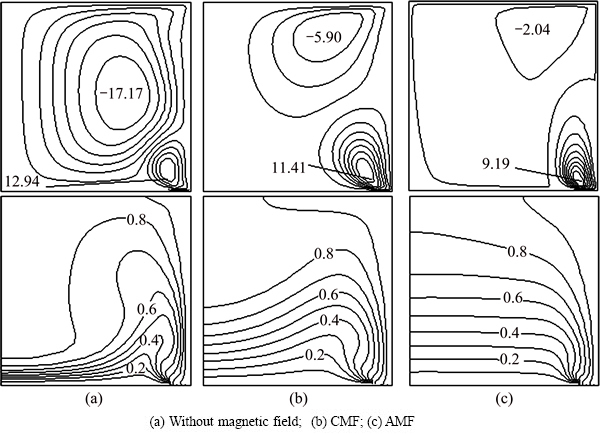
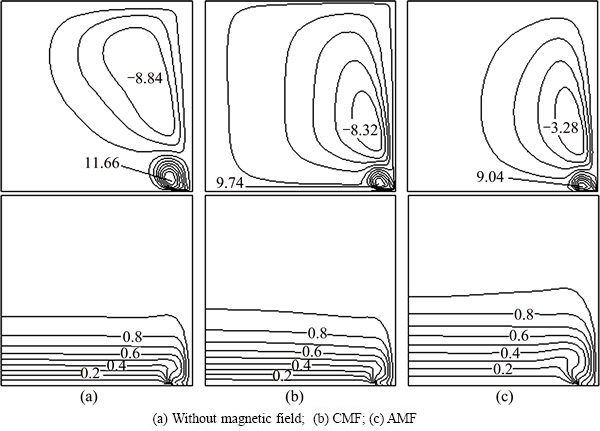
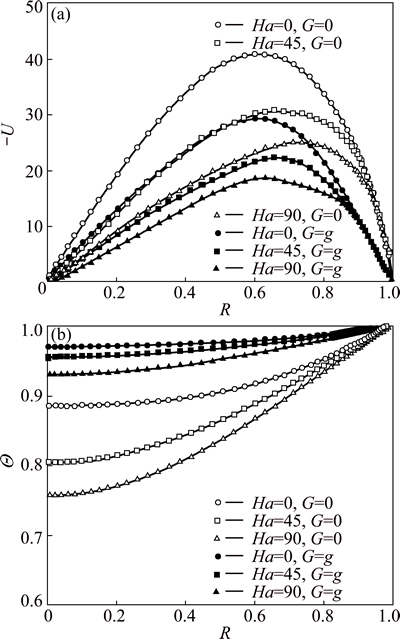
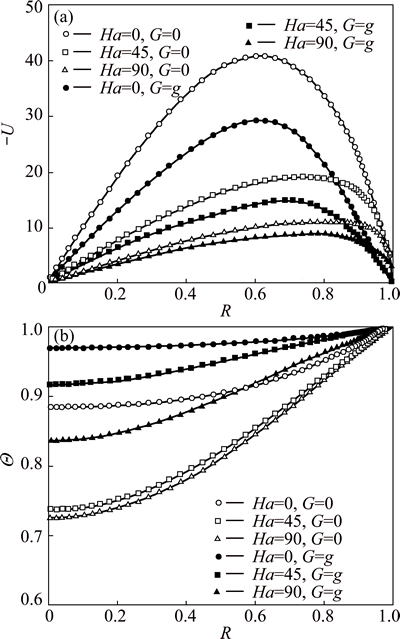
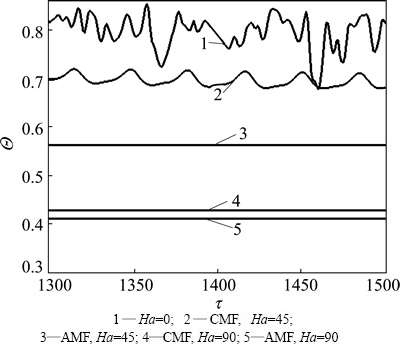
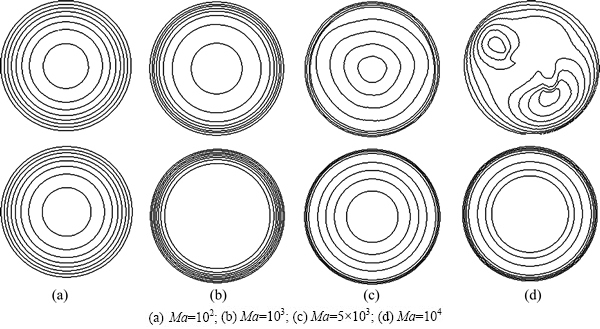
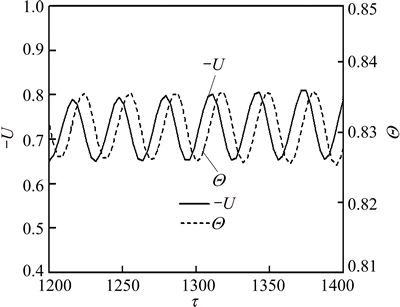
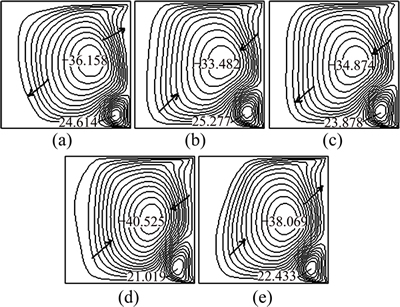
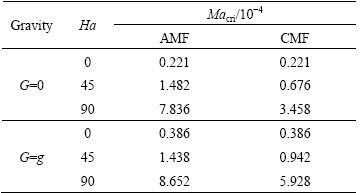
At the gas-melt interface (Z=0, Ri At the ampoule wall (R=1, 0≤Z≤H, 0≤θ<2π): The initial conditions (τ=0): The variables are non-dimensionalized as The fundamental equations and boundary conditions are discretized by the finite-difference method. The central difference approximation is applied to the diffusion terms while the quick scheme is used for the convective terms. The simple algorithm is adopted to deal with the pressure coupling. An important issue for the quality of the numerical simulations is the choice of the grid. In this study, non-uniform staggered grid of 52R×30Z×55θ is used. In order to check the grid convergence, simulations with three different meshes, i.e., 42R×10Z×35θ, 52R×30Z×55θ, 62R×30Z×55θ, are performed for the case of CMF and the maximum values of stream function are evaluated as shown in Table 2. Consequently, it turns out that the grid selected in the work is sufficient for the accurate simulation. For the case of AMF, sufficient grid convergence is confirmed by the same method [21]. Table 2 Validation of grid convergence 3 Results and discussion 3.1 MHD effects on time-averaged fields of velocity and temperature Owing to the temperature difference, there is surface tension gradient along the gas-melt interface, which can cause the melt flow. This surface-tension- driven convection is known as Marangoni convection, which can be significant in microgravity. For the case of small temperature difference, the flow in the melt is steady and axisymmetric. Figure 2 presents the variation of melt flow and thermal field in the melt domain at Ma=103 under different magnetic fields in microgravity. The value of stream function contours in Fig. 2 reveal two major vortices. In the absence of magnetic field, the flow cells occupy the whole melt area and the maximum value of stream function of the anticlockwise toroidal roll cell (the upper one) is 17.17, and that of clockwise toroidal roll cell is 12.94 as shown in Fig. 2(a). Meanwhile, the isotherm is seriously distorted when Ha=0. Figure 2(b) describes the distribution of the value of stream function and isotherms in the presence of CMF. Compared with Fig. 2(a), the value of stream function decreases and the isotherm has a tendency to be uniform. When the AMF is applied, the decreased degree of the value of stream function increases and the isotherms are almost equal spacing distribution. This indicates that the inhibition effect of AMF is stronger than that of CMF at the same reference magnetic field intensity. Under the condition of the ground, buoyancy and thermocapillary forces are coupled to cause thermocapillary–buoyancy convection, which makes the melt flow become more complex. Compared with the case in microgravity, the center of toroidal roll cells moves down and isotherms concentrate on the bottom of the melt as shown in Fig. 3. Without magnetic field, the maximum value of stream function of the anticlockwise toroidal roll cell (the upper one) is 8.84, and that of clockwise toroidal roll cell is 11.66 as shown in Fig. 3(a). This suggests that the strength is weakened since the existence of gravity can stabilize the melt flow. Both the applications of CMF and AMF have an inhibition effect on the thermocapillary–buoyancy convection. But the suppression effect of magnetic field on the melt flow is not as remarkable as the case in microgravity. This implies that the stronger the melt flows, the more significant the inhibition effect of magnetic field is. Fig. 2 Streamlines and isotherms on R-Z plane at Ma=103, Ha=45 and G=0, δψ = ψmax/10, Fig. 3 Streamlines and isotherms on R-Z plane at Ma=103, Ha=45 and G=g, δψ=ψmax/10, 3.2 MHD effects on velocity and temperature distributions on free surfaces The velocity and temperature distributions on the upper free surface at θ=0 with CMF and AMF are plotted in Fig. 4 and Fig. 5, respectively. As shown in Fig. 4 and Fig. 5, whether in microgravity or under the condition of gravity, the velocity on the upper free surface presents a parabolic distribution along the crucible radius. In the absence of magnetic field, the parabolic trend is steep, while, in the presence of magnetic field, the velocity distribution tends to be flat. It is noteworthy that when the Ha increases from 0 to 45, the melt velocity decreases sharply, while the Ha increases further, the velocity decreases slightly. This implies that when Ha=90, the melt flow can be effectively suppressed, while the suppression effect will not be enhanced greatly with the further increase of magnetic field intensity. Moreover, under the same magnetic field, velocity on the upper free surface in microgravity is larger than that under the gravity condition. This result is consistent with the comparison of stream function described in Fig. 2 and Fig. 3, illustrating that the gravity can stabilize the melt flow. Meanwhile, the non-linearity of temperature is reduced since the convection heat transfer is weakened by the application of magnetic field. Besides, the situation on the free surface of gas gap is basically the same and will not be repeated in this work. Fig. 4 Distributions of velocity (a) and temperature (b) on upper free surface at Ma=102 with CMF Fig. 5 Distributions of velocity (a) and temperature (b) on upper free surface at Ma=102 with AMF 3.3 MHD effects on time evolutions of temperature fluctuation The comparisons of the temperature evolution at the reading point for the three configurations are plotted in Fig. 6. In the absence of magnetic field, many peaks appear in the different frequency bands. This means that the system is in a state of instability and the temperature fluctuates without regularity. For the CMF configuration, the temperature variation has a strong dependence on the Ha. When Ha=45, temperature at the reading point oscillates with constant amplitude and the amplitude of the temperature oscillation decreases dramatically. As Ha increases to 90, the temperature fluctuation disappears and temperature distribution is constant in time. However, with the AMF of Ha=45, temperature is stable, indicating that the melt flow is stabilized by the AMF. And the temperature tends to be more stable with the increase of the AMF intensity. This is the further proof that the suppression effect of AMF is superior to that of CMF. Fig. 6 Effects of magnetic field on temperature fluctuation at reading point for Ma=104 The fundamental reason lies in the magnetic structure of CMF. The CMF consists of axial components and radial components. The directions of axial components generated by two coils are opposite, while the radial components are the same. As a consequence, the magnetic structure of CMF is inhomogeneous. And the strength of magnetic field at reference point (at the center of the crystal-crucible interface) is stronger than most spots in the melt area. Meanwhile, the intensity of AMF is uniform, which equals the intensity of reference point. Therefore, AMF has more remarkable suppression effect on the melt flow. 3.4 Unstable Marangoni convection Under the condition of small temperature difference, the convection is gentle and the temperature distribution exhibits a conduction-dominated pattern that the isotherms on the upper free surface are concentric circles at Ma=102, as shown in Fig. 7(a). In the presence of CMF (Ha=45), the temperature gradient increases with the Marangoni number, especially in the vicinity of the crucible sidewall at Ma=103. As the Marangoni number increases further, the isotherm distribution has a tendency to be deformed at Ma=5×103, and finally the convection becomes unstable, hence the isotherms become irregular and twisty at Ma=104. It is worth noting that for the case of instability, the temperature distribution on the upper free surface is transient. While for the AMF of Ha=45, the isotherms on the upper free surface are concentric circles even at Ma=104, indicating that the melt flow is stable due to the suppression effect of AMF. This is the further proof that the AMF provides stronger suppression effect on the thermal instability than CMF at the same reference magnetic field intensity. The convection is oscillatory, and the segment of non-dimensional velocity and temperature at the observation point, for example, R=0.5, Z=0.2, θ=0, is shown in Fig. 8. Besides, the evolution of flow pattern during a period is described in Fig. 9. From Fig. 8 and Fig. 9, the physical mechanism of the unstable Marangoni convection can be explained as follows: When Ma exceeds the critical value, the intensity of vortex is enhanced distinctly, especially the thermocapillary convection plays a dominant role. Thus, there will be disturbance between the upper and lower roll cells. When the disturbance spreads down, the intensity of lower vortex is enhanced, leading to the increase of flux of cold melt into the gas-melt interface. Hence, the temperature of gas-melt interface drops, which lags behind the velocity as shown in Fig. 8. The decrease of temperature results in the increase of flow resistance, thus, the melt flow is weakened. Owing to the decrease of melt velocity, the temperature of melt- crystal interface rises subsequently, which decreases the flow resistance. Thereby, the velocity begins to increase. And the fundamental reason can be attributed to the existence of a hysteretic phenomenon between the velocity and temperature. Fig. 7 Distributions of isotherms on upper free surface with CMF (upper), with AMF (lower), G=g, Fig. 8 Segment of non-dimensional velocity and temperature at Ma=8×103, G=g Fig. 9 Evolution of flow pattern on R-Z plane during a period at Ma=3.8×103, G=g When the steady flow transits into unstable Marangoni convection, there must be a critical point. A comparison is carried out to make clear the effects of AMF and CMF on the critical Ma at H=1 and B=0.1 with the linear extrapolation method as shown in Table 3. It is easy to found that the critical Ma increases as the magnetic field is enhanced, which leads to more stable flow pattern. Table 3 Critical Ma numbers at H=1 and B=0.1 4 Conclusions 1) Both the CMF and AMF have suppression effects on the melt flow and thermal fluctuation. The suppression effect of magnetic fields is enhanced with the increase of Ha, while for Ha=90, the melt can be well suppressed. 2) In the same circumstance, the intensity of thermocapillary convection is stronger than that of thermocapillary-buoyancy convection. This is owing to the existence of gravity which can stabilize the melt flow. 3) For the same Ma, the AMF provides stronger suppression effect than the CMF at the same reference magnetic field intensity. 4) The physical mechanism of unstable Marangoni convection lies in the hysteretic phenomenon between velocity and temperature. Besides, the application of magnetic field can increase the critical Ma. References [1] WITT A F, GATOS H C, LICHTENSTEIGER M, LAVINE M C, HERMAN C J. Crystal growth and steady-state segregation under zero gravity: InSb [J]. Journal of the Electrochemical Society, 1975, 122(2): 276-283. [2] REGAL L L, WILCOX W R. A review of detached solidification in microgravity [J]. Microgravity Science and Technology, 1999, 14: 152-166. [3] DUFFAR T, SERRANO M D, MOORE C D. Bridgman solidification of GaSb in space [J]. Journal of Crystal Growth, 1998, 192: 63-72. [4] DUFFAR T, DUSSERRE P, PICCA F, LACROIX S, GIACOMETTI N. Bridgman growth without crucible contact using the dewetting phenomenon [J]. Journal of Crystal Growth, 2000, 211: 434-440. [5] FIEDERLE M, DUFFAR T, BABENSOVL V, BENZ K W, DUSSERRE P, CORREGIDOR V, DIEGUEZ E, DELAYE P, ROOSEN G, CHEVRIER V, LAUNAY C. Dewetted growth of CdZnTe in microgravity (STS-95) [J]. Crystal Research and Technology, 2004, 39(6): 481-490. [6] SINNO T, DOMBERGER E, AMMON W V, BROWN R A, DUPRET F. Defect engineering of Czochralski single-crystal silicon [J]. Materials Science and Engineering R, 2000, 28: 149-198. [7] TOMZIG E, VIRBULIS J, AMMON W V, GELFGAT A Y, GORBUNOV L. Application of dynamic and combined magnetic fields in the 300 mm silicon single-crystal growth [J]. Materials Science in Semiconductor Processing, 2003, 5: 347-351. [8] CHENG Cong-qian, HUANG Ming-liang, ZHAO Jie, XUE Dong-feng. Effect of uniform magnetic field on crystallization of intermetallic compound layers between Cu and liquid SnZn alloys [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2312-2319. [9] CHEN Rui-run, YANG Jie-ren, DING Hong-sheng, HUANG Feng, SU Yan-qing, GUO Jing-jie, FU Heng-zhi. Effect of configuration on magnetic field in cold crucible using for continuous melting and directional solidification [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 404-410. [10] LI Mi, PENG Bing, CHAI Li-yuan, WANG Ji-ming, PENG Ning, YAN Huan. Element distribution of high iron-bearing zinc calcines in high gradient magnetic field [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2261-2267. [11] LIU X, LIU L J, LI Z Y, WANG Y. Effects of static magnetic fields on thermal fluctuations in the melt of industrial CZ-Si crystal growth [J]. Journal of Crystal Growth, 2012, 360: 38-42. [12] LIU X, LIU L J, LI Z Y, WANG Y. Effects of cusp-shaped magnetic field on melt convection and oxygen transport in an industrial CZ-Si crystal growth [J]. Journal of Crystal Growth. 2012, 354: 101-108. [13] JABER T J, SAGHIR M Z, VIVIANI A. Three-dimensional modeling of GeSi growth in presence of axial and rotating magnetic fields [J]. European Journal of Mechanics B/Fluids, 2009, 28: 214-223. [14] SADRHOSSEINI H, SEZAI I. Effect of magnetic field on radial dopant segregation in crystal growth by traveling heater method [J]. International Journal of Thermal Sciences, 2010, 49: 2419-2427. [15] CEN X R, LI Y S, ZHAN J M. Three dimensional simulation of melt flow in Czochralski crystal growth with steady magnetic fields [J]. Journal of Crystal Growth, 2012, 340: 135-141. [16] PENG Lan, ZHOU Lin-min, LI You-rong, WEN Jing-xiong. Effect of cusp magnetic field on CdZnTe crystal growth by detached solidification [J]. Journal of Engineering Thermophysics, 2012, 33: 565-568. (in Chinese) [17] LI Zhen, PENG Lan, LI You-rong. Effects of geometric parameters and axial magnetic field on Buoyant-Thermocapillary convection during detached solidification [J]. Transactions of Nonferrous Metals society of China, 2014, 24(5): 1512-1520. [18] LIANG X A, JIN W Q, PAN Z L. Progress of magnetic field application in crystal growth [J]. Journal of Inorganic Materials, 1999, 14: 833-839. [19] PARFENIUK C, WEINBERG F, SAMARASEKERA I V, SCHVEZOV C, LI L. Measured critical resolved shear stress and calculated temperature and stress fields during growth of CdZnTe [J]. Journal of Crystal Growth, 1992, 119: 261-270. [20] ZHANG G D, LIU J C, LI J. Influence of the graphite film plating on the inner wall of quartz crucible on the thermal stress in CdZnTe crystal prepared by Bridgman method [J]. Acta Metallurgica Sinca, 2007, 43: 1071-1076. [21] PENG L, MENG H Y,LI Y R,LI Z. Axial magnetic field influence on thermocapillary convection in detached solidification under microgravity [J]. Microgravity Science and Technology, 2011, 23: 141-147. 彭 岚,龚 欢 重庆大学 动力工程学院 低品位能源利用技术及系统教育部重点实验室,重庆 400044 摘 要:采用三维数值模拟手段对微重力条件下熔体内部的热毛细对流以及常重力条件下熔体内部的热毛细-浮力对流进行研究。模拟中选取无磁场、施加轴向磁场和施加勾形磁场3种不同的磁场条件进行对比。模拟结果表明,轴向磁场和勾形磁场都能够有效地抑制熔体内部的流动和温度波动;在相同磁场强度下,轴向磁场的抑制效果比勾形磁场更为显著。此外,还对重力条件下熔体内部热毛细-浮力对流的失稳机理进行分析,以研究磁场对临界Ma数的影响。 关键词:分离结晶;静态磁场;热毛细-浮力对流;数值模拟;CdZnTe (Edited by Xiang-qun LI) Foundation item: Project (51276203) supported by the National Natural Science Foundation of China Corresponding author: Lan PENG; Tel/Fax: +86-23-65112813; E-mail: penglan@cqu.edu.cn DOI: 10.1016/S1003-6326(15)63682-2 (9)
(9)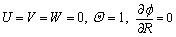 (10)
(10)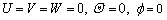 (11)
(11) , where H and S are the height of melt and the width of gap in non-dimensional form, respectively. In addition, the temperature difference in the radial direction is expressed in non-dimensionalized form as the Marangoni number, which is defined as
, where H and S are the height of melt and the width of gap in non-dimensional form, respectively. In addition, the temperature difference in the radial direction is expressed in non-dimensionalized form as the Marangoni number, which is defined as  .
.


静态磁场对分离结晶中熔体流动的影响

