文章编号: 1004-0609(2006)05-0887-07
大挤压比铝型材挤压过程的数值模拟
黄光法1, 林高用1, 2, 蒋 杰3, 王 芳3, 杨立斌1, 彭大暑1
(1. 中南大学 材料科学与工程学院, 长沙 410083;
2. 华中科技大学 塑性成形模拟及模具技术国家重点实验室, 武汉 430074;
3. 云南省机械研究设计院, 昆明 650031)
摘 要: 通过采用有限元法与有限体积法相结合, 并在有限体积法中进行分步计算的模拟方法, 在MSC Superforge有限元商业软件上成功实现了薄壁大挤压比铝型材挤压过程的数值模拟仿真, 获得壁厚t=1.0mm、 挤压比λ=98.27的卷闸门型材挤压过程的材料流动速度场、 应力场、 应变场、 温度场分布图, 数值模拟结果与理论分析结果吻合较好。 结果表明: 采用带导流槽的平模挤压大尺寸、 大挤压比型材, 可有效分配金属, 平衡金属流动速度。
关键词: 大挤压比; 铝型材; 有限元法; 有限体积法; 数值模拟 中图分类号: TG376.2
文献标识码: A
Numerical simulation of extrusion process of aluminum profile with large extrusion ratio
HUANG Guang-fa1, LIN Gao-yong1, 2, JIANG Jie3,
WANG Fang3, YANG Li-bin1, PENG Da-shu1
(1. School of Materials Science and Engineering, Central South University,Changsha 410083, China;
2. State Key Laboratory of Plastic Forming Simulation and Die Technology,
Huazhong University of Science and Technology, Wuhan 430074, China;
3. Yunnan Mechanical Research and Design Institute, Kunming 650031, China)
Abstract: A new simulation system was developed by integrating the finite element method (FEM) and the finite volume method (FVM) based on the theories of large deformation elastic-plastic finite element method and finite volume method. To avoid time-consuming and obtain reasonable results in the simulation, the optimized geometry models were employed in the pre-processor. The forming of a complex thin-walled aluminum profile with large extrusion ratio λ=98.27 and 1mm in thickness, was successfully simulated in the new simulation system on the platform of MSC Superforge. The simulation results are agreeable to the general extrusion principles. The distributions of velocity field, effective stress field, effective strain field and temperature field during the extrusion process were discussed and the metal process was analyzed in details. The results indicate that the flow guide is effective in balancing the metal deforming during the profile extrusion process with large extrusion ratio.
Key words: large extrusion ratio; aluminum profile; finite element method; finite volume method; numerical simulation
由于铝型材截面形状复杂, 一般都属于三维流动大变形问题, 挤压成形过程非常复杂。 因此, 挤压工艺和模具的设计与制作质量就成了挤压过程是否经济可行的关键之一。 数值模拟仿真是研究挤压变形过程的先进技术。 随着计算机硬件和软件技术的飞速发展, 基于有限元法与有限体积法的数值模拟在金属挤压成形中得到了广泛的应用。 Yang等[1]对曲线凹模三维非圆截面棒料稳态挤压过程进行了有限元分析。 韩国的Shin等[2]在1993年采用简化的三维有限元法获得了由圆形坯料挤压成方形、 正六边形、 "T"形截面的网格变形图。 Park等[3]采用刚塑性有限元法对非扭曲截面的三维螺旋稳态挤压过程进行了模拟, 获得了变形网格图和等效应变分布。 张新泉[4]采用简化的三维刚粘塑性有限元模拟了型材挤压过程的流动状态, 获得了典型截面上的等效应变、 流动速度分布和模具表面上的压力分布。 周飞等[5]采用三维刚粘塑性有限元方法, 对一典型的铝型材非等温成形过程进行了数值模拟, 给出了成形各阶段的应力、 应变和温度场分布情况。 于沪平等[6]采用塑性成型模拟软件DEFORM, 结合刚粘塑性有限元函数法对平面分流模的挤压变形过程进行了二维模拟, 得出了挤压过程中铝合金的应力、 应变、 温度以及流动速度等的分布和变化。 刘汉武等[7]利用ANSYS 软件对分流组合模挤压铝型材进行了有限元分析和计算, 找出了原模具设计中不易发现的结构缺陷。 闫洪等[8-11]利用ANSYS 软件作为平台, 对型材挤压过程进行了三维有限元模拟和分析, 获得了型材挤压过程的位移场、 应变场、 应力场, 提出了变形体内存在一个涡流场。 周飞等[12]还采用有限体积法对一复杂铝型材进行了数值模拟, 成功获得了挤压比为λ=38.19铝型材挤压模具载荷历史图以及挤压金属的应力、 应变、 温度以及流动速度等分布图。
然而, 对于铝型材产品特别是薄壁类(壁厚t〈1.8mm)大挤压比(λ>60)产品, 有限元法与有限体积法都存在着不足之处[13]: 前者在计算大变形问题中有限元网格会不断发生畸变, 需要不断进行网格重划分, 导致体积损失过大, 模拟精度显著降低, 且十分耗时; 后者在计算薄壁类大变形问题中要求Euler网格划分细致, 不能对变形体局部特征部位进行网格特别处理, 因此采用有限体积法模拟会占用大量计算机内存, 使得一般的计算机在计算规模和在计算时间上难以承受。 如果采用较粗的网格, 变形体特征部位又得不到准确的描述, 导致模拟结果精度得不到保证。 基于上述原因, 国内对于大变形挤压过程的数值模拟一直未能获得好的进展, 在DEFORM软件上很难实现挤压比大于40的模拟仿真。 针对这一情况, 本文作者在MSC Superforge有限元商业软件平台上, 采用有限单元与有限体积法相结合, 并采用分步算法: 在填充及导流模阶段采用有限元模拟方法, 而在材料流出导流模后采用了分步有限体积模拟方法, 成功地对一壁厚t=1.0mm、 最大尺寸为91.5mm、 挤压比λ=98.27的X5214卷闸门型材实现了数值模拟, 获得了该型材挤压过程中的材料流动速度、 应力、 应变、 温度分布图, 并对模拟结果进行了讨论。
1 基本理论
1.1 有限变形弹塑性有限元法理论
1) 虚功率方程(平衡方程)
变形体在塑性变形过程中, 每一个瞬间都要满足平衡关系, 也就是说要满足虚功原理。 根据虚功原理, 在外力作用下处于平衡状态的弹塑性体, 当发生位移约束容许的任意虚速度δVi时, 外力在虚速度上所做的功率等于弹塑性体内应力在虚应变速率上所做的功率。 因此, 按Langange描述的虚功率方程为[14]
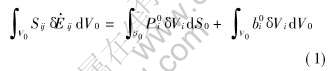
式中 Sij为第二Piola-Kirchhoff应力张量的分量, E[DD(-*2]·[DD)]ij为Green应变张量变化率的分量, P0i为与Pi相对应的在初始构形中的受截表面S0上的表面力分量, b0i为与bi相对应的在初始构形中的单位体积的体力分量, V0为与V相对应的物体在初始构形时的体积。
2) 本构方程
弹塑性体发生温度耦合的塑性变形时, 应力速率采用Cauchy应力的Jaumann导数 , 由VonMises屈服条件, 相关流动法则和加卸载准则导出本构方程为
, 由VonMises屈服条件, 相关流动法则和加卸载准则导出本构方程为
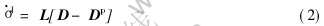
式中 为Cauchy应力的Jaumann导数; D为总的应变率张量; Dp为塑性应变率张量; L为弹塑性本构张量。
为Cauchy应力的Jaumann导数; D为总的应变率张量; Dp为塑性应变率张量; L为弹塑性本构张量。
3) 有限元列式
由于几何非线性和材料非线性, 需将平衡方程进行有限单元离散化, 最后可以得到整体有限元刚度方程:
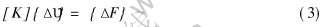
式中 [K]为总体刚度矩阵; {Δυ}为总体节点速度增量; {ΔF}为总体节点力增量。 式(3)通常用Newton-Raphson算法进行迭代求解。
1.2 塑性材料有限体积法基本理论
有限体积法采用空间固定的Eularian网格技术来描述材料相对于固定网格的流动, 突破了传统有限元技术模拟薄壁大变形材料流动的障碍, 回避了网格自动重新划分。 在挤压成形过程中材料的质量、 动量和能量也随之从一个单元流到另一个单元。 在材料流动的过程中, 必须满足以下控制方程[15-17]。
1) 质量守恒方程

2) 动量守恒方程
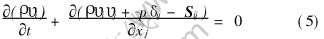
3) 能量守恒方程
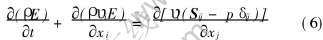
式中 ρ、 υi、 Sij、 p、 E分别为材料的密度、 速度矢量、 应力张量、 静水压力和内能。
4) 本构方程
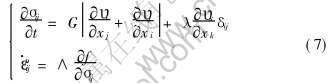
式中 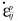 为塑性应变速率张量, ∧为与应力、 应变以及应变速率有关的系数, f为屈服函数。
为塑性应变速率张量, ∧为与应力、 应变以及应变速率有关的系数, f为屈服函数。
5) 状态方程
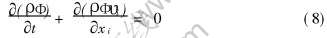
式中 Φ为任意状态变量, 如体积、 应力、 压力等。
6) 热平衡方程
根据热力学第一定律, 单元体内能量的变化率等于外力对单元体所做的功率和单元与外界进行热交换绿的总和。 因此, 材料单元的能量平衡方程为

式中 k为材料的导热系数, T为工件温度, cp为比热容。
采用基于Staggered Grid方法对上述控制方程进行有限体积展开, 然后采用龙格库塔法求解各微分方程, 从而得到有限体积内变形体的各种物理场量。
2 大挤压比薄壁型材数值模拟方法
本文作者经过深入研究, 通过简化和优化几何模型, 以及采用先进的有限元与有限体积法相互结合, 在有限体积模拟阶段进行分步计算的模拟方法, 实现大挤压比大尺寸薄壁卷闸门型材三维挤压过程的数值模拟。
2.1 几何模型简化与优化
目前, 大挤压比薄壁型材的数值模拟计算的主要限制因素是计算机的动态内存分配空间不足, 也就是说模拟这类型材挤压问题的单元网格规模太庞大。 如果能够在保证模拟精度不受太大影响的情况下对几何模型进行适当简化, 那么计算过程对内存容量要求就会降低。 因此本文作者对数值模拟的几何模型进行了以下优化。
1) 减小铸锭几何模型的高度H。 经作者反复数值模拟证明, 保证铸锭高度H大于压下量5mm以上, 对型材挤压的应变场、 速度场和温度场的分布和大小均无大的影响, 对应力场的分布没有影响, 但是对应力场的大小有一定影响, 比实际值偏低。 本文作者研究的铸锭几何模型高度选择为20mm, 模拟时压下量为8mm。
2) 在热挤压数值模拟过程中, 挤压筒内壁和模具预变形部分模面的摩擦属于粘着摩擦, 一般采用剪切摩擦模型, 而模具工作带部分属于滑动摩擦, 采用库仑摩擦模型比较理想。 所以, 在模具几何建模时, 采用分体式几何建模思想, 将挤压筒和模具预变形部分建成一个独立模型, 将模具工作带独立建成一个几何模型。 这样有利于在数值模拟时选择合适的摩擦模型, 达到提高模拟精度的目的。
2.2 有限元法与有限体积法相结合的分步模拟
由于该卷闸门型材不仅壁薄, 而且挤压比非常大, 如果从铸锭直接挤出产品会非常困难, 所以在该型材模具设计时先采用导流模进行预成形, 当金属充满预成形型腔后, 再流入成形模具的工作带。 这样可以明显降低局部挤压比, 有利于金属流动, 也有利于提高型材的质量, 但是对于数值模拟却更加困难了, 因为它增大了型腔的体积, 大大增加了数值模拟时单元网格数量。 为了该型材的数值模拟能够顺利进行, 本文作者采用有限元法与有限体积法结合, 在有限体积模拟阶段进一步分步的模拟方法, 以有效减少数值模拟的网格规模。
在型材填充导流模阶段, 局部挤压比小, 材料变形不会很剧烈, 用有限元法进行模拟所需的网格重划分次数较少, 因此非常适合采用有限元法进行数值模拟。 当金属开始进入工作带之后, 型材的壁厚小而导流槽的尺寸相对较大, 挤压比达30以上, 材料变形相当剧烈, 不适合采用有限元法进行数值模拟, 因此采用有限体积法进行数值模拟。 但是, 由于型材壁厚非常小, 需要将网格划分得很细, 如果在有限体积法数值模拟阶段进行一步模拟, 那么有限体积网格的规模会非常庞大, 往往会因为内存不足导致计算无法进行下去。 所以本文作者采用有限体积法模拟阶段进一步分步模拟方法, 将有限体积法模拟阶段再分为多个阶段进行模拟, 每一步的模拟结果作为下一步的初始条件。 这样, 在每一步中可以采用比较细致的网格, 而又不会占用很多的计算机资源。 通过上述处理, 本文作者在个人电脑上成功完成了该型材挤压过程的数值模拟。
具体做法如下。
1) 将用CAD软件建好的几何模型导入有限元法模拟系统中, 建立有限元网格体系, 然后进行其他具体的数值模拟参数设计, 进行第一阶段的有限元法数值模拟。 模拟完后, 将模拟结果输出到中间数据文件。
2) 将有限元法数值模拟后的中间数据文件导入到有限体积数值模拟系统中, 并实现各物理量的传递。 建立第一步有限体积法数值模拟的网格体系, 然后进行其他具体的数值模拟参数设计, 进行第二阶段的有限体积数值模拟的第一步模拟。 将第一步有限体积法模拟完的结果输出到中间数据文件。
3) 将2)中第一步有限体积法模拟完的中间数据文件导入到第二步的有限体积数值模拟系统中, 并实现各物理量的传递。 建立第二步有限体积法数值模拟的网格体系, 然后进行其他具体的数值模拟参数设计, 进行第二步有限体积数值模拟。 继续将模拟结果输出到中间数据文件。
4) 重复2)、 3)中的做法直到获得最终数值模拟结果。
3 卷闸门型材的挤压过程数值模拟
图1所示为一卷闸门型材横截面图, 其产品如图2所示。 该型材采用有导流模的平模挤压成形, 模具的工作带分布如图3所示, 模孔及导流孔平面示意图如图4所示。
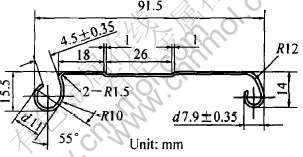
图1 型材截面示意图
Fig.1 Cross-section of X5214 profile

图2 型材工件图
Fig.2 Diagram of profile product
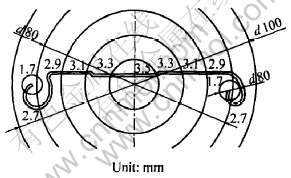
图3 模具工作带分布示意图
Fig.3 Different length of die land
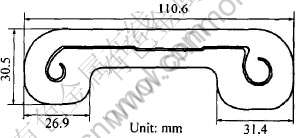
图4 模孔及导流模平面示意图
Fig.4 Positions of die orifice and flow guide
3.1 挤压参数
模拟挤压变形材料为6061铝合金, 其应力—应变关系如图5所示。 其他参数为: 铸锭成形温度500℃, 模具预热温度460℃, 挤压筒直径d120mm, 铸锭尺寸d114mm×20mm, 填充系数κ=1.05, 剪切摩擦因子μ=0.8, 滑动摩擦因数0.45, 挤压速度v=1mm/s, 挤压比λ=98.27。
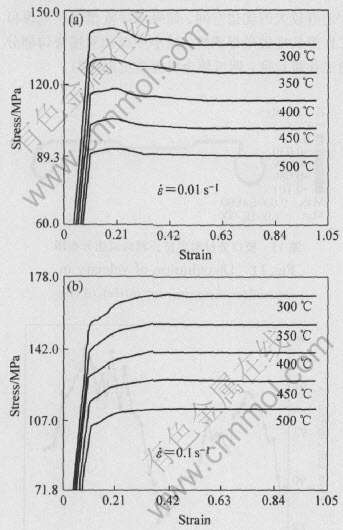
图5 6061铝合金压缩变形应力—应变曲线
Fig.5 Stress—strain curves of compressive deformation of 6061Al alloy
3.2 数值模拟结果及分析
基于上述数值模拟方法, 在电脑CPU为2200+、 内存为2GB的个人台式电脑上经过130多小时的计算, 获得了该卷闸门型材三维挤压过程的材料流动速度、 应力、 应变、 温度分布图。 图6~11所示为数值模拟截图。
图6所示为材料流动景象图。 由图可知材料越靠近模口处流动越复杂, 特别是形状突变处流动最复杂。 导流模的一个重要作用就是对材料流入模口前进行预分配, 使得材料流动趋向于均匀化。 根据图5的模拟结果, 模口处材料流动比较均匀, 表明本导流模的设计是合理的。 图7所示为挤压过程中材料变形的等效应力分布图。 从图中可以很清楚地看到, 挤出的型材应力分布基本均匀, 但应力值比较大, 在型材出模口处应力值最大, 最大值达46.5MPa。
图8和9所示分别为变形体在挤压成形过程中等效应变和温度场的分布和变化情况。 从图中可以看出, 温度场和等效应变场的分布情况非常相似, 表明在挤压过程中变形材料温度升高的能量主要来源于成形过程中的塑性变形能。 模口处的应变量和温度都是最高的, 更进一步说明了模具模口是材料流动最复杂, 变形最剧烈的部位。

图6 材料流动景象图
Fig.6 Distribution of material flow
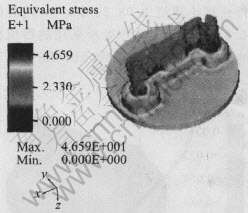
图7 等效应力分布图
Fig.7 Distribution of equivalent stress
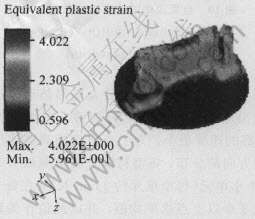
图8 等效应变分布图
Fig.8 Distribution of equivalent plastic strain

图9 温度分布图
Fig.9 Distribution of temperature stress
图10所示为变形材料沿挤压方向的流动速度分布图。 由图可知, 挤压进入稳定阶段后, 工件前端的流速为104.7mm/s, 而根据挤压速度和挤压比计算得到理论速度为98.27mm/s, 两者的相对误差为6.5%, 说明本文作者所采用的数值模拟方法模拟的结果与理论计算值吻合比较好。
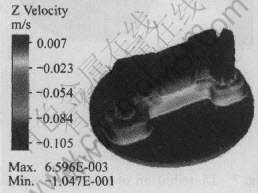
图10 金属流动沿挤压轴方向分布图
Fig.10 Distribution of velocity in extrusion direction
图11所示为模具出口处金属沿挤压方向的流动速度分布图。 从图中的云图看, 右端的速度偏大, 中部的速度最小。 为了更直观的观察速度沿型材长度方向的分布, 将型材沿长度方向展开并离散成58个小单元(每个单元约2mm长), 在每一个单元中取3个以上点求平均值, 并以此值作为该单元的轴向流速特征值。 将数据绘成折线图, 如图12所示, 其中, 横坐标为对应特征点的位置标号, 纵坐标为各单元的轴向流动速度。 从图12可以更清楚地看到型材截面各部分金属轴向流动速度的分布。 由于型材长度较长, 从整体上来说金属在模口处的速度分布比较均匀, 基本上达到生产要求, 但最大流速与最小流速仍然相差约7mm/s。 可见, 模具设计还有较大的优化空间。 如果对导流槽形状或模口工作带长度做局部调整, 减小中部和两端弯勾部分的工作带长度, 则可使金属流速更加均匀。

图11 模口处材料沿挤压轴向流速分布图
Fig.11 Distribution of velocity in extrusion direction on outlet of die
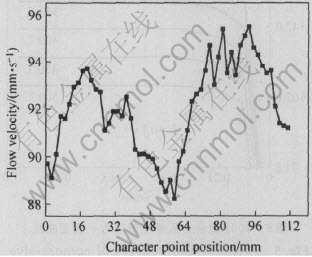
图12 模口处流速沿型材长度方向分布
Fig.12 Distribution of velocity in extrusion
direction for 56 parts of given cross-section
4 结论
1) 通过优化几何模型、 将有限元法与有限体积法相结合, 并在有限体积法模拟中采取分步计算, 成功实现了薄壁大挤压比型材挤压过程的三维数值模拟。
2) 采用上述复合的数值模拟方法, 获得了一壁厚t=1.0mm、 挤压比λ=98.27的卷闸门型材挤压过程的金属流动速度场、 应力场、 应变场、 温度场分布图。
3) 模拟分析数据表明, 采用有导流槽的平模挤压薄壁大挤压比型材可以有效分配金属, 平衡金属的流动速度。
致谢
对中南大学机电工程学院提供的MSC Superforge 有限元商业应用软件和湛利华老师的悉心指导表示感谢。
REFERENCES
[1]Yang D Y, Lee C M, Yoon J H. Finite element analysis of steady-state three-dimensional extrusion of section through curved dies[J]. Int J Mech Sci, 1989, 31(2): 145-156.
[2]Shin H W, Kim D W, Kim N K. A simplified three-dimensional finite-element analysis of the non-asymmetric extrusion processes[J]. Journal of Materials Processing Technology, 1993, 38: 567- 587.
[3]Park Y B, Yoon J H, Yang D Y, et al. Finite element analysis of steady-state three-dimensional helical extrusion of twisted sections using recurrent boundary condition[J]. Int J Mech Sci, 1994, 36(2): 137-148.
[4]张新泉. 铝型材挤压导流模设计的开发与数值分析[D]. 北京: 清华大学, 1988.
ZHANG Xin-quan. Exploitation and Numerical Analysis of the Flow Guide Design in Aluminum Alloy Profile Extrusion Process[D]. Beijing: Tsinghua University, 1988.
[5]周飞, 彭颖红, 阮雪榆. 铝型材挤压过程有限元数值模拟[J]. 中国有色金属学报, 1998, 8(4): 637-642.
ZHOU Fei, PENG Ying-hong, RUAN Xue-yu. Numerical simulation of aluminum material extrusion process by finite element method[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(4): 637-642.
[6]于沪平, 彭颖红, 阮雪榆. 平面分流焊合模成型过程的数值模拟[J]. 锻压技术, 1999, 24 (5): 9-111.
YU Hu-ping, PENG Ying-hong, RUAN Xue-yu. Simulation of the extrusion process using porthole dies[J]. Forging & Stamping Technology, 1999, 24(5): 9-111.
[7]刘汉武, 丁桦, 崔建忠. 铝型材挤压分流组合模有限元分析和计算[J]. 模具工业, 1999(4): 9-11.
LIU Han-wu, DING Hua, CUI Jian-zhong. FEM simulations and analysis of profile extrusion process in porthole die[J]. Die Industry, 1999(4): 9-11.
[8]闫洪, 包忠诩, 柳和生. 型材挤压过程三维弹塑性有限元模拟[J]. 轻合金加工技术, 2000, 28(11): 30-33.
YAN Hong, BAO Zhong-xu, LIU He-sheng. 3D-FE simulation of profile extrusion forming process[J]. Light Alloy Fabrication Technology, 2000, 28(11): 30-33.
[9]闫洪, 包忠诩, 柳和生, 等. 基于数值模拟的铝型材挤压变形规律的研究(Ⅰ)[J]. 锻压机械, 2000, 5: 29-30.
YAN Hong, BAO Zhong-xu, LIU He-sheng, et al. Study of profile extrusion deformation law based on numerical simulation(Ⅰ)[J]. Metal-forming Machinery, 2000, 5: 29-30.
[10]闫洪, 包忠诩, 柳和生, 等. 基于数值模拟的铝型材挤压变形规律的研究(Ⅱ)[J]. 锻压机械, 2000, 6: 31-32.
YAN Hong, BAO Zhong-xu, LIU He-sheng, et al. Study of profile extrusion deformation law based on numerical simulation (Ⅱ)[J]. Metal-forming Machinery, 2000, 6: 31-32.
[11]闫洪, 包忠诩, 柳和生, 等.角铝型材挤压过程的数值模拟[J]. 中国有色金属学报, 2001, 11(2): 202-205.
YAN Hong, BAO Zhong-xu, LIU He-sheng, et al. Numerical simulation of angle aluminum profile extrusion processes[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(2): 202-205.
[12]周飞, 苏丹, 彭颖红, 等. 有限体积法模拟铝型材挤压成形过程[J]. 中国有色金属学报, 2003, 13(11): 65-70.
ZHOU Fei, SU Dan, PENG Ying-hong, et al. Simulation of aluminum material extrusion process with finite volume method[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(11): 65-70.
[13]罗超, 李大勇, 尹纪龙, 等. 薄壁类铝型材挤压成形的一种有效模拟方法[J]. 上海交通大学学报, 2004, 38(7): 1134-1137.
LUO Chao, LI Da-yong, YIN Ji-long, et al. An effective simulation method for aluminum profile extrusion process[J]. Journal of Shanghai Jiaotong University, 2004, 38(7): 1134-1137.
[14]Bathe K J. Finite Element Procedures in Engineering Analysis[M]. Englewood Cliffs: Prentice-Hall, 1982.
[15]Fletcher C A J. Computational techniques for fluid dynamic[J]. Berlin: Springer-Verlag, 1991, 1: 15-132.
[16]Versteeg H K, Malalasekera W. An Introduction to Computational Fluid Dynamics The Finite Volume Method[M]. England: Longman Group Ltd, 1995.
[17]de Vries E, Ding P. Simulation of 3D forging and extrusion problems using a finite volume method[A]. Proceeding of 17th MSC JAPAN Users Conference[C]. Japan: MSC Software Company, 1999. 155-161.
基金项目: 云南省省院省校科技合作计划资助项目(2003UABAB05A050); 华中科技大学塑性成形模拟及模具技术国家重点实验室开放基金资助项目(04—06)
收稿日期: 2005-08-09; 修订日期: 2005-12-02
通讯作者: 林高用, 副教授, 博士; 电话: 0731-8836485; E-mail: gylin6609@ yahoo.com.cn
(编辑何学锋)