龙背湾低导流洞进口边坡变形稳定分析及加固处理

李毅^{1, 2}，陈益峰^{1, 2}，周嵩^{1, 2}，周创兵^{1, 2}

(1. 武汉大学 水资源与水电工程国家重点实验室，湖北 武汉，430072；

2. 武汉大学 水工岩石力学教育部重点实验室，湖北 武汉，430072)

摘要：利用勘测的龙背湾水电站低导流洞进口边坡表层岩体参数，分析自然边坡的安全状态，修正边坡表层岩体的强度参数，并进行初始应力场计算。采用多节理本构模型，对边坡开挖时出现的卸荷裂缝处的岩体进行模拟，并分析裂缝的成因。对初步的加固措施进行模拟，分析开挖过程中，边坡的变形、稳定情况，并在此基础上，对原加固方案进行修改和补充，结合边坡的水位骤降工况，分析边坡的变形稳定情况。研究结果表明：加固措施具有可行性和有效性，为边坡的开挖、加固提供了理论依据。

关键词：边坡；参数修正；多节理；加固；水位骤降

中图分类号：TU641          文献标志码：A         文章编号：1672-7207(2013)07-2958-07

Analysis of deformation stability on Longbeiwan low diversion tunnel entrance slope and reinforcement

LI Yi^{1, 2}, CHEN Yifeng^{1, 2}, ZHOU Song^{1, 2}, ZHOU Chuangbing^{1, 2}

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;

2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering,

Ministry of Education, Wuhan University, Wuhan 430072, China)

Abstract: Using the investigated rock parameters of Longbeiwan low diversion tunnel entrance slope, the status quo of the slope was analyzed. The rock strength parameters of the slope surface were modified and the initial stress field was calculated. Multi-joint model was used to simulate the unloading cracks during the excavation, and the causes were analyzed. The original reinforcement measures were simulated, and then, the deformation and stability situation during the excavation were analyzed. On the basis of these, reinforcement measures were modified and enhanced, and deformation and stability were analyzed when the slope is being suffered by a rapid drawdown of water level. The results show that the reinforcement measures are feasible and effective, which can provide theoretical support to the excavation and reinforcement of the slope.

Key words: slope; parameter correction; multi-joint; reinforcement; rapid drawdown of water level

工程边坡的安全稳定评价一直都是岩土工程领域研究的重点和难点之一，其岩土参数的不确定性^[1-3]、地质条件的复杂性^[4]及所处工况的多样性^[5-7]都是研究的热点。对于岩土体参数的反分析方面，李宁等^[8]提出：参数分析所得结果须满足边坡现状；许宝田等^[9]对层状岩体的边坡稳定及其支护措施进行了研究；沈金瑞等^[10]运用FLAC^3D对多组节理且较发育的岩体边坡进行了稳定性安全评价；朱泽奇等^[11]运用FLAC^3D进行了层状岩体变形与强度各向异性特性的研究。水位骤降对边坡影响方面的研究成果也较多^[12]。龙背湾低导流洞进口边坡属于典型多组节理岩体，其参数的不确定性、地质的复杂性、工况多样性都具代表性。通过对工程的初步勘探发现：该地区岩石软弱，风化层比较深，岩石强度低，导流洞进口高边坡开挖后，形成了坡度较陡的裸露边坡，边坡表层由风化严重的页岩和砂岩相互胶合而成，其强度参数准确性不足，需要进行调整。开挖过程中，低导流洞进口EL422.7 m马道以上边坡开挖后出现了卸荷裂缝，裂缝的出现必然会对工程进度造成影响，急需采取措施，防止边坡开挖过程中出现安全事故。在水库蓄水以后地下水位将大幅抬高，导流过程中，水位下降速度快，渗流对边坡的影响显著，因此需要全面考虑该边坡的稳定问题，采取更加有效的措施，抑制边坡进一步恶化，保证施工及蓄水期边坡的安全。

1  工程地质条件

导流洞进口边坡地质状况极其复杂，导流洞洞脸地层岩性为志留系龙马溪群的S₁ln²薄-中厚层砂岩夹页岩，砂岩厚度约占总厚度的60%。岩层产状褶皱影响产状变化较大，在洞轴线(褶皱)的西侧岩层产状为0°∠65°，东侧产状为202°∠81°，岩层总体产状为0°∠65～70°。褶皱轴面的发育方向与岩层走向基本一致。裂隙的发育主要方向主要为走向NEE，倾NNW，倾角63°~83°裂隙延伸不长，相对硬质砂岩中裂隙较发育，软岩页岩中裂隙不发育，裂隙内主要以泥质充填为主。岩体中线裂隙率为3%，岩体的完整性差。设计方提供的结构面建议参数如下：III类岩体中结构面内摩擦角Φ=26°，黏结力C=0.1 MPa；IV类岩体中结构面内摩擦角Φ=15°，黏结力C=0.06 MPa；V类岩体中结构面内摩擦角Φ=12°，黏结力C=0.03 MPa。图1所示为边坡的开挖和支护的示意图，岩体的主要参数见表1。

2  初始应力场计算及参数校正

边坡计算网格见图2，网格总单元数3 395，总节点数6 920。模型左边边界取至河道中央，右边边界取至边坡坡顶，底部向下取至坡高等长高度。边界约束条件为：垂直方向和底部均采用链杆约束。坐标系X轴指向山坡方向，垂直向上为Z轴。

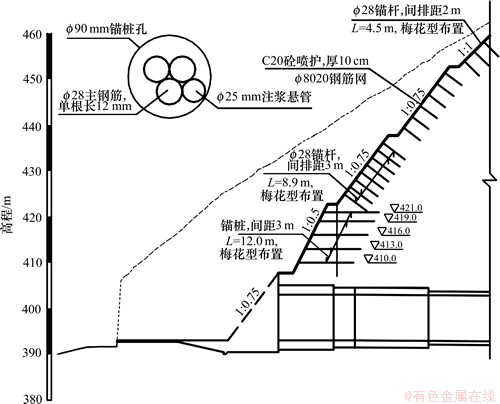
图1  开挖边坡支护示意图

Fig.1  Excavation and reinforcement of slope

表1  岩石参数

Table 1  Rock parameters

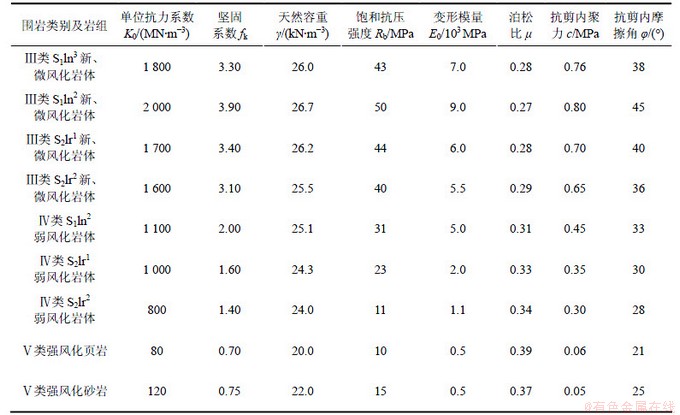
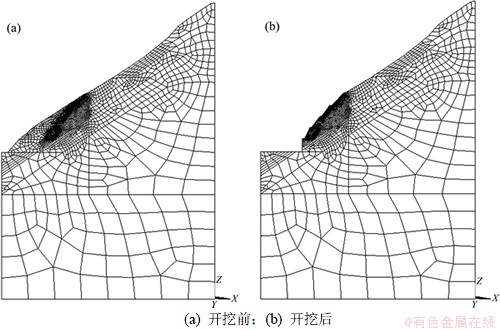
图2  边坡开挖前、后有限元网格

Fig.2  Mesh of slope before and after excavation

首先，利用稳定渗流的有限元程序，计算出边坡的初始渗流场。渗流场压力水头分布如图3所示。在考虑初始地下水渗流场的基础上，计算边坡初始地应力场，初始地应力场按自重应力场计算。从计算结果来看，计算不能收敛，破坏不仅有沿强、弱风化带的滑动破坏，而且还有沿层状结构面的剪切、拉伸破坏。同时，采用毕肖普法、简布法和Gle/morgenstern-price等刚体极限平衡法，分别按强风化页岩和强风化砂岩强度计算自然边坡的抗滑稳定性，边坡的抗滑稳定安全系数约等于1.0，滑动面主要沿岩体强、弱风化带交界面展布。对比基于有限差分的降强度法及刚体极限平衡法计算结果，从破坏面位置情况来看，滑动破坏面基本一致，但基于有限差分的降强度法模拟了层状结构面的作用，其破坏屈服区还包含结构面中的破坏屈服，因此，尽管刚体极限法计算的安全系数约为1.0，但基于有限差分的降强度法计算安全系数小于1.0，计算是发散的。

根据有限差分法计算结果，岩块屈服破坏主要发生在强风化区内，而结构面屈服破坏发生在强风化及弱风化区域内，显然结构面的存在，对自然山坡的稳定性有不可忽略的影响。考虑到自然山坡没有滑移，其抗滑稳定安全系数至少大于1.0，因此，有必要对岩体的力学参数作一些微调。参数调整原则：

(1) 天然边坡处于稳定状态，边坡经受过降雨等因素影响仍然处于稳定状态，其抗滑稳定安全系数应大于1，并有一定的强度储备。

(2) 边坡开挖到某一高程时，仍处于安全状态，其安全系数亦大于1。

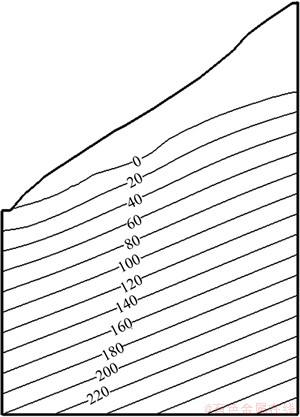
图3  初始渗流场压力水头等值线图(单位：m)

Fig.3  Initial seepage pressure head of slope

具体的参数调整，需要通过大量的试算，并根据目前开挖破坏情况确定。目前的破坏情况是边坡开挖以后，发生了结构面拉裂，但边坡并没有滑动破坏。但也有可能岩体具有一定的流变特性，开挖以后，地应力释放荷载可能不是一下子释放出来，而是有一个时间过程。这个过程有多长，没有确切的流变试验结果。从安全考虑，按开挖后岩体单独承担75%地应力释放荷载时处于临界稳定状态，估计岩体的强度参数。

试算确定的参数如下：强风化岩块的凝聚力为0.075 MPa，摩擦角为25°；结构面的凝聚力为0.035 MPa，摩擦角为14°，抗拉强度默认为0 MPa。

3  裂缝处理的措施

低导洞进口洞脸407.7~422.7 m高程地层岩性为志留系龙马溪群的S1ln2薄-中厚层砂岩夹页岩，岩层产状褶皱影响产状变化较大，在洞轴线(褶皱)的西侧岩层产状为0°∠65°，东侧产状为202°∠81°，褶皱轴面的发育方向与岩层走向基本一致。裂隙的发育主要方向为NEE向，裂隙延伸不长，相对硬质砂岩中裂隙发育，软岩页岩裂隙不发育，裂隙内以泥质充填为主。在裂隙发育的范围内岩体主要为强风化，岩体完整性差。

从现场发育的裂隙走向、裂面特征来看，裂缝成因为边坡形成后暴露时间过长，边坡处应力重新分布，导致产生卸荷后的边坡松弛拉裂。拉裂走向是追踪岩层已有的裂面和层面等相对弱面发育。现场裂缝的表面有泥质物，说明现在形成的裂缝面是在原裂面上发育的。从类似工程的卸荷裂缝的发育统计及室内光弹模型试验成果推测：裂缝开展深度在坡度75°时为边坡高度的一半，深度在8 m以内，边坡后缘展开宽度为1/3~1/5，推测宽度3~5 m。

4  边坡开挖变形稳定计算

根据上述措施，对边坡进行开挖变形稳定计算，开挖计算按2个分级进行，即：开挖坡顶~408 m， 408~393 m。

4.1 坡顶至408 m高程

根据实际的施工情况，在第1分级边坡开挖计算行过程中，首先进行开挖但不加固的计算。

在前述初始地应力计算的基础上，将所有的地应力开挖释放荷载一次施加，计算最终不能收敛。究其原因，主要是结构面的错动和张开变形破坏，导致强、弱风化区的岩块应力改变，边坡最终破坏，计算发散。

若假设岩体的应力释放有一个时间过程，则在不同时间具有不同的应力释放量。需要通过黏弹塑性计算才能完全模拟应力释放随时间的变化过程，而这要求大量的岩体蠕变试验，得到有关参数才能进行。在没有这些参数的情况下，通过应力释放率来分析。边坡开挖的一瞬间，边坡将释放所有的弹性和塑性变形，而黏性变形则是慢慢释放，如果加固比较早，能限制更多黏性变形的发展。例如在岩体加固前，岩体释放了75%的地应力释放荷载，而剩下的25%则由岩体与加固措施共同承担。地应力释放荷载的比例中隐含了时间因素，若这个比例高，则表示加固措施施加晚，若这个比例低，则表示加固措施施加早。

按75%的地应力释放荷载由岩体单独承担，岩体不考虑加固措施，计算结果表明，尽管岩体没有整体滑动破坏，但在结构面中产生了错动屈服和张拉破坏。图4所示为边坡的张拉屈服区分布位置，其中，tension-n和tension-p分别表示正在发生和已经发生张拉破坏的塑性屈服区。从图4可见，在423 m高程台阶处及其附近的区域岩体结构面发生了张拉屈服。和现场实际的开裂位置对比，发生的区域基本一致，差别在于实际的开裂集中在某个位置，而计算的结果是分布在某个区域。造成这种差异的原因，一方面实际岩体是非均匀的，而计算中每一类材料按均匀处理；另一方面，实际的岩体中，边坡下部位置有可能确实存在少量的张拉屈服，只不过在实际的开裂区域，张开量特别大，完全显示了出来，而其他位置由于比较小，不容易发现。

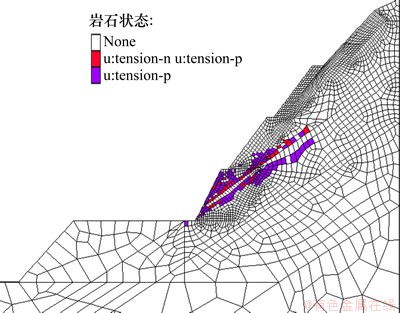
图4  边坡开挖坡顶至-408 m高程拉伸破坏图

Fig.4  Tensile failure of slope excavation from top to 408 m

根据设计院提供的加固措施：407.7~459 m高程间的开挖坡面施加喷锚支护，喷混凝土厚度10 cm，锚杆直径28 mm，深度为从上往下上部第2台阶以上边坡为4.5 m；上部第2和第3台阶之间为8 m，间排距为第2台阶以上为2 m；上部第2和第3台阶之间为3 m。第3台阶以下开挖坡面布置锚筋桩，由3根直径为28 mm的钢筋捆扎外围包裹直接为0.09 m的混凝土构成，长度12 m，间排距2 m和3 m。其中钢筋按Ⅱ级钢筋考虑，抗拉强度为310 MPa，钢筋按MISES屈服准则模拟其屈服。

施加剩余的25%的地应力释放荷载，由加固措施和岩体共同承担，计算能够收敛。图5和图6所示分别为开挖及加固后合位移增量等值线图、屈服区云图。边坡开挖后，由于强风化层变形模量低，加上结构面的影响，边坡表面出现微量拉应力。从图5可以看到，变形基本集中在强风化层内，最大合位移增量为 0.108 m，位于开挖坡面的上部。从图6可以看到，在边坡开挖以后，在强风化与弱风化交界区域岩块发生屈服。可见：施加了锚筋桩和喷锚支护后，开挖到408 m高程时，边坡基本能够稳定。

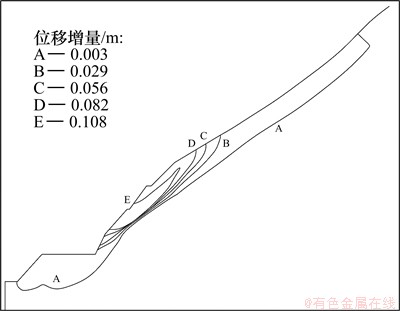
图5  开挖到408 m时的位移增量等值线分布

Fig.5  Displacement increment of slope excavated from top to 408 m

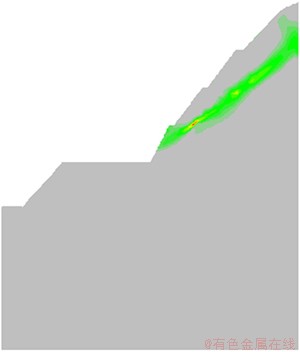
图6  开挖到408 m时的屈服云图

Fig.6  Yield of slope excavation from top to 408 m

4.2  408~393 m高程

在上述开挖加固计算的基础上，进行直立部分的开挖计算。首先，在直立部分开挖计算过程中，不施加加固措施，地应力释放荷载由岩体独立承担，即承担100%的地应力释放荷载。从计算结果来看，计算不能收敛，表示岩体必须通过加固措施才能维持稳定。图7所示为开挖后的屈服区，从图7可以看到，边坡发生塑性区贯通，岩体不能维持稳定，因此，需要加固。

加固措施采用锚杆，直径36 mm，长度20 m，间距0.5 m。加固前后的应力释放荷载比例需要通过试算才能确定。分别按90%，80%，70%，60%和50%的比例由岩体独自承担进行试算。从计算结果可知，只有在荷载比例为50%时，边坡才能稳定，说明了下部边坡岩体在开挖以后的自稳能力较低，如果不加以及时加固处理，岩体将在开挖以后垮塌。

锚杆施加过程中，对锚杆周围的岩体进行了灌浆处理，提高了周围岩体的整体性，假如固结灌浆后，弱风化区域的结构面内凝聚力增加为0.1 MPa，抗拉强度提高为0.05 MPa，而内摩擦角不变。在考虑加固措施的基础上，施加剩余的50%地应力释放荷载进行计算，计算能够收敛。图7和图8所示分别为开挖加固后的屈服区云图、位移增量等值线图。

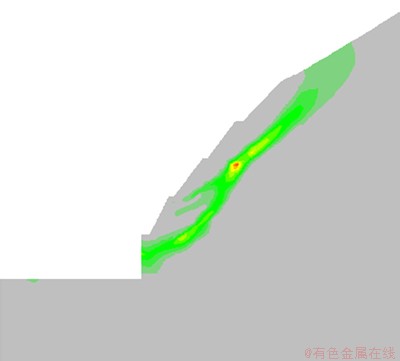
图7  开挖408~393 m时的屈服云图

Fig.7  Yield of slope for excavation from 408 to 393 m

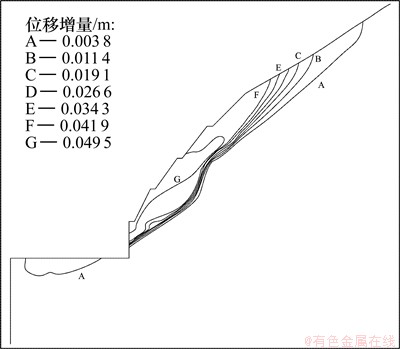
图8  开挖408~393 m时的位移增量

Fig.8  Displacement increment for excavation from 408 to 393 m

边坡开挖后产生回弹变形，边坡中应力调整很大，在坡面产生小拉应力区。从图8可以看到，坡面最大合位移增量约49.5 mm，位于开挖坡面上部，说明下部边坡开挖，对上部边坡具有影响；从图7可以看到，在直立边坡开挖并加固以后，上部边坡岩体屈服区没有扩大。

因此，直立坡的开挖，对开挖区边坡的稳定影响大，不施加灌浆、支护措施时，该部分将失去稳定，垮塌后将影响上部岩体的稳定。

5  水库水位骤降工况下边坡的变形稳定计算

水库水位骤降模拟中假设施工期围堰遭遇20年一遇洪水，上游水位从442.87 m降至398.00 m，历时48 h。首先进行水库水位骤降过程计算，水库水位骤降后边坡中瞬时压力水头等值线分布见图9。

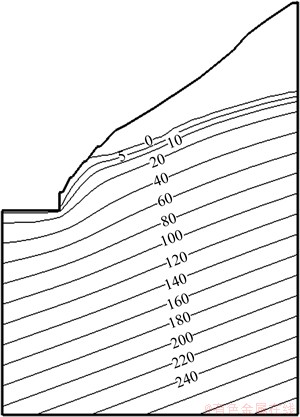
图9  水位骤降边坡渗流场压力水头等值线分布 (单位：m)

Fig.9  Seepage pressure head of slope after rapid drawdown of water level

在渗流场计算基础上，进一步进行边坡的变形稳定计算。水位骤降使边坡中的应力调整在节理密集区比较复杂，边坡表层存在拉应力区；水位骤降边坡位移增量图如图10所示。从图10可以看到，在水位骤降情况下，边坡最大位移增量为40.7 mm，位于渗流逸出位置附近；在水位骤降情况下，屈服区变化不大，主要集中在渗流溢出位置，发生开裂的台阶附近。从计算的结果看，采用支护措施后，在水位骤降条件下，安全储备不高。

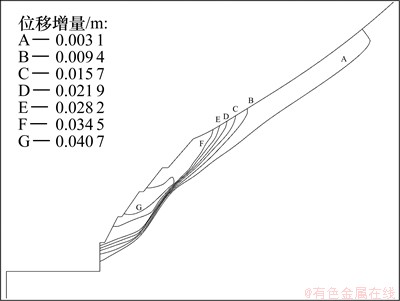
图10  水位骤降边坡位移增量

Fig.10  Displacement increment of slope after rapid drawdown of water level

6  结论

(1) 按提供的强度参数计算，在天然情况下处于临界状态，在开挖后是不稳定的，而实际边坡没有滑动破坏，但发生开裂。

(2) 在423 m高程台阶处及其下坡面都有可能开裂，这和实际情况基本相符，但不是完全相符。其原因与岩体的处理有关，计算中同一风化状态的岩体按均匀考虑，而岩体实际是非均匀的。

(3) 考虑锚杆及锚筋桩加固处理，目前开挖的边坡能够满足稳定要求。由于直立部分岩体对上部边坡的变形影响较大，因此必须对其进行加固。

(4) 水位骤降对边坡的稳定影响很大，即使在开挖完成后边坡能维持稳定，但在考虑水位骤降情况下，边坡也有可能不能稳定。在提高结构面强度及施加锚杆的情况下，边坡安全储备不高。

参考文献：

[1] Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36: 612-624.

[2] Phoon K K, Kulhawy F H. Evaluation of geotechnical property variability[J]. Canadian Geotechnical Journal, 1999, 36: 625-639.

[3] 张征, 刘淑春, 鞠硕华. 岩土参数空间变异性分析原理与最优估计模型[J]. 岩土工程学报, 1996, 18(4): 40-47.

ZHANG Zheng, LIU Shuchun, JU Shuohua. The optimum estimation model and the principle of spatial variability analysis of rock and soil parameters[J]. Chinese Journal of geotechnical Engineering, 1996, 18(4): 40-47.

[4] 周创兵, 陈益峰, 姜清辉, 等. 论岩体多场广义耦合及其工程应用[J]. 岩石力学与下程学报, 2008, 27(7): 1329-1340.

ZHOU Chuangbing, CHEN Yifeng, JIANG Qinghui, et al. On generalized multi-field coupling for fractured rock masses and its applications to rock engineering[J]. Chinese Journal of Hydraulic Engineering, 2008, 27(7): 1329-1340.

[5] Fox D M, Bryan R B, Price A B. The influence of slope angle on final infiltration rate for interrill condition[J]. Geoderma, 1997, 80: 181-194.

[6] Berilgen M M. Investigation of stability of slopes under drawdown conditions[J]. Computers and Geotechnics, 2007, 34: 81-91.

[7] 刘杰, 李建林, 张玉灯, 等. 基于拟静力法的大岗山坝肩边坡地震工况稳定性分析[J]. 岩石力学与工程学报, 2009, 28(8): 1562-1570.

LIU Jie, LI Jianlin, ZHANG Yudeng, et al. Stability analysis of dagangshan dam abutment slope earthquake based on pseudo-static method[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1562-1570.

[8] 李宁, 尹森菁. 边坡安全监测的仿真反分析[J]. 岩石力学与下程学报, 1996, 15(1): 9-18.

LI Ning, YIN Senqing. Back analysis of the safety factor for slope[J]. Chinese Journal of Hydraulic Engineering, 1996, 15(1): 9-18.

[9] 许宝田, 钱七虎, 阎长虹, 等. 多层软弱夹层边坡岩体稳定性及加固分析[J]. 岩石力学与工程学报, 2009, 28(s2): 3959-3964.

XU Baotian, QIAN Qihu, YAN Changhong, et al. Stability and strengthening analysis of slope rock mass containing multi-weak interlayers[J]. Chinese Journal of Rock Mechanics and Engineering, 2009s, 28(s2): 3959-3964.

[10] 沈金瑞, 林杭. 多组节理边坡稳定性FLAC^3D数值分析[J]. 中国安全科学学报, 2007, 17(1): 29-33.

SHEN Jinrui, LIN Hang. The numerical analysis on the stability of slope with several sets of joints by FLAC^3D[J]. China Safety Science Journal, 2007, 17(1): 29-33.

[11] 朱泽奇, 盛谦, 梅松华, 等. 改进的遍布节理模型及其在层状岩体地下工程中的应用[J]. 岩土力学, 2009, 30(10): 3115-3122.

ZHU Zeqi, SHENG Qian, MEI Songhua, et al. Improved ubiquitous-joint model and its application to underground engineering in layered rock masses[J]. Rock and Soil Mechanics, 2009, 30(10): 3115-3122.

[12] 贾官伟, 詹良通, 陈云敏. 水位骤降对边坡稳定性影响的模型试验研究[J]. 岩石力学与工程学报, 2009, 28(9): 1798-1803.

JIA Guanwei, ZHAN Liangtong, CHEN Yunmin. Model test study of slope instability induced by rapid drawdown of water level[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1798-1803.

(编辑  赵俊)

收稿日期：2012-08-04；修回日期：2012-10-20

基金项目：国家自然科学基金资助项目(51079107，51179136)；国家优秀青年科学基金项目(51222903)

通信作者：陈益峰(1974-)，男，福建漳平人，教授，从事岩土多场耦合、渗流及边坡稳定性分析研究；电话：027-68774295；E-mail: csyfchen@whu.edu.cn