文章编号：1004-0609(2014)10-2582-06
混合物料中石墨组分的碎裂特性及参数估计
田金星1, 2，谭旭升1, 2
(1. 武汉理工大学 资源与环境工程学院，武汉 430070；
2. 武汉理工大学 矿物资源加工与环境湖北省重点实验室，武汉 430070)
摘 要：利用Reid总体平衡微积分分批磨碎动力学方程，研究石墨-方解石物料混合磨碎时，石墨的磨碎动力学行为。结果表明：对碎裂速率函数Si而言，混合磨碎时石墨组分的碎裂速率函数Si表现为与时间t相关，即ln mi与t的关系曲线呈非线性关系。同时，模型仿真结果表明，石墨组分表现的非线性碎裂结果的模拟值与实验值吻合度较高；而石墨组分混合磨碎的碎裂分布函数bij则与单独磨碎时的碎裂分布函数bij基本相同。该结论可作为石墨磨碎生产实践的理论指导。
关键词：石墨；混合物料；磨碎；碎裂参数
中图分类号：TQ170.1 文献标志码：A
Fracturing characteristic and parameter estimate of graphite component of mixture
TIAN Jin-xing1, 2, TAN Xu-sheng1, 2
(1. College of Resources and Environmental Engineering, Wuhan University of Technology, Wuhan 430070, China;
2. Hubei Key Laboratory of Mineral Resources Processing and Environment, Wuhan University of Technology, Wuhan 430070, China)
Abstract: The batch grinding kinetic equation based on Reid balance calculus was used to study the grinding dynamics behavior of graphite in a mixed material of graphite-calcite. The results show that, for the function on the broken rate Si, the fracture rate of graphite components in function expression is related to time t, which shows the nonlinear relationship between ln mi and t. The simulation values and experiment values of graphite component nonlinear fracture results are well agree with each other. For the fracture distribution function bij, the fracture distribution functions of graphite components in the mixed material grinding and separate mineral grinding are basically the same. The aforementioned conclusion can take theoretical guide for the production practice of graphite grinding.
Key words: graphite; mixed material; grinding; fracturing rate function
天然石墨由于其优异的导电、导热、耐高温、自润滑和化学稳定等特性，以及它在石油、化工、电子、冶金、环保、航空、航天及核能等领域的广泛应用[1-2]，使得它成为当今世界高新技术产品不可或缺的重要材料[3-4]和战略性新兴材料[5]。用天然石墨制备的球型石墨具有高的首次充放电库伦效率和高的大电池体积比容量[6]，在锂离子电池、燃料电池等高能电池的电极材料领域有着广阔的应用前景[7]。因此，石墨独特的性能以及特殊的生成条件使其成为一种宝贵且不可再生的资源。
然而，将蕴藏于矿物中的天然石墨加工成电极材料 ，则必需对其进行选矿、提纯[8]、粉碎、整形、包覆等加工[9]才能实现。实际上，天然石墨作为原料的经济价值是：鳞片越大(尺寸大于0.147 mm)和鳞片越小(0.005~0.030 mm)的石墨，其经济价值越高。因此，为使石墨资源的应用价值最大化，首先必须使矿物中的大鳞片石墨在选矿过程中尽可能多地得到保护而不被破坏[10-11]。因此，就必须研究石墨组分在混合磨碎环境下的碎裂参数特性，进而为石墨选矿的最佳磨碎作业参数确定提供理论指导；其次，还必须将经选矿而得出的中间粒级的石墨进行深加工，即再经超细粉碎、提纯、包覆等作业而最终制得电极材料的原料—球形石墨，从而提高其利用价值。但此时对超细粉碎作业的要求与选矿的磨碎作业相反，主要是如何使石墨鳞片尽快的碎裂，以便降低其超细粉碎作业的能耗和提高粉碎效率，为此，就必须研究石墨单独磨碎时的碎裂参数特性，从而为超细粉碎作业的参数选择提供理论依据。
迄今为止，对天然石墨碎裂参数特性进行系统理论研究的文献较为少见。本文作者利用Reid[12]总体平衡微积分分批磨碎动力学方程，研究石墨单独磨碎和石墨-方解石物料混合磨碎时，石墨的碎裂参数(碎裂速率函数Si和碎裂分布函数bij)特性，并通过积分变换建立了石墨混合磨碎的非线性碎裂速率函数Si的准线性模型。
1 实验
1.1 实验条件
采用XMB-70型三辊四筒磨矿机分批进行石墨、石墨-方解石混合物料的磨碎实验。所用磨筒容积为2 L，磨筒转速定为200 r/min，磨碎介质为球并以体积充填率为基准，即物料体积与球隙体积之比为1:1。由于影响物料碎裂的因素很多[13]，为了使实验过程尽可能简便且又不影响对物料碎裂规律的研究，在实验过程中保持磨筒转速、钢球充填率均不变。
1.2 物料的粒度测定
物料的粒度测定选用XSB-70型振筛机，物料的筛分时间取30 min，但在制取石墨单粒级物料时，筛分时间取1 h。
对于石墨-方解石混合物料，采用酸溶法测定石墨各粒级的质量，并利用物料平衡原理计算方解石各粒级的质量。
2 结果与讨论
2.1 理论依据
Reid总体平衡微积分分批磨碎动力学方程的表达式如下：
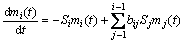(1)
式中：mi(t)为t时刻第i粒级的质量分数；Si为碎裂速率函数，表示第i粒级物料单位时间内被碎裂的分数；bij为碎裂分布函数，表示第j粒级物料经初次粉碎后进入第i粒级的分数；对于第一粒级(最粗粒级)，有
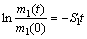(2)
关于式(1)中参数Si、bij的特性及其测定方法，已有许多学者作过详细的研究[14-15]，本实验中采用预 估-反算法估计碎裂参数。
2.2 碎裂速率函数Si
图1和2所示分别为石墨在单独磨碎和石墨-方解石物料混合磨碎时，石墨的磨碎动力学曲线。
由图1可以看出，石墨在单独磨碎时，其磨碎动力学曲线为一直线，这表明同一粒级中石墨的碎裂速率函数Si并不随时间的变化而改变；对于不同的粒级，石墨的碎裂速率函数Si随粒级的增大而增大。文献[16]对这一现象产生的原因进行了分析。
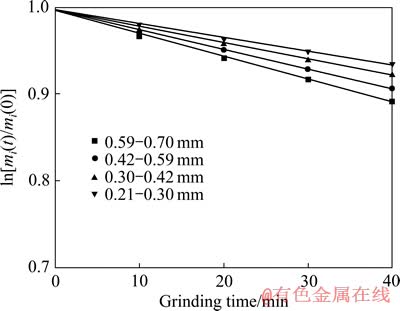
图1 石墨单独磨碎时的动力学曲线
Fig. 1 Grinding kinetic curves of graphite
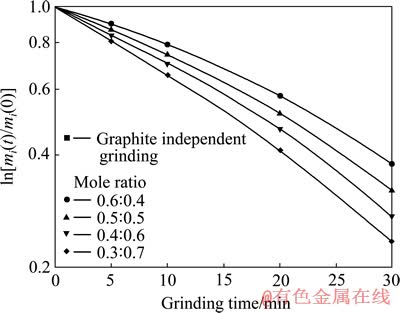
图2 混合物料石墨组分的磨碎动力学曲线
Fig. 2 Kinetic curves of graphite component of mixture
由图2可知，石墨在混合磨碎时，石墨组分的磨碎动力学行为是非线性的，即表现为碎裂速率函数Si与时间t有关；与单独磨碎时相比，混合磨碎时石墨组分的碎裂速率函数Si有所增大。
对石墨单独磨碎时的动力学曲线进行的研究[16]表明，石墨在一定的磨碎时间内，具有显著的细粒级零阶产出特征，即
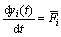(3)
式中：yi(t)为t时刻小于i粒级的累积产率；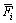
为小于粒度xi的细粒级零阶产出常数。且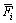和xi间满足下列关系式：
(4)
式中：k和γ均为常数。
再假设
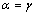(5)
即可采用预估-反算法以及磨碎数学模型对上述假设进行仿真检验。
图3所示为在上述假设成立的前提下，得到的模型仿真结果和实验结果。
从图3可以看出，石墨磨碎的模型仿真结果和实验结果吻合度较高。
对石墨-方解石物料混合磨碎，由于石墨组分的动力学曲线为非线性，即Si与t有关而使得方程(1)无法得到解析解。下面作积分变换，令
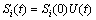(6)
再令
，即
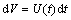(7)
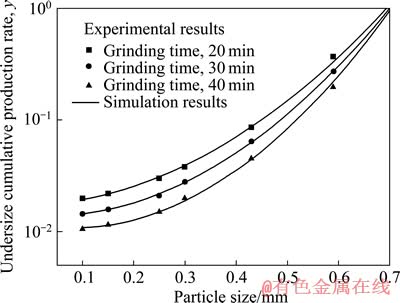
图 3 石墨单独磨碎时实验结果与模型仿真结果
Fig. 3 Testing results and simulate results of graphite grinding
将式(7)和(6)代入式(1)得
(8)
式中：Si(0)为石墨组分第i粒级的初始碎裂速率函数，对于相同粒度以及相同的配比应为常数。方程(8)的解为
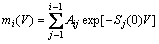(9)
式中：
(10)
对于第一粒级(最粗粒级)，式(8)变为
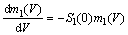(11)
解为
(12)
试验发现V与t存在下列关系：
(13)
式中：c和b均为常数。将式(13)代入式(12)得
(14)
式中：
。参数A和b可由方程式(14)求得，即将两边取两次对数后作图，即得A和b(见表1)。
表1 混合物料石墨组分的A和b参数
Table 1 Parameters A and b of graphite component of mixture
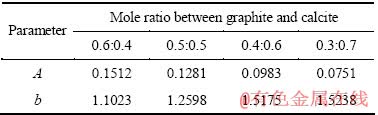
通过以上对混合物料石墨组分准线性磨碎动力学模型的建立及提出的A、b值，可以对混合物料石墨组分的磨碎结果进行模拟。图4所示为模型模拟结果与实验结果的对比。从图4可以看出，模型仿真结果和实验结果吻合度较高。
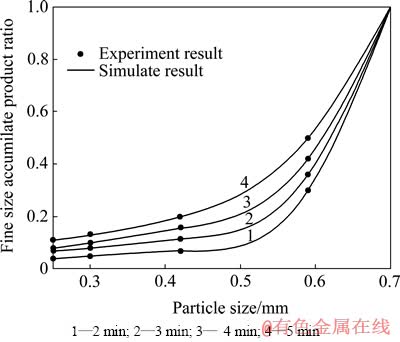
图4 石墨组分磨碎试验结果与仿真结果
Fig. 4 Experiment and simulate results of graphite component of mixture at different grinding times
2.3 碎裂分布函数bij
图5和6所示为石墨在单独磨碎和石墨-方解石物料混合磨碎时，其累积碎裂分布函数Bij与粒度xi的关系曲线。由图5和6可看出，无论是单独磨碎还是混合磨碎，石墨物料的累积碎裂分布函数Bij的变化规律基本上是相同的。考虑到实验误差的存在，可以认为：石墨物料在两种不同磨碎环境下的累积碎裂分布函数Bij是相同的。由于碎裂分布函数是可规范化 的[17]，故累积碎裂分布函数Bij相同，意味着个别碎裂分布函数bij亦相同。
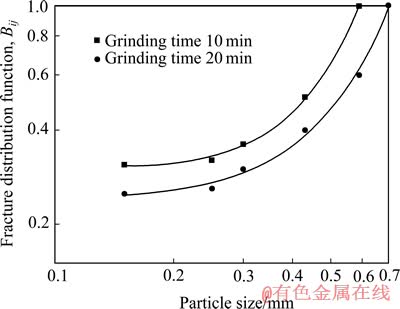
图5 石墨单独磨碎时的碎裂分布函数Bij
Fig. 5 Fracturing distribution function Bij of graphite
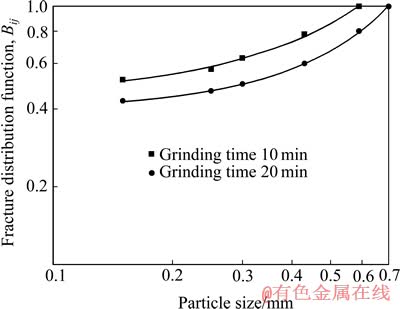
图 6 石墨组分混合磨碎时的碎裂分布函数Bij
Fig. 6 Fracturing distribution function Bij of graphite component of mixture
综上所述，不论是石墨的单独磨碎还是石墨-方解石物料的混合磨碎，被磨物料的总体积变化微小，基本上可以视为不变，故可将两种物料的混合磨碎看作是一定体积的方解石物料置换了单独磨碎时的部分石墨物料，从而改变了原来单一均质物料的磨碎环境。其结果是：一方面，由于石墨组分相对较软，而方解石组分相对较硬，故方解石组分的存在使得石墨组分的碎裂速率函数Si增大了；另一方面，由于石墨的碎裂强度远低于方解石的碎裂强度，因而当这两种物料处于同一研磨状态时，在研磨介质的作用下，石墨组分必先碎裂，从而亦表现为碎裂速率函数Si的增大。不仅如此，由于方解石组分的存在，会同时使得石墨与钢球接触碰撞的概率变小和石墨与方解石接触碰撞的概率增大，从而导致石墨的碎裂速率函数的变化呈现复杂状况，这就是混合磨碎条件下Si与时间t相关，即ln mi与时间t呈现非线性关系的原因。
在实际磨碎过程中，如果较软组分为有用成分，则较硬组分的存在会加速该有用成分的碎裂，即破坏有用物料晶体或引起过粉碎，石墨选矿的磨碎作业即是如此[18-19]。此外，本研究中查明的组分间的相互影响规律，无论对石墨生产中大鳞片石墨的保护，还是对石墨颗粒的细粒级或超细粒级磨碎加工，都具有较大的理论指导意义。
3 结论
1) 石墨单独磨碎时，其动力学行为是线性的，即同一粒级的碎裂速率函数Si为常数，且在一定的磨碎时间内，具有显著的细粒级零阶产出特征，即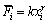
，其中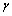
值与磨碎环境无关，只与物料的碎裂特性有关；而碎裂分布函数bij则不随时间而变化。
2) 石墨-方解石物料混合磨碎时，其中方解石组分的存在对石墨组分的碎裂分布函数bij未产生影响；但却使石墨组分的碎裂速率函数Si发生了变化，其变化规律为：石墨组分的碎裂速率函数Si不仅增大了，而且其物理特性表现为非线性。
3) 混合磨碎石墨组分的碎裂速率函数Si的准线性模型仿真结果表明，石墨组分表现的非线性碎裂结果的模拟值与实验值吻合度较高。
REFERENCES
[1] ZHAO Hai-peng, REN Jian-guo, HE Xiang-ming, LI Jiang-jun, JIANG Cheng-yin, WAN Chun-rong. Purification and carbon- film-coating of natural graphite as anode materials for Li-ion batteries[J]. Electrochimica Acta, 2007, 52(19): 6006-6011.
[2] 尹丽文. 世界石墨资源开发利用现状[J]. 国土资源情报, 2011(6): 29-32.
YIN Li-wen. Current situation of development and use of world graphite resources[J]. Land and Resources Information, 2011(6): 29-32.
[3] INAGAKI M,TOYODA M,KANG F Y,ZHENG Y P,SHEN W C. Pore structure of exfoliated graphite-A report on a joint research project under the scientific cooperation program between NSFC and JSPS[J]. New Carbon Materials, 2003, 18(4): 241-249.
[4] 崔源声, 李 辉, 徐德龙. 世界天然石墨生产、 消费与国际贸易[J]. 中国非金属矿工业导刊, 2012(4): 48-51.
CUI Yuan-sheng, LI Hui, XU De-long. Production, consumption and global trade of natural graphite[J]. China Non-metallic Mining Industry Herald, 2012(4): 48-51.
[5] 颜玲亚. 世界天然石墨资源、消费及国际贸易[J]. 中国非金属矿工业导刊, 2014(2): 33-36.
YAN Ya-ling. Graphite resources, consumption and international trade in the World[J]. China Non-metallic Mining Industry Herald, 2014(2): 33-36.
[6] 卢立丽, 王松蕊, 刘兴江. 锂离子电池电化学模拟模型的比较[J]. 电源技术, 2011, 35(7): 765-883.
LU Li-li, WANG Song-rui, LIU Xing-jang. Contrast between lithium-ion cells models[J]. Chinese Journal of Power Source, 2011, 35(7): 765-883.
[7] 沈万慈, 康飞宇, 黄正红, 杜鸿达. 石墨产业的现状与发展[J]. 中国非金属矿工业导刊, 2013(2): 1-4.
SHEN Wan-ci, KANG Fei-yu, HUANG Zheng-hong, DU Hong-da. Current situation and development of Chinese graphite industry[J]. China Non-metallic Mining Industry Herald, 2013(2): 1-4.
[8] WANG Xing, GAI Guo-sheng, YANG Yu-fen, SHEN Wan-ci. Preparation of natural microcrystalline graphite with high sphericity and narrow size distribution[J]. Powder Technology, 2008, 181(1): 51-56.
[9] 传秀云. 天然石墨矿物与储能材料[J]. 中国非金属矿工业导刊, 2013(3): 1-2.
CHUAN Xiu-yun. Natural graphite mineral and energy storage materials[J]. China Non-metallic Mining Industry Herald, 2013(3): 1-2.
[10] 龙 渊, 张国旺, 李自强, 肖 骁. 保护石墨鳞片的磨矿效果表征[J]. 中国非金属矿工业导刊, 2013(6): 32-34.
LONG Yuan, ZHANG Guo-wang, Li Zi-qiang, XIAO Xiao. The method to express protecting flaky graphite of grinding effect[J]. China Non-metallic Mining Industry Herald, 2013(6): 32-34.
[11] 龙 渊, 张国旺, 李自强, 肖 骁. 保护石墨大鳞片的工艺研究进展[J]. 中国非金属矿工业导刊, 2013(2): 44-47.
LONG Yuan, ZHANG Guo-wang, LI Zi-qiang, XIAO Xiao. Research progress of the protecting large flaky graphite[J]. China Non-metallic Mining Industry Herald, 2013(2): 44-47.
[12] REID K J. A Solution to the batch grinding equation[J]. Chemical Engineering Science, 1965, 20(11): 953-963.
[13] 孟振强, 刘如铁, 熊拥军, 赵福安, 李溪滨. 球磨方式对多壁碳纳米管形貌和结构的影响[J]. 中国有色金属学报, 2012, 22(12): 3421-3426.
MENG Zhen-qiang, LIU Ru-tie, XIONG Yong-jun, ZHAO Fu-an, LI Xi-bin. Effect of ball milling on morphology and structure of multi-walled carbon nanotubes[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(12): 3421-3426.
[14] 刘开忠, 翁伟雄, 周忠尚. 某些物料的碎裂特性及其碎裂数估计[J]. 矿冶工程, 1988, 8(3): 42-46, 57.
LIU Kai-zhong, WENG Wei-xiong, ZHOU Zhong-shang. The fracturing properties of some materials and the estimation of their fracturing parameters[J]. Mining and Metallurgical Engineering, 1988, 8(3): 42-46, 57.
[15] AUSIN L G, LUKIE P T. Estimation of non-normal breakage distribution parameter from batch grinding[J]. Power Technology, 1972, 5: 257-277.
[16] 田金星. 石墨及其混合物料的磨碎动力学行为[J]. 中国有色金属学报, 1996, 6(4): 47-50.
TIAN Jing-xing. The Grinding kinetic behaviors of graphite and its mixture[J]. The Chinese Journal of Nonferrous Metals, 1996, 6(4): 47-50.
[17] 刘开忠, 翁伟雄, 周忠尚. 混合物料组分的碎裂参数特性[J]. 中国有色金属学报, 1995, 5(2): 47-50.
LIU Kai-zhong, WENG Wei-xiong, ZHOU Zhong-shang. Fracture parameters characteristics of mixed material components[J]. The Chinese Journal of Nonferrous Metals, 1995, 5(2): 47-50.
[18] 岳成林. 鳞片石墨大片损失规律及磨浮新工艺研究[J]. 中国矿业, 2007, 16(10): 83-85.
YUE Cheng-lin. Research on the loss of big scales and a new flotation technology for scale graphite[J]. China Mining Magazine, 2007, 16 (10): 83-85.
[19] 肖伟丽. 某石墨矿提高精矿大片产率及品位的浮选工艺研究[J]. 硅谷, 2012(8): 110-111.
XIAO Wei-li. The flotation processing studying of grade and producing rate of large flaky Graphite flotation of some Graphite minerals[J]. Silicon Valley, 2012(8): 110-111.
(编辑 何学锋)
基金项目：国家“十二五”科技支撑计划项目(2013BAE04B03)
收稿日期：2014-07-28；修订日期：2014-10-13
通信作者：田金星，副教授；电话：15071076550；E-mail: tianjinxing423@sina.com
