简介概要

Ta-W合金高应变速率下亚结构转变研究进展

来源期刊：稀有金属2021年第3期

论文作者：关欣然陈强舒大禹曹国剑曲寿江崔国荣

文章页码：341 - 352

关键词：Ta-W合金;冲击诱导相变;动态再结晶;动态回复;形变孪晶;

摘要：综述了Ta-W合金在冲击载荷作用下的动态力学响应、常用研究方法及亚结构转变。其中Ta-W合金在高应变速率下常见的亚结构转变包括:冲击诱导相变、绝热剪切带中发生的动态回复及动态再结晶,以及高应变速率下的形变孪生。Ta-W合金在高应变速率下发生冲击诱导相变是合金内部位错组态与位错密度共同作用的结果,且通过实验数据与数学模拟证明了相变的发生与冲击载荷作用下存在的剪切应力密切相关;Ta-W合金绝热剪切带内的绝热升温不足,且没有足够时间通过位错的湮灭完成晶界的细化,因此仅发生动态回复作用。然而限于仪器精度条件,有关绝热剪切带形成机理及内部的亚结构转变亟待澄清;Ta-W合金高应变速率下孪生形成与孪生临界形成应力、位错组态及位错密度密切相关,计算证明孪生对于总应变量贡献较低,位错组态与位错密度在高应变速率下形变孪生中的作用机理亟待阐明。

详情信息展示

稀有金属 2021,45(03),341-352 DOI:10.13373/j.cnki.cjrm.XY20010003

Ta-W合金高应变速率下亚结构转变研究进展

关欣然陈强舒大禹曹国剑曲寿江崔国荣

哈尔滨理工大学材料科学与工程学院

中国兵器工业第五九研究所

同济大学材料科学与工程学院

哈尔滨工业大学(威海)材料科学与工程学院

摘要：

综述了Ta-W合金在冲击载荷作用下的动态力学响应、常用研究方法及亚结构转变。其中Ta-W合金在高应变速率下常见的亚结构转变包括:冲击诱导相变、绝热剪切带中发生的动态回复及动态再结晶,以及高应变速率下的形变孪生。Ta-W合金在高应变速率下发生冲击诱导相变是合金内部位错组态与位错密度共同作用的结果,且通过实验数据与数学模拟证明了相变的发生与冲击载荷作用下存在的剪切应力密切相关;Ta-W合金绝热剪切带内的绝热升温不足,且没有足够时间通过位错的湮灭完成晶界的细化,因此仅发生动态回复作用。然而限于仪器精度条件,有关绝热剪切带形成机理及内部的亚结构转变亟待澄清;Ta-W合金高应变速率下孪生形成与孪生临界形成应力、位错组态及位错密度密切相关,计算证明孪生对于总应变量贡献较低,位错组态与位错密度在高应变速率下形变孪生中的作用机理亟待阐明。

关键词：

Ta-W合金;冲击诱导相变;动态再结晶;动态回复;形变孪晶;

中图分类号： TG146.416

作者简介：关欣然(1996-),男,黑龙江哈尔滨人,硕士研究生,研究方向:钽钨合金、钛合金,E-mail:13101618335@sina.cn;*曲寿江,副教授,电话:021-39947690;E-mail:qushoujiang@tongji.edu.cn;;

收稿日期：2020-01-05

基金：国家自然科学基金项目(50961008,51061008)资助;

Research Progress of Substructure Transformation of Ta-W Alloys at High Strain Rates

Guan Xinran Chen Qiang Shu Dayu Cao Guojian Qu Shoujiang Cui Guorong

School of Materials Science and Technology,Harbin University of Science and Technology

No.59 Institute of China Ordnance Industry

School of Materials Science and Technology,Tongji University

School of Materials Science and Engineering,Harbin Institute of Technology at Weihai

Abstract：

Ta-W alloy had been gradually developed as a penetrating weapon material due to its high density,high melting point and excellent high temperature strength. The high-speed penetration of the projectile was accompanied by the transformation of the internal substructure of the material. Compared with the static loading,the high strain rate loading process involved strain,strain rate,inertia,heating,and even secondary effects such as sound,light,and electricity. The penetration process was very short,so the analysis and processing were more complicated. In the process of dynamic loading,some substructure transformations in the material were often destructive. For example,the appearance of dynamic recrystallization(DRX)might become a potential factor of adiabatic shearing phenomenon,but at the same time,the generation of twins and stress-induced martensite in titanium alloys has been experimentally proved to effectively slow down the expansion of the shear band and caused the bifurcation of the shear band. Therefore,studying the substructure transformation and mechanism of Ta-W alloy at high strain rate was of great significance to improve the penetration performance of the projectile and to better apply the material to service at high strain rate. In the study of Ta-W alloy dynamic mechanics,the split Hopkinson pressure bar(SHPB)was widely used because of its higher strain rate and reliability compared with the thickwalled cylinder implosion test(TWC)and Taylor impact test. According to the geometry of the sample,it could be pided into dynamic compression experiment of cylindrical sample,dynamic compression experiment of hat-shaped sample and dynamic compression experiment of shear compression specimens(SCS). Different loading conditions could be achieved by controlling the geometric size of the sample,which had a very obvious influence on the damage of the sample and the generation and expansion of the shear band. In the characterization of the microstructure inside the Ta-W alloy after dynamic loading,the scanning electron microscope(SEM)could observe the microstructure inside the sample more macroscopically and realize the phase distribution and fracture analysis when the sample was damaged by adjusting the backscattered electron(BSE)mode and secondary electron(SE)mode. X-ray diffraction(XRD)could analyze the phase transition of the material during the high strain rate loading process and combine with the selected area electron diffraction(SAED)to realize the phase analysis of the small area. Focused ion beam(FIB)combined with transmission electron microscope(TEM)method could achieve fixed-point observation of small areas. Compared with ordinary backscattered electron diffraction(EBSD),the transmitted electron backscatter diffraction technology(t-EBSD)had higher spatial resolution and could characterize ultra-fine grains and deformed grains. Compared with TEM technology,the inside of Ta-W alloy could be analyzed more macroscopically without losing precision. This article summarized the substructure transformation of Ta-W alloys at high strain rates from three aspects:impact-induced phase transformation,dynamic recovery(DRV)and DRX in adiabatic shear band(ASB),and deformation twinning at high strain rates. Through the analysis of the microstructure of pure tantalum,Ta-5W,Ta-10W with different tungsten contents Ta-W alloys after deformation at high strain rates,it could be found that the impact-induced phase transformation was caused by the common dislocation configuration and dislocation density in the alloy. The results of the action,and experimental data and mathematical simulations proved that the occurrence of phase transition was closely related to the shear stress under impact load. Through the dynamic loading test of the Ta-W alloy hat-shaped sample,the SAED from the matrix to the adiabatic shear zone showed that the grain refined and misorientation increased in the adiabatic shear zone. However,the calculation of adiabatic temperature rose in the adiabatic shear zone showed that the temperature rise caused by the adiabatic effect was not enough to support the final step of rotating dynamic recrystallization(RDR). The grain boundary refinement was completed through the annihilation of dislocations,so only DRV occurred. However,limited to the accuracy of the instrument,the formation mechanism of the ASB and the internal substructure transformation needed to be further studied and proved. It could be obtained by compressing the Ta-W alloys with different initial dislocation densities at different strain rates. The formation of twinning at high strain rates was the result of the combined effect of the critical twin formation stress,dislocation configuration and dislocation density. It was proved by calculation that the twin contribution to the total response variable was low,which was different from the general perception. However,the mechanism of dislocation configuration and dislocation density in deformation twinning at high strain rates and the role of dislocations in twin nucleation still needed to be elucidated. Existing problems:The specific mechanism and role of shear stress in impact-induced phase transformation in Ta-W alloys were still unclear,and the DRX and DRV mechanisms within ASB,as well as the effect of dislocation density and structure on twinning and phase transformation,needed to be further studied. The research on the dynamic mechanical response of materials at high strain rates involved experiments and theories of many interdisciplinary subjects such as mechanics,materials,physics,and multi-level combined research and analysis from macro to micro was necessary.

Keyword：

Ta-W alloy; shock-induced phase transformation; dynamic recrystallization; dynamic recovery; deformation twinning;

Received： 2020-01-05

Ta-W合金具有高密度、高熔点、优异的耐腐蚀性能 ^[1] 和良好的高温强度 ^[2] 等特点，被广泛应用于航空航天 ^[3] 及兵器工业 ^[4] 等领域中严苛工作环境中服役。鉴于Ta-W合金特殊的性能，该合金被逐渐开发应用于穿透武器材料 ^[5] ，作为穿透武器材料，其侵彻性能至关重要，侵彻深度（depth）可由式（1）决定：

式中，ρ_P，ρ_T分别为侵彻体材料密度和目标材料密度 ^[6] 。

根据式（1）选用高密度材料作为弹体材料。TaW合金作为穿透武器材料，在侵彻的过程中只有几十到几百毫秒量级，应变率可达到1×10⁴s^-1，如侵彻体以800 m?s^-1速度侵彻目标，将在穿透材料内产生20 GPa的冲击应力 ^[7,8,9] ，因此，研究Ta-W合金在高应变率下的变形行为及亚结构转变具有重要意义。

本文综述了Ta-W合金高应变速率下变形行为及亚结构转变机制，主要内容包括：（1）冲击载荷作用下Ta-W合金的变形特点及研究方法；（2)TaW合金在高应变速率下发生的冲击诱导相变（shock-induced phase transformation);(3)Ta-W合金绝热剪切带中的动态回复（dynamic recovery,DRV）及动态再结晶（dynamic recrystallization,DRX);(4）高应变速率下出现的冲击诱导孪生（shock-induced deformation twinning）。本文重点揭示高应变速率下微观组织演变规律，旨在提高TaW合金在冲击载荷作用下的使役性能。

1 冲击作用下的钽钨合金

1.1 变形特点

Ta和W为典型的体心立方（body-centered cubic,bcc）金属，两者在液态和固态条件下无限互溶 ^[10] ，因此，Ta-W合金为单相固溶体合金，在熔化温度以下不存在平衡相变 ^[11] 。根据Mecking分析 ^[12] ，材料在恒定结构下的流动应力（σ）是多种机制共同作用的结果，如式（2):

式中，σ_a为无热项由位错运动阻碍（如晶界、第二相）引起，σ₀为克服晶格摩擦所需应力是应变率和温度的函数，σ_p为热活化项代表位错同间隙原子及其他位错相互作用造成的位错储存，T为温度，ε?为应变速率，ε为应变。

式（2）中材料的流动应力由：（1）晶格阻力，（2）位错和位错之间的相互作用，（3）间隙强化和固溶强化，（4）第二相和弥散强化，（5）晶界的强化作用共同作用导致。

对于一个给定的组织，位错运动的阻碍作用可以通过热激活来降低，因此，强度会随温度的升高或应变速率的降低而降低 ^[13,14,15] 。

Gao等 ^[16] 采用准静态压缩试验和分离式霍普金森压杆（split hopkinsonpressure bar,SHPB）实验系统，研究了不同W含量的两种Ta-W合金Ta-2.5W（%，质量分数，全文同）和Ta-10W在8.3×10^-4～3.55×10³s^-1应变速率范围内的变形行为，根据实验参数拟合了Johnson-Cook本构方程，通过泰勒冲击实验对模型进行了验证。研究结果表明：Ta-W合金对应变速率和W含量敏感，对硬化指数并不敏感。随着W含量的提高，Ta-W合金的流动应力和屈服应力也随之提高，表现为明显的固溶强化作用；随着应变速率的提升，Ta-W合金的屈服强度和流动应力不断提高，呈现典型的应变率硬化现象，随着应变速率的提高，材料变形的时间降低，导致单位时间内开动位错的增加，因为没有足够的时间来给予位错进行运动，相邻晶粒的协调变形，导致材料内部应力的集中 ^[17] 。

Chen和Gray ^[18] 采用SHPB研究了应变速率、温度和W合金化对Ta屈服应力和应变硬化行为的影响，通过Zerilli-Armstrong,Johnson-Cook,MTS 3种本构方程对实验结果进行模拟。研究结果表明，W元素添加提高了Ta-W合金的屈服应力、流动应力水平和加工硬化率。流动应力表现出来的高的应变速率和温度敏感性以及应变硬化率的不敏感性表明，低中温时Ta和Ta-W合金在高应变速率下变形的控制机制是派纳力和热激活。

白润等 ^[19] 利用万能材料试验机和SHPB，在223～973 K,1×10^-4～1×10³s^-1应变速率范围内，对退火态Ta-10W合金进行了准静态和动态力学性能测试。通过分析应力-应变曲线，指出合金流动应力对应变速率和温度的变化敏感，表现出明显的应变率强化和温度软化，低温和高应变速率下表现出更大的应变速率敏感性。

Ta-W合金高应变速率下变形特点：（1）明显的应变速率和温度敏感性（如图1 ^[13] ），流变应力和屈服强度随着应变速率提高而增加，随着温度升高而降低；（2）随着Ta-W合金中W含量增加，材料流动应力和屈服强度提高，为固溶强化。NematNasser等 ^[20] 通过对Ta和Ta-2.5W合金变形行为对比，加入W增加了整体的流动应力，同时降低了材料对温度和应变率敏感性。

图1 Ta-W合金真应力-真应变曲线示意图

Fig.1 Schematic diagram of true stress-true strain curves of tantalum-tungsten alloy ^[13]

1.2 研究方法

实验加载方式对材料力学性能有显著的影响。近年来，研究者采用SHPB ^{[21,22,23,24]} ，霍普金森拉杆实验（split hopkinsontensile bar,SHTB) ^[25] ，“飞盘”实验 ^[1,26] ，厚壁筒体爆炸失效实验 ^[27,28] ，爆炸驱动冲击波恢复实验 ^{[29,30,31,32,33]} ，研究了Ta-W合金在高应变速率下的力学行为。SHPB因为自身良好的可行性，较高的应变可靠性，以及高的应变速率等优点 ^[34] ，被国内外学者广泛采用。

2 冲击诱导相变

Ta作为典型在熔点下不存在平衡固态相变的bcc金属 ^[29] ，图2为钽熔化曲线 ^[35] ，学者通过实验现象观察到：Ta和Ta-W合金在冲击载荷的作用下会发生β（bcc）→ω密排六方（hexagonal closepacked,hcp）的冲击诱导相变现象。

Hsiung等 ^[11,29,30] 利用爆炸驱动冲击波恢复实验和透射电子显微镜（transmission electron microscope,TEM) ^[11] ，对Ta,Ta-5W以及Ta-10W合金在30GPa的峰值应力作用下的亚结构转变进行分析。图3为Ta,Ta-5W,Ta-10W在30 GPa峰值应力冲击之后的TEM观察 ^[11] ，由图3可见，Ta和Ta-5W合金中没有观察到ω相的转变，只观察到在晶界处大量位错缠结，形成位错胞状结构；Ta-10W合金中观察到了ω相，同Ta,Ta-5W相比，Ta-10W位错密度大、分布均匀。Ta-10W在30 GPa峰值冲击应力作用下的TEM照片，与文献 [ 29] 中Ta在45 GPa冲击应力作用下的组织接近，观察到冲击诱导相变的现象。通过Orowan方程式（3):

图2 Ta熔化曲线

Fig.2 Melting curve of tantalum ^[35]

式中，为应变速率，Φ施密特因子（Schmid factor),b柏氏矢量，ρ为平均位错密度，vˉ位错平均运动速率 ^[29] 。

式（3）推导可知，对于给定的条件，应变速率、施密特因子、柏氏矢量均为定值，随着W含量的提高，固溶强化的作用，溶质原子与位错发生交互作用，导致位错的平均运动速率降低，位错的密度上升，每个位错之间的移动距离下降，抑制了冲击过程中发生在Ta-10W中的DRV作用。这导致了Ta-10W在同样冲击载荷作用下产生了比Ta和Ta-5W更加均匀且密度更高的位错。

ω相并不是一个标准的hcp结构，而是伪密排六方（pseudo-hexagonal close packed）结构，并通过模拟衍射斑点和实际衍射斑点进行对比进行了验证。

研究结果表明：冲击诱导相变与位错的排列和密度密切相关，β→ω的冲击诱导相变实际上是在DRV过程被抑制时变形机制的替代机制，以适应位错源被耗尽而导致的位错通量(ρvˉ)的不足。冲击应力和W含量都可以起到对位错迁移率的限制，Ta在45 GPa的冲击应力作用下发生冲击诱导相变而Ta和Ta-5W在30 GPa的冲击应力作用下并没有观察到，是因为冲击应力不足以限制DRV，这时就需要将W含量提高到10%来限制DRV过程，才能在致密均匀位错中观察到冲击诱导相变。

图3 Ta,Ta-5W,Ta-10W合金在30 GPa峰值应力冲击后TEM明场像Ta-10W均匀位错中嵌入的ω相，框选区域的高分辨照片，及[101ˉ1]ω区域的选区衍射图像

Fig.3 TEM open field images of pure Ta(a),Ta-5W(b)and Ta-10W(c)after 30 GPa peak stress impact;(c)TEM image ofωphase embedded in Ta-10W uniform dislocation(inset being selected-area diffraction pattern of[101ˉ1]_ω-zone),and(d)high-resolution TEM image of frame selected region in(c) ^[11]

Lu等 ^[36] 研究了单晶bcc结构Ta在激光冲击作用下的β→ω冲击诱导相变。研究结果表明，在3.7ns加载时间、70 GPa冲击应力下观察到了ω相变，而Hsiung和Lasilla ^[29] 观察到了在1.8μs,45 GPa冲击载荷作用下发生的相变。Cynn等 ^[37] 实验结果表明，Ta在174 GPa的静压力下没有显示出明显的平衡固态相变，随着冲击载荷的增大，ω和β相之间的能量差增大 ^[38,39] 。分子动力学模拟（molecular dynamics simulation,MDS）结果表明，hcp结构的生成伴随着晶格显著的剪切变形。

Mukherjee等 ^[39] 采用第一性原理计算（first-principles calculations,FPC）和MDS，分别研究了Ta在243 GPa静压力下和Zr-Nb在18 GPa的静压力下β和ω相的结构稳定性，计算了不同压力条件下Ta和Zr-Nb中β相和ω相之间的活化势垒。研究结果表明，β相在相同压力条件下比ω相能量稳定，并在计算的压力范围内保持稳定。

图4(a) ^[39] 为Ta中ω相对于β的总能量，图中可以看出，243 GPa静压范围内，β相较于ω在能量方面更加稳定，表明243 GPa静压范围内没有发生β→ω的相变，这与Cynn等 ^[37] 研究结果一致。通过对Ta中β相和ω相之间的活化势垒的计算分析，ω相始终是不稳定相，如图4(b) ^[39] 。

图4 243 GPa静压范围内Ta中ω相对于β相的总能量；Ta中β相和ω相的活化势垒

Fig.4 (a)Total energy ofωphase relative toβphase in Ta within the static pressure range of 243 GPa;(b)activa-tion barrier betweenβandωphases in Ta ^[39]

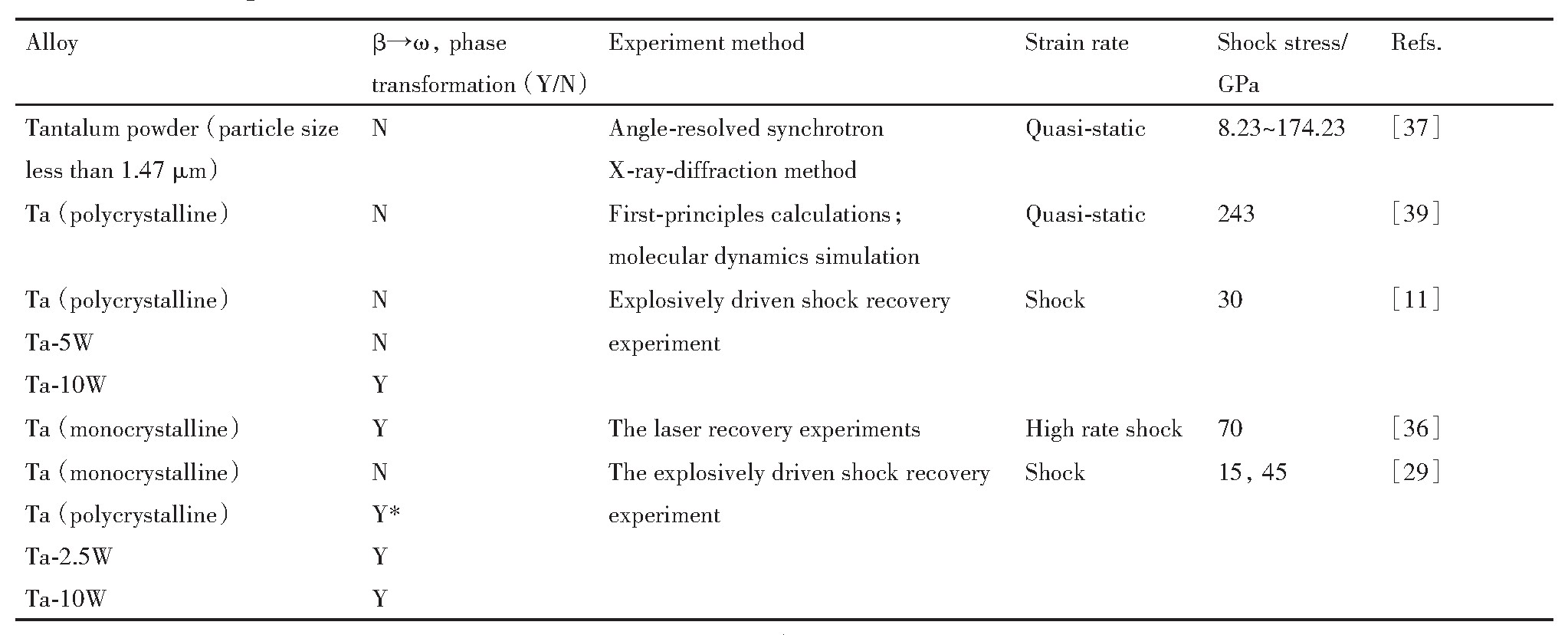
表1 Ta-W合金中相变的研究下载原图

Table 1 Study of phase transition in Ta-W alloy

*The higher volumefraction of shock-inducedωphase in Ta-W than in Ta(polycrystalline)

相的稳定性由体系自由能的高低决定。即在一个特定温度和特定压力之下，自由能最低的结构是稳定的，而所有的结构在特定条件下，都会自发地向自由能最低的结构进行转变；要发生β→ω相变，还要在冲击加载过程中满足有效能量足以克服激活势垒的条件时才会发生相变。对于Ta-10W而言 ^[11] 在冲击应力的作用下发生了平衡β→ω的过程，说明在该条件下，即30 GPa的峰值冲击应力的作用下，竞争相（ω相）的自由能低于母相（β相），而且在冲击应力的作用下体系的有效能量高于了β→ω的能量势垒，因此在Ta-W合金当中才能观察到冲击诱导相变的发生，表1为Ta-W合金相变研究的总结。

Mukherjee等 ^[39] 研究指出，ω相始终是不稳定相。在静压力高达174 GPa时，没有表现出明显的平衡固态相变；结合Lu等 ^[36] 的研究，ω相的生成伴随着晶格的显著剪切变形。冲击过程中存在的剪切应力导致了激活势垒被克服，并且在冲击加载过程中起到稳定静压力下不稳定相的作用。

Hsiung等 ^[11,29,30] 认为，冲击诱导相变与位错的排列和密度密切相关，β→ω的发生同孪晶的出现一样是一种变形的替代机制；Lu等 ^[36] ,Mukherjee等 ^[39] ,Cynn等 ^[37] 研究表明，冲击载荷中存在的剪切应力可能是导致Ta及Ta-W合金中冲击诱导相变发生的原因，然而具体的转变机制还有待进一步研究。

3 绝热剪切带中的动态回复

绝热剪切带（adiabatic shear band,ASB）是材料在高应变速率下塑性变形高度局部化的一种形式 ^[40] :(1）绝热是由于高的应变速率导致极短的变形时间，变形材料与外界没有热量交互作用，绝大部分塑性变形转化的热储存在材料内部 ^[41] ;(2）塑性变形高度局部化，在材料内部形成宽度5～100μm的窄带 ^[42] 。随着ASB形成，裂纹在ASB内部不断形核、扩展导致材料的承载能力急剧下降 ^[34,43,44] 。

Tresca等 ^[45] 于1878年首次在锤击的钢丝表面观察到“白色条带”，Zener和Hollomon ^[46] 于1944年提出“热塑失稳”解释ASB形成，2019年Guo等 ^[47] 通过实验颠覆性的观察到绝热升温发生在ASB形成之后这一现象（图5 ^[47] ），学者对该现象开展了大量研究，然而关于ASB形成机制以及内部微观组织演变仍需深入研究。

Nemat-Nasser等 ^[48] 利用SHPB结合帽形试样，在室温和600 K温度条件下，对Ta进行了应变速率超过5×10⁴s^-1的动态力学性能测试。研究结果表明，室温下ASB实验观察到DRX,600 K时，ASB中心观察到了亚晶粒和由于DRX形成的直径约为0.15μm的小晶粒，ASB的近邻位置观察到了拉长的位错胞状结构。

Nesterenko等 ^[28] 运用厚壁筒体爆炸失效实验，研究了Ta在应变速率大于1×10⁴s^-1,0～3有效应变条件下的动态力学性能。研究结果表明，不同有效应变观察到不同的微观结构，并对结构的形成进行了解释：（1）有效应变0<ε_ef<1：大量位错和位错胞状结构；（2）有效应变1<ε_ef<2:DRV形成的亚晶粒；（3）有效应变2<ε_ef<2.5：通过旋转动态再结晶（rotation dynamic recrystallization,RDRX），使得亚晶粒转变为小晶粒；（4）有效应变ε_ef>2.5：静态再结晶（static recrystallization,SRX）形成的大等轴晶粒，并通过计算对SRX过程进行了验证。

Perea-Prado等 ^[24] 利用SHPB结合帽形试样方法，研究了Ta和Ta-10W在高应变、高应变率变形时ASB组织演变规律。Ta-10W室温、3000 s^-1应变速率、剪切应变为5条件下的选区衍射图像结果表明，随着选择的区域由远离剪切带到剪切带中心，晶粒逐渐变小，晶粒之间取向差逐渐增加，这似乎印证了ASB内部发生DRX，然而背散射电子衍射（electron backscattered diffraction,EBSD）结果观察到了明显的变形织构的存在（图6 ^[24] ）。如果Ta-10W ASB内部发生DRX则所得的极图中晶粒的取向应该较为随机。

图5 商业纯Ti剪切压缩实验，时间-剪应力-温度曲线，1～8号曲线为不同探测器测量温度，并用虚线将ASB和裂纹产生的时间进行标注

Fig.5 Commercial pure Ti shear compression experiment,time shear stress temperature curve,No.1～8 curve for different detectors to measure the temperature,and use the dotted line to mark the time of ASB and crack pro-duction ^[47]

采用Zerilli-Armstrong,Johnson-Cook本构方程对Ta和Ta-10W变形过程中的升温模拟的结果表明，变形过程的绝热升温远低于Ta及Ta-W合金的再结晶温度（0.4～0.5T_m），这与之前的研究，即TaW合金ASBs内部发生DRX的现象有所不同 ^[27,28,48] 。通过有限元分析得到传统的DRX机制速度过慢，不足以在温度降低至室温这段时间内完成DRX，并提出Pri SM（亚晶粒取向转变）模型（图7 ^[24] ），以解释在高应变、高应变速率下发生在ASB中的微观结构转变（仅前4步发生）。

首先原始的晶粒在冲击载荷的作用下，位错不断增殖并在晶界处缠结形成位错胞状结构；在DRV的作用之下位错胞变得更加细小进而演变成亚晶粒；亚晶粒在冲击载荷的作用下发生旋转，随着变形程度的增加，晶粒与晶粒之间的取向差逐渐增加；最后在冷却过程中通过位错攀移的方式来实现位错的湮灭（dislocation annihilation）进而完成晶界的细化。

图6 Ta-10WSAD示意图

Fig.6 Schematic diagram of SAD image of Ta-10W ^[24]

(a)Outside shear region;(b)Close to shear region;(c)Just entering shear zone;(d)Proximity to center of ASB;(e)Center of ASB

图7 Pri SM模型

Fig.7 Pri SM model ^[24]

(a)Original crystal;(b)Elongated subgrains;(c)Rotation of subgrains;(d)High angle misorientations between some subgrains;(e)Boundary refinement

DRX需要满足温度条件，即温度达到再结晶温度（0.4～0.5T_m）；晶粒内部储存有足够的畸变能，然而从本构方程模拟中可以得到变形过程中绝热导致的温升不足以满足Ta以及Ta-W合金ASB内部发生DRX的温度要求。

Nemat-Nasser等 ^[48] ,Nesterenko等 ^[28] 均观察到了在ASB中DRX现象，然而Perea-Prado等 ^[24] 研究表明，Ta及Ta-W合金在冲击载荷加载的过程中ASBs内部不发生DRX，只发生DRV。

受制于仪器科学技术精度，学者们通常采用EBSD技术分析了ASB内部组织，然而普通EBSD难于观测位错密度较高的ASB组织，以及DRX形成了纳米尺度晶粒 ^[49,50,51] 。Lins等 ^[50] 通过集成在场发射扫描电子显微镜中的高分辨EBSD(high-resolution EBSD in a field emission gun scanning electron microscope,FEG-SEM-EBSD）观测到了ASB内部清晰的OIM图像（图8 ^[50] ）。透射式背散射电子衍射（transmission back scattering electron diffraction,tEBSD）可以分析小于50 nm的小晶粒，以及变形量大的样品 ^[52] 。这也为研究ASB的形成机制以及ASB内部的微观结构演变的研究提供了有力支持。

4 冲击诱导孪晶

近年来，国内外学者普遍关注Ta等bcc金属在高应变速率下的变形机制，尤其是形变孪生机制 ^{[6,21,25,53,54]} 。随着应变速率的增加以及温度的降低，形变孪生更容易发生 ^[55] ,bcc金属及其合金中，临界分切应力随着温度的降低而急剧升高，临界孪晶应力则随着温度的降低而有所降低 ^[13] 。尽管在大多数的温度下bcc金属及合金的变形方式还是以滑移变形为主，然在极低的温度时，临界孪晶应力会小于临界分切应力而导致bcc金属中出现孪生。

图8 通过FEG-SEM-EBSD得到的ASBs内部的OIM图像

Fig.8 OIM image inside ASBs obtained by FEG-SEM-EB-SD ^[50]

Chen等 ^[56] 运用SHPB在1×10⁴s^-1的应变速率，室温（300 K）和低温（液氮温度77 K）条件下对Ta进行了动态剪切压缩实验和单轴压缩实验。研究结果表明，单轴压缩试验表现出明显的加工硬化现象，而剪切压缩试验不仅没有明显的加工硬化趋势，反而表现出应变软化现象，而且这种现象在低温（77 K）表现的更明显（图9) ^[56] 。

TEM观察两组实验变形后的显微组织表明，剪切主导实验表现为拉长的位错胞状结构，而且其孪晶呈现边缘为锯齿状并不是典型的板状变形孪晶；在单轴压缩试验中，位错呈等轴的块状结构，变形孪晶为典型的板状结构。通过对滑移与形变孪晶相互作用的分析表明，动态剪切压缩试验促进了滑移孪晶的转化。这是因为剪切主导的压缩试验倾向于单滑移体系，这也解释了硬化的缺乏。

图9 77和300 K温度下剪切压缩试验应力应变曲线和单轴压缩试验应力应变曲线

Fig.9 Stress-strain curves of shear compression test(a)and stress-strain curves of the uniaxial compression test(b)at 77 and 300 K ^[56]

当变形条件施加的塑性应变不能完全由位错的滑移来适应时，便会发生孪生协调金属的变形，然而，Chen等 ^[21] 通过式（4）计算了孪晶能够的协调应变（ε_twin):

式中，m为施密特因子（Schmid factor,m<0.5),s为与孪晶系统相关的恒定剪切力（s=0.707),V为形变孪晶的体积分数。

通过计算在1×10⁴s^-1应变速率下ε_twin<0.03,1×10³s^-1应变速率下ε_twin<0.003，得到孪晶对于总应变的贡献很低；这与通常的认知：bcc金属具有多个滑移系统，当应变率足够高时，通常的位错机制不足以协调该速率的应变时孪晶就会发生的观点有所不同。

Florando等 ^[57] 运用伺服液压试验机、SHPB、激光冲击压缩，研究了不同应变速率（1×10^-4,1,1×10³s^-1），不同初始位错密度对Ta中的形变孪晶形成的影响。首先对没有进行预变形的试样在77 K，应变速率为1×10^-4,1,1×10³s^-1的条件下进行单轴压缩试验，发现在应变为0.7%,1.2%时并没孪晶的出现，而在5.0%,10%应变下观察到了孪晶。之后进行了不同变形量的预变形，结果表明在2%预变形后孪晶缺乏，说明孪晶随着位错密度的增加而减少，这与Mahajan和Bartlett ^[58] ,Boucher和Christian ^[59] 变形能够抑制bcc金属中孪晶的观点一致。而后对材料进行50%的变形量冷轧后，在TEM分析中观察到了位错壁结构，而且没有观察到孪晶。因为位错壁能够降低均匀变形区（homogeneous deformation zone,HDZ),HDZ越少孪晶形成所需要的应力就越大，这与Lu等 ^[60] 的观点一致。说明孪晶的形成不能用简单的孪晶临界应力来描述，达到了该应力孪晶就会形成的观点是片面的，而孪晶的形成应该是临界孪晶应力、位错结构，位错密度共同作用的结果。

Abeywardhana等 ^[61] 运用非平衡分子动力学（non-equilibrium molecular dynamics,NEMD）方法模拟了位错密度和应变速率对Ta中形变孪晶的影响。在1×10⁸～1×10¹⁰s^-1应变速率下，对Ta的完美晶体（位错密度为0）以及缺陷样品，位错密度分别为2.5×10¹¹cm^-2(low dislocation density,LDD）和2.5×10¹²cm^-2(high dislocation density,HDD）进行了准等熵压缩和膨胀模拟。结果得到HDD样品孪晶形核的应变速率阈值为2.5×10⁹～3.0×10⁹s^-1,LDD样品孪晶形核的应变速率阈值为1.0×10⁸s^-1，最大剪切应力为应变速率的函数，且遵循幂律指数：HDD为0.45,LDD为0.20。Abeywardhana等 ^[61] 通过模拟得到了同Florando等 ^[57] 相近的结果，即在高应变率下，Ta中孪晶的形成强烈依赖于位错密度和应变。