正交判别的线性局部切空间排列结合SVM的门牌识别

马立玲^{1, 2}，姬利军^{1, 2}，王军政^{1, 2}

(1. 北京理工大学 自动化学院，北京，100081；

2. 北京理工大学 复杂系统智能控制与决策教育部重点实验室，北京，100081)

摘要：为了提高门牌识别的准确率，将正交判别的线性局部切空间排列算法(ODLLTSA)和支持向量机(SVM)方法相结合用于门牌字符的识别。该方法首先通过ODLLTSA算法提取门牌字符的特征向量，然后，使用提取的特征训练SVM分类器，再应用SVM分类器对新的字符进行分类。实验结果表明：这种方法具有良好的门牌识别效果、很高的识别率、较强的鲁棒性，有较大的应用价值。

关键词：ODLLTSA算法；支持向量机；特征提取；门牌识别

中图分类号：TP391.4          文献标志码：A         文章编号：1672-7207(2011)S1-0789-05

An algorithm based on ODLLTSA and

SVM classier for door plate number recognition

MA Li-ling^{1, 2}, JI Li-jun^{1, 2}, WANG Jun-zheng^{1, 2}

(1. School of Automation, Beijing Institute of Technology, Beijing 100081, China;

2. Key Laboratory of Complex System Intelligent Control and Decision of Ministry of Education,

Beijing Institute of Technology, Beijing 100081, China)

Abstract: A new method is proposed, through combining the algorithm of orthogonal discriminant linear local tangent space alignment (ODLLTSA) and the support vector machine (SVM), to improve the accuracy of recognizing door plate numbers. The feature of door plate characters is first extracted by the ODLLTSA and then this extracted feature is used to train the SVM classifier. Finally, the new plate characters are classified by the trained SVM. Using the algorithm, a high recognition rate can be achieved. Experimental results show that this method is effective and robust in the real applications.

Key words: ODLLTSA algorithm; support vector machine; feature extraction; door plate number recognition

门牌识别技术是移动机器人视觉导航中的一项重要方法，被应用于服务机器人、侦察机器人等。门牌识别是从图像或视频中检测门牌并获取门牌号码以确定环境信息的方法。门牌识别最终是对门牌字符的识别。目前，最常用的方法有基于模板匹配方法^[1]和基于机器学习方法两大类。其中，机器学习方法主要包括支持向量机^[2]、神经网络^[3]和非参数技术等。神经网络方法由于其较强的曲线拟合以及模式分类能力，在字符识别^[4]中得到了广泛的应用。但是神经网络也有其缺点，算法训练速度较慢，而且需要较大样本进行训练分类。支持向量机(SVM)，因其能够很好地解决小样本、非线性及高维模式识别问题，在字符识别中有广泛应用。提取字符特征的方法很多，有运用纹理特征的方法，如基于局部二值模式(LBP)的方法^[5]，还有基于投影子空间的方法，其中线性方法有主元成分分析法(PCA)^[6]，非线性方法有流形(Manifold)学习方法^[7]。LBP方法过于注重局部特征，而忽视了整体特征。PCA方法从整体上考虑特征，对局部特征关注不足，而且不适合用于非线性数据。从流行学习方法中的局部切空间排列方法(LTSA)^[8]发展而来的正交判别的线性局部切空间排列方法(OLLTSA)^[9-10]能够使数据流形上类别相同且邻近的点在映射后也邻近，类别不同的邻近点在映射后远离，从而使映射后的类内散度最小，类间散度最大，而且具有保持高维数据空间测度的  性质。

在此，本文作者提出一种运用OLLTSA方法提取字符特征，然后，根据提取到的特征运用SVM分类器进行识别的门牌字符识别的方法。该方法将OLLTSA算法在特征提取上的优势与SVM分类器在小样本、非线性和高维度分类问题上的良好性能结合起来，取得了很好的效果。

1  支持向量机(SVM)原理

支持向量机的基本原理：通过事先确定的非线性映射将输入向量映射到一个高维特征空间中，在此高维空间中构建最优分类面。

设训练集，表示一个样本集，其中，n为样本特征空间的维数，y_i为样本x_i所属类别，则SVM分类器的一般形式如下：

     (1)

式中：是核函数；是通过在约束条件下，和0≤α_i≤C，i=1，…，n，求解目标函数maxQ(α)得出的，其中，C为惩罚因子。目标函数具体形式如下：

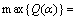
     (2)

核函数可以从原始空间中抽取特征，将原始空间的样本映射为高维特征空间中的一个向量，以解决原始空间中线性不可分的问题。只有满足Mercer条件的二元函数才能成为核函数。

常用的核函数有：(1) 高斯径向基核函数；(2) 多项式核函数，d是多项式阶数；(3) Sigmoid核函数。其中，σ，d，β，γ都是可调参数。

2  ODLLTSA算法原理

2.1  局部切空间排列(LTSA)

局部切空间排列算法(Local tangent space alignment，简称LTSA)是一种流形学习方法。通过逼近每个样本点的切空间来构建低维流形的局部几何，然后利用局部切空间排列求出整体低维嵌入坐标。

LTSA能够有效地学习出体现数据集低维流形结构的整体嵌入坐标，但是它也有一些不足：(1) 不能处理新来的样本数据；(2) 对于较大的样本集将无法进行处理。

2.2  线性局部切空间排列(LLTSA)^[9]

线性局部切空间排列LLTSA是LTSA的线性化方法，算法给出了明晰的映射关系，能够处理新的样本数据。

算法具体描述如下：

设字符流形为M^d，图像空间为R^D，字符流形上取n个样本点，，设法找到矩阵A，使得投影后的样本点，，d＜D，且满足线性映射，e是元素都为1的n维列向量。设与样本点的x_i最相近的k个点为，s_i是0-1选择矩阵，而且满足Y_i=Ys_i。

为了达到保持流形的局部几何结构的目的，应使数据的重构误差E_i 最小，那么LLTSA算法的目标函 数为

           (3)

式中：，，并且(V_i是与X_iH_n的第d个最大奇异值对应的右奇异向量。为了唯一确定Y，应该限定，其中I_d 是单位矩阵。如果考虑映射，那么目标函数就可以转化为如下形式：

              (4)

式中：。使用拉格朗日乘子法，则最优的投影向量可通过求解如下广义特征值问题得到

                (5)

如果与特征值λ₁≤λ₂≤…≤λ_d 对应的特征向量为，则LLTSA算法的转换矩阵为

                               (6)

LLTSA算法是无监督的学习算法，它没有利用样本的类别信息，还需要改进。

2.3  正交判别线性局部切空间排列(ODLLTSA)^[10]

利用类间散度矩阵对LLTSA算法的目标函数的限制条件进行修改。假设样本数据x_i属于c类中的一类，又有

              (7)

            (8)

式中：u是投影后所有样本的均值向量；u_i是投影后第i 类样本的均值向量；m_i是第i类样本的数目。

令，又因为Y=(y₁，y₂，…，y_n)=A^TXH_n，于是，则类间散度矩阵为

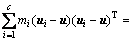
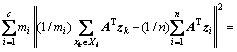
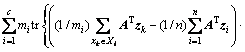
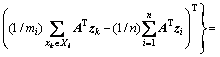
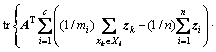
      (9)

令

，

称T_B为ODLLTSA算法的类间散度矩阵。为了使不同类别的样本被更好地识别，需要使上式最大，即

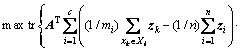
(10)

为了既能保持局部几何结构，又能使类间散度矩阵最大，得到判别的线性局部切空间排列(DLLTSA)的优化问题：

               (11)

由式(11)得出DLLTSA算法的目标函数：

        (12)

那么式(12)即转化为如下的广义特征值问题：

    (13)

DLLTSA算法的转换矩阵为。

因为矩阵A的投影向量不是正交向量，为了得到正交子空间，可使用Gram-Schmidt正交法将它们正交化，令c₁=a₁，

      (14)

令，由式(14)可知，。

令C = AL，其中，L为上三角矩阵，则ODLLTSA算法的目标函数为

   (15)

由此可知，就是ODLLTSA算法所求的转换矩阵。

ODLLTSA算法的实现：

输入：样本数据，最近邻点的个数k，降维后的维数d，样本类别标记；

输出：转换矩阵。

具体步骤：

Step1：根据最近邻点的个数k，计算点x_i(i=1, 2，…，n)的最近邻k 个点；

Step2：将X_iH_n进行奇异值分解，将它的d个最大的奇异值对应的右奇异向量组成V_i，计算；

Step3：计算排列矩阵B；

Step4：计算ODLLTSA算法的类间散度矩阵T_B；

Step5：求解广义特征值问题

，得到A= (a₁，a₂，…，a_d)；

Step6：正交化A=(a₁，a₂，…，a_d)，C =AL。

通过将样本向量和C 矩阵相乘来计算每个样本的特征向量，之后，可将这些特征向量用于分类器   构建。

3  ODLLTSA算法与SVM相结合的字符识别法

3.1  ODLLTSA法特征提取

在本文中，将样本字符图像先转换成向量，然后将所有样本字符图像转换成的向量合成矩阵，使用ODLLTSA方法处理从而得到特征映射矩阵，进而得到每幅图像的特征向量。具体方法如下：

(1) 对训练样本字符图片进行标准化处理，得到40×40的标准图像；

(2) 对标准化后的图像，将字符像素方阵以行向量优先形式转化为一个行向量，该向量维数为1 600。将所有样本的特征向量按照行排列，组成一个大矩阵，使用ODLLTSA方法处理该矩阵，得到投影矩阵C；

(3) 将(2)中得到的每个样本对应的行向量与投影矩阵T相乘得到特征向量；

(4) 根据得到的特征向量构造支持向量机，采用RBF核函数为核函数。

3.2  基于SVM分类器的识别

使用ODLLTSA方法，得到了每个样本图像的特征向量，利用特征向量构造SVM分类器，进行分类。具体方法如下：

(1) 根据得到的特征向量和类别标签构造支持向量机，采用RBF核函数为核函数；

(2) 对测试样本字符图片进行标准化处理，标准化后大小为40×40；

(3) 对标准化的图像，也将字符像素方阵以行向量优先形式转化为1 600维行向量，与投影矩阵C相乘得到特征向量；

(4) 将待识别的图像输入SVM分类器，进行识别。

整个字符识别系统框图如图1所示。

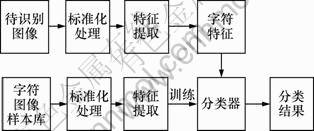
图1  门牌识别系统框图

Fig.1  Overview of door plate number recognition system

4  实验结果

本文中的仿真实验在Intel(R)Core(TM)2的的1.83GHz的PC机上进行，操作系统为Microsoft Windows XP Professional SP3，编程仿真软件为Microsoft Visual C++6.0，门牌识别MFC界面如图2  所示。

为了验证ODLLTSA算法的效果，采用已有的字符图像样本库作为样本数据进行识别实验。每个字符抽取1 000个样本训练，对惩罚因子取不同的值进行测试，发现当其取10时，分类效果较好。

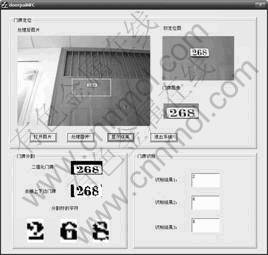
图2  门牌识别MFC软件界面

Fig.2  Software interface for door plate number recognition

图3  部分样本字符灰度图像

Fig.3  Examples of character grayscale image used in our experiments

调整所有参数到最佳，令最近邻点的个数k=d-1，其中d表示降维子空间的维数，也即特征向量的维数。对d取不同的值测试，得到维数与识别率的关系如图4所示。

另外，将本文提出的方法与PCA+SVM的方法的识别结果进行了比较。对质量为好、中、差不等的1500 幅门牌图像进行测试，对比关系如表1所列。

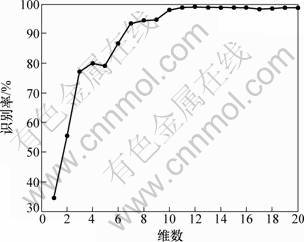
图4  维数与识别率关系图

Fig.4  Identification rates at different dimensions

表1  两种方法识别率对比

Table 1  Comparisons of identification rates between two methods

5  结论

本文提出将ODLLTSA算法与SVM分类器相结合的门牌字符识别方法，并在已有的字符样本库上进行识别实验，验证了算法的正确性和有效性。这种方法结合了ODLLTSA算法和SVM各自的优势。ODLLTSA算法不但保持了数据流形的局部几何结构，也保持了判别结构，应用于字符图像的特征提取，能很大程度地提取有效信息，并降低数据维度。而SVM在解决小样本、高维度和非线性分类问题方面有优势，将2种方法结合取得了很好的效果。由于ODLLTSA算法提取特征的有效性与邻域点个数、特征提取的维数等参数有关，如何调整这些参数，仍然需要进一步研究。

参考文献：

[1] 姜映映, 田丰, 王旭刚, 等. 基于模板匹配和SVM的草图符号自适应识别方法[J]. 计算机学报, 2009, 32(2): 252-260.
JIANG Ying-ying, TIAN Feng, WANG Xu-gang, et al. Adaptive symbol recognition for sketch-based interfaces based on template matching and SVM[J]. Chinese Journal of Computers, 2009, 32(2): 252-260.

[2] 杨晓敏, 吴炜, 黎涛, 等. 基于Gabor变换和支持向量机的车牌字符识别算法[J]. 四川大学学报: 自然科学版, 2009, 46(4): 968-972.
YANG Xiao-min, WU Wei, LI Tao, et al. An algorithm based on gabor filter and SVM for licence plate recognition[J]. Journal of Sichuan University: Engineering Science Edition, 2009, 46(4): 968-972.

[3] 陈智, 黄琳琳. 基于ICA和BP神经网络相结合的掌纹识别[J]. 北京航空航天大学学报, 2004, 34(3): 290-294.
CHEN Zhi, HUANG Lin-lin. Palmprint recognition based on ICA and BP neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 34(3): 290-294.

[4] 叶晨洲, 杨杰, 宣国荣. 车辆牌照字符识别[J]. 上海交通大学学报, 2000, 34(5): 672-675.
YEI Chen-zhou, YANG Jie, XUAN Guo-rong. Number-PLATE character recognition[J]. Journal of Shanghai Jiao Tong University, 2000, 34(5): 672-675.

[5] 郑永斌, 黄新生, 丰松江. SIFT和旋转不变LBP相结合的图像匹配算法[J]. 计算机辅助设计与图形学学报, 2010, 22(2): 286-292.
ZHENG Yong-bin, HUANG Xin-sheng, FENG Song-jiang. An image matching algorithm based on combination of SIFT and the rotation invariant LBP[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(2): 286-292.

[6] 张燕昆, 杜平, 刘重庆. 基于主元分析与支持向量机的人脸识别方法[J]. 上海交通大学学报, 2006, 36(6): 884-886.
ZHANG Yan-kun, DU Ping, LIU Chong-qing. A face recognition method based on principal component analysis and support vector machine[J]. Journal of Shanghai Jiao Tong University, 2006, 36(6): 884-886.

[7] 徐蓉, 姜峰, 姚鸿勋. 流形学习概述[J]. 智能系统学报, 2006, 1(1): 44-51.
XU Rong, JIANG Feng, YAO Hong-xun. Overview of manifold learning[J]. Transactions on Intelligent Systems, 2006, 1(1): 44-51.

[8] ZHANG Zhen-yue, ZHA Hong-yuan. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J]. Journal of Shanghai University: English Edition, 2004, 8(4): 406-424.

[9] Zhang T, Yang J, Zhao D, et al. Linear local tangent space alignment and application to face recognition[J]. Neurocomputing, 2007, 70(7/9): 1547-1553.

[10] 李勇周, 罗大庸, 刘少强. 正交判别的线性局部切空间排列的人脸识别[J]. 中国图象图形学报A, 2009, 14(11): 2311-2315.
LI Yong-zhou, LUO Da-yong, LIU Shao-qiang. Face recognition using orthogonal discriminant linear local tangent space alignment[J]. Journal of Image and Graphics, 2009, 14(11): 2311-2315.

(编辑 杨华)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：北京理工大学校内科研基地科技支撑计划项目(2011CX02010)

通信作者：马立玲(1974-)，女，河北昌黎人，博士，副教授，从事检测技术与故障诊断研究；电话：010-68912465；E-mail：maliling@bit.edu.cn