DOI: 10.11817/j.issn.1672-7207.2015.12.028
高含水老油田注采连通判别及注水量优化方法
杨超，许晓明，齐梅，李彦兰，韩洁
(中国石油勘探开发研究院，北京，100083)
摘要：探讨注采连通关系及注水量合理利用的问题。鉴于当前描述注采连通关系、优化注水量的电容电阻模型未考虑生产井间干扰和注采井合理影响范围，通过引入生产井间干扰因子和注采井影响系数矩阵对其进行改进。改进后的注采连通新模型判别注采动态连通性，并通过构建注水效率与连通系数的关系式，提出一种注水量优化调整新方法。从连通系数和注水效率2方面对新方法的可靠性进行验证，并在冀东油田高5断块进行应用。研究结果表明：与现有方法相比，新方法计算结果与生产实际数据更接近，历史拟合时间短，快捷省时，只需要现场的地面生产数据，基本数据较易获取。
关键词：电容电阻模型；注水驱油效率；注采连通性；注水量优化；井间干扰
中图分类号：TE341 文献标志码：A 文章编号：1672-7207(2015)12-4592-10
Injector-producer connectivity identification and water injection optimization of mature oil fields in high water cut period
YANG Chao, XU Xiaoming, QI Mei, LI Yanlan, HAN Jie
(PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China)
Abstract: The rational utilization of water injection and connectivity relationships between injectors and producers were discussed. Considering that the widely used CRM (capacitance resistance model), which could estimate connectivity relations and optimize water injection efficiency, did not take into account the reasonable influence radius and inter-well interference between producers, modifications were made about the basic CRM by introducing interference constant and influence coefficient matrix. Based on calculated results of revised CRM and the new purposed expression between water injection efficiency and connectivity coefficients, a new approach for optimal adjustment of water injection was presented. Credibility and usability of the new method were verified from connectivity coefficient and water injection efficiency. The new method was preliminarily applied in GAO5 fault block of Jidong Oilfield. The results show that compared with the existing methods, the new method has the following advantages: the results are closer to actual production results; history matching is fast and timesaving; the field production data are the basic data which are easy to be obtained.
Key words: CRM (capacitance resistance model); water flood efficiency; injector-producer connectivity; water injection optimization; inter-well interference
注采精细调控是有效改善高含水老油田注水效果的一项重要决策，明确注采井间连通关系是实施注采精细调控的关键。目前确定注采井间动态连通性的方法主要有2种：基于地质模型的流线模拟(SL)[1-4]和基于生产数据的电容电阻模型(CRM，captaincies- resistance model)[5-8]。流线模拟基于三维地质模型的参数场对多相流体的渗流过程进行计算，结果较准确可靠，但历史拟合需要耗费大量人力和机时，不利于工程人员快速制定注水策略。CRM模型是一种介于统计和数值模拟之间的预测方法，可以快速量化注采井间连通程度和注水见效时间，已在国外油田[9-12]多个区块应用并得到验证。CRM模型基本理念由Albertoni等[5]提出，他们通过对注采数据实施多元线性回归得出定量表征井间连通程度的连通系数，成功地判别了注采井间的连通性。此后，Gentil等[6-8]对注采连通模型进行了改进，探讨了连通系数的物理意义、注水信号的时间滞后效应等问题。在前人研究的基础上，Sayarpour等[9-10]推导出适用于三类控制体积的注采连通模型，该研究也成为目前该领域最系统的成果。Weber等[11]针对注采数据噪声对预测结果的影响，提出输入数据的预处理方法，提高了模型的收敛速度和精度。Izgec等[13]推导了适用于未见水新油田的注采连通模型。赵辉等[14-16]的研究结果与Sayarpour等[9-10]相似。Ballin等[17]对比了CRM模型和商业流线模拟计算的连通系数，提出应将2种方法综合应用的思路。但是，现有CRM模型对初始参数要求高，计算结果中存在无法真实反映油田地质特征的因素，无法有效体现生产井间干扰的影响，而且目前关于CRM模型用于优化注水量的研究较少。为此，本文作者考虑生产井间干扰及注采井间极限影响距离对其进行改进，建立注采连通新模型；以此为基础，并借鉴流线模拟的思路，推导出注水效率与连通系数的关系，进而提出一种适合高含水老油田的注采连通判别及注水量优化方法，并通过实际区块应用进行验证。
1 现有CRM模型及其局限性
目前，常用CRM模型的主要做法为：在油水两相连续性方程的基础上，建立生产井产液量与2个未知参数(连通系数和时间滞后常数)的关系，以预测产液量与实际产液量的误差为目标函数，通过求解包含未知参数约束条件的优化问题，最终得到连通系数和时间滞后系数。连通系数体现CRM模型中“电阻”的概念，可以近似为传导率的函数[8]；时间滞后常数则反映CRM模型中“电容”的概念，与弹性压缩系数和单井控制体积有关，导致注水信号滞后的因素有大注采井距、低渗区域、断层、高黏度流体、多孔介质高压缩性等[9]。
CRM模型可表示为如下的多元非线性优化问题：
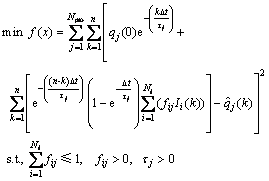(1)
式中：j=1，2，…，Npro，Npro为总生产井数；qj(0) 为生产井初始产量，m3/d；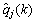
为第j口生产井第k个时间步的实测产液量，m3/d；Ii(k)为第i口注水井第k个时间步的注水量，m3/d，i=1，2，…，Ni，Ni为注水井数；τj为第j口生产井的时间滞后常数，d；fij为第i口注水井与第j口生产井间的连通系数；△t为时间步长；n为总计算时间步。
经分析发现，现有模型未考虑生产井间干扰和注采井间砂体展布影响，难以适应高含水老油田密井网开采的特点，需要建立适合高含水老油田开发特点的注采连通新模型。
2 注采连通新模型
鉴于目前注采连通模型存在的问题，并针对高含水老油田特有的开发特点，考虑生产井井间干扰的影响修正目标函数，并引入注采井间极限影响距离修正约束条件，导出高含水老油田注采连通新模型。
2.1 考虑生产井间干扰的目标函数
高含水期老油田经过多次井网加密，注采井距逐步变小，生产井间干扰对油井产液量影响较大，但由式(1)的目标函数可以看出，现有模型将每口生产井作为独立的个体考虑，并未考虑其他生产井的干扰，导致模型计算结果存在不合理性。为考虑生产井井间干扰的影响，在现有模型的基础上引入干扰因子βj (表示其他所有生产井对第j口生产井造成的干扰)，通过简单的递归计算，得第j口生产井的产液量计算公式为
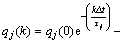
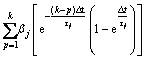(2)
从式(2)可以看出，第j口生产井第k个时间步的产液量表示为初始时刻产液量的累积效应、周围注水井注水量和周围生产井干扰3部分的综合影响，更好地体现了高含水老油田密井网开发的特点。
修正后的目标函数为
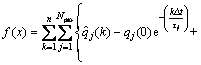
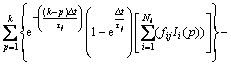
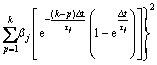(3)
2.2 考虑注采井间影响的约束条件
现有模型的计算结果中往往存在与地质认识不符的连通系数，主要表现为距离较远的注采井间存在较大的连通系数[11-12, 17]。针对该问题，本文引入极限影响距离概念，将注采井间影响系数矩阵作为连通系数的约束条件，对不合理的连通系数进行约束。
油田动态开发过程是不同时间内地层流体受到的各种驱动力和阻力共同作用的结果，地层中压力场的差异形成驱动力，当井压力波及前缘处流体受到的驱动力不足以克服阻力时，压力波停止传播而形成极限波及区域[18]。根据渗流力学不稳定渗流理论[19]，在渗透率各向异性地层中，单井的极限波及区域为椭圆形。在实际生产中存在多井干扰，将2口井(注采井对、注水井对或生产井对)的极限波及区域所形成的椭圆等压线相切时对应的井距称为极限影响距离。若井距超过极限影响距离，则认为2口井之间不存在连通关系。
储层渗透率各向异性对极限影响距离较大，储层中顺物源方向渗透率高，极限影响距离大，垂直物源方向渗透率低，极限影响半径小。下面以各向异性地层中一注一采为例计算极限影响距离(见图1)，左上方椭圆表示注水井的极限波及区域，其长半轴为a1，短半轴为b1；右下方椭圆表示生产井的极限波及区域，其长半轴为a2，短半轴为b2；θ为物源方向和注采井连线的夹角。
由图1所示的物源方向与注采井的关系，得第i口注水井与第j口生产井极限影响距离为
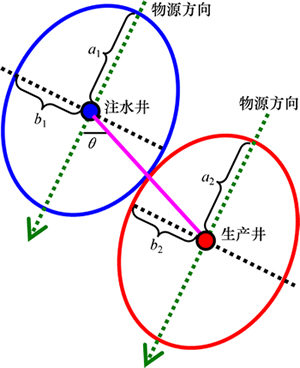
图1 极限影响距离示意图
Fig. 1 Sketch map of the maximum influence distance
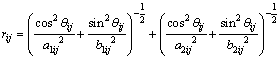(4)
式中：rij为第i口注入井与第j口生产井间的极限影响距离，m；a1ij和a2ij分别为在第i口注水井与第j口生产井形成的井对中以注水井为中心和以生产井为中心形成的椭圆的长半轴，m；b1ij和b2ij分别为在第i口注水井与第j口生产井形成的井对中以注水井为中心和以生产井为中心形成的椭圆的短半轴，m；θij为物源方向与第i口注水井和第j口生产井连线的夹角。
由各向异性地层椭圆流动方程推导[20]可得：
(5)
式中：kxij和kyij分别为第i口注水井与第j口生产井注采井对x方向和y方向绝对渗透率，10-3μm2。
在已知注采井对与物源方向夹角θ的条件下，b1ij和b2ij可采用油藏工程、数值模拟综合确定的注采合理井距之半近似，联立式(4)和(5)可计算极限影响距离。实际区块中每个注采井对与物源方向的夹角不同、各向异性渗透率不同，因此，不同注采井对的极限影响距离差别较大：处于同一沉积微相井对的极限影响距离大于处于不同相带井对的极限影响距离；处于同一沉积微相环境中的井，顺物源方向井对的极限影响距离大于垂直物源方向井对的极限影响距离。
影响系数矩阵反映了注水井对生产井的有效影响，进而可导出一个生产井数Npro、注水井数Ni的注采井组的影响系数矩阵A：
(6)
其中：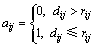
，dij为第i口注水井与第j口生产井的距离，m；rij表示第i口注入井与第j口生产井间的极限影响距离，m。
引入影响系数矩阵后，采用如下的连通系数约束条件：
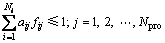(7)
2.3 注采连通新模型建立
修正的目标函数(3)、约束条件(7)以及参数非负约束条件构成高含水老油田注采连通新模型：
(8)
注采连通新模型为多参数约束非线性优化问题，拟合误差采用0.1，即满足min f(x)≤0.1时的注采井间连通系数、时间滞后常数、生产井间干扰因子为目标函数最优解。该类非线性问题的收敛性和结果的准确性在很大程度上取决于初始值是否合理。本文采用地质统计学中逆距离权方法(反映储层静态连通性)对连通系数进行初始化，并通过拟牛顿算法[14]求解CRMT无约束优化模型[9-10, 16]得到时滞常数τ的初始值。设置合理的初始参数后，通过序列二次规划方法进行迭代计算。
新模型通过注采井间连通系数、时间滞后常数、生产井间干扰因子三者结合对注采井间连通状况进行判别，增强了高含水油田注采井间连通状况判别的合理性。
3 注水量优化调整方法
为了实现区块整体注水效率的最大化，提高采收率，将高含水后期处于无效、低效注采连通关系中的注水量与高效注采连通关系中的注水量进行重新调整。
以本文所建立注采连通新模型计算的连通系数为基础，通过构建基于连通系数的注水效率关系式，计算注水效率，并以区块平均注水效率为判别标准，对比计算注水效率与区块平均注水效率确定注水量调整权重，优化调整注水井的注水量。
3.1 基于连通系数的注水效率计算
注水效率定义为某注水井周围生产井的受效产油量与该注水井注水量之比，即：
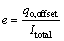(9)
式中：e为注水井注水效率；qo,offset为周围生产井的受效产油量，m3/d，通过注采连通新模型计算的连通系数计算；Itotal为注水井的总注水量，m3/d。
图2(a)所示为2个正方形五点法单元构成的6注2采井组的以注水井为中心计算的连通关系示意图，图2(b)所示为注采平衡状态下对应的流线分布示意图。以5号注水井为例，分析注水效率与以注水井为中心的连通系数的关系。已知5号注水井注水量为I5，周围仅存在2口生产井P1和P2，其产油量分别为Qo1和Qo2。
需要注意的是，本文方法计算的连通系数是用于确定注水井对周围生产井的配水量，而计算注水井周围生产井的受效产油量，需要将焦点转移到以生产井为中心的井组。
为解决该问题，文献[2-3]提出采用流线模拟计算以生产井为中心的分配系数的思路，流线模拟分配流量的基本依据是固定每条流线上的体积流量而使流线条数随注入井流量发生变化，这样在流速高的区域就可以追踪到较多数量的流线，而在流速低的区域追踪到的流线条数较少。因此，在每条流线上流量相等的条件下，通过追踪流线条数即可求得生产井流到各注水井的产油量，即受效产油量。若流线上流量不等，则需通过流量进行计算。根据图2(b)流线分布，并假设每条流线上流量相等，分别计算了以注水井和生产井为中心的连通系数，例如，5号注水井流到生产井P1和P2比例分别为2/5和3/5，而生产井P1和P2的产油量中则分别有2/12和3/11由5号注水井贡献。根据注水效率定义，计算5号注水井注水效率为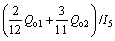
。借鉴流线模拟计算注水效率的思路，并考虑到注水量对周围生产井受效产油量的影响，导出5号注水井的注水效率与本文方法计算连通系数的关系为
(10)
对于生产井数Npro、注水井数Ni的区块，第i口注水井的注水效率为
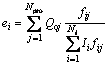(11)
式中：Ii为第i口注水井的注水量，m3/d；Qoj为第j口生产井的产油量，m3/d；Npro和Ni分别为区块的总生产井数和总注水井数。该式将注水效率与连通系数建立起联系，为注水量的优化调整提供了便利。
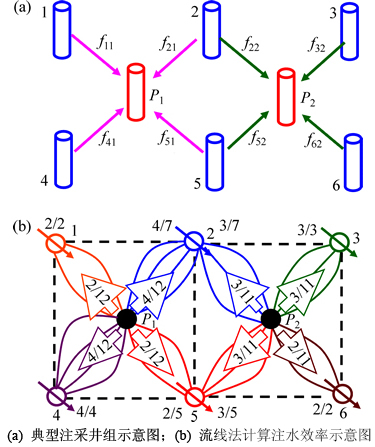
图2 注水效率与连通系数关系示意图
Fig. 2 Sketch map of relationship between injection efficiency and connectivity
另外，计算注水效率还需要确定区块平均注水效率(
)，即为所有生产井产油量之和与所有注水井注水量之和的比值。区块平均注水效率在给定时间段内是定值，为计算方便和消除流量的计量误差，区块平均注水效率采用该时间段内累计产油量与累计注水量的比值近似。
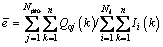(12)
式中：Qoj(k)为第j口生产井第k个时间步的产油量，m3/d。
3.2 注水量优化调整
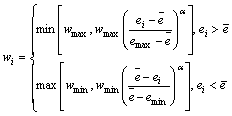
注水量调整权重是注水量优化调整的关键，权重决定了注水量调整幅度。为了增加高效注水井注水量、降低低效注水井注水量，权重应满足以下条件：注水效率高于平均注水效率的注水井的权重大于0，低于平均注水效率的注水井的权重小于0。注水量调整权重采用如下公式：
(13)
式中：α为权重变化指数，需要参考区块平均注水效率确定[2]，选取注水效率最小值emin=0.1，最大值emax=0.9；权重最小值wmin=-0.3，最大值wmax=0.3。根据参数α随权重的变化曲线，本文选取参数α=2。
根据式(13)可确定每口注水井的注水量调整权重，则调整后的注水量为：
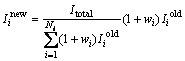(14)
式中：wi为第i口注水井的注水量调整权重；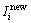
为优化后第i口注水井的注水量，m3/d；
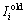为优化前第i口注水井流到第j口生产井的注水量，m3/d；Itotal为区块实测总注水量，m3/d。
4 注采连通识别及注水量优化流程
新方法应用步骤为：先用新模型求解连通系数，然后用注水效率与连通系数关系式求解注水效率，再根据以注水效率计算权重的公式，对高含水老油田各水井的注水量进行优化计算。计算流程图见图3。
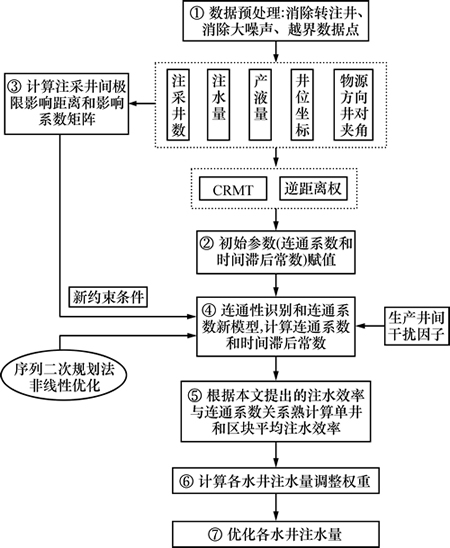
图3 新方法计算流程图
Fig. 3 Flow chart of new method
5 验证和应用
冀东油田高5断块为已开采20 a的扇三角洲沉积中孔、低渗高含水断块砂岩油藏，目前水驱控制程度和动用程度都较低，注入水单层突进现象严重，注水效率低，产油量递减快。选取主力注采井组进行研究，该井组总井数28口，其中：生产井17口，注入井5口，转注井6口，开始生产时间为1992-01，数据采集截止时间为2012-03，时间步长为1月。根据各井的生产数据及地质静态数据计算统计出各注入井的注水量、各生产井的产液量、物源方向(油藏内砂体沉积的方向)与注采井间连线的夹角、注采井之间的距离、注采井间在X和Y方向的平均渗透率和注采井间平均渗透率等数据。按照图3所示流程进行注采动态连通关系验证和注水量优化。
从连通系数和注水效率2个方面对新方法的可靠性进行了验证。首先，通过与商业流线模拟器(FRONTSIM)计算连通系数对比，验证本文注采连通新模型反演连通系数的可靠性；然后根据实际区块注水井的射孔和吸水剖面数据，验证注水量优化结果。
5.1 注采连通判别及验证
为了验证本文注采连通新模型的可靠性，将本文模型计算的连通系数与商业流线模拟器(FRONTSIM)进行对比分析，并分析生产井间干扰因子和影响系数矩阵的合理性。
求解式(8)所示优化问题，得注采连通系数矩阵见表1、时间滞后常数和生产井间干扰因子见表2。
表1 注采井间连通系数矩阵
Table 1 Injector-producer connectivity matrix
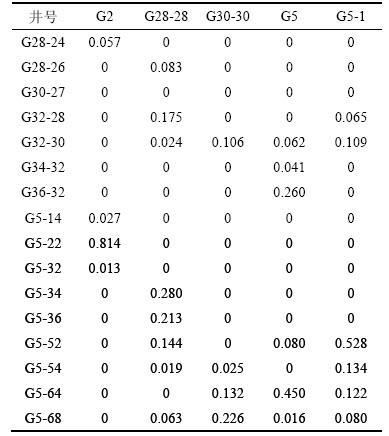
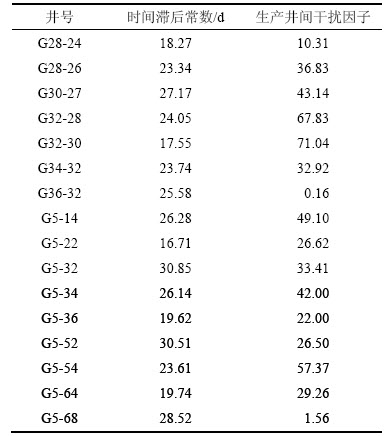
表2 注采井间滞后常数和生产井间干扰因子
Table 2 Injector-producer hysteresis constant and interference factor
将表1中的连通系数在注采井分布图上通过粗细程度不同的线将注采井相连接。注采井间连通系数越大，线条越粗，绘制成如图4所示的注采井间连通系数分布图，并与现有模型、商业流线模拟器计算的连通系数分布进行对比。图5所示为3种方法计算的研究区所有注采井对的连通系数对比。从图4和5可以看出：与现有模型对比(与流线模拟值的平均相对误差19.3%)，本文模型计算连通系数分布与流线模拟吻合较好，分析两者最大绝对误差为0.238，最小绝对误差0.015，平均相对误差为9.6%，表明本文模型对连通系数反演可靠，结果更符合地下油藏流动特征。
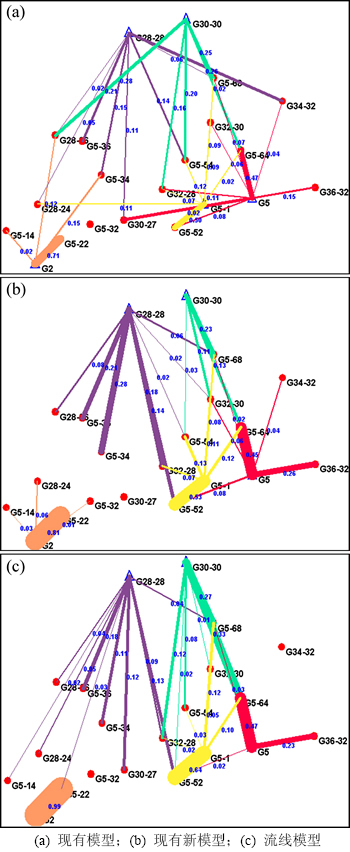
图4 现有模型、注采连通新模型和流线模拟计算连通系数分布图
Fig. 4 Connectivity map calculated by original model, new model and streamline simulation
通过分析流线模拟的计算结果发现，距离较远的井对间仍可能存在较好的连通性。这是由于处于同一沉积微相环境中的2口井，顺物源方向流动阻力小，尽管距离较远，也能形成较好的注采对应。例如，流线模拟计算的注水井G28-28与生产井G30-27的连通系数为0.118，但在井位图上两井距离为536 m，远大于式(4)计算的极限影响距离420 m，由于采用了影响系数矩阵约束，注采连通新模型计算两井间不存在连通性，故导致本文模型与流线模拟计算连通系数存在微小差异。
另外，相对于本文模型，商业流线模拟器可以很好地考虑关井、转注等生产过程中频繁变化的工作制度对流动的影响，这也是造成本文模型与流线模拟存在差异的一个重要原因。尽管流线模拟计算结果较可靠，但需要大量工程生产数据、长期繁琐的历史拟合和复杂地质模型带来的计算收敛性差等问题，而本文模型可节省大量历史拟合时间，整个拟合过程在1 h内完成，具有快速预测能力。
图6所示为注采连通新模型对区块以及典型单井产液量拟合情况。从区块产液量拟合看，预测区块产液量总体趋势上与实测值吻合，分析拟合相对误差小于10%，满足精度要求，表明对连通系数和时间滞后常数采用不同方法初始化是有效的。从单井产液量拟合效果看，引入生产井间干扰因子后产液量拟合效果更好，拟合相关系数从76.3%提高到93.2%，表明周围生产井对该井造成了干扰，拟合得到干扰因子为36.8。良好的拟合效果表明新模型能更好地体现老油田井距小、生产井间干扰严重的生产特征。
基于研究井组砂体展布、物源方向与注采井夹角以及综合方法确定的合理井距，采用式(6)确定注采井间的影响系数矩阵(表3)。图7所示为考虑注采井间极限影响距离和不考虑注采井间极限影响距离2种情况下计算的所有注采井对的连通系数。从图7可以看出：当注采井距未超过极限影响距离时，考虑和不考虑影响系数矩阵计算的连通系数基本是一致的，G2-G5-22井对的连通系数绝对误差最大为0.12，其余井对的绝对误差均在7%以下，与文献[17]中的结果一致；当注采井距超过极限影响距离时，引入影响系数矩阵后可消除不合理的连通系数，计算结果更加符合地质实际。
5.2 注水量优化及验证
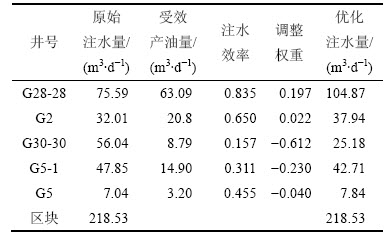
由式(12)计算该井组平均注水效率为55.6%，进而采用式(11)计算每口注水井的注水效率，通过式(13)计算注水量调整权重，最后采用式(14)确定优化后的注水量。优化注水量见表4。
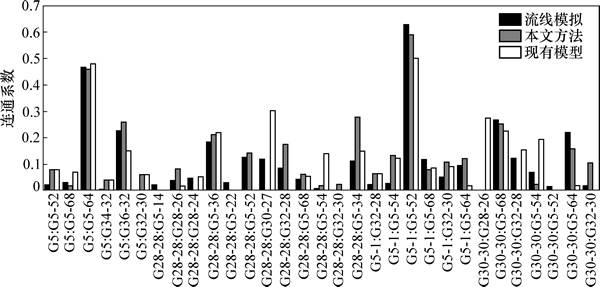
图5 注采连通新模型与现有模型、流线模拟计算连通系数对比
Fig. 5 Connectivity comparisons between original mode, new model and streamline simulation
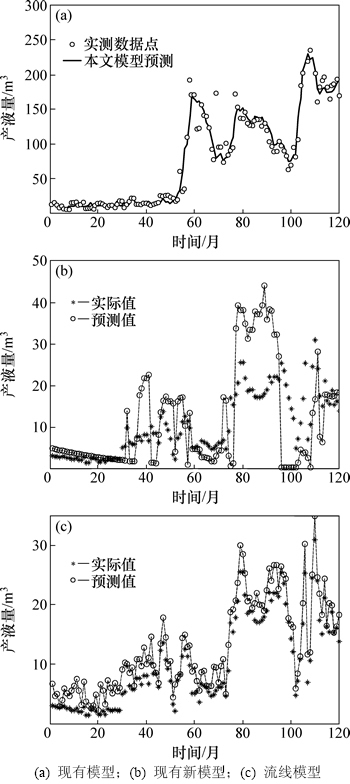
图6 生产井间干扰对历史产液量拟合效果
Fig. 6 Field liquid production matching liquid production matching with and without inference constant
表3 注采井间的影响系数矩阵
Table 3 Influence matrix of injector-producer
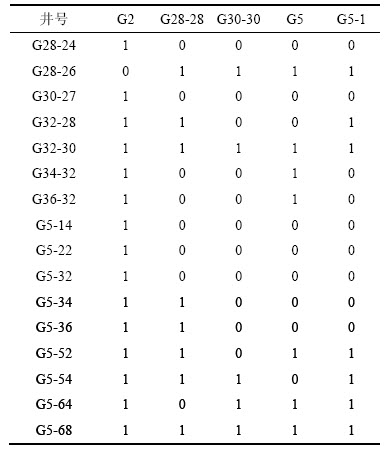
图8所示为新方法计算的高5断块5口注水井的注水效率。图中虚线为注水效率分别为25%，30%，75%和100%的界线。从图8可以看出，注水井G28-28井注水效率最高为83.5%，实际注水量远低于优化注水量，后续调整中应适当提高其注水量；G30-30井实际注水量为56 m3/d，但与周围油井连通性差或射孔不对应，大量注入水未对相关油井起到有效驱替作用，导致注水效率低，仅为15.7%，应针对该井进行注采层位调整，避免增加不必要的注水费用。G5井于2010年转注，具有注水时间短、注水量小、产油量小的特点，目前该井的注水效率为45.5%，应继续加强对G5井的动态监测。
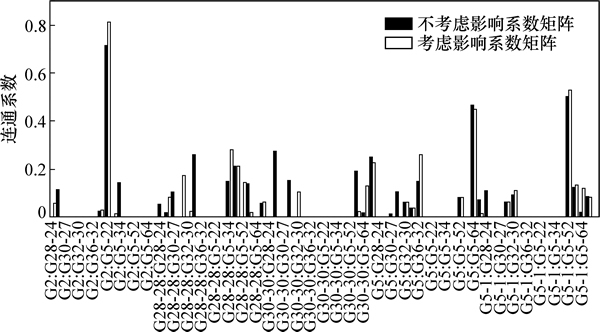
图7 影响系数矩阵对注采连通关系的影响
Fig. 7 Effect of influence matrix on injector-producer connectivity
表4 研究井组注水量优化调整
Table 4 Injection optimization of studied well group
采用数值模拟和典型注水井生产动态分析2种方法验证优化注水效率和注水量的可靠性。
在该井组历史拟合模型的基础上，采用数值模拟预测原始方案和注水量优化后5 a的开发动态，结果表明注水优化后扩大了井组整体注水波及体积，有效控制了含水率上升，提高了采出程度。相对于原始方案，0.5，1，3和5 a采出程度分别增加1.1%，1.9%，2.9%和3.3%，含水率分别降低1.3%，-0.2%(上升)，1.1%和1.9%，表明新方法优化的注水效率和注水量 可靠。
进一步以该注采井组典型注水井G30-30为例解剖。新方法计算G30-30井的注水效率较低，仅为15.7%。从G30-30井吸水情况与周围油井射孔对应情况(图9)可以看出：该水井在Ⅳ-4小层为主要吸水层，而该层周围油井并无射孔，该井注入水主要流向无相应油井射孔层位，故从油藏工程角度分析也说明该井注水效果差。因此，新方法计算结果与典型井的生产实际结果(G30-30井的吸水剖面及射孔资料)较为吻合，表明新方法是可信的。
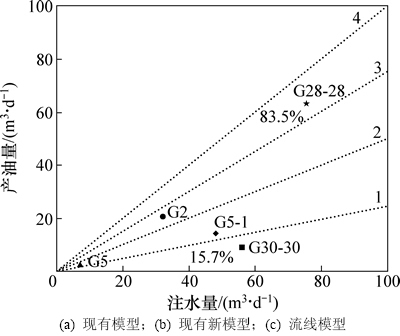
图8 注水井注水效率图版
Fig. 8 Injection efficiency of injection wells
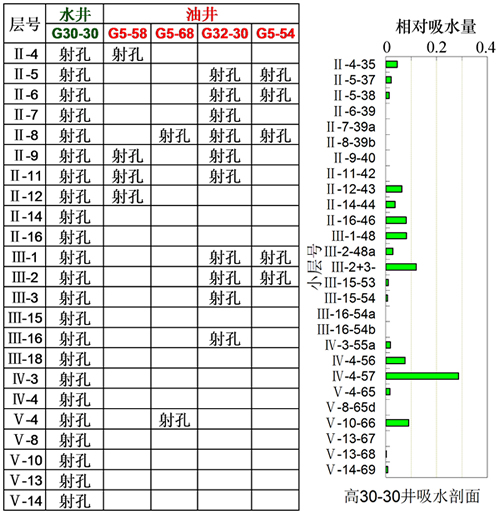
图9 典型井G30-30井射孔层位与吸水剖面图
Fig. 9 Perforation zone and intake profile of typical well G30-30
6 结论
1) 提出一种高含水老油田注采连通识别及注水量综合优化方法。新方法考虑了生产井间干扰和注采井间极限影响距离对注采连通性的影响，可用于有效判别开发后期的注采井间动态连通状况，为老油田精细注采调控和调整方案的制定提供指导。
2) 新方法计算结果与生产实际结果更接近，更符合砂体静态连通性的认识；历史拟合时间短、快捷省时；基本数据条件不苛刻，只需要现场的地面生产数据，较易获取。
3) 新方法在冀东油田高5断块进行初步应用，表明该方法对实际资料具有适用性，对实际区块注采动态连通判别及注水量优化调整具有有效性。
参考文献：
[1] Batycky R, Thiele M, Baker R, et al. Revisiting reservoir flood-surveillance methods using streamlines[J]. Spe Reservoir Evaluation & Engineering, 2005, 11(2): 387-394.
[2] Thiele M R, Batycky R P. Using streamline-derived injection efficiencies for improved waterflood management[J]. Society of Petroleum Engineers, 2006, 9(2): 187-196.
[3] Thiele M R, Batycky R P, Fenwick D H. Streamline simulation for modern reservoir-engineering workflows[J]. Journal of Petroleum Technology, 2010, 62(1): 64-70.
[4] Al-Najem A A, Siddiqui S. Soliman M. Streamline simulation technology: Evolution and recent trends[C]//SPE Saudi Arabia Section Technical Symposium and Exhibition. Al-Khobar: Society of Petroleum Engineers, 2012: 938-960.
[5] Albertoni A, Lake L W. Inferring interwell connectivity only from well-rate fluctuations in water floods[J]. Spe Reservoir Evaluation & Engineering, 2003, 6(1): 6-16.
[6] Gentil P H. The use of multilinear regression models in patterned waterfloods: Physical meaning of the regression coefficients[D]. Austin: The University of Texas at Austin, 2005: 82-99.
[7] Yousef A A, Gentil P H, Jensen J L, et al. A capacitance model to infer interwell connectivity form production and injection rate fluctuations[J]. Spe Reservoir Evaluation & Engineering, 2006, 9(6): 630-646.
[8] Lake L W, Liang X, Edgar T F, et al. Optimization of oil production in a reservoir based on capacitance model of production and injection rates[C]//Hydrocarbon Economics & Evaluation Symposium, 2007: 323-345.
[9] Sayarpour M, Zuluaga E, Kabir C S, et al. The use of capacitance-resistive models for rapid estimation of waterflood performance and optimization[J]. Journal of Petroleum Science and Engineering, 2009, 69(3/4): 227-238.
[10] Sayarpour M. Development and application of capacitance-resistive models in water/CO2 floods[D]. Austin: The University of Texas at Austin, 2008: 22-60.
[11] Weber D, Edgar T, Lake L, et al. Improvements in capacitance-resistive modeling and optimization of large scale reservoirs[C]//Proceedings of the SPE Western Regional Meeting. San Jose: Society of Petroleum Engineers, 2009: 687-702.
[12] Nguyen A, Lasdon L S, Lake L W. Capacitance resistive model application to optimize waterflood in a west texas field[C]//SPE Annual Technical Conference and Exhibition. Denver: Society of Petroleum Engineers, 2011: 1576-1592.
[13] Izgec O, Kabir C S.Understanding reservoir connectivity in waterfloods before breakthrough[J]. Journal of Petroleum Science and Engineering, 2010, 75(1/2): 1-12.
[14] 赵辉, 李阳, 高达, 等. 基于系统分析方法的油藏井间动态连通性研究[J]. 石油学报, 2010, 31(4): 633-636.
ZHAO Hui, LI Yang, GAO Da, et al. Study on reservoir interwell dynamic connectivity based on systemic analysis method[J]. Acta Petrolei Sinica, 2010, 31(4): 633-636.
[15] 赵辉, 姚军, 吕爱民, 等. 利用注采开发数据反演油藏井间动态连通性[J]. 中国石油大学学报(自然科学版), 2010, 34(6): 91-98.
ZHAO Hui, YAO Jun, L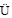
Aimin, et al. Reservoir interwell dynamic connectivity inversion based on injection and production data[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(6): 91-98.
[16] CHEN Huan, ZHANG Zhihong, SUN Wenjie, et al. Modification of capacitance-resistive model for estimating waterflood performance[C]//International Oil and Gas Conference and Exhibition. Beijing: Society of Petroleum Engineers, 2010: 517-528.
[17] Ballin P R, Shirzadi S, Ziegel E. Waterflood Management Based on Well Allocation Factors for Improved Sweep Efficiency: Model Based or Data Based?[C]//SPE Western Regional Meeting. Bakersfield:Society of Petroleum Engineers, 2012: 747-754.
[18] 卞晓冰, 张士诚, 马新仿, 等. 考虑非达西流的低渗透油藏水力压裂优化研究[J]. 中国石油大学学报(自然科学版), 2012, 36(3): 115-120.
BIAN Xiaobing, ZHANG Shicheng, MA Xinfang, et al. Optimization of hydraulic fracturing considering non-Darcy flow in low permeability reservoirs[J]. Journal of China University of Petroleum (Edition of Natural Science), 2012, 36(3): 115-120.
[19] 葛家理. 现代油藏渗流力学原理[M]. 北京: 石油工业出版社, 2003: 138-151.
GE Jiali. The modern mechanics of fluids flow in oil reservoir[M]. Beijing: Petroleum Industry Press, 2013: 138-151.
[20] Olorunwa A, Tiab D. Well test analysis in naturally fractured reservoirs using elliptical flow[D]. Oklahoma: University of Oklahoma, 2008: 105-112.
(编辑 赵俊)
收稿日期：2015-01-17；修回日期：2015-03-14
基金项目(Foundation item)：国家科技重大专项(2011ZX05010-002)(Project (2011ZX05010-002) supported by the National Science and Technology Major Program of China)
通信作者：杨超，博士，工程师，从事高含水老油田开发理论和海外新项目开发工程评价工作；E-mail：yangchao2010phd@163.com
