极小样本下高速列车轴承的可靠性评估
朱德馨,刘宏昭
(西安理工大学 机械与精密仪器工程学院,陕西 西安,710048)
摘要:针对高速列车轴承在极小样本零失效情况下的可靠性试验评估问题,采用Bayes数据统计理论将先验信息与试验信息进行融合,建立累积失效概率数学模型,根据最小二乘法求解出二参数威布尔分布中的待定参数,得出高速列车轴承可靠性数学模型。研究结果为评估高速列车轴承的可靠性和运行安全性提供了一定的理论依据。
关键词:高速列车轴承;极小样本;可靠性评估;Bayes方法
中图分类号:TH122 文献标志码:A 文章编号:1672-7207(2013)03-0963-07
Reliability evaluation of high-speed train bearing with minimum sample
ZHU Dexin, LIU Hongzhao
(Faculty of Mechanical and Precision Instrumental Engineering, Xi’an University of Technology, Xi’an 710048, China)
Abstract: For the problem of reliability evaluation about the high-speed train bearings in the case of minimum sample and zero-failure reliability test evaluation, the prior information and the experimental information were fused using Bayes data statistical theory, and the mathematical model of the accumulation failure probability was established. According to the least square method, the undetermined parameters of the two parameter Weibull distribution were solved and the reliability mathematical model was obtained about the high-speed train bearing. The results show that the problem of the high-speed train bearing’s reliability evaluation is worked out in the minimum sample and zero-failure situation and a method is provided for evaluating the high-speed train bearing's reliability and the safety.
Key words: high-speed train bearing; minimum sample; reliability evaluation; Bayes method
作为高速铁路客车行走支承的重要部件,轴承的精度、寿命、可靠性等指标对高速铁路客车的性能和安全性起着至关重要的作用。因此,为分析和评价新研发的高速列车轴承产品是否满足规定的可靠性要求,就需要对可靠性试验进行评估。对于可靠性试验,一般是通过定数或定时截尾来获得试验数据。在定数截尾试验中,由于受到实际试验条件的限制,要让一些长寿命的试验样品进行到第n个样品失效,需要花费很长的试验时间。但在定时截尾试验中,又往往会遇到在停止试验之前没有样品失效的情况。随着科学技术的进步,人们对产品质量的要求越来越高,产品的可靠性也越来越高,所以在可靠性寿命试验中,这种“无失效数据”的现象也越来越多,特别是在高可靠性、小样本问题中,更容易产生无失效数据。由于高速列车轴承造价昂贵、精度和可靠性要求极高等问题,在进行可靠性寿命试验时,不可能做样品的完全失效试验,也不可能利用大样本数据来进行试验,只能做小样本甚至是极小样本、短时间内的定时截尾试验。在这种情况下,如若再采用建立在大样本之下的经典概率统计方法来评估其可靠性,很难获得较为准确的结果。因此,如何充分利用有限的信息来寻求一套适合于高速列车轴承可靠性评估的小样本方法成为目前急需解决的一个重要问题。在小样本条件下,为提高可靠性的评估精度,最有效的途径就是设法增加信息量。目前,Bootstrap方法、修正极大似然估计法、Bayes法等已被用于对小样本产品可靠性的评估[1-6]。其中Bayes方法由于能充分利用现存的所有信息,不但可减少因样本少而带来的统计误差,而且在无失效数据样本的条件下也可对被测量进行估计,因此,近年来该方法在可靠性研究中得到了越来越多的关注和应用[7-12]。陈文华等[10]利用Gamma分布作为先验分布,以失效率为验证指标,讨论了Weibull分布下产品可靠性的Bayes验证试验设计方法;Lou等[11]采用无信息先验分布的Bayes方法提出了小样本下滚动轴承寿命参数的点估计和区间估计方法;楼洪梁等[12]根据Bayes方法,给出了小样本少失效的情况下滚动轴承可靠性的定量评价方法。在此基础上,本文作者将Bayes方法应用到高速列车轴承的可靠性评估中,采用定时截尾试验数据,以累积失效概率为指标、Beta分布为先验分布,将先验信息与仿真试验信息进行融合,建立起累积失效概率模型,并依据最小二乘法估计出Weibull分布的2个未知参数,得出极小样本无失效情况下的高速列车轴承的可靠性数学模型。在给定的可靠度要求下,求解出轴承的可靠性寿命,从而为评估高速列车轴承的可靠性和运行安全性提供了一定的指导依据。
1 高速列车轴承的可靠性模型
在各种分布理论中,由于Weibull分布更接近寿命试验结果,因此,假定高速列车所采用的双列圆锥滚子轴承寿命服从二参数Weibull分布,
即
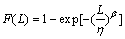 (1)
(1)
其中:F(L)为轴承的累积失效概率;L为轴承的寿命随机变量;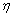 为尺度参数或轴承的特征寿命;
为尺度参数或轴承的特征寿命; 为形状参数。
为形状参数。
其可靠度函数为
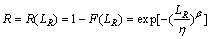 (2)
(2)
其中:LR为可靠度为R时的寿命。
由式(1)可知,欲确定高速列车轴承的可靠性寿命,必先确定参数 和
和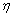 。通常需要经大量的疲劳寿命试验获得其估计值。然而,由于缺少高速列车轴承现场数据及试验数据,难以确定其准确值,因此,需借助于小样本情况下的Bayes可靠性评估方法。
。通常需要经大量的疲劳寿命试验获得其估计值。然而,由于缺少高速列车轴承现场数据及试验数据,难以确定其准确值,因此,需借助于小样本情况下的Bayes可靠性评估方法。
2 Bayes可靠性评估方法
Bayes可靠性评估[13]是一种综合经验信息进行可靠性评估的方法。其最基本的观点就是假设任一未知量θ都可看作是一个随机变量,应该用一个概率分布描述对θ的未知状况。而这个概率分布在抽样前就有关于θ的先验信息的概率陈述,因此,这一概率分布被称为先验分布。有了这个先验分布,从而不需要很大的样本就可以得到较好的估计,这正是Bayes统计方法的优点所在。
2.1 极小样本定时截尾下的无失效数据
从产品中随机选取一组用来试验的n(n≤2)个样本,对该组样本进行k次定时截尾寿命试验,截尾时间依次为t1,t2,…, tk,在第i次截尾之前仍未失效的样本数记为ni,则n1=n。若试验结束时样本都没有发生失效,则得到如下数据:
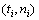 i=1, 2, …, k
i=1, 2, …, k
全部样本的无失效数据可表示为:
 i=1, 2, …, k
i=1, 2, …, k
其中: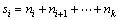 ,相当于k次定时截尾试验中截止时刻ti时共有si个样本参加试验。
,相当于k次定时截尾试验中截止时刻ti时共有si个样本参加试验。
2.2 累积失效概率pi的多层Bayes分析
由于在做定时截尾寿命试验时可获得一组数据(t1, n1),(t2, n2),…,(tk, nk),因此,对应于每个截尾时刻t1,t2,…,tk下的累积失效概率可分别记为p1,p2,…,pk。
在已知ti时刻的累积失效概率pi的条件下,由二项式分布定理可知,si件样本中有ri件失效的概率为:
 (3)
(3)
其中: 表示si件样本中有ri件失效的组合。特别地,当ri=0时,则有
表示si件样本中有ri件失效的组合。特别地,当ri=0时,则有
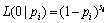 (4)
(4)
考虑到在利用贝叶斯统计方法处理数据时,不但要利用样本自身所包含的信息,而且还要利用由历史经验所得到的未知参数的先验信息。因此,使用Bayes方法的关键在于如何利用先验信息来确定先验分布。对于高速列车轴承试验的总体,其试验结果仅分为失效和未失效,符合成败型试验的总体,故选取二项分布的共轭分布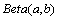 作为累积失效概率pi的先验分布[13]。
作为累积失效概率pi的先验分布[13]。
对于Beta分布,其在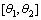 上的不完全Beta分布
上的不完全Beta分布 的密度函数为[14]:
的密度函数为[14]:

 <x<
<x<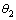 (5)
(5)
其中: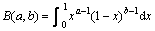 为Beta函数,a>0,b>0,
为Beta函数,a>0,b>0, <
<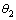 。
。
根据参数a和b可得Beta分布在[0,1]上的概率密度曲线如图1所示。
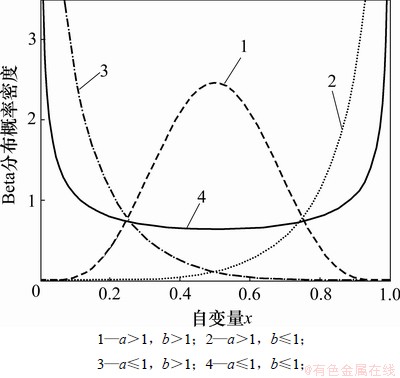
图1 Beta分布概率密度函数曲线
Fig.1 Probability density functional curve of Beta distribution
结合以往轴承的使用情况和试验分析,在[0, ti]时间内,由于试验样本无一失效,故轴承在此时间段内的失效概率pi一般会明显偏小。也就是说,如果pi在某个区间内取值,失效概率pi取值较大的可能性小,pi取值较小的可能性大。从图1可以看出:当a≤1,b>1时,Beta分布的概率密度函数是单调递减的,这符合各累积失效概率pi较大的可能性小,而pi较小的可能性大的先验信息。因此,为计算方便,不妨暂取a=1,b>1,但由于样本信息及其历史经验信息不足难以确定b,根据贝叶斯统计方法,在先验分布中所含的未知参数称为超参数,故在此取超参数b为服从(1,u)上的均匀分布。上限u可由专家经验给定,也可由无失效数据的有关信息给定。
2.2.1 累积失效概率p1的估计
取Beta(0,1,1,b)分布做为累积失效概率p1在区间(0,1)上的先验分布,在超参数b服从(1,u)上均匀分布的条件下,可得累积失效概率p1的多层先验分布为:
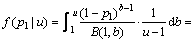
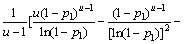
 (6)
(6)
由Bayes定理,p1的后验分布为:
 (7)
(7)
由于Bayes点估计是相对于所选损失函数风险最小的估计,而常用的损失函数为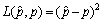 。
。 表示对参数p采取决策
表示对参数p采取决策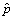 时所带来的损失。在该损失函数下,参数p的Bayes估计就是它的验后均值。因此,在平方损失下,以式(3)为似然函数、式(6)为先验分布的累积失效概率p1的Bayes估计为:
时所带来的损失。在该损失函数下,参数p的Bayes估计就是它的验后均值。因此,在平方损失下,以式(3)为似然函数、式(6)为先验分布的累积失效概率p1的Bayes估计为:
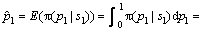
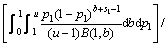
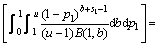

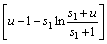 (8)
(8)
其中: 表示对
表示对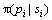 的数学期望,i=1, 2, …, k。
的数学期望,i=1, 2, …, k。
2.2.2 累积失效概率pi(i>1)的估计
由于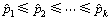 ,因此仍取超参数b为(1, u)上的均匀分布,取不完全Beta分布
,因此仍取超参数b为(1, u)上的均匀分布,取不完全Beta分布 作为累积失效概率p2在区间
作为累积失效概率p2在区间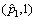 上的先验分布。于是,累积失效概率p2的多层先验分布为:
上的先验分布。于是,累积失效概率p2的多层先验分布为:
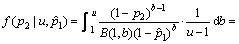
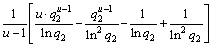 (9)
(9)
其中: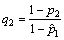 。
。
由Bayes定理,p2的后验分布则为:
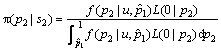 (10)
(10)
根据Bayes估计方法,计算得累积失效概率p2为:
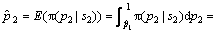
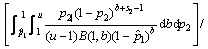

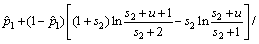
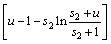 (11)
(11)
综合归纳可得,超参数b仍取为(1, u)上的均匀分布,不完全 分布为累积失效概率pi在区间
分布为累积失效概率pi在区间 上的先验分布,则累积失效概率pi的多层先验分布为:
上的先验分布,则累积失效概率pi的多层先验分布为:
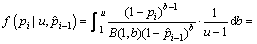
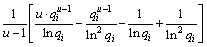 (12)
(12)
其中: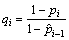 。
。
同理,pi的后验分布则为:
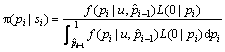 (13)
(13)
根据Bayes方法计算得累积失效概率pi的通用公式为:

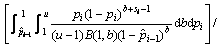
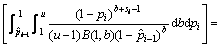
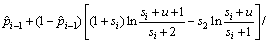
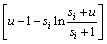 (i=1, 2, …, k) (14)
(i=1, 2, …, k) (14)
计算的累积失效概率 是对
是对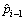 的改进,它的计算结果不仅和
的改进,它的计算结果不仅和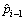 有关,而且还和样本n1,n2,…,ni及上限u有密切的联系,因此,此方法可以充分利用样本信息和历史经验信息,计算结果更加准确。
有关,而且还和样本n1,n2,…,ni及上限u有密切的联系,因此,此方法可以充分利用样本信息和历史经验信息,计算结果更加准确。
3 二参数Weibull分布的参数估计
在根据Bayes法得到各截尾时刻ti的累积失效概率pi的估计 后,利用最小二乘法来综合讨论二参数Weibull分布在无失效情况下的参数估计。
后,利用最小二乘法来综合讨论二参数Weibull分布在无失效情况下的参数估计。
由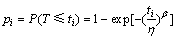 ,将计算的估计值
,将计算的估计值 取代各累积失效概率pi,利用加权最小二乘法进行参数拟合,取权重
取代各累积失效概率pi,利用加权最小二乘法进行参数拟合,取权重 ( i=1, 2, …, k),令
( i=1, 2, …, k),令
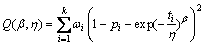 (15)
(15)
通过计算,使得(15)式取得最小值的 和
和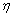 的点估计
的点估计 和
和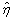 分别为:
分别为:
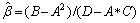 (16)
(16)
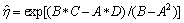 (17)
(17)
其中: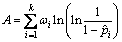 ,
, ,
,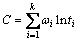 ,
,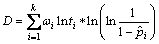 。
。
将形状参数 及尺度参数
及尺度参数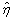 的计算值代入式(2),可得在任意时刻t的可靠度为:
的计算值代入式(2),可得在任意时刻t的可靠度为:
 (18)
(18)
4 仿真试验
针对高速列车拟采用的某改进型双列圆锥滚子轴承,随机选取其中2套为1组,进行10次定时截尾寿命仿真试验。其中轴承转速为2 063 r/min(即模拟列车时速为350 km/h)。根据列车行驶80万km的检修期要求,拟对轴承试验进行的最终截止时间为2 300 h。
由于高速列车轴承属高可靠性产品,故假定在试验过程中,第10次定时截尾结束后轴承试验时间已达2 300 h,但并未出现失效数据。因此,根据依次定时截尾试验时间得到无失效的仿真试验数据见表1。
表1 仿真试验数据
Table 1 Simulation testing data
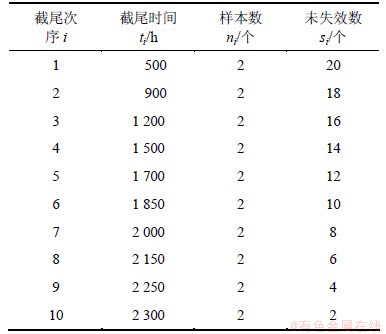
当处理轴承的仿真试验数据时,由于参数u的确定具有一定主观性,因此要求计算方法必须具有较好的稳健性[10],以保证在参数u发生扰动时,计算结果不会发生大的改变。根据项目的指标要求,列车运行到60万km(即列车轴承工作1 700 h)的故障率最大值应在[0.005,0.015]之间,结合仿真截尾试验数据,也即第5次截尾时的累积失效概率应不高于0.015。由式(6)~(14),可计算得第5次截尾时的累积失效概率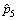 与上限参数u的关系(见图2)。
与上限参数u的关系(见图2)。
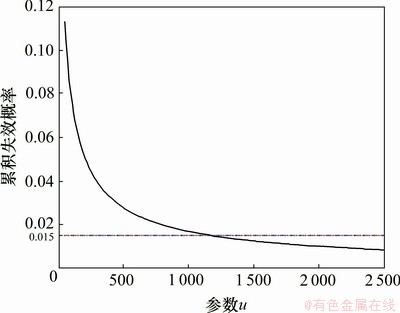
图2 累积失效概率 与参数u的关系
与参数u的关系
Fig.2 Relationship between cumulative failure probability  and parameter u
and parameter u
根据图2,参数u可在1 150~1 200之间取值。为说明u的选取对统计结果的影响,分别取u为1 150,1 175,1 200,1 225,1 250,1 275,1 300,1 325,将各截尾时刻的累积失效概率以及Weibull分布中的2个参数和可靠度的估计结果分别见表2和表3。
表2 各截尾时刻的累积失效概率估计值
Table 2 Accumulation failure probability estimated value in every chopped time 10-2
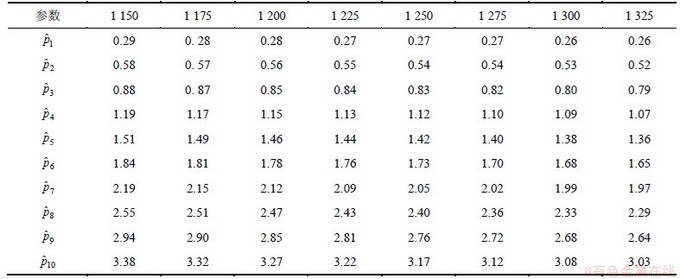
表3 Weibull分布中的参数和可靠度估计值
Table 3 Estimated value of parameter and reliability in Weibull distribution
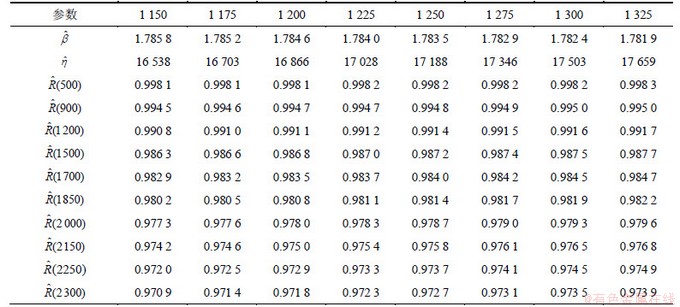
从表2和表3可以看出:参数u的变化对累积失效概率、Weibull分布中的2个参数 和
和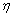 的估计,以及对轴承的可靠性指标的估计影响均不大,说明所采用的方法具有较好的稳健性。且轴承在工作到1 700 h时的可靠度估计也与先验信息较相符。如表2 所示,与第5次累积失效概率应不高于0.015的先验信息最接近的u为1 175,故确定超参数b的均匀分布上限u取值为1 175,则高速列车轴承在任意时刻的可靠度表达式为:
的估计,以及对轴承的可靠性指标的估计影响均不大,说明所采用的方法具有较好的稳健性。且轴承在工作到1 700 h时的可靠度估计也与先验信息较相符。如表2 所示,与第5次累积失效概率应不高于0.015的先验信息最接近的u为1 175,故确定超参数b的均匀分布上限u取值为1 175,则高速列车轴承在任意时刻的可靠度表达式为:
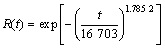 (19)
(19)
当可靠度为95%时,可计算得轴承的可靠性寿命为3 163.9 h。此时,列车所行驶里程为1.11×106 km。
由此可知,计算结果符合SKF对运营速度高于200 km/h的铁路轴承台架试验必须运转80万km当量里程,装车试验必须达到100万km的要求[15]。因此,如果高速列车轴承的可靠性试验中经过定时截尾试验(表1)后,样本无一失效,则可认为该双列圆锥滚子轴承的设计已基本达到使用寿命的要求。
5 结论
(1) 利用Bayes可靠性数据处理方法,得出极小样本零失效下的高速列车轴承可靠性数学模型,计算结果满足实际要求,从而为评估高速列车轴承的可靠性提供了一定的指导方法。
(2) 在利用Bayes方法的估计过程中,不仅包含了样本数据本身的信息,还加入了分布函数的特点,信息量增加了,评估结果也更加准确。
(3) 要保证在极少量的试验数据情况下能得到更准确和更加可信的可靠性评估结果,在今后的工作中还应多注意对先验信息的不断累积、收集和加工,使其数量化,形成先验分布,应用于Bayes统计推断中。
参考文献:
[1] 徐玉茗, 邓超, 吴军. 基于Bootstrap方法的可靠性评估[J]. 机械设计与制造, 2010, 3(3): 105-107.
XU Yuming, DENG Chao, WU Jun. An reliability assessment method based on bootstrap[J]. Machinery Design & Manufacture, 2010, 3(3): 105-107.
[2] 程皖民, 冯静, 周经伦, 等. Weibull分布航天产品可靠性评估的MMLE-Bayes方法[J]. 电讯技术, 2006, 46(6): 22-27.
CHENG Wanmin, FENG Jing, ZHOU Jinglun, et al. MMLE-Bayes reliability assessment method for aerospace products with Weibull distribution[J]. Telecommunication Engineering, 2006, 46(6): 22-27.
[3] 王景芹, 唐义良, 陆俭国. 小样本及无失效数据时电器产品可靠性特征量的估计[J]. 电工技术学院, 2000, 15(4): 27-31.
WANG Jingqin, TANG Yiliang, LU Jianguo. Estimation method of reliability characteristic parameter of electrical apparatus products for a few of failure data and zero-failure data[J]. Transactions of China Electrotechnical Society, 2000, 15(4): 27-31.
[4] 峁诗松, 王玲玲, 濮晓龙. 威布尔分布场合无失效数据的可靠性分析[J]. 应用概率统计, 1996, 12(1): 95-107.
MAO Shisong, WANG Lingling, PU Xiaolong. Reliability analysis for Weibull zero failure data[J]. Chinese Journal of Applied Probability and Statistics, 1996, 12(1): 95-107.
[5] 曹浪, 李银军, 李献锋, 等. 基于小样本Bayes理论的可靠性评估方法[J]. 电子质量, 2010, 10: 25-27.
CAO Lang, LI Yinjun, BAI Xianghua. Research on reliability evaluation method based on Bayes theory of small-sample[J]. Electronics Quality, 2010, 10: 25-27.
[6] Li D C, Chang F M., Chen K C. Building reliability growth model using sequential experiments and the Bayesian theorem for small datasets[J]. Expert Systems with Applications, 2010, 37 (4): 3434–3443.
[7] Thomas L, John S J H. Bayesian methods: An analysis for statisticians and interdisciplinary researchers[M]. Beijing: China Machine Press, 2005: 75-97.
[8] 武毅俊. 无失效数据场合失效概率的Bayes估计[J]. 龙岩学院学报, 2007, 25(3): 11-13.
WU Yijun. Bayes estimation of failure probability of zero-failure data[J]. Journal of Longyan University, 2007, 25(3): 11-13.
[9] 刘海涛, 张志华. 威布尔分布无失效数据的Bayes可靠性分析[J]. 系统工程理论与实践, 2008, 28(11): 103-108.
LIU Haitao, ZHANG Zhihua. Bayesian reliability analysis of Weibull zero failure data[J]. Systems Engineering Theory & Practice, 2008, 28(11): 103-108.
[10] 陈文华, 崔杰, 潘俊, 等. 威布尔分布下失效率的Bayes验证试验方法[J]. 机械工程学报, 2005, 41(12): 118-121.
CHEN Wenhua, CUI Jie, PAN Jun. Bayesian demonstration test method for failure rate under Weibull distribution[J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 118-121.
[11] LOU Hongliang, LI Xinglin, ZHUO Jizhi, et al. Reliability evaluation for rolling bearings with small sampling based on bayes method[C]//The 8th International Conference on Reliability, Maintainability and Safety. Chengdu: IEEE Press, 2009: 1112-1114.
[12] 楼洪梁, 徐现昭, 李兴林, 等. 滚动轴承寿命及可靠性试验评定方法研究[J]. 中国计量学院学报, 2011, 22(2): 124-127.
LOU Hongliang, XU Xianzhao, LI Xinglin, et al. Study on a life and reliability test evaluation methods of rolling bearings under small sample[J]. Journal of China University of Metrology, 2011, 22(2): 124-127.
[13] 赵宇. 可靠性数据分析[M]. 北京: 国防工业出版社, 2011: 251-266.
ZHAO Yu. Data analysis of reliability[M]. Beijing: National Defense Industry Press, 2011: 251-266.
[14] 张继昌. 无失效数据的Bayes分析[J]. 高校应用数学学报, 1995, 10(1): 19-25.
ZHANG Jichang. Bayesian analysis of the zero-failure data[J]. Applied Mathematics: A Journal of Chinese Universities, 1995, 10(1): 19-25.
[15] 杨晓蔚. 高速铁路轴承概述[J]. 轴承, 2011(10): 59-61.
YANG Xiaowei. Overview of high speed rail bearings[J]. Bearings, 2011(10): 59-61.
(编辑 赵俊)
收稿日期:2012-04-02;修回日期:2012-07-20
基金项目:国家科技支撑计划项目(2011BAF09B01);陕西省自然科学基金资助项目(2012JQ7011)
通信作者:朱德馨(1981-),男,河南驻马店人,博士研究生,从事可靠性试验研究;电话:15877659577;E-mail: zdx_cn@163.com