
J. Cent. South Univ. (2020) 27: 2280-2290
DOI: https://doi.org/10.1007/s11771-020-4449-0
Influence of support stiffness on vibrations of a planet gear system considering ring with flexible support
LIU Jing(刘静)1, 2, PANG Rui-kun(庞瑞琨)2, LI Hong-wu(李洪武)3, XU Jin(许晋)3
1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China;
3. China North Vehicle Research Institute, Beijing 100081, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Planet gear systems (PGSs) are key components of transmission mechanisms. Structural and material characteristics of gearbox and shaft can affect the support stiffness and vibrations of PGSs. The ring gear flexibility should affect the vibrations of PGSs too. However, most previous work did not completely consider the effects of the ring gear flexibility on the vibrations of PGSs and flexible supports of ring and sun gears. Thus, this paper presents a flexible-rigid coupling multi-body dynamic (FMBD) model for a PGS with the flexible supports and ring gear flexibility. A finite element model of ring gear is established to formulate the ring gear flexibility. The influences of clearance and damping of planet bearings on the vibrations of PGS are considered. The effects of flexible supports and ring gear flexibility on the vibrations of PGS under different moment and speed conditions are studied. The statistical parameters and peak frequencies of PGS from the proposed FMBD and previous rigid multi-body dynamic (RMBD) models are compared. The results denote that the flexible support has a great effect on the vibrations of PGS. This paper can provide some guidance for the support structure design and vibration control for PGSs.
Key words: planet gear; flexible-rigid coupling; flexible supports; ring gear flexibility; vibrations
Cite this article as: LIU Jing, PANG Rui-kun, LI Hong-wu, XU Jin. Influence of support stiffness on vibrations of a planet gear system considering ring with flexible support [J]. Journal of Central South University, 2020, 27(8): 2280-2290. DOI: https://doi.org/10.1007/s11771-020-4449-0.
1 Introduction
Planet gear systems (PGSs) are widely used in various mechanical equipment. The PGSs have high transmission ratio and high transmission efficiency. A large vibration in the PGSs may cause different failures including cracks and pits in the gears and bearings [1-3]. Therefore, vibration studies of PGSs should be necessary. The supports of PGSs may greatly affect the vibrations of PGSs. It is of great significance to understand the effect of the supports on the vibrations of PGSs.
In previous works, various methods including the centralized parameter method, finite element (FE), rigid multi-body dynamic (RMBD), and experimental methods were presented to study the vibrations of PGSs [4, 5]. LIU et al [6] established a dynamic model to analyze the vibrations of a pitting gear system. THORET-BAUCHET et al [7] established a model of a PGS to analyze the influence of a pitting on the dynamic behaviours of the PGS. WANG et al [8, 9] formulated a generalized dynamic model of gear driveline system to understand the interaction between the hypoid gear pair and propeller shaft. LIN et al [10] proposed a FMBD model considering the ring gear flexible deformation to study the effect of gyro response on the vibrations of a PGS. KAHRAMAN et al [11] established a torsion model of PGS and proposed a calculation method of natural frequency for analyzing the inherent characteristic of a PGS. YU et al [12] established a new dynamic model of a cylindrical gear pair with localized spalling defects to assessment the effects of tooth defects on the vibration response of a PGS. GUO et al [13] developed a centralized parameter model with the bearing clearance, backside contact, pitch and width of the gear to analyze the vibrations of a PGS. XIAO et al [14] established a torsion dynamic model to analyze the vibrations of a PGS. BODAS et al [15] studied the effects of manufacturing errors of carrier and gear on the static uneven load coefficient of a PGS by using a FE model. LIU et al [16] established a dynamic model with a locally imperfection rigid rotor bearing system considering additional edge deformation. XUE et al [17] studied the effect of the flexible ring gear on the vibrations of a PGS by using FE method.
Most previous researches only studied the effects of single rigid ring gear, rigid planet gear or planet bearing on the vibrations of PGSs. Some studied a ring gear flexibility FE model with rigid support [18]. LI et al [19] studied an RMBD model with flexible support without considering ring gear flexibility. In practice, both the ring gear flexibility and flexible support have great effect on the vibrations of PGSs, which cannot be ignored. Thus, this paper presents a flexible-rigid coupling multi-body dynamic (FMBD) model for a PGS with the flexible supports and ring gear flexibility. A finite element model of the ring gear is established to formulate the ring gear flexibility. The Hertzian theory is used to calculate the meshing stiffness and damping of gears. The effects of flexible supports and ring gear flexibility on the vibrations of PGS are studied under different load and input speed conditions. The statistical parameters and peak frequencies of PGS from the proposed FMBD and previous rigid multi-body dynamic (RMBD) models are compared. The results denote that the flexible support has a great effect on the time- and frequency-domain vibrations of PGS. This paper can provide some guidance for the support structure design and vibration control for PGSs.
2 Problem description
The meshing forces and radial loads can cause the flexible deformation of the ring gear during the working conditions of the PGS, which cannot be described by the RMBD model. The flexible deformation of the ring gear can produce the unacceptable vibrations and imbalance of the PGS. The finite element method is used to calculate the flexibility of the ring gear. The finite element model of the ring gear is developed by using a commercial software ANSYS. The dynamic model of the PGS is established by a commercial software ADAMS.
Figure 1 shows a FMBD model of a PGS with the ring gear flexibility and flexible support of sun and ring gears. The model has three planet bearings. The bearings are used to connect the planet gears and the carrier; the outer of bearings are linked to the planet gears while the inner of bearings are linked to the carrier. The planet gears are simplified to the internal mesh stiffness between the bearing and the outer ring. According to the research [20], the flexible support of ring gear affects the vibration of PGS. The flexible support of the ring can be determined by the support stiffness and number of the support positions between the ring gear and the gearbox. In practice, the sun gear floats in the radial direction; and its displacement is limited by the radial flexible support. The flexible supports of ring and sun gears are considered in this paper, where Kr1 and Kr2 are the support stiffness of ring and sun gears respectively.
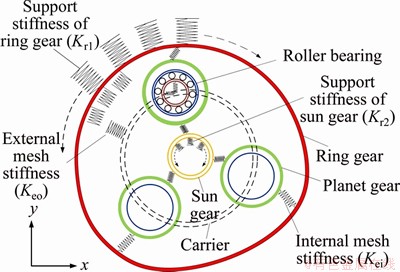
Figure 1 Schematics of a PGS with ring gear flexibility and flexible supports
Here, Kr1 and Kr2 distribute from 1×106 N/mm to 5×106 N/mm. The FMBD and RMBD models with different Kr1 and Kr2 are simulated under different input speeds (nin) and moments (Mp). The input speed and moment are applied on the sun gear and carrier, respectively. The time-domain and frequency-domain results are analyzed. Table 1 shows nin and Mp in this paper.
Table 1 Simulation conditions of ring and sun gears

3 Model formulation
The FMBD model for a PGS is depicted in Figure 1. The FMBD model includes a sun gear with the flexible support, a ring gear flexibility with the flexible support, a carrier, three planet gears and three IBC NU202 planet bearings. The dynamic performance and rotational accuracy of the PGS can be greatly affected by the bearing clearance. Therefore, the bearing clearance is defined as 20 μm. The geometric parameters of the components are listed in Tables 2 and 3.
According to the potential energy principle, the meshing stiffness between the ring and planet gears (Keo) is calculated by [21-23]:
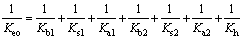 (1)
(1)
where Kb, Ks, Ka and Kh are the bending, shear, axial compressive, and Hertz contact stiffness, respectively. In Eq. (1), the subscripts 1 and 2 denote the sun and planet gears, respectively. The meshing stiffness between the planet and sun gears (Kei) is calculated by [16-18]:
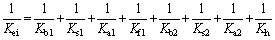 (2)
(2)
where Kf is the fillet-foundation stiffness. In Eq. (2), the subscripts 1 and 2 represent the planet and ring gears, respectively. The details in Eqs. (2) and (3) are given in CHEN et al [24], TIAN [21], and MA et al [25, 26]. In Eqs. (1) and (2), Kb, Ks, Ka and Kh are calculated by:
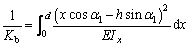 (3)
(3)
 (4)
(4)
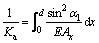 (5)
(5)
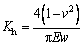 (6)
(6)
where h is the distance between the mesh point and gear midline; x is the distance between the mesh point and a region of width of dx on the gear; α1 is the defunct angle of contact force; d is the distance between the mesh point and root of gear; E and G are the elastic and shear modulus, respectively; Ix and Ax are the area moment of inertia and the area of section at a distance of x between the mesh point and the section, respectively.
The contact damping of the gears (cmax) is calculated by [27]:
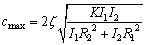 (7)
(7)
where ζ is 0.1; K is the meshing stiffness; I1 and I2 are the rotational inertias of meshing gears, respectively; R1 and R2 are the radii of two gears, respectively.
The contact stiffness (Kbr) between the rollers and bearing race is [28, 29]:
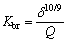 (8)
(8)
where δ is expressed as:
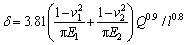 (9)
(9)
Table 2 Geometric parameters of gears

Table 3 Geometric parameters of planet bearings
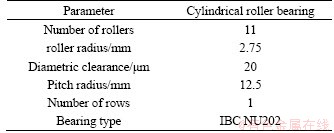
where E1 and E2 are the elastic modulus; v1 and v2 are Poisson ratios; Q is the load; l is the equivalent contact length of roller. Furthermore, the contact damping of bearing is given as:
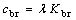 (10)
(10)
where λ is from 0.25 to 2.5×10-5 [30, 31].
Moreover, the governing equation of the FMBD model is represented by:
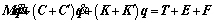 (11)
(11)
where M is the mass; K and K′ are the flexible support matrice and contect stiffness matrice for PGS, respectively; C and C′ are the support damping matrice and contect damping matrice for PGS, respectively; q is the vector of generalized displacement for PGSs; T, E and F are the external system load vector, fault excitation vector and internal system vector, respectively. Moreover, F also includes the friction force. The meshing stiffness and damping between sun and planet gears are 4.71×105 N/mm and 86.62 N·s/mm, respectively. The meshing stiffness and damping between ring and planet gears are 9.28×105 N/mm and 157.59 N·s/mm, respectively. The contact stiffness and damping between the roller and bearing race are 4.35×105 N/mm and 8.7 N·s/mm, respectively.
4 Results and discussion
The commercial software MSC. Adams (for developing the FMBD model and solving the results) and ANSYS (for developing FE model of ring gear) are used in this paper to study the influence of the support stiffness on the RMBD and FMBD models. The FE model of ring gear is meshed by using the tetrahedron elements as shown in Figure 2. The element length is defined as 1 mm. The material model of the ring gear is defined as a linear elastic one.
To limit that the radial deformations dr1 and dr2 of the ring and sun gears are less than 1 mm, the flexible support Kr in the FMBD and RMBD models is assumed to be from 1×106 N/mm to 5×106 N/mm in the studied conditions. The support stiffness of ring and sun gears are calculated by:
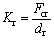 (12)
(12)
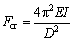 (13)
(13)
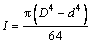 (14)
(14)
when Fcr is the critical force; D and d are the outside and inside diameters of ring and sun gear, respectively; I is the moment of inertia.

Figure 2 Flexible ring gear meshed by using tetrahedron elements
The effects of flexible supports on the vibration of PGS are discussed. The results of FMBD and RMBD models are compared to analyze the effect of ring gear flexibility on the vibrations of PGS.
4.1 Model validation
To ensure the accuracy of results, the correctness of FMBD model is validated. The simulation and theoretical angular velocities are compared when nin is 1000 r/min (6000°/s). The time-domain simulation results are shown in Figure 3. The planet gears and carrier’s angular velocity are 1780°/s and 1116°/s. Although the angular velocity fluctuates due to the bearing clearance, gear backlash, or elastic deformations, it is relatively stable one. The simulation results are basically consistent with the theoretical results, which can validate the FMBD model.
4.2 Effects of flexible supports on time-domain vibration
The radial acceleration of ring gear is used to describe the vibrations of PGS here. To analyze the effect of the ring gear flexibility on the time-domain vibration, three statistic parameters of the radial acceleration of ring gear, such as the maximum (MAX), peak to peak (PTP) and root mean square (RMS), are introduced. The simulation results of FMBD and RMBD models are analyzed. The values used in the studied flexible support cases are defined by the practical work conditions of the PGS. Figures 4 to 8 describe the effects of the flexible supports (Kr1 and Kr2) on the MAX, PTP and RMS. The MAX, PTP and RMS increase with nin. nin is 3500 r/min; and Mp values are 500, 1000 and 1500 N·m in Figures 9 to 10. In Figures 4 to 8, the RMS, MAX, and PTP distributions are similar for different simulation conditions; the RMS decreases with the increment of Kr2; the effect of Kr1 on the RMS is small. The maximum values of MAX and PTP are observed when Kr1 is about 4×106 N/mm and Kr2 is from 2×106 N/mm to 4×106 N/mm. The distributions of RMS, MAX and PTP for the FMBD and RMBD models are also similar. But, the RMS, MAX, and PTP values of FMBD model are much larger than those of RMBD model. The time-domain results indicate that the vibrations of PGS are affected by both Kr1 and Kr2. The effect of Kr2 is bigger than that of Kr1. The vibration of FMBD model is larger than that of RMBD model under the same nin and Mp. Thus, the ring gear flexibility should be considered in the dynamic modeling of PGS.
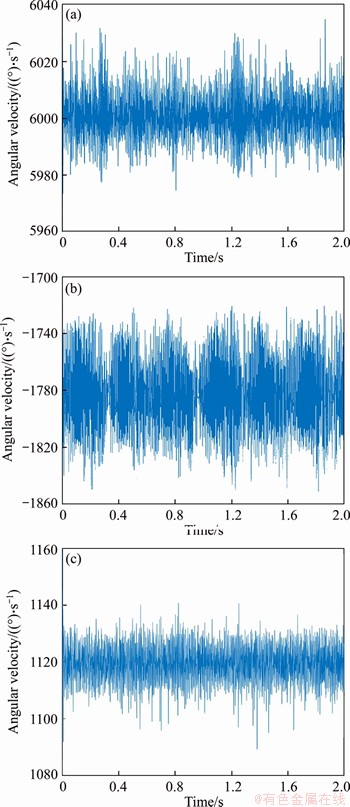
Figure 3 Simulation angular velocity of sun gear (a), planet gear (b), and carrier (c)
4.3 Effects of flexible supports on frequency- domain vibrations
To analyze the effects of flexible supports and ring gear flexibility on the frequency-domain vibrations, the frequency of radial acceleration of ring gear is used here.
The simulation results of FMBD and RMBD models are analyzed. Figures 9 and 10 describe the effects of flexible supports (Kr1 and Kr2) on the frequencies of PGS. Table 5 shows the peak frequencies (The frequency corresponding to the peak value in the spectrum diagram) of FMBD and RMBD models with different flexible support cases when nin=3000 r/min, Mp=500 N·m. In Figure 9, Kr2 is 1×106 N/mm, and Kr1 is 1×106 N/mm, 2×106 N/mm, 3×106 N/mm, 4×106 N/mm, and 5×106 N/mm. Two peak frequencies fm-fs=723 Hz and 2fm-2fs-2fc=1417 Hz of FMBD and RMBD models are observed. In Figure 10, Kr1 is 1×106, Kr2 is 1×106, 2×106, 3×106, 4×106 and 5×106 N/mm, the same peak frequencies fm-fs=723 Hz and 2fm-2fs- 2fc=1417 Hz of FMBD and RMBD models are observed. Here, fm is the meshing frequency of ring and planet gears; fs is the rotational frequency of sun gear; and fc is the rotational frequency of carrier [32, 33]. The relative spectra are similar for different flexible support cases. The maximum values of peak frequencies fm-fp and 2fm-2fs-2fc are observed when Kr1=1×106 N/mm and Kr2=2×106 N/mm or Kr2=1×106 N/mm and Kr1=2×106 N/mm. The peak frequency amplitudes decrease with the increment of Kr1 and Kr2. The effect of Kr1 on the peak frequency is small. The spectrum waves of FMBD and RMBD models are similar. But the peak frequency amplitudes of FMBD model are much larger than those of RMBD model. The frequency-domain results indicate that the vibrations of PGS are affected by both Kr1 and Kr2. The effect of Kr2 is bigger than that of Kr1. The vibrations of FMBD model are larger than those of RMBD model under the same nin and Mp. Thus, the ring gear flexibility should be considered in the dynamic modeling of PGS.
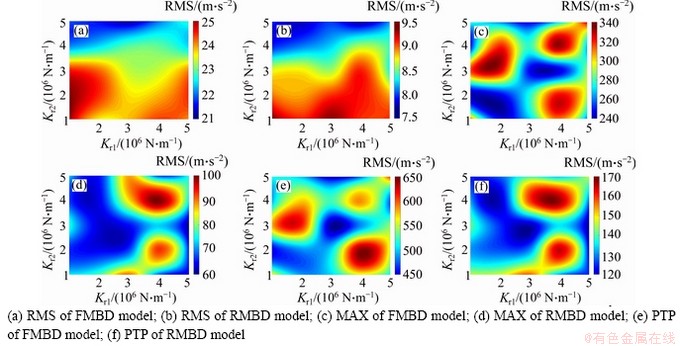
Figure 4 Effects of flexible supports (Kr1 and Kr2)on time-domain vibrations when nin=2500 r/min and Mp=500 N·m:
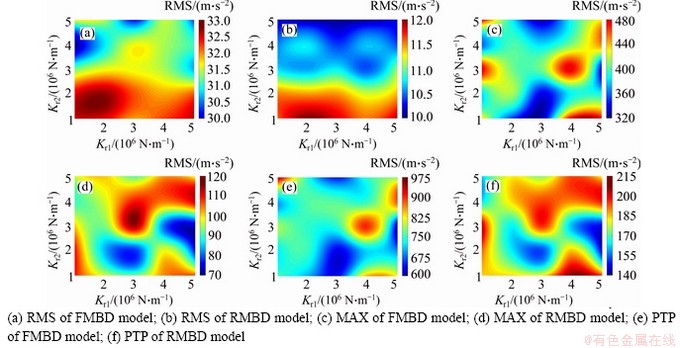
Figure 5 Effects of flexible supports on time-domain vibration when nin=3000 r/min and Mp=500 N·m:
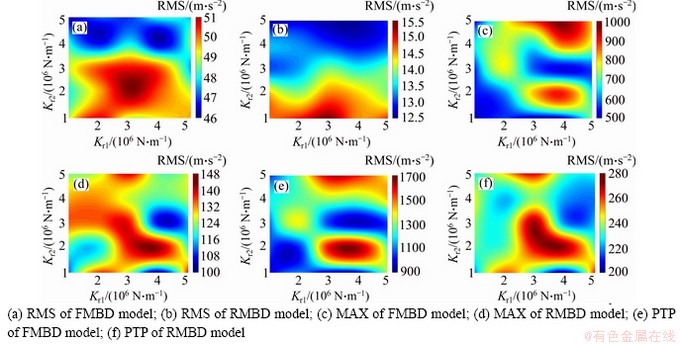
Figure 6 Effects of flexible supports on time-domain vibration when nin=3500 r/min and Mp=500 N·m:
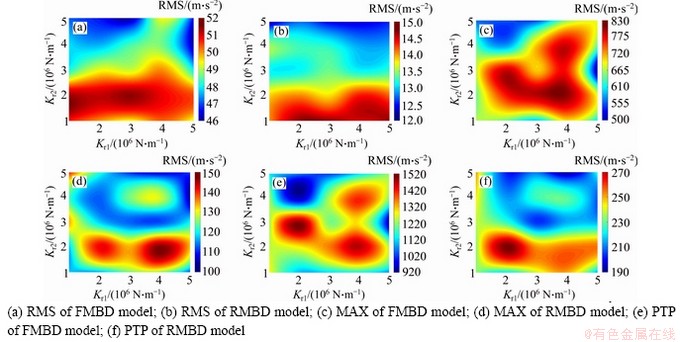
Figure 7 Effects of flexible supports on time-domain vibration when nin=3500 r/min and Mp=1000 N·m:
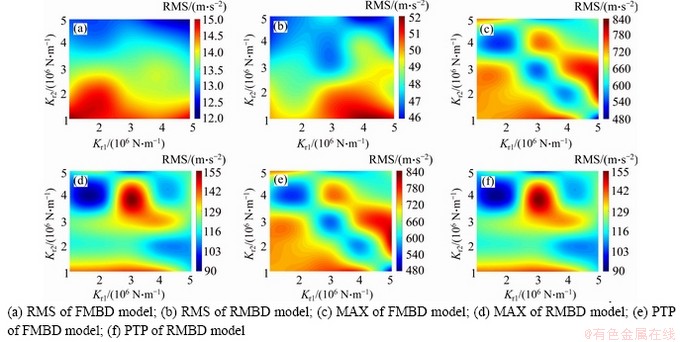
Figure 8 Effects of flexible supports on time-domain vibration when nin=3500 r/min and Mp=1500 N·m:
5 Conclusions
In this paper, a FMBD model of PGS with the flexible supports of ring and sun gears is established. The effects of the ring gear flexibility and flexible supports on the vibrations of PGS are discussed. The analysis results may give a new method to decrease the vibrations and improve the quality of PGSs. The conclusions are as follows.
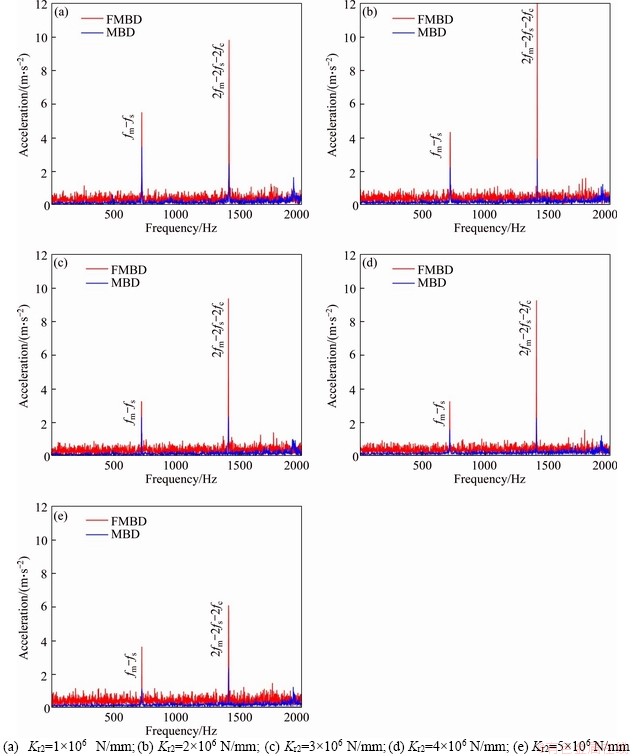
Figure 9 Effect of flexible support of ring gear (Kr2) on frequency-domain vibrations when nin=3000 r/min, Mp=500 N·m, and Kr1=1×106 N/mm:
Table 4 Characteristic frequencies of PGS when nin=3000 r/min

1) The flexible supports of sun and ring gears can affect the vibrations of PGSs. In general, the vibration magnitude of PGS decreases with the increment of the flexible supports. The effect of the flexible support of ring gear is bigger than that of sun gear. The results show that the effect of the input speed on the vibrations of PGS is bigger than that of the moment.
2) The ring gear flexibility can affect the vibrations of PGS too. The FMBD model’s statistic parameters, such as RMS, MAX, and PTP, are bigger than those of RMBD model. The magnitude of the vibrations from FMBD model is larger than that from RMBD model according to the RMS. The effects of the flexible supports on the vibration waveforms from FMBD and RMBD models are similar.
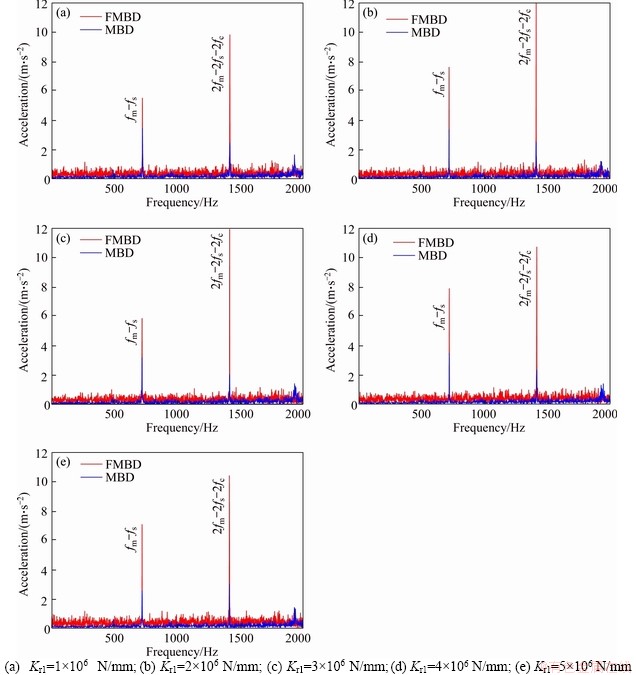
Figure 10 Effect of flexible support of sun gear (Kr1) on frequency-domain vibrations when nin=3000 r/min, Mp=500 N·m, and Kr2=1×106 N/mm:
Table 5 Peak frequencies of FMBD and RMBD models with different flexible support cases when nin=3000 r/min, Mp=500 N·m
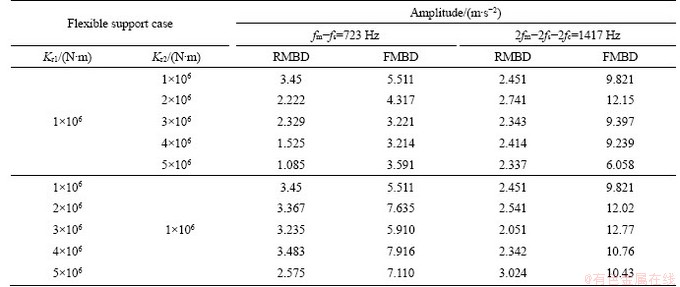
3) The FMBD and RMBD models have the same peak frequencies fm-fs and 2fm-2fs-2fc. The amplitude of peak frequency in the spectrum is affected by the flexible supports. The changes of peak frequencies for the FMBD and RMBD models caused by different flexible support cases are similar. The FMBD model’s peak frequency amplitude is bigger than that of RMBD model.
In the current study, the simulation results show that FMBD and RMBD models have a big difference on time-domain and frequency-domain vibrations. The purpose of this paper is to study the influence factors-support stiffness and flexible deformation of ring gear. The confirmatory experiment will be done in in the future study.
References
[1] CHEN Z, ZHU Z, SHAO Y. Fault feature analysis of planet gear system with tooth root crack and flexible ring gear rim [J]. Engineering Failure Analysis, 2015, 49: 92-103. DOI: https://doi.org/10.1016/j.engfailanal.2014.12.014.
[2] LIU J, XU Z, ZHOU L, YU W, SHAO Y. A statistical feature investigation of the spalling propagation assessment for a ball bearing [J]. Mechanism and Machine Theory, 2019, 131: 336-350. DOI: 10.1007/s11071-018-4314-y.
[3] LIU J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone [J]. Journal of Sound and Vibration, 2020, 469: 115144. DOI: https://doi.org/10.1016/ j.jsv.2019.115144.
[4] LIANG X, ZUO M J, FENG Z P. Dynamic modeling of gearbox faults: A review [J]. Mechanical Systems and Signal Processing, 2018, 98: 852-876. DOI: https://doi.org/10. 1016/j. ymssp.2017.05.024.
[5] MA H, ZENG J, FENG R, PANG X, WANG Q, WEN B. Review on dynamics of cracked gear systems [J]. Engineering Failure Analysis, 2015, 55: 224-245. DOI: https://doi.org/10.1016/j.engfailanal. 2015.06.004.
[6] LIU J, WANG C, WU W. Research on meshing stiffness and vibration response of pitting fault gears with different degrees [J]. Journal of Multi-body Dynamics, 2019, 233(3): 677-695. DOI: https://doi.org/10.1155/2020/417 6430.
[7] THORET-BAUCHET Q, VELEX P, GUINGAND M, CASANDVA P. Simulations of the dynamic response of planetary gears in the presence of localised tooth faults [J]. Journal of Mechanical Engineering Science, 2019, 233(21, 22): 7212-7223. DOI: https://doi.org/10.1177/0954406219 8461 53.
[8] WANG Y, YANG J, GUO D, KIM T C. Vibration and sound radiation analysis of the final drive assembly considering the gear-shaft coupling dynamics [J]. Journal of Mechincal Engineering Science, 2016, 230(7, 8): 1258-1275. DOI: https://doi.org/10.1177/0954406216632021.
[9] WANG Y, LI X, QIAO G, KIM T C. Effect of component flexibility on axle system dynamics [J]. SAE International, 2017, 1(2): 400-406. DOI: https://doi.org/10.4271/2017-01- 1772.
[10] LIN J, PARKER R. Analytical characterizationn of the unique properties of planet gear free vibration [J]. Journal of Vibration and Acoustics, 1999, 121(3): 316-321. DOI: https://doi.org/10.1115/1.2893982.
[11] KAHRAMAN A, KHARAZI A, UMRANI M. A deformable body dynamic analysis of planet gears with thin rims [J]. Journal of Sound and Vibration, 2003, 262: 752-768. DOI: 10.1016/S0022-460X(03)00122-6.
[12] YU W, MECHEFSKE C K, TIMUSK M. A new dynamic model of a cylindrical gear pair with localized spalling defects [J]. Nonlinear Dynamics, 2018, 9: 2077-2095. DOI: https://doi.org/10.1007/s11071-017-4003-2.
[13] GUO Y, PARKER R G. Dynamic modeling and analysis of a spur planet gear involving tooth wedging and bearing clearance nonlinearity [J]. European Journal of Mechanics-A, 2010, 29: 1022-1033. DOI: https://doi.org/10. 1016/ j.euromechsol.2010.05.001.
[14] XIAO Z, QIN D, WANG J. A torsional-dynamics of three-stage planet transmission system for the main reducer of shield machine [J]. China Mechanical Engineering, 2010, 21(18): 2176-2182.
[15] BODAS A, KAHRAMAN A. Influence of carrier and gear manufacturing errors on the static load sharing behavior of planet gear sets [J]. JSME International Journal Series, 2004, 47(3): 908-915. DOI: https://doi.org/10.1299/jsmec.47.908.
[16] LIU J, SHAO Y. Dynamic modeling for rigid rotor bearing systems with a localized defect considering additional deformations at the sharp edges [J]. Journal of Sound and Vibration, 2017, 398: 84-102. DOI: https://doi.org/10.1016/ j.jsv.2017.03.007.
[17] XUE S, HOWARD I. Vibration response from the planet gear with flexible ring gear [J]. International Journal of Powertrains, 2019, 8(1): 3-22. DOI: 10.1504/IJPT.2019. 098108.
[18] LIU J, XU Y, SHAO Y, XIAO Y, LI H. The effect of a localized fault in the planet bearing on vibrations of a planet gear set [J]. Journal of Strain Analysis for Engineering Design, 2018, 53(5): 313-323. DOI: https://doi.org/ 10.1177/030932471 8769491.
[19] LI H, LIU J, MA J, SHAO Y. Effect of the radial support stiffness of the ring gear on the vibrations for a planet gear system [J]. Journal of Low Frequency Noise, Vibration and Active Control, 2019. DOI: https://doi.org/10.1177/ 1461348419 844642.
[20] WU X, PARKER R G. Vibration of rings on a general elastic foundation [J]. Journal of Sound and Vibration, 2006, 295: 194-213. DOI: https://doi.org/10.1016/j.jsv.2006.01.007.
[21] TIAN X H. Dynamic simulation for system response of gearbox including localized gear faults [D]. Alberta, Canada: Edmonton: University of Alberta, 2004.
[22] CHEN Z, SHAO Y, SU D. Dynamic simulation of planet gear set with flexible spur ring gear [J]. Journal of Sound and Vibration, 2013, 332: 7191-7204. DOI: https://doi.org/ 10.1016/j.jsv.2013.07.026.
[23] CHEN Z, SHAO Y. Mesh stiffness of an internal spur gear pair with ring gear rim deformation [J]. Mechanism and Machine Theory, 2013, 69: 1-12. DOI: https://doi.org/ 10.1016/j.mechmachtheory.2013.04.017.
[24] CHEN Z, SHAO Y. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth [J]. Engineering Failure Analysis, 2011, 18: 2149-2164. DOI: https://doi.org/10.1016/j.engfailanal.2011. 07.006.
[25] MA H, PANG X, FENG R, FENG R, SONG R, WEN B. Fault features analysis of cracked gear considering the effects of the extended tooth contact [J]. Engineering Failure Analysis, 2015, 48: 105-120. DOI: https://doi.org/ 10.1016/j.engfailanal.2014.11.018.
[26] MA H, SONG R, PANG X, WEN B. Time-varying mesh stiffness calculation of cracked spur gears [J]. Engineering Failure Analysis, 2014, 44: 179-194. DOI: https://doi. org/10.1016/j.engfailanal.2014.05.018.
[27] AMABILI M, RIVOLA A. Dynamic analysis of spur gear pairs: Steady-state response and stability of the SDOF model with time varying meshing damping [J]. Mechanical Systems and Signal Processing, 1997, 11: 375-390. DOI: https:// doi.org/10.1006/mssp.1996.0072.
[28] ZHOU J. Dynamic model and simulation on typical fault of cylindrical roller bearing MS [D]. Chongqing, China: Chongqing University, 2012. (in Chinese)
[29] OKAMOTO J. Design and calculation of ball bearing [M]. Beijing: China Machine Press, 2003.
[30] LIU J, SHAO Y. An improved analytical model for a lubricated roller bearing including a localized defect with different edge shapes [J]. Journal of Vibration and Control, 2018, 24: 3894-3907. DOI: https://doi.org/10.1177/ 1077546317716315.
[31] LIU J, TANG C K, WU H, XU Z D, WANG L F, SHAO Y M. An analytical calculation method of the load distribution and stiffness of a preloaded angular contact ball bearing [J]. Mechanism and Machine Theory, 2019, 142: 103597. DOI: https://doi.org/10.1016/j.mechmachtheory.2019.103597.
[32] FENG Z, ZHU F, ZUO M. Fault diagnosis method of planet gear box [M]. Beijing: Science Press, 2015. DOI: https://doi.org/10.1007/978-3-319-62274-3_6.
[33] JAIN S. Skidding and fault detection in the bearings of wind-turbine gearboxes [D]. Cambridge: University of Cambridge, 2013.
(Edited by YANG Hua)
中文导读
柔性齿圈支承刚度对行星齿轮系统振动特性的影响规律
摘要:行星齿轮系统是传动机构的关键部件之一。齿轮箱和传动轴的结构和材料特性会影响行星齿轮系统的支承刚度和振动特性。齿圈的柔性也会影响行星轮系的振动特性。然而,当前的研究大多没有同时考虑齿圈的柔性以及齿圈和太阳轮支承刚度对行星轮系振动特性的影响规律。本文建立了考虑弹性支承的柔性齿圈行星齿轮系统的刚柔耦合多体动力学模型。采用有限元方法,计算获得了齿圈的柔性变形。此外,该模型还考虑了轴承游隙及阻尼对行星齿轮系统振动特性的影响。研究了不同力矩和转速工况下弹性支承和齿圈的柔性对行星齿轮系统振动特性的影响规律。对所提出的刚柔耦合模型和已有的刚性多体动力学模型的获得的计算结果进行了对比分析。结果表明,弹性支承的柔性齿圈对行星齿轮系统的振动特性影响较大。本文的研究成果对行星齿轮系统支承结构的设计和振动控制具有一定的指导意义。
关键词:行星轮;刚柔耦合;弹性支承;齿圈柔性;振动特性
Foundation item: Projects(51605051, 51975068) supported by the National Natural Science Foundation of China
Received date: 2020-03-05; Accepted date: 2020-05-22
Corresponding author: LIU Jing, PhD, Professor; Tel: +86-13658335960; E-mail: jliu@cqu.edu.cn; ORCID: https://orcid.org/0000- 0003-2323-3475