
Polycrystalline model for FE-simulation of micro forming processes
WANG Chun-ju, GUO Bin, SHAN De-bin
School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
Received 8 June 2010; accepted 6 December 2010
Abstract: A new polycrystal model was presented from the viewpoint of polycrystal structure of the billets considering free surface effects. In the model, the billet was divided into three portions, such as free surface portion, transition portion and internal portion. The grains in free surface portion were considered the single grains, and the anisotropy of the grains was taken into account by introducing grain orientation to explain the inhomogeneous deformation. In the transition portion, the effects of the neighbouring grains were adopted in the model. The grains in the internal portion were considered the polycrystalline material. With the developed model, the upsetting deformation process was simulated by the MSC Superform software. The scatter of the flow stress and inhomogeneous deformation was observed by analysis of the model. The comparisons show that the computational results are good agreed with the experimental results. This means that the presented model is effective.
Key words: micro forming; size effect; polycrystal model; inhomogeneous deformation
1 Introduction
From the viewpoint of production engineering, micro forming is an effective process to fabricate various micro parts for micro electro mechanical systems (MEMS). Since the microstructure and surface roughness of the specimens keep constant during miniaturization of the parts, size effects occur in micro forming processes. The classical plastic theories are yet not enough to explain the phenomena, so lots of investigations on micro forming processes have been carried out in recent years [1-2]. The size dependence of the flow stress on the billet dimensions have been identified by several micro forming processes [3-6]. When the size of the components decreases to the same order of the magnitude as the grain size, individual grains dominate the deformation of the billets. This leads to the decreasing of the dimensional accuracy and mechanical property homogeneity of the formed micro parts. The investigations have been done in Refs. [7-8] using bending tests, and micro combined extrusion tests respectively.
Since the metal forming technology for the production of micro parts was characterized by an empirical processes design, a new simulation method in thin sheet metal forming has been tried in Ref. [9] by introducing a size factor based on the investigations of size effects using the tensile and hydraulic bulging tests. Based on the polycrystal structure of billets, ENGEL et al [10] presented a FE-simulation model by dividing the billets into two parts, the surface portion and the internal portion. To describe the material behaviour in a more detail way, a mesoscopic model has been developed by considering the effects of the size and location of the grains based on the metal physics [11-12]. From the polycrystal materials, a finite element model of grain and grain boundary elements was developed [13]. However, the effect of single grain orientation is not considered, and the anisotropy of the grains and the strain hardening are neglected in the model.
The purpose of this work is to present a polycrystal model to investigate the micro forming processes from the viewpoint of polycrystal structure considering the surface effects and the deformation compatibility. The effects of the anisotropy of the grains and the strain hardening were taken into account in the model by considering the effect of single grain orientation.
2 Foundation of model
2.1 Theoretical backgrounds
With the decrease of the dimensions, size effects occur in micro forming processes. The dependence of the flow stress on the specimen size cannot be analyzed with the traditional theories applying the similarity theorem. So it is necessary to present a new model by analyzing the deformation mechanism. With the miniaturization of billets, the material is neither homogeneous nor isotopic and should be considered from the viewpoint of polycrystalline structure. Because of dislocation accumulation, the flow stress of the grains in the free surface layer is less than that of the internal grains of the billet because the dislocation segments near the free boundaries tend to move towards the boundary and annihilate [14]. On the other hand, the deformation incompatibility can lead to a higher flow stress in the polycrystalline material deformation because the number of acting slip systems is much larger than that in the single grain deformation [15]. Concerning the effects of the two factors mentioned above, the grains in the free surface layer are able to deform at a lower flow stress compared with internal grains in the polycrystalline material, and the deformation compatibility is easily realized. With a constant grain size, the number ratio of the grains in the free surface layer to the total grains becomes larger with the decrease of the dimension, which leads to the size dependence of the flow stress.
When the specimen dimensions scale down to the same order of the magnitude as the grain size, the billets cannot be considered homogeneous materials. Individual grains dominate the properties of the materials, and the anisotropy of the grains should be taken into account. The random distributions of the grain orientations play an important role in the inhomogeneous deformation in the micro forming processes. These effects should be considered in the model.
2.2 Polycrystalline model
Based on the analysis mentioned above, a new model is developed with the assumption that the grains are hexagon. Considering the effect of free surface, the billets are divided into three portions, namely free surface portion, transition portion and internal portion, as shown in Fig. 1. The free surface portion includes the grains on the free surface of the billets, and the thickness is only one grain or half grain in the radial direction. Due to the slight grain boundary strengthening and less constraint, the flow stress of the grains resembles that of the single crystals in the free surface portion. The flow stress is not homogeneous because of the grain anisotropy, and three grain orientations are considered, namely, á100?, á110? and Schmid factor of 0.5 (sinχ·cosλ≈0.5). The data of flow stress in Refs. [16-17] are used, as shown in Fig.2. The distribution of these three kinds of grain orientations is determined by a stochastic function, and proportion is selected as 5:3:3 randomly. The color of each hexagon in free surface portion shown in Fig. 1 denotes the grain orientation. This model considering grain orientation and its stochastic distribution in the free surface portion is different from the Engel’s model.

Fig. 1 Simulation model
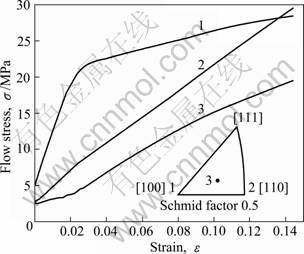
Fig. 2 Flow stress of single crystal
The following portion is the transition portion, which is a layer between the surface portion and internal portion, and its thickness is selected as four grains in the radial direction. Considering the deformation compatibility, the deformation behavior of the grains in this portion is determined by neighboring grains. The flow stress is calculated by
 (1)
(1)
If the strain is assumed to be uniform in the deformation and the strain hardening is considered, Eq. (1) is changed to Eq. (2):
 (2)
(2)
where N is the number of the neighboring grains; σi(εm) is the flow stress of the grains in the transition portion with strain εm; lG is the total grain boundary length; σnG(εm) is the flow stress of the neighboring grains with strain εm; and lc is the contact boundary length of the two neighboring grains.
The last portion is the internal portion, which is considered the polycrystalline material, and the flow stress resembles that of the polycrystalline material. The data in this portion are obtained by the upsetting deformation at room temperature with a column specimen of 3 mm in diameter and 4.5 mm in length.
All the simulations are carried out using the finite element simulation program MSC Superform 2005. The generated model consists of 30 000 quadrilateral four-node elements. The friction factor m is fixed to be 0.1 in all the simulations.
3 Results and discussion
3.1 Experimental preparation of micro upsetting
Compared with the traditional upsetting tests, the micro upsetting tests are different in billet preparation, lubricant and test equipment, etc., because of the miniaturization of the specimen size. There are two basic ways to investigate the size effects in micro forming processes. One way is that the grain size keeps constant when scaling down the dimensions of billets, and another way is that the dimensions of the billets keep constant with increasing the grain size. The latter one is selected in the work.
The commercially pure aluminum was selected as the experimental material, and it was machined to d 1 mm×1.5 mm billet. The heat treatment processes were carried out to get large grain size at 400, 500 and 600 °C for 1 h, and the achieved grain sizes were 37, 57 and 98 ?m, respectively. The tests were carried out with the strain rate of 2×10-3 s-1 at room temperature on the apparatus that was developed by authors. In the apparatus, a high stiffness piezoelectric device was chosen to get high displacement accuracy. A special data collection system was designed for the measurement of the force and displacement during tests [18]. With the presented polycrystalline model, simulations were performed at the strain rate of 2×10-3 s-1.
3.2 Analysis of simulation results
Figure 3 shows the comparison of the flow stress between simulation and experimental results. Three kinds of specimens are used in comparison. The simulation results with grain size L of 98 ?m are more close to the experimental results than those with smaller grain sizes of 37 ?m and 57 ?m. The maximum difference is 10% compared with the experimental results when the gain sizes of 37 ?m and 57 ?m are used. And the flow stress of the simulation results is in the range of experimental results with grain size of 98 ?m.
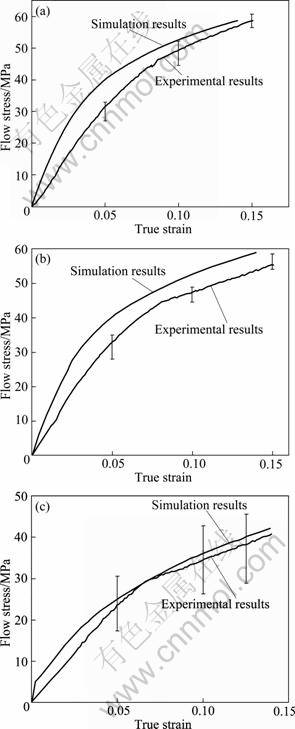
Fig. 3 Comparison of flow stress between simulation and experimental results: (a) L=37 μm; (b) L=57 μm; (c) L=98 μm
In order to investigate the scatter of the flow stress, different distributions of grain orientations in the free surface portion is selected with the same grain orientation and proportion. When the distribution of grain orientation is changed, the flow stress is different, as shown in Fig. 4. This means that the location of single grain has an obvious effect on deformation in micro forming.
Figure 5 shows the distribution of the equivalent stress and strain. It can be clearly seen that inhomogeneous deformation occurs, which is related to the distribution of the grain orientations. The inhomogeneous deformation may lead that the deformed specimen surface is not smooth. To validate the simulation results, contour lines of deformed specimen surface are measured with confocal laser scanning microscope (LEXT 3D OLS3000). A random topography is observed as shown in Fig. 6. This means that the deformation behavior of the billet is affected by each single grain. The result indicates characteristic of micro forming that the deformation is stochastic distribution for the small amount of grains in specimen.
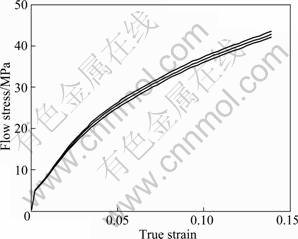
Fig. 4 Effect of grain orientation distribution on flow stress
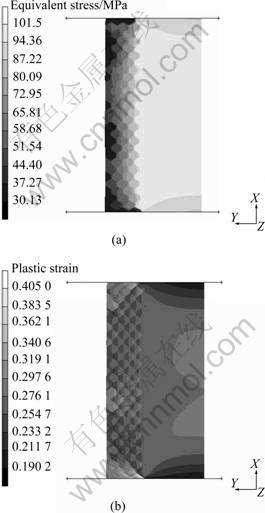
Fig. 5 Distribution of equivalent stress and plastic strain (L=57 ?m): (a) Equivalent stress; (b) Equivalent plastic train

Fig. 6 Contour line of deformed specimen surface (L=57 ?m)
4 Conclusions
1) A new model is presented by dividing the billets into three portions, the surface portion, the transition portion and the internal portion. The grain orientation and its random distribution are considered in the surface portion.
2) The flow stress is different when the distribution of grain orientation is changed, and inhomogeneous deformation is observed. This means that deformation behavior of billets is affected by each single grain.
3) The comparison of the simulation and experimental results shows that the model can be used to simulate the flow stress—strain curves, scattering of the flow stress and inhomogeneous deformation. It confirms that the model is effective for the simulation of micro forming processes.
References
[1] GEIGER M, KLEINER M, ECKSTEIN R. Microforming [J]. Annals of the CIRP, 2001, 50(2): 445-462.
[2] ENGEL U, ECKSTEIN R. Materials mciroforming-from basic research to its realization [J]. Journal of Materials Processing Technology, 2002, 125-126: 35-44.
[3] RAULEA LV, GOVAERT L E, BAAIJENS F P. Grain and specimen size effect in processing metal sheets [C]//GEIGER M. Proceeding of 6th ICTP. Nuremberg, German: Springer Verlag, 1999: 939-944.
[4] KALS T A, ECKSTEIN R. Miniaturization in sheet metal working [J]. Journal of Materials Processing Technology, 2000, 103: 95-101.
[5] RAULEA L V, GOIJAERTS A M, GOVAERT L E, BAAIJENS F P T. Size effects in the processing of thin metal sheet [J]. Journal of Materials Processing Technology, 2001, 115: 44-48.
[6] ENGEL U, EGERER E. Basic research on cold and warm forging of microparts [J]. Key Engineering Materials, 2003, 233-236: 449-456.
[7] ECKSTEIN R, ENGEL U. Behavior of the grain structure in micro sheet metal working [C]//PIETRYZYK M. Proceeding of Metal Forming. Krakow, Poland, 2000: 453-459.
[8] TIESLER N, ENGEL U, GEIGER M. Basic research on cold forging of microparts [C]//KIUCHI M. Proceeding of the 7th ICTP. Yokohama, Japan, 2002: 379-384.
[9] MICHEL J F, PICART P. Size effects on constitutive behaviour for brass in sheet metal forming [J]. Journal of Materials Processing Technology, 2003, 141: 439-446.
[10] ENGEL U, MESSNER A, GEIGER M. Advanced concept for the FE-simulation of metal forming processes for the production of microparts [C]//ALTAN T. Proceeding of 5th ICTP. Colombia, America, 1996: 903-906.
[11] GEISSDOERFER S, ENGEL U, GEIGER M. FE-simulation of microforming processes applying a mesoscopic model [C]//WANG Z R. Proceeding of the 1st ICNFT. Harbin: Harbin Institute of Technology Press, 2004: 141-146.
[12] ENGEL U, GEISSDOERFER S, GEIGER M. Simulation of microforming—An advanced approach applying a mesoscopic model [C]//Proceeding of the 8th ICTP. Verona, Italy: University of Padova, 2005.
[13] KIM D J. KU T W. KANG B S. Finite element analysis of micro-rolling using grain and grain boundary elements [J]. Journal of Materials Processing Technology, 2002, 130-131: 456-461.
[14] YASIN H, ZBIB H M, KHALEEL M A. Size and boundary effects in discrete dislocation dynamics: Coupling with continuum finite element [J]. Materials Science and Engineering A, 2001, 309-310: 294-299.
[15] MARGOLIN H. Polycrystalline yielding-perspectives on its onset [J]. Acta Mater, 1998, 46(17): 6305-6039.
[16] STAUBWASSER W. On work-hardening of aluminium-single crystals (99.99%) and its interpretation [J]. Acta Metallurgica, 1959, 7: 43-50.
[17] HANSEN N, HUAN X. Microstructure and flow stress of polycrystals and single cryastals [J]. Acta Metallurgica, 1998, 46(5): 1827-1836.
[18] WANG Chun-ju, SHAN De-bin, GUO Bin, ZHOU Jian, SUN Li-ning. Key problems in microforming process of microparts [J]. Journal of Materials Science and Technology, 2007, 23(2): 283-288.
微成形工艺数值模拟多晶体模型
王春举, 郭 斌, 单德彬
哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001
摘 要:从坯料的多晶体结构角度考虑自由表面影响构建多晶体模型。该模型中将坯料分为自由表面层、过渡层和内部层三部分。将自由表面层中的晶粒看作单晶体,通过引入晶体取向考虑晶体变形的各向异性,解释塑性变形的非均匀性;在过渡层中,考虑相邻晶粒的影响;在内部层中,将晶粒看作类似多晶体材料变形。使用建立的模型,采用MSC Superform软件模拟镦粗变形过程。模型分析结果表明,坯料塑性变形出现了流动应力的分散性和变形的非均匀性。计算结果与试验结果吻合较好,这说明建立的模型是有效的。
关键词:微成形;尺寸效应;多晶体模型;非均匀变形
(Edited by LI Xiang-qun)
Foundation item: Projects (50835002, 50805035) support by the National Natural Science Foundation of China; Project (QC08C55) supported by the Natural Science Foundation of Heilongjiang Province, China; Project (200802131031) supported by the PhD Programs Foundation of Ministry of Education of China for Young Scholars
Corresponding author: WANG Chun-ju; Tel: +86-451-86418640; E-mail: cjwang1978@hit.edu.cn
DOI: 10.1016/S1003-6326(11)60866-2