DOI： 10.11817/j.issn.1672-7207.2020.05.012

差异变形下地铁盾构隧道内行车舒适性研究

施成华¹,刘建文¹,李翔¹,雷明锋^{1, 2},彭立敏¹

（1. 中南大学 土木工程学院，湖南 长沙，410075；

2. 重载铁路工程结构教育部重点实验室，湖南 长沙，410075）

摘要:针对地基沉降、临近施工扰动导致的工后差异变形广泛存在于我国已建地铁盾构区间隧道中，对隧道内的行车安全性和舒适性会产生影响等问题，基于赫兹非线弹性接触理论，考虑车辆、轨道、隧道、围岩的空间结构特征和相互接触关系，建立车-轨-隧-围岩一体化计算模型，计算隆起变形下盾构隧道内运行车辆的轮重减载率及平稳性指标，分析地铁列车行车安全性及舒适性。从线路轨向高差和行车速度这2个主要因素出发，讨论其对行车舒适性的影响规律，探讨不同线路隆起情况下平稳行车的临界速度。研究结果表明：当盾构隧道隆起值在容许范围内且列车以正常运行速度行驶时，能够保证列车的行车安全，但对列车运行舒适性影响较大；行车舒适性与行车速度和隧道隆起程度有关，行车速度的影响程度较明显；当隧道轨向高差达到规范规定的预警值时，平稳行车速度约为80 km/h；当达到控制值时，满足行车舒适性要求的车速仅为20 km/h左右。

关键词:地铁盾构隧道；车-轨-隧-围岩一体化模型；差异变形；行车舒适性

中图分类号:U456.2      文献标志码:A           开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）05-1279-10

Study on traffic comfort in metro shield tunnel during differential deformation

SHI　Chenghua¹, LIU　Jianwen¹, LI　Xiang¹, LEI　Mingfeng^{1, 2}, PENG　Limin¹

(1. School of Civil Engineering, Central South University, Changsha 410075, China；

2. MOE Key Lab of Heavy Haul Railway Engineering Structure, Central South University,Changsha 410075, China)

Abstract: Considering that differential deformation after construction caused by ground settlement and nearby construction disturbance exists widely in metro shield tunnel, which may lead to significant influence on the security and comfort of the operational metro system,based on Hertz non-linear elastic contact theory,the spatial structural characteristics and contact relations of vehicles, tracks, tunnels and surrounding rocks were considered,an integrated calculation model of vehicle-rail-tunnel was established. The wheel load reduction ratio and comfort index of running vehicles with uplift deformation were calculated.The security and comfort of metro trains in shield tunnels during uplift deformation were analyzed.Accounting for the two main factors including the peak value of the rail height difference and the running speed of the train,the mechanism of the two factors on the operational security and comfort was discussed, and the critical speed of steady driving under different line heave conditions was discussed. The results show that when the tunnel heave is within the allowable range and the train running with normal velocity, the operation safety of train can be ensured, while the operation comfort will be greatly affected. The operation comfort of train is related to its running speed and the tunnel heave, and the velocity of train has greater impact on the operation comfort .When the peak value of the rail height difference reaches the warning value specified in the standard, the velocity for steady driving is about 80 km/h. When the allowable limit is reached, the vehicle speed meeting the operation comfort requirements is only about 20 km/h.

Key words: metro shield tunnel; train-track-tunnel-soil interaction model; differential deformation; operational comfort

随着城市化的不断发展，在既有地铁隧道邻近区域进行基坑开挖的现象频繁，国内外学者对此类问题进行了深入研究^[1-3]。郑刚等^[4]总结了近年来国内基坑施工引起盾构隧道变形的代表性工程案例，其中邻近基坑开挖引起盾构隧道最大隆起量可达33 mm。基坑开挖引起的土体卸载会破坏下方既有地铁隧道的应力平衡，造成隧道线路局部隆起，不仅引起隧道结构管片开裂、螺栓屈服、接缝张开及渗漏水等病害，而且影响隧道内行车安全性及舒适性，因此，对隆起变形下隧道内列车运行动力性能进行研究尤为重要。国内外学者对列车行车安全性与平稳性开展了大量研究。CHENG等^[5]基于线性蠕变模型，推导出曲线上铁道车辆运动的振动微分方程，采用线性和非线性模型分析了不同曲线半径的轨道条件下车速对安全性和平稳性的影响；张小会等^[6]研究了行车速度及路基不均匀沉降对列车动力性能的影响。YAU^[7]研究了在不均匀沉降的导轨梁上运行的磁悬列车动力响应问题，发现即使不均匀沉降很小，在车速较大的情况下，列车动力响应也会有明显放大的现象。RECUERO等^[8]提出了一种能够有效地捕捉到中频车辆-轨道相互作用、接触片弹性和车辆动力学规律的方法。JU等^[9]研究了一系列磁浮列车在多跨桥梁基础沉降和地震作用下的安全性问题。杨吉忠等^[10-11]运用车辆-轨道耦合动力学模型对有砟轨道下沉变形特性、横风中的列车运行安全性进行了研究。CHELI等^[12]分析了轨道不平顺对车体振动的影响，发现不同振动模态的激励对行车舒适性有很大影响。事实上，列车在地面路基上与地下隧道中行驶时，由于行车所处的环境不同，车辆振动与平稳性也有差别。当前，大量研究关注于地铁行车引起的隧道结构动力响应及周围环境的振动，具有代表性的有NEJATI等^[13]的2D模型、GALVIN等^[14]的2.5D模型、FORREST等^[15]的“Pipe-in-Pipe”模型、YANG等^[16-17]的盾构隧道振动激励模型试验等，而关于地铁内行车安全性与平稳性的研究很少。当前大部分研究一般以铁路轨道不平顺谱作为外部激励，忽略了车辆、轨道、盾构隧道与围岩之间的相互作用，通常将邻近基坑开挖对既有盾构隧道的影响和列车行车安全性、舒适性分开单独进行研究，无法揭示地铁线路差异变形对列车行车产生的影响。为此，本文作者以1个基坑开挖引起既有下卧地铁线路隆起变形的工程案例为研究背景，建立车-轨-隧-围岩一体化模型，开展差异变形下地铁盾构隧道内行车舒适性研究，进而对行车舒适性影响因素进行分析并对列车行车舒适性限值进行讨论。

1 工程简介

1.1　工程概况

深圳市桂庙路快速化改造工程西起规划振海路，终于南海大道，道路全长约4.9 km。桂庙路改造工程需在既有地铁11号线上采用明挖法修建双洞矩形公路隧道，共线长度约3 km。其中，K3+840～K3+980段内基坑与地铁相对位置关系如图1所示。

图1　基坑与下卧盾构隧道相对位置关系

Fig. 1　Relative position between excavation and underlying shield tunnel

基坑开挖深度约20 m，宽度约40 m，围护结构为地下连续墙，墙厚1 m，深度约30 m。共线段地铁11号线盾构隧道左、右两线均位于基坑下方，隧道内径为6 m，壁厚0.35 m，与基坑底板净距约 8 m。该标段内地层自上而下依次为素填土(厚2~3 m)、砾质黏性土(厚7~10 m)和粗砾花岗岩(厚20~25 m)。为保证施工进度和土体稳定性，设计采用全幅、分层、分步开挖，施工步长为6 m。

1.2　现场监测

基坑开挖时，除加强基坑监测外，开挖引起的隧道隆起变形会对运营列车的行车安全性和舒适性产生不利影响，因此，对下卧地铁11号线变形的监测尤为重要。将工程施工区域往两端各延伸20 m作为开挖影响区域，在影响区域内，间隔2.5 m布置监测断面，每个监测断面共布置4个监测点，分别位于道床，左、右拱腰和拱顶。

在工程建设过程中，K3+840～K3+980段地铁11号线发生明显隆起变形，实测左线隆起峰值已超过施工阶段控制值10 mm，截至目前自动化监测隆起峰值基本稳定在14 mm左右。

2 车-轨-隧-围岩一体化模型

随着计算机性能的提高和计算方法的发展，对于涉及基坑开挖引起下卧盾构隧道隆起变形的静力计算过程和隆起变形后地铁列车运营安全性、舒适性的动力计算，大多采用有限元法。为此，本文基于ABAQUS有限元平台，根据赫兹非线弹性接触理论模拟轮轨接触关系，考虑车辆、轨道、隧道、围岩的空间结构特征和相互接触关系，建立车-轨-隧-围岩一体化模型，具体包括地铁车辆模型、轮轨接触模型、轨道模型及隧道-围岩模型，以研究基坑开挖引起的隧道差异变形对地铁行车的影响。

2.1　地铁车辆模型

根据地铁车辆结构特点，车辆动力学模型包含车体、转向架以及轮对3种结构。车体与转向架之间通过二系悬挂弹簧连接，转向架与轮对之间通过一系悬挂弹簧连接。根据Hamilton原理建立车辆结构的动力学方程，该模型中车体、转向架和轮对采用实体单元模拟，用弹簧阻尼单元模拟一系、二系悬挂系统连接，地铁车辆模型如图2所示^[18]。

图2　地铁车辆模型

Fig. 2　Metro vehicle model

2.2　轮轨接触模型

列车运行时，轮轨之间的相互关系可概化为图3所示的移动非线性Hertz弹簧模型。轮轨接触的法向力可采用如下公式计算^[19]：

(1)

式中：P(t)为轮轨接触法向力；ΔZ(t)为接触点处轮轨间的法向弹性压缩量；G为轮轨接触常数。

图3　轮轨接触模型

Fig. 3　Wheel-rail interaction model

2.3　轨道模型

本案例地铁道床形式为短轨枕式整体道床，轨道振动主要体现在钢轨的振动上，钢轨与道床之间采用弹簧阻尼元件连接。仅考虑其垂向、横向及扭转自由度，图4所示为短枕式整体道床轨道动力模型纵断面图和横断面图。

图4　轨道动力学模型

Fig. 4　Dynamic models of track

2.4　隧道-围岩模型

管片是盾构隧道最基本的单元，接头的存在是其最显著的特征。为准确模拟管片与管片、管片与围岩之间相互接触关系，基于三维非线性接触理论建立多尺度精细化三维盾构隧道-围岩模型，管环分为1个封顶块K(圆心角为21.5°)、2个邻接块B(圆心角为68°)和3个标准块A(圆心角为67.5°)，管环宽度为1.5 m，衬砌环接缝采用12个纵缝螺栓(M27)和16个环缝螺栓(M27)连接，错缝拼装。螺栓采用弯梁单元模拟，并将梁单元嵌入管片单元中，既可模拟接头的拉、压、剪切力学性质，也可模拟管片之间的相互作用。为提高计算效率，在基坑开挖影响范围外，隧道采用等效均质模型，刚度折减系数经验值取为0.78。管片与管片、管片与围岩之间的接触面法向行为均采用“硬接触”关系模拟。在接触面切向行为中，若接触面闭合，则接触面定义为可传递摩擦力。SHI等^[1,20]介绍了该模型，并成功地应用于邻近基坑开挖对盾构隧道的影响研究和列车动载作用下管片结构静动力响应特性研究。

通过对本文工程案例进行分析，数值模型中隧道及线路的隆起变形主要通过隧道上部基坑开挖卸荷实现。模型主要针对K3+846 ~ K3+946段，共计100 m，基坑长30 m，宽40 m，深20 m，与地铁隧道净距为8 m。基坑开挖模型如图5所示。开挖分为6层10步进行(图5中间位置数据1~10表示开挖步序)，在基坑施工过程中，考虑围护结构及支撑的作用。建立的车-轨道-隧道-土体三维动力学耦合模型局部放大图如图6所示。

图5　基坑开挖模型

Fig. 5　Excavation model

图6　车-轨-隧耦合动力学模型

Fig. 6　Dynamic train-track-tunnel-soil coupled model

3 模型参数与模型验证

3.1　模型参数

采用瑞利阻尼模型(Rayleigh damping)，由质量阻尼系数α和刚度阻尼系数β确定模型中阻尼比系数。围岩与衬砌结构的相关力学参数见表1。地铁车辆为B型车，车辆及轨道模型参数见表2。

3.2　模型验证

为验证本文静、动力模型的有效性，基坑开挖引起下卧盾构隧道隆起变形(静力过程)采用案例验证，计算结果与现场实测结果对比见图7。列车荷载作用下隧道结构动力响应(动力过程)的验证可基于文献[21]中上海地铁9号线隧道振动实测值采用本文模型进行，隧道壁加速度频谱的计算值与实测值对比见图8。

由图7可知：基坑开挖所致隧道隆起变形的模型计算结果与现场实测结果基本吻合，且模拟计算的各测点隆起值随开挖步的变化也与实测结果一致。同时，图8表明采用本文中的车-轨-隧-围岩一体化模型计算得到的加速度谱与现场实测结果较吻合，验证了本文所采用的计算模型计算静、动力的有效性与准确性。

图7　隧道隆起变形曲线对比

Fig. 7　Comparison between simulations and measurements of tunnel heave

图8　隧道壁加速度频谱对比

Fig. 8　Comparison between simulation values and measurement values of acceleration spectrum on tunnel side wall

表1　围岩与衬砌相关力学参数

Table 1　Related mechanical parameters of soil and lining

表2　车辆与轨道相关力学参数

Table 2　Related mechanical parameters of vehicle and track

4 列车动力性能分析

4.1　行车安全性分析

在车-轨耦合系统分析中，常选取脱轨系数和轮重减载率作为评估列车运行安全性的主要指标。轮重减载率一般用于轮对横向力等于零的情况，适用于本文研究对象。

分别提取隧道隆起变形为15 mm、行车速度为72 km/h时首节车厢第1和第2轮对处车轮与轨道之间的竖向接触力，计算并绘制轮重减载率时程曲线，如图9所示。

图9　轮重减载率时程曲线

Fig. 9　Time-history of wheel load reduction ratio

由图9可知：各轮对轮重减载率时程曲线均呈现“增—减—增—减”趋势，每条时程曲线中第1个波峰出现在列车刚驶入隆起段线路，车轨接触不稳定，减载率较大；第1个波谷出现在列车稳定行驶在隆起线路段，该时段列车行驶平稳，轮重减载率较低；第2个波峰也是该时程曲线的峰值，出现在轮对刚刚驶过线路的隆起顶点即t=0.63 s和0.74 s时，此时，列车车轮由“上坡”变为“下坡”，出现类似于“跳车”的现象是最危险的时段。

以上2轮对轮重减载率最大值分别为0.020 9和0.023 96，与规范^[22]规定的标准值0.600 00相差甚远。可见：当列车以正常运行速度行驶在隆起程度不超过规范控制值且无明显横向荷载的盾构隧道段时，地铁列车不易出现脱轨事故，行车安全性较高。

5.2　行车舒适性分析

国内常用列车车体振动加速度及平稳性指标2个标准来评判列车行车舒适性^[22]，本文选取后者进行分析研究。我国列车运行平稳性指标W采用Sperling指标：

(2)

式中：A为列车车体振动加速度；f为列车振动频率；F( f )为频率修正系数。规范^[22]规定：当地铁列车运行平稳性指标W≤2.50时，行车舒适性评级为“优”；当2.50

由图10可知：列车行驶在线路隆起段时，垂向加速度时程曲线除自身震荡外，总体上呈现一定的波动性，前车厢垂向加速度峰值为0.058 m/s²，后车厢垂向加速度峰值为0.053 m/s²。车厢垂向振动加速度时程曲线变化趋势为：列车行驶在隆起前半段即“爬坡”段，对应时间分别为前车厢0.5~1.0 s，后车厢1.5~2.0 s，垂向加速度均值出现正向峰值；达到隆起段顶点时(前车t=1.0 s，后车t=2.0 s)，垂向加速度均值降到0 m/s²左右；在行车“下坡”段(前车1~2 s、后车2~3 s)，车辆垂向加速度均值呈现负值，之后稳定在0 m/s²左右震荡。

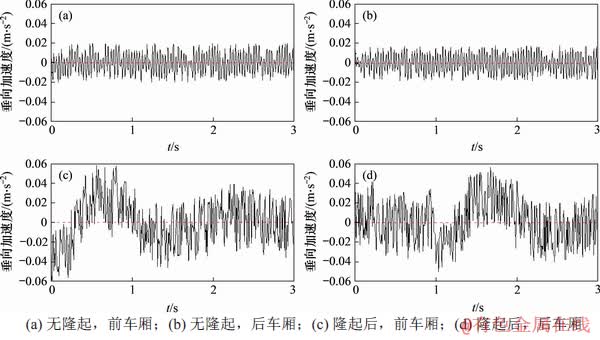
图10　车厢垂向振动加速度-时程曲线

Fig. 10　Vertical acceleration-time curves of vehicle

计算前后车行车平稳性指标分别为2.577 1与2.549 5，可见地铁列车运行在该线路隆起段时，前后两车厢平稳性指标均不达标，仅处于“良”等级，不满足规范中“优”的要求，且前车行车舒适性比后车略差。

5 行车舒适性影响因素分析

经过以上分析可知：不考虑其他荷载因素，当地铁列车行驶在基坑开挖引起的隧道线路隆起段时，列车在正常运行速率下行驶不会出现安全问题，但地铁列车大多为客车，所以，需要满足乘客乘坐的舒适性即列车运行舒适性要求。这里对隆起变形下盾构隧道内行车舒适性影响因素进行研究，着重考虑隧道隆起程度和列车行车速度2个主要因素。

5.1　隧道隆起程度

隧道隆起程度主要通过轨向高差体现。选取隧道隆起变形峰值为5，10，15和20 mm时对应的轨向高差1.4，2.1，3.4和4.3 mm/(10 m)作为隧道隆起变形量，提取隧道不同隆起变形工况下前车垂向加速度时程曲线，如图11所示。

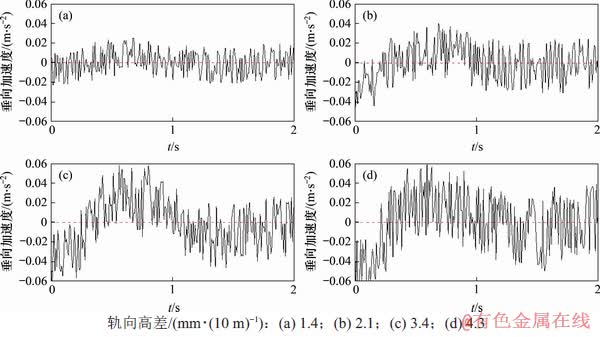
图11　不同隆起工况下车体垂向加速度-时程曲线

Fig. 11　Vertical acceleration-time curves of vehicle in different tunnel heave cases

由图11可知：在各工况下，车体垂向振动加速度峰值分别为0.023，0.045，0.058和0.065 m/s²，可见线路钢轨轨向高差在一定程度上影响列车运行振动加速度；隆起值越大，车体垂向加速度越大。对以上4条曲线进行快速傅里叶变换，求解其平稳性指标，如图12所示。

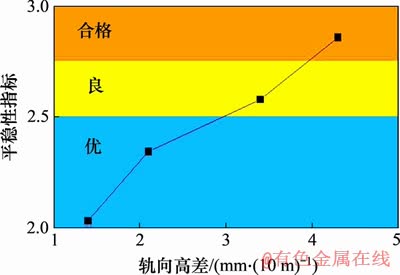
图12　盾构隧道隆起值与平稳性指标关系

Fig. 12　Relationship between tunnel heave and stability index

从图12可见：列车平稳性指标与线路轨向高差值基本上呈线性关系；当轨向高差达到3.4 mm/(10 m)时，行车平稳性指标已经超过规范规定值2.500 0；当轨向高差达4.3 mm/(10 m)时，行车平稳性指标达到2.856 7，按照规范评级为“合格”，不满足规范规定的“优”的标准，极有可能出现乘客乘坐不舒适问题。

5.2　行车速度

分别提取36，54，72，90和108 km/h共5种车辆运行速率下后车车体的垂向振动时域曲线，并进行平稳性指标求解，结果如图13所示。

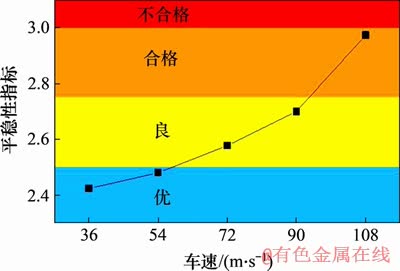
图13　列车运行速率与平稳性指标的关系

Fig. 13　Relationship between train running speed and stability index

由图13可知：平稳性指标相对于行车速率增大呈现指数增大趋势；当行车速率低于54 km/h时，列车运行平稳性指标处于规范值2.500 0以内，乘客乘行车舒适性较好；当车速达到72~90 km/h时，平稳性指标处于2.500 0~2.750 0之间，行车舒适性评级为“良”；当车速增大到108 km/h后，平稳性指标迅速增大，达到2.973 4，处于合格线边缘，此时列车运行舒适性较差，无法满足乘客乘坐的舒适性要求。

5.3　列车行车舒适性限值讨论

由以上分析可知，当地铁列车行驶在隧道隆起段时，行车平稳性指标与隧道隆起程度及列车行车速度均呈正相关关系，针对上述2个因素共20个工况下的平稳性指标数据进行二元回归分析，得到列车运行平稳性指标W与隧道隆起程度、行车速度的关系：

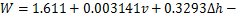
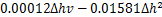(3)

式中：v为列车运行速率，km/h；Δh为盾构隧道轨向高差最大值，mm/(10 m)。由式(3)计算得到平稳性指标为2.50，2.75和3.00时的Δh-v曲线，见图14。

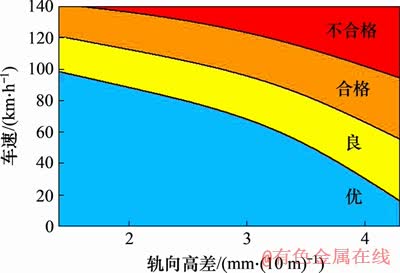
图14　平稳行车车速与线路轨向高差的关系

Fig. 14　Relationship between train velocity and rail altitude difference

由图14可知：当隧道轨向高差峰值达到规范规定预警值2 mm/(10 m)时，平稳行车速度约为80 km/h；当隧道轨向高差峰值达到规范控制值4 mm/(10 m)时，平稳行车速度仅为20 km/h左右，若超过此速度行驶，则会产生舒适性问题，乘客行车舒适性降低；当地铁列车平稳行车时，其车速与隧道轨向高差峰值呈现负相关关系，隧道轨向高差峰值越大，平稳行车车速越低；当盾构隧道轨向高差峰值超过3.5 mm/(10 m)时，列车平稳运行车速下降明显，此时，为了达到平稳行车要求，需对车速进行控制。

6 结论

1) 基于赫兹非线弹性接触理论，考虑车辆、轨道、隧道、围岩的空间结构特征和相互作用关系，构建了车-轨-隧一体化计算模型，建立了差异变形影响下盾构区间隧道内行车舒适性的计算方法。

2) 采用建立的计算模型，分析了隆起变形下盾构隧道内运行车辆的安全性和舒适性。当盾构隧道隆起变形不超过规范控制值且地铁列车以正常运行速度行驶时，能够保证隧道内的行车安全，但会对隧道内列车运行的舒适性产生一定影响。

3) 地铁列车以正常运行速度行驶在线路隆起段时，由车体垂向振动加速度计算得出的平稳性指标与线路轨向高差呈现线性关系，与行车速度呈指数关系；当隧道轨向高差达到规范规定预警值2 mm/(10 m)时，平稳行车速度约为80 km/h；当达到控制值4 mm/(10 m)时，满足行车舒适性要求的车速仅为20 km/h左右。

参考文献：

[1] SHI Chenghua, CAO Chengyong, LEI Mingfeng, et al.Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints[J]. Tunnelling and Underground Space Technology, 2016, 51(1): 175-188.

[2] LIANG Rongzhu, XIA Tangdai, HUANG Maosong, et al.Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect[J]. Computers and Geotechnics, 2017, 81(1): 167-187.

[3] HUANG Xu, SCHWEIGER H F, HUANG Hongwei. Influence of deep excavations on nearby existing tunnels[J]. International Journal of Geomechanics, 2013, 13(2): 170-180.

[4] 郑刚, 杜一鸣, 刁钰, 等. 基坑开挖引起邻近既有隧道变形的影响区研究[J]. 岩土工程学报, 2016, 38(4): 599-612.

ZHENG Gang, DU Yiming, DIAO Yu, et al. Influenced zones for deformation of existing tunnels adjacent to excavations [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 599-612.

[5] CHENG Y C, HSU C T. Running safety and comfort analysis of railway vehicles moving on curved tracks[J]. International Journal of Structural Stability and Dynamics, 2014, 14(4): 1450004.

[6] 张小会, 周顺华, 宫全美, 等. 路基不均匀沉降对车辆和轨道动力响应的影响[J]. 同济大学学报(自然科学版), 2015, 43(8): 1187-1193, 1253.

ZHANG Xiaohui, ZHOU Shunhua, GONG Quanmei, et al. Effect of subgrade differential settlement on dynamic response of vehicle and slab track vertical coupled system[J]. Journal of Tongji University(Natural Science), 2015, 43(8): 1187-1193, 1253.

[7] YAU J D. Response of a maglev vehicle moving on a series of guideways with differential settlement[J]. Journal of Sound and Vibration, 2009, 324(3/4/5): 816-831.

[8] RECUERO A M, ESCALONA J L. Dynamics of the coupled railway vehicle–flexible track system with irregularities using a multibody approach with moving modes[J]. Vehicle System Dynamics, 2014, 52(1): 45-67.

[9] JU S H, LEONG C C, HO Y S. Safety of maglev trains moving on bridges subject to foundation settlements and earthquakes[J]. Journal of Bridge Engineering. School of Transporation Engineering 2014, 19(1): 91-100.

[10] 杨吉忠. 考虑空气动力效应时高速列车运行安全平稳性研究[D]. 成都: 西南交通大学交通运输工程学院, 2010: 60-70.

YANG Jizhong. Aerodynamic effect on running safety and stability of high-speed train[D]. Chengdu:Southwest Jiaotong University. School of Transportation Engineering, 2010: 60-70.

[11] 高建敏, 翟婉明, 徐涌. 铁路有砟轨道下沉及高低不平顺发展预测研究[J]. 中国铁道科学, 2009, 30(6): 132-134.

GAO Jianmin, ZHAI Wanming, XU Yong. Study on the settlement of railway ballasted track and the growth forecast of track vertical profile irregularity[J]. China Railway Science, 2009, 30(6): 132-134.

[12] CHELI F, CORRADI R. On rail vehicle vibrations induced by track unevenness: Analysis of the excitation mechanism[J]. Journal of Sound and Vibration, 2011, 330(15): 3744-3765.

[13] NEJATI H R, AHMADI M, HASHEMOLHOSSEINI H. Numerical analysis of ground surface vibration induced by underground train movement[J]. Tunnelling and Underground Space Technology, 2012, 29: 1-9.

[14] GALVIN P, FRANCOIS S, SCHEVENELS M, et al. A 2.5D coupled FE-BE model for the prediction of railway induced vibrations[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(12): 1500-1512.

[15] FORREST J A, HUNT H E M. Ground vibration generated by trains in underground tunnels[J]. Journal of Sound and Vibration, 2006, 294(4/5): 706-736.

[16] YANG Wenbo, CUI Ge, XU Zhaoyang, et al. An experimental study of ground-borne vibration from shield tunnels[J]. Tunnelling and Underground Space Technology, 2018, 71(1): 244-252.

[17] YANG Wenbo, LI Lingui, SHANG Yingchao, et al. An experimental study of the dynamic response of shield tunnels under long-term train loads[J]. Tunnelling and Underground Space Technology, 2018, 79(9): 67-75.

[18] XU Qingyuan, OU Xi, AU F T K, et al. Effects of track irregularities on environmental vibration caused by underground railway[J]. European Journal of Mechanics: A, 2016, 59(9): 280-293.

[19] 翟婉明. 车辆—轨道耦合动力学[M]. 北京: 科学出版社, 2015: 40-41.

ZHAI Wanming. Vehicle-track coupled dynamics[M]. Beijing: Science Press, 2015: 40-41.

[20] 艾辉军, 彭立敏, 施成华. 基于三维非连续接触模型的管片接头静动力特性分析[J]. 岩土工程学报, 2013, 35(11): 2023-2029.

AI Huijun, PENG Limin, SHI Chenghua. Static and dynamic characteristic analysis of segment joints based on three-dimensional discontinuous contact model[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2023-2029.

[21] 黄强, 姚湘静, 黄宏伟, 等. 地铁运行时轨道-隧道-地层振动实测与分析[J]. 振动·测试与诊断, 2018, 38(2): 260-265, 416.

HUANG Qiang, YAO Xiangjing, HUANG Hongwei, et al. Field measurement and analysis of train-induced vibration in the whole track-tunnel-ground system[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(2): 260-265, 416.

[22] GB/T 7928—2003. 地铁车辆通用技术条件[S].

GB/T 7928—2003. General technical specification for metro vehicles[S].

（编辑 陈灿华）

收稿日期： 2019 -08 -20; 修回日期： 2019 -11 -20

基金项目(Foundation item)：国家重点研发计划项目(2017YFB1201204)；国家自然科学基金资助项目(51778636)；中南大学中央高校基本科研业务费专项资金资助项目(2019zzts072) (Project(2017YFB1201204) supported by the National Key R&D Program of China; Project(51778636) supported by the National Natural Science Foundation of China; Project(2019zzts072) supported by the Fundamental Research Funds for the Central Universities of Central South University)

通信作者：刘建文，博士研究生，从事隧道与地下工程研究；E-mail: jwenliu@csu.edu.cn