竹材组合墙体的热湿耦合传递数值模型

苏林，李念平，黄从健，王廷伟

(湖南大学 土木工程学院，湖南 长沙，410082)

摘要：根据Luikov多孔介质热湿耦合传递理论，分析竹材组合墙体在考虑相变、热湿扩散等因素下的热湿耦合传递特性。对热湿耦合传递基本方程进行合理简化，并确定其边界条件和初始条件，建立求解竹材组合墙体热湿耦合传递特性的数值计算模型。在室外气候作用下，对处于非稳态工况下墙体的热湿耦合传递特性进行一维数值模拟，并将模拟结果与其在相应工况下的实验结果进行对比，发现室内温度、相对湿度等参数的模拟值与实验值具有较好的一致性，说明所建立的热湿耦合传递数值模型能较好地描述竹材组合墙体的耦合非稳态传递特性。

关键词：建筑节能；多孔介质；热湿耦合传递；数值模型

中图分类号：TU111            文献标志码：A         文章编号：1672-7207(2012)S1-0204-05

Numerical model of coupled heat and moisture transfer in bamboo composite wall

SU Lin, LI Nian-ping, HUANG Cong-jian, WANG Ting-wei

(College of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract: Heat and moisture transfer characteristics, which consider the phase transition, heat and moisture diffusion in the bamboo composite wall, were investigated based on the Luikov coupled heat and moisture transfer model in porous media. The basic heat and moisture transfer equations were simplified, the initial and boundary conditions were defined, and a new numerical model for calculating the transfer characteristics of the wall was developed. Under the natural climatic conditions, the one-dimensional and unsteady-state coupled heat and moisture transfer characteristics of the wall were simulated, the results were compared with the experimental data for temperature and moisture content and good agreement was observed. Thus it can be seen that the numerical model is reliable for describing the unsteady-state coupled heat and moisture transfer characteristics.

Key words: building energy conservation; porous media; heat and moisture transfer; numerical model

我国的竹类资源十分丰富，竹材性能良好，具有很多优点，比如生长快，产量高，强度大，可再生，而且对环境保护十分有利等特点，因此用竹材作为建筑材料建造房屋是一种很有潜力的选择，也是一个新的发展方向，以竹代木正成为一个新的发展趋势^[1]。

然而一直以来，由于工艺和工具的落后，竹材长期停留在以原竹的形式或经过简单、粗糙的加工处理用于建筑业，技术含量较低，并且无法充分发挥竹材的性能优势。随着我国科学技术的发展，竹材的开发和利用在一定程度上得到了发展，竹材在建筑行业的利用也从简单的单一竹材利用方式向复合化和高性能等方向发展，如竹材胶合板、竹篾帘复合板、竹帘人造板等一批有代表性的产品应运而生^[2]。以竹胶合板为基本特征的竹质结构板材产品和种类日益增多，在建筑、车辆、造船等众多领域都获得了广泛的应用，充分显示了竹材人造板所具有的优良特性^[3]。

通过改善建筑物围护结构的热工性能，在夏季可减少室外热量传入室内，在冬季可减少室内热量的流失，使建筑热环境得以改善，从而减少建筑冷热量消耗。冬季墙体内表面上如果冷凝结露形成水滴很容易被发现，但墙体内部析出的水分却不易被察觉，但其后果至少就墙体本身来说却更为严重。墙体内的湿积累会引起建筑材料保温性能下降，强度降低，长霉，并有可能产生对人体有害的细菌^[4]。而季节性的冻融过程将直接制约着湿、热迁移的规律，给工程建设造成影响，特别是冻胀现象会出现破坏性的挤压应力。

1  多孔介质的热湿传递机理

1.1  多孔介质热湿传递的研究现状

多孔介质内热湿迁移是由“推动势”推动的。因此，根据选择的推动势不同，建立的数学模型也不同。有关多孔介质的理论研究近50年，国内外学者根据不同迁 移势提出了不同的数学模型。早在1856年，Darcy对法国Dijon城的地下水源进行了研究，提出了著名的适用于一定条件下多孔介质中流体流动的Darcy定律。1934年Luikov提出了热湿耦合传递模型；1939年Henry根据蒸发冷凝理论提出相应的数学模型；1957年Philip和DeVries以温度梯度和含湿量梯度为驱动势建立了热湿耦合模型；Berger和Per于1973年以及Whitaker于1977年根据不同的驱动势分别建立了相应的数学模型。这些数学模型存在的主要问题是没有计算热湿的物性参数，并且由于模型的高度非线性耦合，给求解带来了困难。目前，求解这类耦合方程的数学方法包括Laplace变化、积分变化。这些都有特定的边界条件。多孔介质内部热湿传递机理见表1^[5]。

1.2  Luikov模型假设和简化

Luikov建立了一组耦合偏微分方程用来描述毛细管多孔介质的热湿传递。Luikov假设湿传递与热传递类似，并且毛细管传递过程的强弱与温、湿度梯度大小成比例^[6-7]。Luikov模型被认为是较为可靠并且实用的，因为温度梯度也是影响介质中湿传递的一个重要因素。由于多孔介质中的液态水流动导致了湿传递和热传递的相互关联，当液态水在介质内蒸发时这种关联性更加密切。因此，将热传递方程跟湿传递方程分开并不能真实地描述湿材料内部的热湿传递现象。鉴于此，Luikov在不可逆热力学理论的基础上提出了热湿耦合传递理论。

本文作者就对Luikov模型进行分析简化，并利用

表1  多孔介质的内部热湿传递机理

Table 1  Heat and moisture transfer mechanism in porous media

它进行数值模拟，分析Luikov模型与实际实验数据的吻合情况。

为了对Luikov模型进行简化，我们做出如下假设：

(1) 竹材的热物性参数恒定不变。

(2) 竹材的初始温、湿度在竹材各处是相等的。

(3) 不考虑重力作用，因为毛细管压力作用远强于重力的作用。

(4) 竹材内部固相物质的形变不予考虑。

(5) 竹材内部无内热源。

基于以上假设，可以得出竹材的三维热湿耦合传递方程如下^[8-14]：

(1) 热传递方程

   (1)

(2) 湿传递方程

      (2)

式中：r为竹材密度；c_q为比热容；T为热力学温度；t为时间；k_q为导热系数；k_m为导湿系数；e为水蒸气扩散系数；l为潜热；d为热梯度系数；c_m为比湿容量；U为湿度势。

边界条件为：

   (3)

      (4)

初始条件：

T=T₀                   (5)

U=U₀                   (6)

U与含湿量C有如下关系：

C=c_mU                 (7)

2  实验与数值模拟

2.1  实验条件

该实验房建在湖南大学暖通实验楼的楼顶，尺寸(长×宽×高)为2 m×2 m×2 m，方位为正南北方向，在实验房的北面有一扇0.6 m×0.8 m的小木门，四周为空旷地区(如图1所示)。其墙体构成材料及结构示意图如图2所示，墙体各层材料的热物性参数详见  表2。

图1  实验房的外观照片

Fig.1  Photo of experimental house

2.2  实验结果与分析

本次实验数据选取长沙地区7月份某天连续24 h的温度、湿度情况，每间隔1 h记录1次数据。温度传感器采用PT100铂电阻，湿度传感器采用Honeywell 4030等。在实验房间的屋顶及每面墙上按要求均匀布置同种传感器至少3个，取3个传感器读数的平均值为最终数据，以减小误差的影响。该实验时段实测实验房内外空气温度如图3所示。

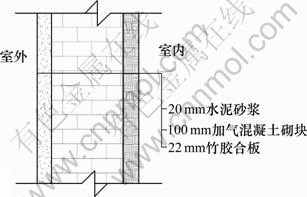
图2  实验房的墙体结构示意图

Fig.2  Structure diagram of wall of experimental house

从图3可以发现室内平均温度比室外平均温度至少低2.5 ℃，另外，从图3中还可以发现室内空气温度变化的波形要比室外空气温度变化的波形延迟了一段时间，如室内空气温度达到峰值的时间在17:00左右，而室外空气温度达到峰值的时间在15:00左右。分析其原因应当是新型竹材组合墙体热惰性指标较大，即蓄热能力较强，使得室内空气温度的变化较室外的既衰减又延迟，因此，该新型竹材组合墙体的保温隔热性能良好。

2.3  模拟与实验结果的对比分析

利用商用流体与传热计算软件Fluent对竹材组合墙体的热、湿耦合传递进行数值模拟^[15]，将材料的热物性参数及初始边界条件输入Fluent，待迭代收敛后导出相关数据，并进行分析。

图4所示为室内空气温度的模拟值与实测值的对比，图5所示为室内空气相对湿度模拟值与实测值的对比。图4和5中室内空气温度和相对湿度的变化是建立在外界为自然环境即非稳态情况下的，已知室外的环境温度、湿度、太阳辐射等变化情况，已知墙体的导热系数、热扩散系数、对流换热系数、湿扩散系数、对流传质系数等等，计算求得室内的温度、湿度变化情况。从图4和5中可以看到温度和相对湿度的模拟值与实测值吻合较好，说明提出的热湿耦合传递数值模拟的准确度较高，可以较好地模拟环境温度、湿度变化工况。

表2  墙体各层材料的热物性参数

Table 2  Thermo-physical parameters of materials for wall

图3  实验房内外空气的温度

Fig.3  Measured values of indoor and outdoor air temperature

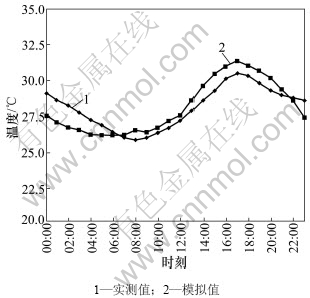
图4  室内空气温度的模拟值与实测值的对比

Fig.4  Comparison between simulated values and measured values of indoor air temperature

图5  室内空气的相对湿度实测值与模拟值的对比

Fig.5  Comparison between simulated values and measured values of indoor air relative humidity

3  结论

(1) 本文以Luikov多孔介质热湿耦合传递模型为基础，根据竹材组合墙体本身特点对模型进行合理简化，并确定简化模型的边界条件和初始条件。

(2) 根据长沙地区夏热冬冷的气候参数，利用Fluent软件对环境的温度、湿度进行模拟，并与实验实测值进行对比，对比结果显示模拟值与实测值吻合较好，误差在允许范围之内，误差应当是由实验中温度、湿度传感器的误差造成的，证明该数值模型具有较高的准确度。

(3) 在实验中还发现该种新型竹材组合墙体的热惰性大，蓄热能力强，隔热性能良好，因此可以在实际中推广应用。同时，在实际应用中利用本文数值模型对实际中建筑环境温度、湿度进行预测模拟，以达到更好的建筑节能效果和更舒适的建筑室内环境。

参考文献：

[1] Khsrow G. Bamboo as reinforcement in structural concrete elements[J]. Cement and Concrete Composites, 2005, 27(3): 637-649.

[2] 叶明, 钱城, 郝赤彪. 新型绿色建材—竹材人造板探讨[J]. 青岛理工大学学报, 2007, 28(5): 41-44.
YE Ming, QIAN Cheng, HAO Chi-biao. Bamboo-based panels as a new and green building material[J]. Journal of Qingdao Technological University, 2007, 28(5): 41-44.

[3] 张叶田, 岳慧. 竹材人造板—一种理想的工程结构材料[J]. 建筑知识, 2004(3): 17-18.
ZHANG Ye-tian, YUE Hui. Bamboo-based panel—A kind of ideal engineering structural material[J]. Architectural Knowledge, 2004(3): 17-18.

[4] 沈显超. 建筑围护结构防潮性能研究[D]. 武汉: 武汉理工大学, 2006: 1-2.
SHEN Xian-chao. Research on the damping proof performance of the building structure[D]. Wuhan: Wuhan University of Technology, 2006: 1-2.

[5] 李魁山, 张旭, 高军. 周期性边界条件下多层墙体内热湿耦合迁移[J]. 同济大学学报: 自然科学版, 2009, 27(6): 814-818.
LI Kui-shan, ZHANG Xu, GAO Jun. Coupled heat and moisture transfer in multi-wall under periodic boundary conditions[J]. Journal of Tongji University: Natural Science, 2009, 27(6): 814-818.

[6] Luikov A V. Systems of differential equations of heat and mass transfer in capillary-porous bodies[J]. International Journal of Heat and Mass Transfer, 1975(8): 1-14.

[7] Luikov A V. Heat and mass transfer[M]. Moscow: Mir, 1980.

[8] Thomas H R, Morgan K, Lewis R W. A fully nonlinear analysis of heat and mass transfer problems in porous media[J]. International Journal of Numerical Methods in Engineering, 1980, 15(9): 1381-1393.

[9] Lewis R W, Morgan K, Thomas H R. The finite element method in heat transfer analysis[M]. Chichester: John Wiley & Sons, 1996: 3-13.

[10] Younsi R, Kocaefe D, Kocaefe Y. Three-dimensional simulation of heat and moisture transfer in wood[J]. Applied Thermal Engineering, 2006, 26(11): 1274-1285.

[11] Liu J Y, Cheng S. Solution of Luikov equations of heat and mass transfer in capillary porous bodies[J]. International Journal of Heat and Mass Transfer, 1991, 34(7): 1747-1754.

[12] Malan A G, Lewis R W. Modeling coupled heat and mass transfer in drying non-hygroscopic capillary particulate materials[J]. Communication in Numerical Methods in Engineering, 2003, 19: 669-667.

[13] Scheerlinck N, Verboven P, Stigter J D, et al. A variance propagation algorithm for stochastic heat and mass transfer problems in food processes[J]. International Journal for Numerical Methods in Engineering, 2001, 51: 961-983.

[14] Dantas L B, Orlande H R B, Cotta R M. A inverse problem of parameter estimation for heat and mass transfer in capillary porous media[J]. International Journal of Heat and Mass transfer, 2003, 46: 1587-1598.

[15] Fluent Inc. Fluent 6.3 user’s guide[M]. 2006.

(编辑 杨华)

收稿日期：2012-01-15；修回日期：2012-02-15

基金项目：国家自然科学基金资助项目(50878078)

通信作者：李念平(1962-)，男，湖南邵阳人，教授，从事建筑节能与室内空气品质研究；电话：0731-88822610；E-mail: linianping@sina.com