不匹配不确定动态系统的鲁棒滑模观测器设计
申忠宇,赵瑾
(南京师范大学 电气与自动化工程学院,江苏 南京,210042)
摘要:研究不匹配不确定性动态系统的鲁棒滑模观测器设计问题。首先利用不匹配不确定性的滑模控制线性矩阵不等式(LMI)方法,提出不匹配不确定性的滑模观测器设计新方法以及非线性介入策略,通过Lyapunov函数证明观测器的稳定性和鲁棒性,使观测器的状态估计达到预期的指标;然后,给出滑模运动的稳定充分必要条件以及观测器的LMI存在定理,无须对动态系统进行规范化处理,将滑模观测器的综合设计归纳求解LMI问题,简化了设计过程。最后,通过数值仿真验证所提出方法的有效性。
关键词:滑模观测器;不匹配不确定系统;鲁棒性;线性矩阵不等式(LMI)
中图分类号:TP13 文献标志码:A 文章编号:1672-7207(2011)S1-0293-06
Robust sliding-mode observer design of
mismatched uncertain dynamic system
SHEN Zhong-yu, ZHAO Jin
(School of Electrical & Automation Engineering, Nanjing Normal University, Nanjing 210042, China)
Abstract: The robust sliding mode observer design is investigated for a class of uncertain dynamic system with mismatched uncertainties. First, a novel robust sliding mode observer design method and the nonlinear injection are proposed by using the sliding mode control approach for mismatched uncertainties based on linear matrix inequality (LMI). The Lyapunov function is used as the judgment condition for stabilizing observers so as to attain the desired performances of state estimation. Then, some sufficient and necessary conditions of stabilizing the sliding mode motion and the LMI existence theorem for observers are presented. Without the canonical transformation of the dynamic systems, a directly solvable LMI is obtained to release the constrained matrix equation causing the difficulty on synthesizing sliding mode observer, and the designing processes are simplified. Finally, the effectiveness of the proposed robust sliding mode observer design methodology is demonstrated through the numerical simulations.
Key words: sliding mode observer; mismatched uncertain system; robustness; linear matrix inequality (LMI)
滑模控制本质上是一类特殊的非线性控制,其非线性表现为控制的不连续,特别是滑模控制对匹配不确定具有良好的鲁棒性和灵敏性,在不确定动态系统得到广泛的研究和应用,近年来,滑模控制技术也被用来处理结构性和不匹配不确定的动态系统的控制及状态估计等研究。根据滑模控制理论,Utkin[1]提出线性系统的滑模观测器设计方法,利用等价控制原理使状态估计值与测量输出的误差在滑模面上从而减少测量误差;Walcott等[2]利用Lyapunov稳定性理论,结合滑模控制设计滑模观测器,但没有给出滑模观测器的增益矩阵的显式方式;Edwards等[3-5]在Walcott-Zak观测器的设计思想的基础上,提出规范化处理,使滑模观测器的矩阵方程转换为线性矩阵不等式,给出滑模观测器增益矩阵的显式方式,为滑模观测器设计问题建立一个可行性框架;接着一系列有关滑模观测器的设计原理以及方法的文献不断涌现[6-9]。然而,上述这些成果均未涉及不匹配不确定性动态系统,甚至系统矩阵的不确定情况。针对具有不匹配不确定动态系统,Choi等[10-12]利用滑模控制技术,提出了基于LMI的滑模切换面设计以及一系列设计框架。为此,本文作者针对一类不匹配不确定动态系统,将有关不匹配不确定性的变结构控制线性矩阵不等式LMI)设计方法[11],运用到鲁棒滑模观测器的设计中,提出了滑模观测 器的LMI存在定理以及稳定滑模运动的充分必要条件;无须对系统进行降阶处理或规范化处理,给出鲁棒滑模观测器综合设计的线性矩阵不等式求解构架,简化了设计步骤;通过数值仿真验证设计方法的可 靠性。
1 系统描述
考虑如下动态不确定系统[6]
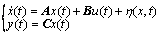 (1)
(1)
式中: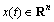 ;
; ;
;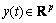 ;
;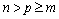 ,A, B和C为具有相应维数的矩阵;η(x, t)代表系统不确定因素、系统参数变化及外部干扰。不失一般性,假设如下条件成立。
,A, B和C为具有相应维数的矩阵;η(x, t)代表系统不确定因素、系统参数变化及外部干扰。不失一般性,假设如下条件成立。
(A1) η(x, t)满足下列条件:
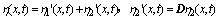

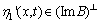 (2)
(2)
η1′(x, t)不满足匹配条件,η2′(x, t)满足匹配条件,且η2(x, t)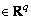 ,
,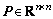 对称正定矩阵。存在某一非负函数
对称正定矩阵。存在某一非负函数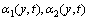 ,使得
,使得
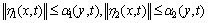 。
。
(A2) (A, C)可观,即存在矩阵G,使矩阵A-GC的特征值在左半平面。
(A3) 矩阵D和C满秩,且rank(CD)=q
由此可见,动态不确定系统(1)可以写成下列形式:

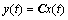 (3)
(3)
则问题归结为对动态系统(3)的鲁棒滑模观测器的设计,选择合适的增益矩阵以及非线性介入量使观测误差趋向于0。
引理1[6]:对于任意正定矩阵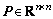 和
和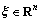 ,有
,有

其中: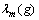 和
和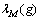 分别代表矩阵P的最小、最大特征值。
分别代表矩阵P的最小、最大特征值。
2 基于LMI的鲁棒滑模观测器设计
考虑不匹配不确定性的动态不确定系统(3),本文设计滑模观测器的形式:
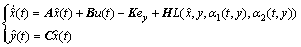 (4)
(4)
其中: 为观测器的估计状态;
为观测器的估计状态;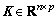 为滑模观测器的增益矩阵;
为滑模观测器的增益矩阵;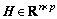 为设计参数矩阵,满足rank(CH)=p;
为设计参数矩阵,满足rank(CH)=p;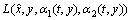 为依赖于系统不确定性η(x, t)的非线性介入量,又称
为依赖于系统不确定性η(x, t)的非线性介入量,又称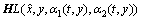 为非线性介入量。定义观测状态误差向量和输出误差向量分别为:
为非线性介入量。定义观测状态误差向量和输出误差向量分别为:
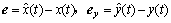 (5)
(5)
定理1 对不匹配不确定性的动态不确定系统(3),当满足假设条件(A1)~(A3),且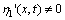 时,设计的滑模观测器见式(4),同时非线性介入
时,设计的滑模观测器见式(4),同时非线性介入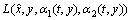 定义为
定义为
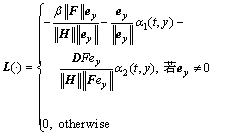 (6)
(6)
其中:β由系统不确定因素确定。则设计的滑模观测器具有较强的鲁棒性,以及一致最终有界的构造误差,其误差界为
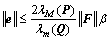
证明:根据状态估计误差(5),则其微分方程为
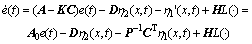 (7)
(7)
式中: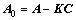 ,使
,使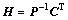 。定义Lyapunov方程
。定义Lyapunov方程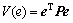 ,则
,则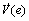 为
为


若假设条件(A3)成立,则观测器的增益矩阵K满足:

同时,由假设条件(A1),则上式可以写成下列形式:




根据引理1,上式可以写成:

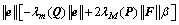
要使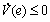 ,则
,则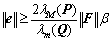 ,所以,设计的滑模观测器对系统不确定具有鲁棒性,同时,具有一致最终有界的构造误差,即
,所以,设计的滑模观测器对系统不确定具有鲁棒性,同时,具有一致最终有界的构造误差,即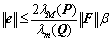 。证毕。
。证毕。
根据不匹配不确定性的动态系统变结构控制LMI设计原理[10-11],提出鲁棒滑模观测器的LMI存在条件,确保在切换平面上的稳定滑模运动。
定理2 观测误差系统(7)在切换平面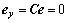 存在稳定的滑模运动以及对系统的不确定性具有鲁棒性的充分必要条件是,存在正定对称矩阵
存在稳定的滑模运动以及对系统的不确定性具有鲁棒性的充分必要条件是,存在正定对称矩阵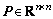 满足
满足
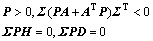 (8)
(8)
其中: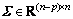 是矩阵C的正交补矩阵。
是矩阵C的正交补矩阵。
证明:充分性。若条件(8)存在,则使设计参数矩阵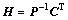 ,则定义非奇异变换矩阵
,则定义非奇异变换矩阵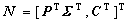 以及向量
以及向量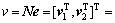
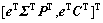 。可以看出:
。可以看出: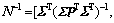
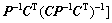 ,且
,且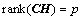 ;同时,
;同时,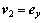 。将它们代入式(7),形成规范形式:
。将它们代入式(7),形成规范形式:

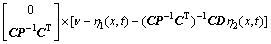 (9)
(9)
其中:
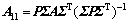 ;
;
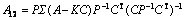 ;
;
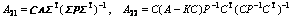 。
。
根据滑模观测器等价输出控制理论,当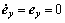 时,则系统的动态特性表现为
时,则系统的动态特性表现为
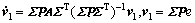 (10)
(10)
由此可见:滑模动态特性稳定的充分必要条件是存在正定的Lyapunov矩阵Q0满足
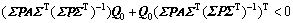
从条件(8)可以看出:当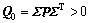 时上式成立。
时上式成立。
必要性:构造满秩矩阵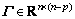 ,使得
,使得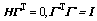 ;引入非奇异变换矩阵
;引入非奇异变换矩阵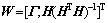 ,
,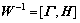 ,对误差系统进行非奇异变换处理,新的坐标
,对误差系统进行非奇异变换处理,新的坐标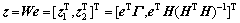 ,误差系统(7)变成下列规范形式:
,误差系统(7)变成下列规范形式:
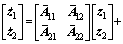
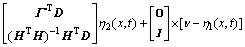
其中:
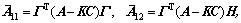


假设在切换平面上存在滑模运动,即: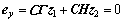 。由等价输出控制理论则
。由等价输出控制理论则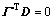 ,滑模动态特性为
,滑模动态特性为
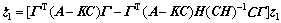 (11)
(11)
当约束Riccati方程对(P, F)有可行性解,则滑模动态特性稳定。
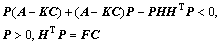
因为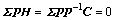 ,上述约束的Riccati方程写成:
,上述约束的Riccati方程写成:

而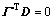 意味着存在矩阵
意味着存在矩阵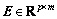 满足D=HE,使等式
满足D=HE,使等式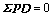 成立。
成立。
证毕。
但是定理2给出的条件(8)不能直接用来计算滑模观测器的增益矩阵和其他设计矩阵如K, H和F, 由此提出滑模观测器的LMI存在条件,这里只给出定理,定理的证明略去。
定理3 存在正定矩阵P满足式(8)充分必要条件是:对称矩阵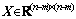 ,
,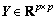 和矩阵
和矩阵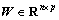 使得下列LMI条件具有可行性解:
使得下列LMI条件具有可行性解:
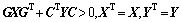
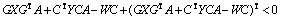 (12)
(12)
其中: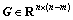 是矩阵D的正交补矩阵。因此,可以得到正定矩阵P和设计矩阵L,H和F的解:
是矩阵D的正交补矩阵。因此,可以得到正定矩阵P和设计矩阵L,H和F的解:

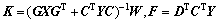 (13)
(13)
备注1:由于矩阵X作为线性矩阵不等式的可行性解,因此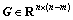 作为矩阵D的正交补矩阵,可以通过多种选择方法获取。
作为矩阵D的正交补矩阵,可以通过多种选择方法获取。
备注2:式(12)是标准的LMIs,因此,通过MATLAB的LMI工具箱,直接利用包含在式(12)的系统参数进行求解,得到其LMIs的可行性解(X, Y, W),无须对系统进行规范化处理,简化了鲁棒滑模观测器的设计过程。
备注3:定理3作为滑模观测器的LMI存在条件,给出一个简单易处理LMI的判断原则。
备注4:若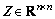 为对称正定矩阵,则利用Schur分解不等式
为对称正定矩阵,则利用Schur分解不等式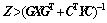 ,得到线性矩阵不等式:
,得到线性矩阵不等式:
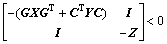 (14)
(14)
由此可见:对线性矩阵不等式的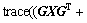
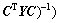 ,最小化问题等价为这些线性矩阵不等式的
,最小化问题等价为这些线性矩阵不等式的
trace(Z)最小化问题,因此,可以将对线性矩阵不等式的可行性问题化为具有线性矩阵不等式约束最小化 问题。
备注5:利用MATLAB的LMI工具箱中的约束的凸优化问题求解器mincx(·),得到滑模观测器的增益矩阵和设计矩阵。
3 数值举例
根据文献[12]提供的5阶动态不确定系统,满足匹配条件的不确定项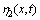 ,不满足匹配条件的不确定项
,不满足匹配条件的不确定项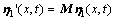 ,并设定
,并设定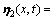
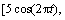
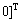 和
和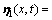
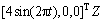 ;且系统状态矩阵A, B, D和C分别为:
;且系统状态矩阵A, B, D和C分别为:
 ,
,
 ,
,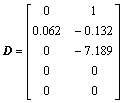 ,
,
 (15)
(15)
滑模观测器的优化滑模策略由下式近似:
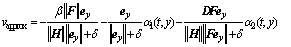 (16)
(16)
式中: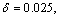
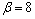 ,
, 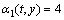 和
和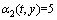 。
。
设定系统状态初值和滑模观测器估计状态初 值为:
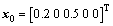 和
和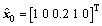 ,此外系统状态
,此外系统状态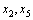 状态可测无须估计。
状态可测无须估计。
根据定理3以及MATLAB的LMI工具箱,求解优化问题(12)和(14),以及计算滑模观测器的矩阵(13)得到:





为了很好地显示所设计的鲁棒滑模观测器的 效果,分为2组进行滑模观测器的仿真验算,第1组为:
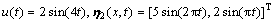 ,
,
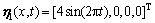 (17)
(17)
第2组为:
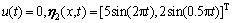 ,
,
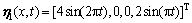 (18)
(18)
这里只给出状态x3和x4仿真曲线,图1和图2所示分别为在条件(17)和(18)下比较鲁棒滑模观测器的估计状态与系统状态仿真结果图。从图1和图2可以看出:设计的鲁棒滑模观测器具有比较好的跟踪性能以及鲁棒性。
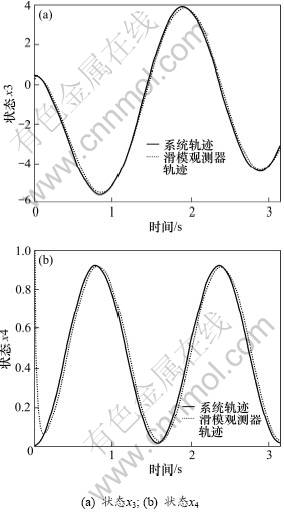
图1 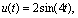
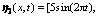
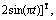
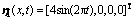 下系统和观测器的轨迹
下系统和观测器的轨迹
Fig.1 Trajectories of system states x and sliding mode observer states  in
in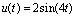 ,
, 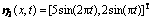 and
and 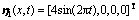
4 结论
针对一类不匹配不确定的动态系统,给出了鲁棒滑模观测器设计的新方法,该方法的特点主要体现在3个方面,一是无须对系统进行规范化处理,简化了鲁棒滑模观测器设计过程,利用滑模控制理论针对同时存在匹配和不匹配不确定使观测器具有鲁棒性;二是给出滑模观测器的线性矩阵不等式存在定理以及相关理论证明;三是将滑模观测器的综合设计问题转换为直接求解线性矩阵不等式问题。最后,通过数值仿真例子验证所提设计方法的有效性,同时,本文所提出的滑模观测器设计方法已经应用于一类不匹配不确定系统的鲁棒故障重构中。
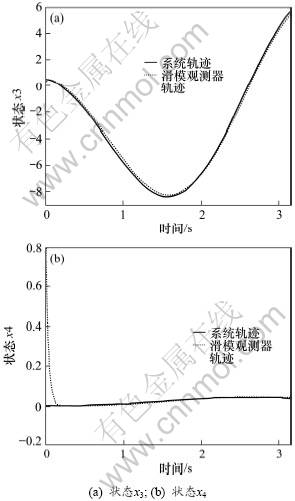
图2 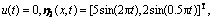

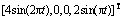 下系统和观测器的轨迹
下系统和观测器的轨迹
Fig.2 Trajectories of system states x and sliding mode observer states  in
in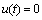 ,
, 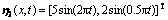 and
and 
参考文献:
[1] Utkin V. Sliding modes in control optimization [M]. New York: Springer Verlag, 1992: 234-560.
[2] Walcott B, Zak S H. Combined observer-controller synthesis for uncertain dynamical systems with applications [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1988, 18(1): 88-104.
[3] Edwards C, Spurgeon S K. On the development of discontinuous observers [J]. International Journal of Control, 1994, 59(5): 1211-1229.
[4] Tan P C, Edwards C. An LMI approach for designing sliding mode observers [J].International Journal of Control, 2001, 74(16): 1559-1568.
[5] Floquet T, Edwards C, Spurgeon S K. On sliding mode observers for systems with unknown inputs [J]. International Journal of Adaptive Control and Signal Processing, 2007, 21(1): 638-656.
[6] 王江, 王先来, 王海涛. 非线性变结构观测器[J]. 控制理论与应用, 1997, 14(4): 603-607
WANG Jiang, WANG Xian-lai, WANG Hai-tao. Variable structure observer of non-linear control systems[J]. Control Theory and Applications. 1997, 14(4): 603-607
[7] Zheng Y H, Fattah H A, Loparo K A. Non-linear adaptive sliding mode observer-controller scheme for induction motors[J]. International Journal of Adaptive Control and Signal Processing, 2000, 14(2): 245-273.
[8] 赵瑾, 顾幸生, 申忠宇. 线性不确定系统的鲁棒滑模观测器设计与仿真[J]. 华东理工大学学报: 自然科学版, 2006, 32(7): 810-813.
ZHAO Jin, GU Xin-sheng, SHEN Zhong-yu. Robust sliding mode observer design and simulation for linear uncertain systems [J]. Journal of East China University of Science & Technology: Natural Science Edition, 2006, 32(7): 810-813.
[9] 项基, 苏宏业, 褚健. 一类不确定系统的滑模观测器设计[J]. 控制理论与应用, 2006, 23(6): 996-1000, 1004.
XIANG Ji, SU Hong-ye, CHU Jian. Sliding mode observer design for a class of uncertain systems[J]. Control Theory and Applications, 2006, 23(6): 996-1000, 1004.
[10] Choi H H. On the existence of linear sliding surfaces for a class of uncertain dynamic systems with mismatched uncertainties[J]. Automatica, 1999, 35(10): 1707-1715.
[11] Choi H H. An LMI-based switching surface design method for a class of mismatched uncertain systems[J]. IEEE Transactions on Automatic Control, 2003, 48(9): 1634-1638.
[12] Xiong Y, Saif M. Unknown disturbance inputs estimation based on a state functional observer design[J]. Automatica, 2003, 39(12): 1389-1398.
(编辑 杨幼平)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(61074024);江苏省高校自然科学基础研究面上资助项目(09KJB510005)
通信作者:申忠宇(1962-),男,江苏靖江人,教授,从事故障检测与诊断、智能控制研究。电话:025-85481039; E-mail: shenzhongyu@njnu.edu.cn