文章编号:1004-0609(2011)10-2489-13
FP-SSA框架中Au3Cu型有序合金相的
特征原子势能配分函数
谢佑卿1, 2,聂耀庄3,李小波4,刘心笔1, 2,彭红建5,李艳芬1, 2
(1. 中南大学 材料科学与研究工程学院,长沙 410083;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083;
3. 中南大学 物理科学与技术学院,长沙 410083;
4. 湘潭大学 机械工程学院,湘潭 411105;
5. 中南大学 化学化工学院,长沙 410083)
摘 要:介绍以第一原理合金电子理论为基础的系统合金科学(FP-SSA)框架中Au3Cu型有序合金的特征原子势能(CAPE)配分函数。主要创新内容如下:以基本原子团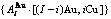 和
和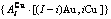 序列的中心特征原子
序列的中心特征原子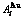 和
和 为结构单元序列,替代原子对和原子团,建立了合金相的特征原子排列模型;以配位原子团
为结构单元序列,替代原子对和原子团,建立了合金相的特征原子排列模型;以配位原子团 对作用于特征原子势场影响的方式替代原子对能量相互作用和原子团能量相互作用方式,以特征原子势能能级代替原子对能级和原子团能级,建立了合金相的“特征原子势能相加定律”,计算合金相及其组元的平均势能;在特征原子排列的简并因数与特征原子势能能级一致的条件下建立CAPE配分函数和计算组态熵。此函数揭示了当今流行的固溶体理论的不足之处,为建立特征Gibbs能配分函数奠定了基础。
对作用于特征原子势场影响的方式替代原子对能量相互作用和原子团能量相互作用方式,以特征原子势能能级代替原子对能级和原子团能级,建立了合金相的“特征原子势能相加定律”,计算合金相及其组元的平均势能;在特征原子排列的简并因数与特征原子势能能级一致的条件下建立CAPE配分函数和计算组态熵。此函数揭示了当今流行的固溶体理论的不足之处,为建立特征Gibbs能配分函数奠定了基础。
关键词:Au3Cu型有序合金;第一原理;系统合金科学;特征原子;势能;配分函数
中图分类号:TG131 文献标志码:A
Characteristic atom potential energy partition function of Au3Cu type ordered alloys in FP-SSA framework
XIE You-qing1, 2, NIE Yao-zhuang3, LI Xiao-bo4, LIU Xin-bi1, 2, PENG Hong-jian5, LI Yan-fen 1, 2
(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
3. School of Physical Science and Technique, Central South University, Changsha 410083, China;
4. College of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China;
5. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China)
Abstract: The innovations of the characteristic atom potential energy (CAPE) partition function of Au3Cu type ordered alloys in the systematic science of alloys (SSA) based on first principle (FP)-electronic theory of alloys are concluded in the three aspects: the characteristic atoms 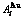 and
and  at centers of the basic clusters
at centers of the basic clusters 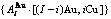 and
and 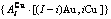 are taken as structural unit sequences, which are used to replace the atomic pairs and atomic clusters; the potential energy levels
are taken as structural unit sequences, which are used to replace the atomic pairs and atomic clusters; the potential energy levels 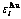 and
and 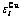 result from the influence of coordinative cluster
result from the influence of coordinative cluster 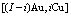 on the characteristic atoms, which are used to replace pairwise interaction energies and cluster interaction energies; the additive law of potential energies of characteristic atoms is established; the average potential energies of alloy phases and their components are calculated; the unity between the degeneracy factors of arrangements and the potential energy levels of characteristic atoms is taken into account for establishing CAPE-partition function and calculating configurational entropy. It reveals some shortcomings of the currently used solution theories and can lay the foundation for establishing Gibbs energy partition function.
on the characteristic atoms, which are used to replace pairwise interaction energies and cluster interaction energies; the additive law of potential energies of characteristic atoms is established; the average potential energies of alloy phases and their components are calculated; the unity between the degeneracy factors of arrangements and the potential energy levels of characteristic atoms is taken into account for establishing CAPE-partition function and calculating configurational entropy. It reveals some shortcomings of the currently used solution theories and can lay the foundation for establishing Gibbs energy partition function.
Key words: Au3Cu-type ordered alloys; the first principle; systematic science of alloys; characteristic atom; potential energy; partition function
依据一般系统科学的3个哲学命题,建立了系统合金科学(SSA)框架。这3个命题是:1) 任何一个系统中其结构的多样性归因于结构单元序列中结构单元的组合和排列;2) 系统的性质多样性归因于结构单元之间的相互作用内容和方式;3) 多组元系统的复杂性和整体性归因于结构和性质的多层次性,不同结构层次之间的相关性以及系统与环境合一的开放性。
SSA框架包含两部分:SSA理论框架和合金特征原子排列设计应用工程。SSA理论框架分为两个分 支:以第一原理(FP)——合金电子理论和以实验测量技术(EX)为基础的SSA理论框架。它包含6个彼此相关联的层次理论(见图1)[1],它们之间的关系用结构单元序列链、公式链和信息链描述。其目的之一是阐明合金系统3个结构层次的结构和性质的多样性。这3
个结构层次是:1) 组织结构,组成单元为相;2) 合金相结构,组成单元为原子;3) 合金相中原子的电子结构,组成单元为电子和原子核。
合金相是组元原子在基本点阵中排列的溶体。发展SSA框架中的合金相溶体理论就是要按照系统科学的3个哲学命题在相应的3个方面创新,建立配分函数,然后导出系列公式,如Gibbs能函数等。对于单相j的溶体,有
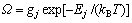 (1)
(1)
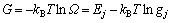 (2)
(2)
式中: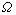 为势能配分函数;gj为原子排列简并因数;Ej为合金能量状态;kB为Baltzman常数;T为热力学温度;G为Gibbs自由能。
为势能配分函数;gj为原子排列简并因数;Ej为合金能量状态;kB为Baltzman常数;T为热力学温度;G为Gibbs自由能。
这3个方面是:1) 寻找能够阐明合金相结构多样性的结构单元序列,建立结构模型;2) 选择能量相互作用方式,确定组元( )的结构单元能级(
)的结构单元能级( )和相应的原子浓度(
)和相应的原子浓度( );3) 建立与合金相能量状态
);3) 建立与合金相能量状态 (Ej=
(Ej=
 )相应的原子排列简并因数
)相应的原子排列简并因数 和熵
和熵
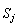 (
(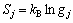 )的计算方法。
)的计算方法。
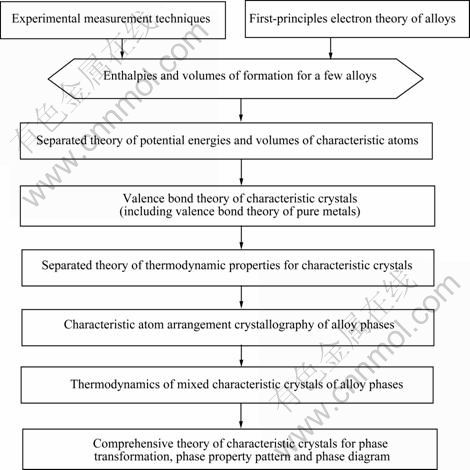
图1 以实验技术和第一原理金属间化合物电子理论为基础的SSA理论框架的层次理论
Fig.1 Theoretical levels of SSA framework based on experimental measurement techniques and first principle electron theory of alloys
配分函数是相结构层次公式链中的基本函数。CAPE配分函数的建立,不仅能为建立特征原子Gibbs能配分函数奠定基础,而且能揭示当今流行的相图计算(CALPHAD)评估[2]和它与原子集团变分法(CVM)[3]结合的CALPHD-CVM理论[4]以及FP-电子结构计算与CVM法结合的FP-CVM理论[5]的不足之处。它们是过去20多年来正在形成的新方向,这是因为在高温下组态熵对合金相的Gibbs能起重要作用[6]。
本文作者将以Au3Cu型有序合金为例,介绍CAPE配分函数、特征原子浓度分布函数、特征原子势能分布函数以及与特征原子能级相应的原子排列简并因数,计算合金相及其组元的平均原子势能、摩尔生成焓和摩尔组态熵。
1 结构单元和结构单元的势能能级
在FCC基本格子Au-Cu系中,每个原子受最近邻配位原子团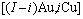 包围,这里,i是Cu原子数,(I-i)是Au原子数,I是配位数,其值等于12。因此, 能够描述合金相中原子空间排列的几何特征和原子之间相互作用方式的结构单元是基本原子团
包围,这里,i是Cu原子数,(I-i)是Au原子数,I是配位数,其值等于12。因此, 能够描述合金相中原子空间排列的几何特征和原子之间相互作用方式的结构单元是基本原子团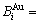
 和
和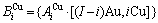 。
。
在L12-Au3Cu化合物中,每个Au原子(称为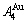 特征原子)由配位原子团[8Au, 4Cu]包围,每个Cu原子(称之为
特征原子)由配位原子团[8Au, 4Cu]包围,每个Cu原子(称之为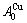 特征原子)由配位原子团[12Au, 0Cu]包围。L12-Au3Cu的FCC基本格子由两个亚点阵组合形成,一个由
特征原子)由配位原子团[12Au, 0Cu]包围。L12-Au3Cu的FCC基本格子由两个亚点阵组合形成,一个由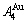 原子占据,另一个由
原子占据,另一个由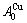 原子占据(见图2)。当L12-Au3Cu变成Au0.75Cu0.25无序合金时,基本原子团
原子占据(见图2)。当L12-Au3Cu变成Au0.75Cu0.25无序合金时,基本原子团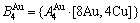 和
和 分裂成为
分裂成为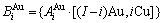 和
和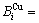
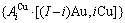 序列。由于配位原子团[8Au, 4Cu]和[12Au, 0Cu]分裂成配位原子团
序列。由于配位原子团[8Au, 4Cu]和[12Au, 0Cu]分裂成配位原子团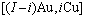 序列,导致作用于
序列,导致作用于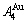 和
和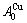 特征原子的势场发生变化;特征原子
特征原子的势场发生变化;特征原子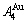 和
和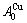 分裂成
分裂成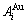 和
和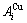 特征原子序列,它们的势能
特征原子序列,它们的势能 和
和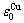 分裂成
分裂成 和
和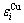 序列,体积
序列,体积 和
和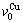 分裂成
分裂成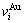 和
和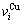 序列。
序列。
根据这一分析, 本文作者提出了阐明合金相结构和性质多样性的3个相互关联的模型[7-11]:1) 基本原子团交叠(BCO)模型,合金相由基本原子团交叠形成,其结构单元为一对基本原子团 和
和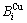 序列;2) 特征原子排列(CAA)模型,合金相由特征原子排列形成,其结构单元为一对特征原子
序列;2) 特征原子排列(CAA)模型,合金相由特征原子排列形成,其结构单元为一对特征原子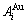 和
和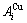 序列;3) 特征晶体混合(CCM)模型,合金相由特征晶体混合形成,其结构单元是特征原子组成的
序列;3) 特征晶体混合(CCM)模型,合金相由特征晶体混合形成,其结构单元是特征原子组成的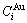 和
和 序列。此模型是缘于以下启示提出的:纯金属FCC-Au和FCC-Cu是Au-Cu系中的子系统,它们分别由Au-Cu系中特征原子
序列。此模型是缘于以下启示提出的:纯金属FCC-Au和FCC-Cu是Au-Cu系中的子系统,它们分别由Au-Cu系中特征原子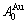 和
和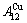 排列形成的特征晶体
排列形成的特征晶体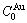 和
和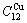 。因此,13种
。因此,13种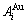 和
和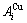 特征原子可分别形成13种虚拟的
特征原子可分别形成13种虚拟的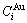 特征晶体和13种虚拟的
特征晶体和13种虚拟的 特征晶体。
特征晶体。
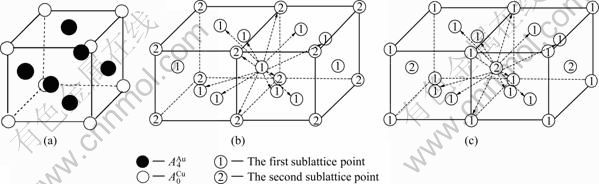
图2 L12-Au3Cu化合物特征原子排列晶体结构、以第一类亚格点为中心的最近邻配位格点及以第二类亚格点为中心的最近邻配位格点
Fig.2 Characteristic atom occupation structure of L12-Au3Cu compound (a), the first and second sublattice points in coordinative cluster surrounding the first sublattice point (b), and the first and second sublattice points in coordinative cluster surrounding the second sublattice point (c)
为了计算Au-Cu系中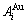 和
和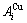 特征原子序列的
特征原子序列的 和
和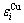 势能序列,首先采用LDA近似(Local density approximation)的PAW (Projector augmented wave)法计算了L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及纯Au和纯Cu的结合能和生成焓。由此法计算的结果与OZOLIN?等[12]的结果相近,但都与实验值有较大偏差。这是因为没有考虑相对论效应,而此效应对Au元素影响较大。随后,采用SRA近似(Scalar relativistic approximation) 的PWP(Plane wave pseudopotential)法进行计算,其结果与实验值偏差减小。最后,考虑自旋即轨道-轨道耦合(SO),由PWP+ SO方法计算得到的生成焓与实验值吻合较好(见表1)。
势能序列,首先采用LDA近似(Local density approximation)的PAW (Projector augmented wave)法计算了L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及纯Au和纯Cu的结合能和生成焓。由此法计算的结果与OZOLIN?等[12]的结果相近,但都与实验值有较大偏差。这是因为没有考虑相对论效应,而此效应对Au元素影响较大。随后,采用SRA近似(Scalar relativistic approximation) 的PWP(Plane wave pseudopotential)法进行计算,其结果与实验值偏差减小。最后,考虑自旋即轨道-轨道耦合(SO),由PWP+ SO方法计算得到的生成焓与实验值吻合较好(见表1)。
为了从第一原理计算的化合物生成焓中分离出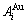 和
和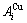 特征原子势能
特征原子势能 和
和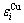 序列,采用“结构单元反算法”。它类似于FP-CVM框架求解有效原子团相互作用参数。此方法采用由初态(纯金属)和末态特征原子势能(
序列,采用“结构单元反算法”。它类似于FP-CVM框架求解有效原子团相互作用参数。此方法采用由初态(纯金属)和末态特征原子势能(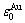 和
和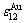 ,
, 和
和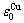 )描述的合金平均原子势能(T=0 K)与成分(x)和有序度(
)描述的合金平均原子势能(T=0 K)与成分(x)和有序度(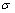 )关系的9个函数[10](列于表2)。这9个函数分别由如下3种标 准
)关系的9个函数[10](列于表2)。这9个函数分别由如下3种标 准 函数组合形成:
函数组合形成:
表1 0 K时采用第一原理计算的L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及纯Au和纯Cu的生成焓、结合能及其实验值
Table 1 Heats of formation (?h) and cohesive energies (Ec) of L10-AuCu, L12-Au3Cu and L12-AuCu3 compounds, Au, and Cu metals at 0 K calculated by FP-electron theory and measured by experimental techniques
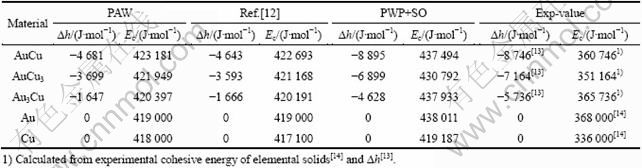
表2 合金的平均原子势能函数
Table 2 Average atomic potential energy functions of alloy phases

1) 直线关系(Ⅰ型)
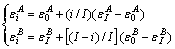 (3)
(3)
2) 凹型抛物线关系(Ⅱ型)
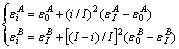 (4)
(4)
3) 凸型抛物线关系(Ⅲ型)
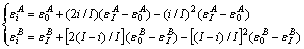 (5)
(5)
按以下步骤分离出Au-Cu系中特征原子势能:
1) 采用结构单元反算法,应用9个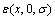 函数从第一原理计算的L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及纯Au和纯Cu的总势能中分离出特征原子势能。
函数从第一原理计算的L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及纯Au和纯Cu的总势能中分离出特征原子势能。
2) 由9个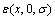 函数和相应的特征原子势能计算最大有序度Au3Cu、AuCu和Au3Cu型有序合金,无序合金的生成焓,以及它们的差值(即过剩势能)。
函数和相应的特征原子势能计算最大有序度Au3Cu、AuCu和Au3Cu型有序合金,无序合金的生成焓,以及它们的差值(即过剩势能)。
3) 在不考虑振动对焓和熵的贡献,且假设合金的最大有序度(计算公式见第3节)不随温度变化的情况下,由式(6)计算有序-无序转变临界温度Tc:
 (6)
(6)
计算结果表明, 由第5E函数获得的Tc温度较其他E函数获得的Tc温度更接近实验值(见图3)。与此函数对应的特征原子势能之间的关系为
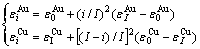 (7)
(7)
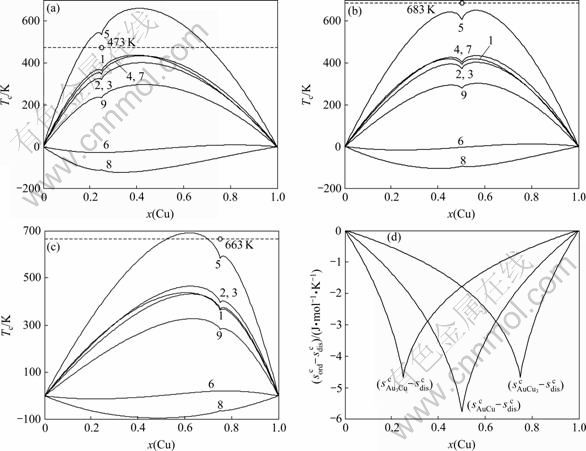
图3 最大有序度Au3Cu、AuCu和Au3Cu型合金有序-无序转变临界温度和熵差值
Fig.3 Critical temperatures Tc ((a), (b), (c)) and configurational entropies sc(x, σmax) differences (d) of Au3Cu- (a), AuCu- (b) and AuCu3- (c) type ordered alloys with maximum ordering degrees relative to disordered Au(1-x)Cux alloys (Dotted lines are experimental critical temperatures Tc of Au3Cu, AuCu and AuCu3 compounds)
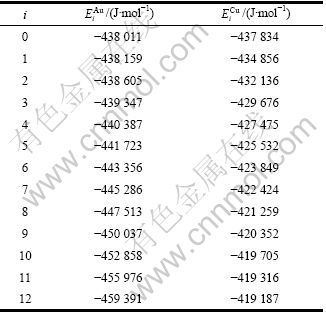
Au-Cu系中特征原子的势能列于表3[1]。它们属于Au-Cu系的能级,适用于所有合金相:Au3Cu、AuCu和AuCu3化合物,成分可变的Au3Cu、AuCu和AuCu3型有序合金以及无序Au(1-x)Cux合金。
表3 Au-Cu系中特征原子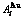 和
和 的摩尔势能
的摩尔势能
Table 3 Potential energies of 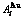 and
and  characteristic atoms in Au-Cu system
characteristic atoms in Au-Cu system
2 Au3Cu型有序合金相的CAPE配分函数公式链
公式链表明,CAA模型本质上等同于Bragg- Williams模型[15]和中心原子模型[16]的组合。CAPE配分函数考虑了特征原子的势能能级和原子排列简并因子之间的一致性。
1) CAPE配分函数
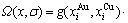
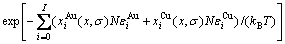 (8)
(8)
2) 简并因数函数
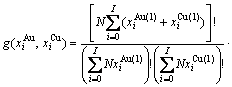
 (9)
(9)
3) 组态熵函数
 (10)
(10)
4) 特征原子浓度分布函数
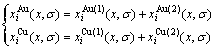 (11)
(11)
5) 占居第(1)和第(2)亚格点的特征原子浓度
 (12)
(12)
6) Au和Cu原子占居第(1)和第(2)亚格点概率
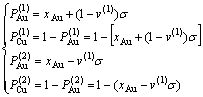 (13)
(13)
7) Au3Cu型有序合金的第(1)和第(2)亚格点分数
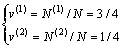 (14)
(14)
8) 有序度的定义
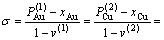
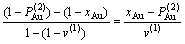 (15)
(15)
9) 围绕第(1)亚格点的配位原子团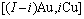 的概率
的概率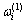
 (16)
(16)
式中: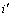 是占居第(1)亚格点上Cu原子数;
是占居第(1)亚格点上Cu原子数;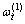 是占居第(1)亚格点的配位原子团
是占居第(1)亚格点的配位原子团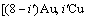 的概率;
的概率;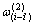 是占居第(2)亚格点的配位原子团
是占居第(2)亚格点的配位原子团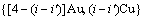 的概率。
的概率。
10) 围绕第(2)亚格点的配位原子团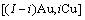 的概率
的概率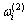
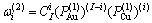 (17)
(17)
式(16)和(17)中,k和K按下列规则取值:
 (18)
(18)
11) Au3Cu型有序合金最大有序度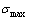 与组元浓度的关系由式(15)得到:
与组元浓度的关系由式(15)得到:
对于化学计量比合金,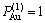 ,
, =1;
=1;
对于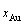 <
< 的合金,
的合金,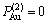 ,
,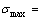
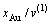 ;
;
对于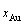 >
> 的合金,
的合金,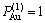 ,
,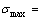
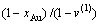 。
。
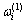 和
和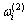 计算方法列于表4和5。
计算方法列于表4和5。
12) 合金和组元的平均势能(特征原子势能相加定律)
 (19)
(19)
13) 0 K时合金和组元的平均生成焓
 (20)
(20)
式(19)和(20)表明,Au组元和Cu组元的平均原子势能( ,
,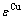 )和生成焓(
)和生成焓(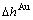 ,
,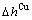 )可直接获得。而在传统溶体理论中,组元的平均性质是由偏摩尔性质理论间接获得,而这已证明是不正确的[1]。
)可直接获得。而在传统溶体理论中,组元的平均性质是由偏摩尔性质理论间接获得,而这已证明是不正确的[1]。
应当指出的是,特征原子Gibbs能(CAGE)配分函数已经建立,但建立和说明它并不容易。
3 结果
应用CAPE配分函数,计算Au3Cu型有序合金Au(1-x)Cux的特征原子浓度 和
和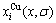 在势能能级上的能级分布、特征原子势能分布、合金及组元的势能、生成焓和组态熵随成分和有序度的变化,结果如图4~8所示。
在势能能级上的能级分布、特征原子势能分布、合金及组元的势能、生成焓和组态熵随成分和有序度的变化,结果如图4~8所示。
结果表明,CAPE配分函数考虑了特征原子的势能能级和原子排列简并因子之间的一致性,并且组元的平均势能和平均生成焓不必采用偏摩尔性质理论可以直接得到。
4 讨论
由特征原子势能可建立由“特征原子对键能”描述的合金摩尔势能公式:

 (21)
(21)
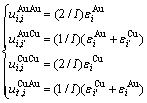 (22)
(22)
式中: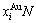 和
和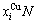 分别为
分别为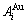 和
和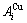 的特征原子数
的特征原子数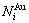 和
和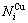 ;
;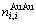 和
和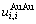 分别为
分别为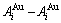 原子对数和键能;
原子对数和键能;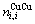 和
和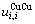 分别为
分别为 原子对数和键能;
原子对数和键能; 和
和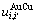 分别为
分别为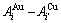 原子对数和键能。
原子对数和键能。
由L12-Au3Cu化合物中的摩尔势能、特征原子势能和特征原子对键能的关系可证明式(21)等同于式(19):
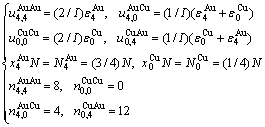 (23)
(23)
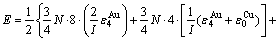
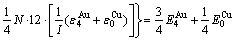 (24)
(24)
表4 Au3Cu型有序合金中,围绕第(1)亚格点的配位原子团[(I-i)Au, iCu]的概率 的计算方法
的计算方法
Table 4 Methods for calculating probability  of coordinative cluster [(I-i)Au, iCu] surrounding (1)-sublattice point in Au3Cu-type ordered alloys
of coordinative cluster [(I-i)Au, iCu] surrounding (1)-sublattice point in Au3Cu-type ordered alloys
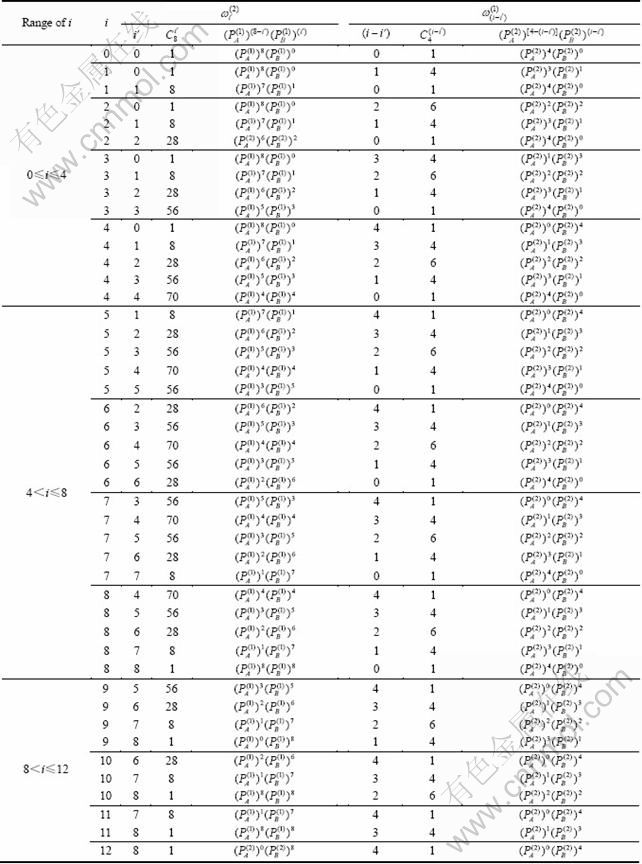
表5 Au3Cu型有序合金中围绕第(2)亚格点的配位原子团[(I-i)Au, iCu]概率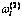 的计算方法
的计算方法
Table 5 Methods for calculating probability 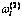 of coordinative cluster [(I-i)Au, iCu] surrounding (2)-sublattice point in Au3Cu-type ordered alloys
of coordinative cluster [(I-i)Au, iCu] surrounding (2)-sublattice point in Au3Cu-type ordered alloys
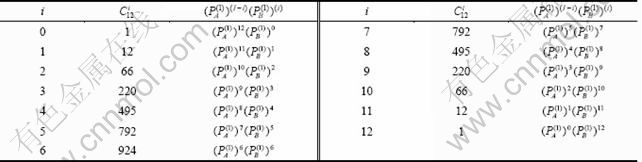
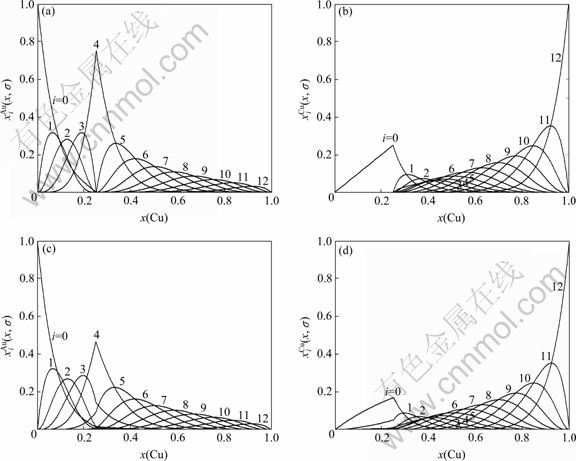
图4 Au3Cu型有序合金Au(1-x)Cux的特征原子浓度 和
和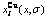 的分布
的分布
Fig.4 Concentrational  and
and 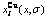 distributions of characteristic atoms in Au3Cu-type ordered Au(1-x)Cux alloys corresponding to potential energy levels: (a)
distributions of characteristic atoms in Au3Cu-type ordered Au(1-x)Cux alloys corresponding to potential energy levels: (a) , σ=σmax; (b)
, σ=σmax; (b)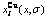 , σ=σmax; (c)
, σ=σmax; (c) , σ=0.9σmax; (d)
, σ=0.9σmax; (d)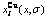 , σ=0.9σmax
, σ=0.9σmax
假设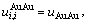
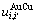 =
=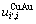 =
=
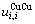 =
=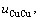 则式(21)简化为Bragg-Williams近似[15] 的合金摩尔势能与原子对键能的关系式:
则式(21)简化为Bragg-Williams近似[15] 的合金摩尔势能与原子对键能的关系式:
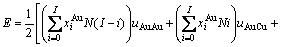
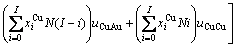 (25)
(25)
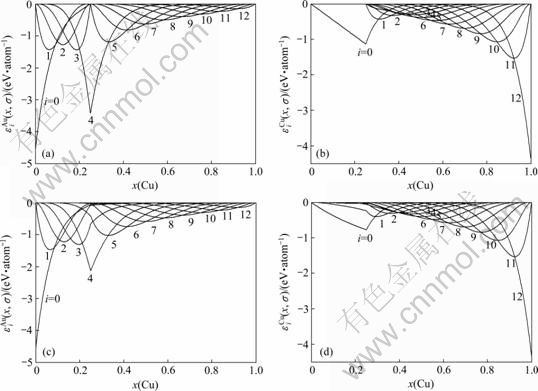
图5 Au3Cu型有序合金Au(1-x)Cux中对应于势能能级的势能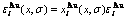 和
和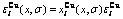 的分布
的分布
Fig.5 Potential energy 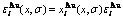 and
and 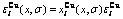 distributions of characteristic atoms in Au3Cu-type ordered Au(1-x)Cux alloys corresponding to potential energy levels: (a)
distributions of characteristic atoms in Au3Cu-type ordered Au(1-x)Cux alloys corresponding to potential energy levels: (a) 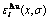 , σ=σmax; (b)
, σ=σmax; (b) 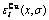 , σ=σmax; (c)
, σ=σmax; (c) 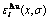 , σ=0.9σmax; (d)
, σ=0.9σmax; (d) 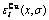 , σ=0.9σmax
, σ=0.9σmax
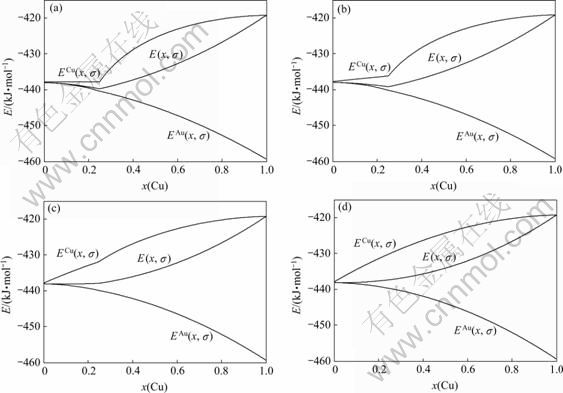
图6 Au3Cu型有序合金Au(1-x)Cux中合金和组元的摩尔势能 、
、 和
和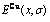 与成分和有序度的关系
与成分和有序度的关系
Fig.6 Molar potential energies  ,
, and
and 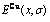 of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0.5σmax; (d) σ=0σmax
of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0.5σmax; (d) σ=0σmax
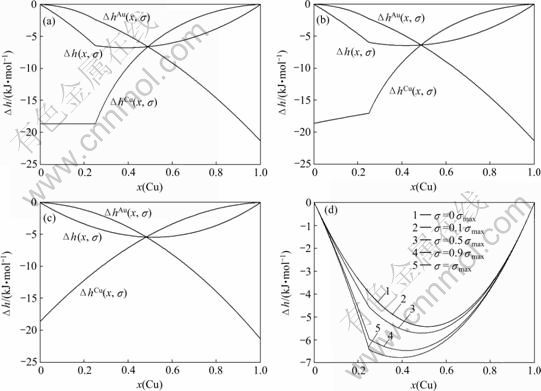
图7 0 K时Au3Cu型有序合金Au(1-x)Cux中合金和组元的平均生成焓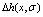 、
、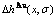 和
和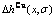 与成分和有序度的关系
与成分和有序度的关系
Fig.7 Molar formation enthalpies 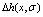 ,
,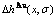 and
and 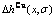 of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree at 0 K: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0σmax; (d)
of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree at 0 K: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0σmax; (d) 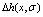 at different σ values
at different σ values
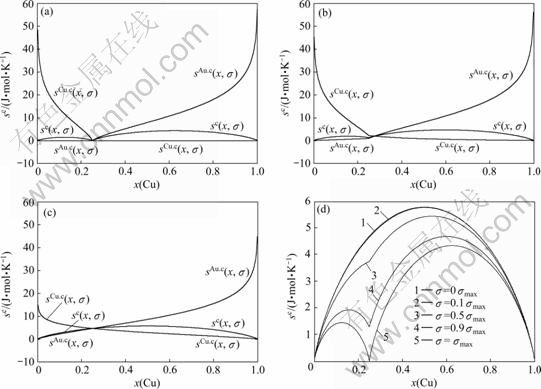
图8 Au3Cu型有序合金Au(1-x)Cux中合金和组元的组态熵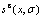 、
、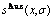 和
和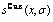 与成分和有序度的关系
与成分和有序度的关系
Fig.8 Configurational entropies 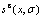 ,
,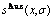 and
and 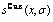 of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0σmax; (d)
of Au3Cu-type ordered Au(1-x)Cux alloys and their components as functions of composition and ordering degree: (a) σ=σmax; (b) σ=0.9σmax; (c) σ=0σmax; (d) 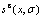 at different σ values
at different σ values
比较式(21)和式(25)可知,CAA模型和Bragg-Williams 模型的区别如下:CAA模型中,Au-Cu系的键能级别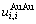 、
、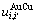 、
、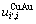 和
和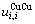 是恒定的,其对应的原子数分别为
是恒定的,其对应的原子数分别为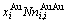 、
、 、
、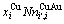 和
和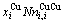 ;在 Bragg- Williams模型中,Au-Cu系的键能级别
;在 Bragg- Williams模型中,Au-Cu系的键能级别 、
、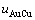 、
、 和
和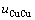 不是恒定的,其对应的原子数分别为
不是恒定的,其对应的原子数分别为
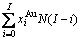 、
、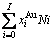 、
、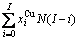 和
和 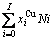 。
。
采用类似方法,可以确定特征原子团模型中合金相的摩尔势能与特征原子团势能的关系式。
根据以上分析,可得如下认识:
1) 在SSA框架中FCC基本格子Au-Cu系的基本结构单元是特征原子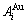 和
和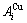 序列,基本能级是
序列,基本能级是 和
和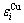 序列。它们可分别组成“组合结构单元序列”和“组合能级序列”。由13种
序列。它们可分别组成“组合结构单元序列”和“组合能级序列”。由13种 和13种
和13种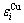 特征原子势能可组合成
特征原子势能可组合成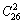 =325种特征原子对键能
=325种特征原子对键能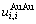 、
、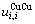 和
和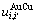 ,计算合金组态熵时应采用特征原子简并因数,即式(9)。
,计算合金组态熵时应采用特征原子简并因数,即式(9)。
因为合金相(即使为化合物)是组元原子按基本格子排列的溶体,所以,应该采用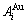 和
和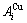 特征原子作为最小结构单元描述各种不同相结构:Au3Cu、AuCu、AuCu3化合物,Au3Cu、AuCu、AuCu3型有序合金和无序合金。同理,应采用特征原子的势能
特征原子作为最小结构单元描述各种不同相结构:Au3Cu、AuCu、AuCu3化合物,Au3Cu、AuCu、AuCu3型有序合金和无序合金。同理,应采用特征原子的势能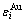 和
和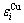 作为描述这些合金系统的最精细能级。
作为描述这些合金系统的最精细能级。
2) 不难认识当今流行的CALPHAD-CVM和FP-CVM理论的不足之处:由于采用“组合结构单元”,组态熵值往往估算过大;由于采用组合能级使得这些理论均为总能框架,组元的平均能量性质只能间接地由偏摩尔性质理论获得,然而,已经证明这是不正确的[1]。SSA则是能量可分离的框架。
5 结论
Au3Cu型有序合金特征原子势能配分函数的创新体现在如下3个方面:1) 以基本原子团 和
和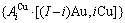 序列的中心特征原子
序列的中心特征原子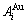 和
和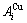 为结构单元序列,替代原子对和原子团,建立能阐明合金多样性的特征原子排列模型。2) 以配位原子组态
为结构单元序列,替代原子对和原子团,建立能阐明合金多样性的特征原子排列模型。2) 以配位原子组态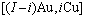 决定中心特征原子势能的方式替代原子对能量相互作用方式和原子团之间能量相互作用方式,以特征原子势能的基本能级替代“组元原子对”和“组元原子团”的能级,提出了以成分和有序度为变量的“特征原子势能相加定律”,计算合金相及其组元的平均势能。3) 在保持特征原子浓度与特征原子势能能级对应的条件下建立配分函数和计算组态熵。CAPE配分函数的重要意义在于它有可能推动材料科学由CALPHAD-CVM和FP-CVM总能量框架向能量可分离的EX-SSA和FP-SSA框架发展,使SSA框架具有坚实的哲学和物理学的基础。
决定中心特征原子势能的方式替代原子对能量相互作用方式和原子团之间能量相互作用方式,以特征原子势能的基本能级替代“组元原子对”和“组元原子团”的能级,提出了以成分和有序度为变量的“特征原子势能相加定律”,计算合金相及其组元的平均势能。3) 在保持特征原子浓度与特征原子势能能级对应的条件下建立配分函数和计算组态熵。CAPE配分函数的重要意义在于它有可能推动材料科学由CALPHAD-CVM和FP-CVM总能量框架向能量可分离的EX-SSA和FP-SSA框架发展,使SSA框架具有坚实的哲学和物理学的基础。
REFERENCES
[1] XIE You-qing. Systematic science of alloy[M]. Changsha: Central South University Press, 2010: 29-48, 405-427, 335-345.
[2] SUNDMAN B, FRIES S G, OATES A W. A thermodynamic assessment of the Au-Cu system[J]. CALPHAD, 1998, 22: 335-354.
[3] KIKUCHI R. A theory of cooperative phenomena[J]. Phys Rev, 1951, 81: 988-1003.
[4] SUNDMAN B, FRIES S G, OATES A W. A CALPHAD assessment of the Au-Cu system using the cluster variation method[J]. Z Metalkd, 1999, 90(4): 267-273.
[5] SATA M, de FONTAINE D, van SCHILFAARDE M. First-principles study of phase stability of Ti-Al intermetallic compounds[J]. J Mater Res, 1993, 8(10): 2554-2568.
[6] OATES W A. Configurational entropies of mixing in solid alloys[J]. Journal of Phase Equilibria and Diffusion, 2007, 28(1): 79-89.
[7] XIE You-qing, PENG Kun, LIU Xin-bi. Influences of xTi/xAl on atomic states, lattice constants and potential energy planes of ordered FCC TiAl-type alloys[J]. Physica B, 2004, 344: 5-20.
[8] XIE You-qing, LIU Xin-bi, PENG Kun, PENG Hong-jian. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl3-type alloys[J]. Physica B, 2004, 353: 15-33.
[9] XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti3Al-type alloys[J]. Physica B, 2005, 362: 1-17.
[10] XIE You-qing, TAO Hui-jing, PENG Hong-jian, LI Xiao-bo, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl2 type alloys[J]. Physica B, 2005, 366: 17-37.
[11] XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys[J]. Science in China: E, 1998, 41: 146-156.
[12] OZOLIN? V, WOLVERTON C, ZUNGER A. Cu-Au, Ag-Au, Cu-Ag and Ni-Au intermetallics: First-principles study of temperature-composition phase diagrams and structure[J]. Phys Rev B, 1998, 57: 6427-6442.
[13] HULTGREN R, DESAI P D, HAWKINS D T, GLEISER M, KELLEY K K. Selected values of thermodynamic properties of binary metals and alloys[M]. OH: American Society for Metals, 1963: 462.
[14] KITTEL C. Solid state physics[M]. 5th ed. New York: Wiley, 1976: 74.
[15] BRAGG W H, WILLIAMS E J. The effect of thermal agitation on atomic arrangement in alloys[J]. Proc Roy Soc A, 1934, 145: 699-730.
[16] LUPIS CHP. Chemical thermodynamics of materials[M]. Amsterdam: North-Holland, 1983: 452-469.
(编辑 陈卫萍)
基金项目:国家自然科学基金资助项目(51071181);湖南省自然科学基金资助项目(2010FJ4034)
收稿日期:2011-05-25;修订日期:2011-07-15
通信作者:谢佑卿,教授;电话:0731-88879287;E-mail: xieyouq2000@yahoo.com.cn
谢佑卿教授简介
谢佑卿,1937年出生,1962年毕业于中南矿冶学院金属物理专业,1961—1964年在吉林大学金属物理专业进修,1988—1989年在英国曼彻斯特理工大学作访问学者。现任中南大学国家材料物理与化学专业博士生导师,粉末冶金国家重点实验室教授。曾任第七届湖南省政协副主席,第九届、第十届湖南省人大常委会副主任,第九届、第十届全国人大常委会委员。致力于建立系统金属材料科学,创建了由“系统合金科学理论框架”和“特征原子排列设计工程”组成的“系统金属材料科学与工程”。完成了多项国家自然科学基金项目和湖南省重点科技项目,在国内外发表论文140余篇,出版专著《金属材料系统科学》和《Systematic Science of Alloys》2部,获国家科学大会奖和湖南省科技进步一等奖等多项奖励。