DOI： 10.11817/j.issn.1672-7207.2020.06.011
基于能耗效率的SiCp/Al复合材料切削参数多目标优化
王进峰,潘丽娟,邢迪雄,丁海民
（华北电力大学 能源动力与机械工程学院，河北 保定，071003）
摘要:为了提高加工质量，降低切削过程中的能源消耗，开展SiCp/Al复合材料切削加工参数的多目标优化研究。首先，确立以刀尖圆弧半径、切削深度、进给量、切削速度和刀具主偏角为输入参数，以最小表面粗糙度和最大功率系数为优化目标的优化方案。然后，通过仪器采集表面粗糙度、切削力和功率的实验数据，基于加权灰色关联和最小二乘拟合方法进行多目标优化，建立多目标预测模型。最后，利用主效应分析法来确定加工参数对功率系数、表面粗糙度和多目标模型的影响。研究结果表明：多目标预测模型能够获得最优参数组合，优化后可显著提高加工质量和功率系数。
关键词:功率系数；表面粗糙度；多目标参数优化；复合材料
中图分类号:TH14；TH17 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207（2020）06-1565-10
Multi-objective optimization of cutting parameters on turning SiCp/Al composites based on energy efficiency
WANG Jinfeng, PAN Lijuan, XING Dixiong, DING Haimin
(School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, China)
Abstract: To improve the machining quality and decrease the energy consumption for material cutting, cutting experiments of SiCp/Al composites were carried out to optimize the cutting parameters, Firstly, an optimization scheme was established, in which the nose radius, depth of cut, feed rate, cutting speed and the approach angle were the processing parameters, and the minimal surface roughness and the maximal power coefficient were the optimization objectives. Secondly, the experimental data of surface roughness, cutting force and power were collected by the experimental instruments. Based on the weighted grey relation and the least squares fitting method, the multi-objective prediction model was established. Finally, the impacts of processing parameters on power coefficient, surface roughness and multi-objective model wre determined using the main effect analysis approach. The results show that the model can obtain the optimal parameter combination, and can significantly improve the processing quality and power coefficient after optimization.
Key words: power coefficient; surface roughness; multi-objective parameters optimization; composite material
随着能源消耗和碳排放的增加，制造业对环境的影响越来越大。制造业消耗的能源占世界总能源的30%，排放的二氧化碳占全球总排放量的36%[1]，因此，节能减排已经成为制造业的首要任务。近年来，研究人员已经开始关注机械加工过程对生态的影响。BHATTACHARYA等[2]利用田口法研究了切削参数对功耗和加工质量的影响。CAMPOSECO-NEGRETE[3]利用方差分析法分析了切削参数对功率的影响。QASIM等[4]在对AISI1045进行加工时，采用了田口法和方差分析法来降低功耗和切削力等。CAMPOSECO-NEGRETE [5]应用方差分析和期望分析来优化车削铝时的能耗、材料去除率和表面粗糙度。BILGA等[6]使用田口方法研究了切削参数和刀尖圆弧半径对能耗的影响。NEWMAN等[7]研究表明通过优化切削参数和刀具路径，可节省6%~40%的能耗。由于切削参数对加工能耗的影响机理非常复杂，人们重点研究了功率消耗的参数化模型，为多目标参数优化问题提供了解决方案。GAITONDE等[8]建立了基于最小二乘拟合的数学模型，分析了加工时间和切削深度对功率、比切削力、刀具磨损和表面粗糙度的影响。ABHANG等[9]在不同的切削条件下建立了功率预测模型。MATIVENGA等[10]开发了最小能量预测模型，以确定最佳切削参数。VELCHEV等[11]提出了车削过程能耗的数学模型，分析了刀具材料、进给速度和切削深度对最小能耗的影响。LIU等[12]建立了槽铣削过程中刀具尖端切削力和切削功率的能耗模型，并进行了实验验证。LI等[13]提出了基于能效和生产时间的多目标优化模型。虽然大多数研究者在实验和模型中都考虑了机器的功耗，却忽略了功率系数这个重要参数。功率系数为切削材料消耗的功率与实际测量功率的比值。如果功率系数较低，电力局或供应商会对制造单位进行处罚。大部分对功率系数的研究主要集中于安装在机床上的矫正设备[14-15]，但这会增大研究成本。为了避免额外的资金投入，人们通过优化加工参数来提高功率系数。SHOKOOHI等[16]在研究一种新开发的切削液时测量了功率系数，但没有研究车削参数对功率系数的影响。BILGA等[6]对EN353合金钢进行了粗车削实验，获得了能源效率、机器消耗有功功率和功率系数这3个重要能耗响应参数的最佳切削条件。然而，这些研究所涉及的都是传统材料，对在航空航天和汽车等领域应用越来越广泛的SiCp/Al复合材料的研究较少。由于增强颗粒的存在，导致该材料切削加工性差，在加工过程中存在耗能高、加工质量差等问题[17-18]。王进峰等[19-20]针对高体积分数SiCp/Al复合材料切削时表面质量较差的问题，以表面粗糙度为优化目标，开展了不同切削用量和刀具形状的切削实验，得到不同参数组合条件下最小的表面粗糙度。然而，这些关于SiCp/Al复合材料的研究并没有涉及功率损耗的问题。针对SiCp/Al复合材料切削时所面临的问题，本文作者提出一种基于加工质量和可持续性的多目标优化方法。表面粗糙度是目前广泛用于评价产品质量的指标，能源消耗是可持续性的重要因素之一，因此，选定切削过程中的功率系数和表面粗糙度作为衡量可持续性和加工质量的指标，以最小表面粗糙度和最大功率系数作为目标，利用多响应权重因子的灰色关联法，对切削参数进行优化。
1 实验设计
1.1 流程设计
实验设计及参数优化的流程如图1所示。根据现有的研究结果，对实验参数和设备进行选择，通过调整实验数据的处理方式，建立符合拟合精度要求的多目标优化模型。
图1 多目标优化流程图
Fig. 1 Flowchart of multi-objective optimization
1.2 切削参数的选择
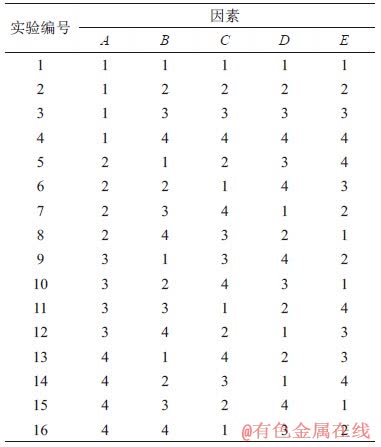
根据文献[19-20]，切削用量和刀具形状都会影响加工质量和加工效率，进而影响加工能耗，因此，本文以刀尖圆弧半径(因素A，mm)、切削深度(因素B，mm)、进给量(因素C，mm/r)、切削速度(因素D，m/min)和刀具主偏角(因素E，(°))作为优化参数，并使用田口法设计一组正交实验方案，该方法能够以最少的实验次数快速寻找到最佳的切削参数组合。实验因素及水平如表1所示，正交试验如表2所示。
1.3 实验设备和材料
切削实验所用的设备为数控机床LG Mazak CNC、聚晶金刚石刀片(PCD)和2020K11的刀杆，实验材料为SiC颗粒体积分数为45%的SiCp/Al复合材料。
表1 因素及水平
Table 1 Factors and levels
表2 正交试验设计
Table 2 Orthogonal array design
1.4 数据收集及处理
在机械加工过程中，功率消耗主要源于机床的待机功率、空转功率和切削材料所消耗的功率[21-22]。切削材料的功率可考虑由主运动功率和进给运动功率组成[23]。
(1)
(2)
式中：
为功率系数；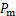
为切削材料消耗的功率；
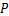为实际测量功率；
为主切削力；
为进给力；
为切削速度；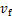
为进给运动速度。而对于车削运动而言，进给运动功率相对主运动功率很小，因此，本文忽略进给运动的功率消耗。
利用TR200粗糙度仪测量表面粗糙度，Kistler9272测力仪测量切削力，福禄克1 736功率分析仪测量每组实验所消耗的总功率。为了保证实验数据的准确性，每组实验参数下的表面粗糙度和功率测量3次，取平均值，得到的实验结果如表3所示。利用式(1)和式(2)计算出不同实验条件下的功率系数，如表4所示。
表3 实验数据
Table 3 Experimental data
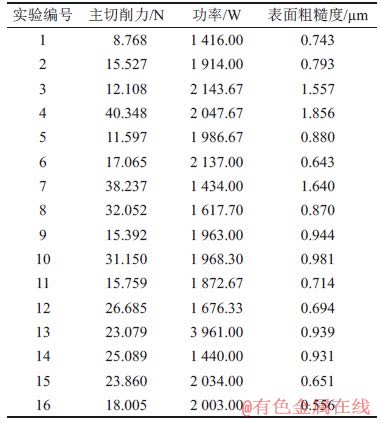
表4 不同实验条件下的功率系数
Table 4 Power factor at different experiment conditions
2 建立多目标优化数学模型
2.1 灰色关联分析
灰色系统理论是一种通过从现有数据中生成、挖掘和提取有用信息来研究具有部分已知信息不确定系统的方法。考虑总体的优化效果，本文使用灰色关联分析(grey relational analysis，GRA)将多响应优化模型转换成单一响应的灰色关联等级。
由于表面粗糙度和功率系数的单位不统一，首先需要实现2个优化目标的量纲一化。本文采用区间化数据处理方式对原始数据进行量纲一化处理。表面粗糙度的区间化数据处理是基于望小目标，使用式(3)进行量纲一化。功率系数区间化数据处理是基于望大目标，使用式(4)进行量纲一化。
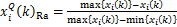(3)
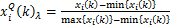(4)
然后，根据式(5)和(6)计算各偏移序列和灰色关联系数。
(5)
(6)
式中：i=1，2，
，n，n为实验次数，本文取n=16；k为因变量的数量，k=1，2，，m，m为因变量的个数，本文取m=2；
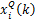为比较序列；
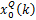为参考序列，
；
为偏移序列；
为灰色关联系数；
；
；
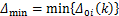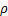为区分系数，取值范围为
，通常取值为0.5。
对于第1组实验来说，表面粗糙度和功率系数的关联度计算过程如下：
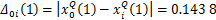(7)
(8)
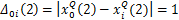
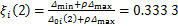(9)
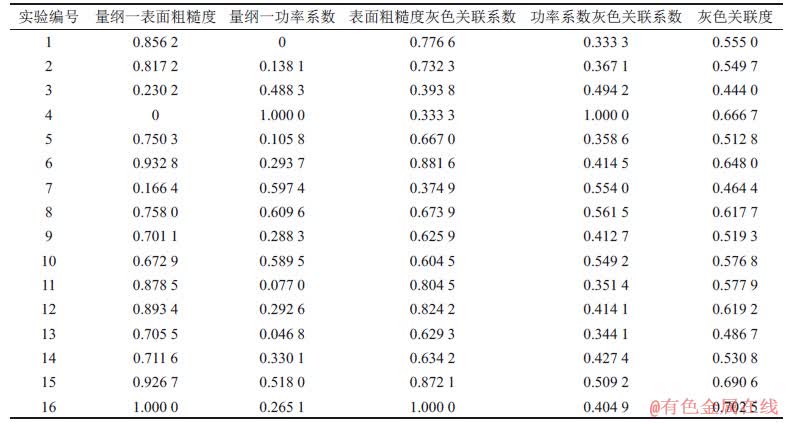
取2个优化目标权重相同，各占50%，则灰色关联度(FGRG)为0.555 0。不同实验条件下灰色关联度计算结果如表5所示。根据灰色关联法的意义，灰色关联度越大，说明该组获得的优化目标值越好。根据表5可知：第3组实验灰色关联度最小，表明该组表面粗糙度和功率系数的综合优化性能较差；而根据表3和表4可知，该组表面粗糙度为1.557 μm，在16组数据排第14位，功率系数为5.608%，在16组数据中排第6位。第16组实验数据灰色关联度最大，表明此时表面粗糙度和功率系数的综合优化性能较好；根据表3和表4可知，该组表面粗糙度为0.556 μm，在16组数据排第1位，但其功率系数为3.755%，在16组数据中排第11位，这表明第16组实验并不能作为优化的结果，需要进一步预测其他实验组合的结果。
表5 不同实验条件下灰色关联度计算结果
Table 5 Calculation results of gray relational grade at different experimental conditions
2.2 最佳切削参数组合的预测
鉴于上述分析并没有找到期望的优化结果，下面进一步利用田口法和建立多目标优化模型的方法对最优切削参数进行预测。
利用田口法对各因素各水平下的灰色关联度均值进行分析，分析结果见表6。从表6可知：刀尖圆弧半径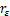
(因素A)在水平4(0.8 mm)时的灰色关联度最大，为0.602 6；切削深度
(因素B)在水平4(0.25 mm)时的灰色关联度最大，为0.651 5；进给量f(因素C)在水平1(0.02 mm/r)时的灰色关联度最大，为0.620 9；切削速度(因素D)在水平4(300 m/min)时的灰色关联度最大，为0.631 1，刀具主偏角
(因素E)在水平1(62.5°)时的灰色关联度最大，为0.610 0。可见：在A4B4C1D4E1的切削条件下，理论上能够取得最大的灰色关联度，也就是说，能够使表面粗糙度和功率系数的综合性能最好。
表6 灰色关联度在各因素各水平的均值
Table 6 Mean values of gray relational grade at all levels of each factor
为了准确地预测最优的切削参数，找到1个全局最优解，需要进一步建立灰色关联度与输入变量之间的关系。采用偏最小二乘法建立回归模型。基于表2和表5的数据，建立灰色关联度
的数学模型，如式(10)所示。
；
；
；
；
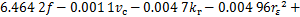
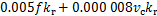
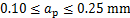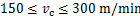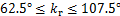。(10)
表7 灰色关联度的预测值与拟合值及其相对误差
Table 7 Predicted and fitted values of gray relational grade and relative error
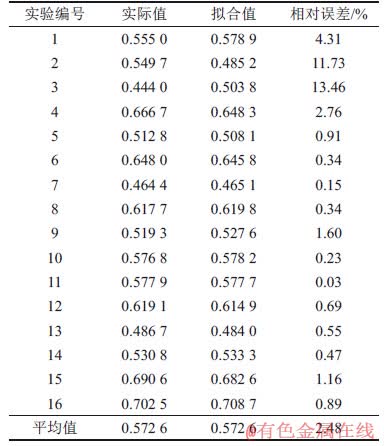
表8 预测模型的方差分析结果
Table 8 ANOVA results for the prediction model
为了验证式(10)在切削参数优化时的准确性，将16组正交实验数据代入式(10)，并计算相对误差，计算结果如表7所示。由表7可见：灰色关联度的预测值与实际计算值的平均相对误差在5%以内，这表明该模型能够较好地预测切削参数与灰色关联度系数之间的关系。为了进一步验证预测模型的准确性，对该模型进行方差分析，结果如表8所示，其中，R2为模型的相关系数，R2越大表示数据的相关性越强，模型的准确度越高。由表8可见：该模型的R2为0.946，说明模型具有较高的准确性。该模型所得结果与实验结果具有良好的相容性。因此，基于田口方法和灰色关联分析的多响应优化回归模型可作为预测模型。
3 结果与分析
3.1 主效应图分析
利用主效应分析法来确定各因素对功率系数、表面粗糙度和多目标函数的显著性影响，结果分别如图2~4所示。
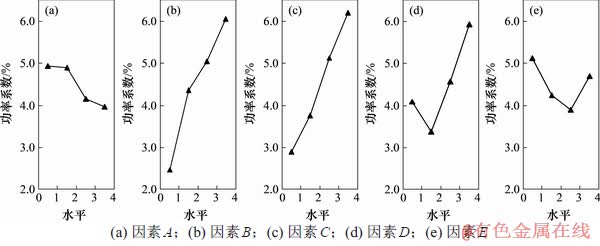
图2 切削参数对功率系数的主效应分析图
Fig. 2 Main effect plot of cutting parameters to power factor
由图2可以看出：切削深度和进给量对功率系数的影响最大，其次是切削速度和刀具主偏角，刀尖圆弧半径对功率系数的影响不显著。切削深度和进给量的增加会使切削过程中消耗的功率增加，即有功功率在总功率中所占的比例增大，功率系数变大。切削速度增大时会使切削力减小，根据上文切削材料所消耗功率的计算方法可知，当切削速度增大幅值小于切削力减小幅值时，切削功率会下降，功率系数减小；当切削速度增大幅值大于切削力的减小幅值时，切削功率上升，功率系数增大，因此，切削速度对功率系数的影响曲线会出现拐点。刀具主偏角会影响切削分力的比例关系，增大刀具主偏角，会使主切削力减小，进给力增大。由于在计算切削功率时忽略了进给功率，因此，在开始时，功率系数随着主偏角增大而减小，随着刀具主偏角的进一步增大，切削刃上的负荷随之增大，切削功率增大，因而功率系数变大。实验中所测量的切削力的变化印证了这一结论。
由图3可以看出：对表面粗糙度影响最大的是进给量，其次是刀尖圆弧半径和刀具主偏角，切削深度和切削速度对表面粗糙度的影响较小。在切削加工过程中，刀具相对于工件做进给运动，在被加工表面残留的面积越大，所得的表面将越粗糙，增大进给量和刀具主偏角、减小刀尖圆弧半径都会使残留的面积变大，从而降低加工质量。但在选择进给量和刀尖圆弧时应该注意，过小的进给量会使生产率呈比例减低，而且过小的进给量会造成薄层切削，激起振动。在高速切削过程中，当切削深度增加时，单位时间内材料去除体积变大，切削力也随之增加，对整个加工系统冲击作用变大，导致工件的表面质量变差；在小切削深度和大切削深度时，表面粗糙度出现了小范围的波动，这主要是切削系统机床的振动引起的。在一定范围内，随着切削速度的提高，表面粗糙度减小，但当切削深度增大到一定程度时，表面粗糙度有所上升。这是因为随着切削速度升高，产生的总切削热增大，但大部分被切屑带走，切削区表面温升不大，并不会使表面质量减低。但随着切削速度进一步升高，切屑与刀具的摩擦热增大，刀具前刀面和后刀面磨损加剧，而且较高的温度会降低碳化硅颗粒与铝基体的结合力，导致加工表面质量降低。
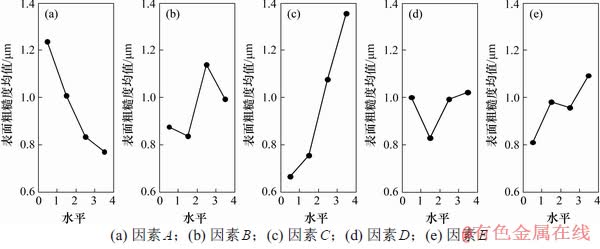
图3 切削参数对表面粗糙度的主效应分析图
Fig. 3 Main effect plot of cutting parameters to surface roughness
图4 切削参数对多目标函数的主效应分析图
Fig. 4 Main effect plot of cutting parameters to multi-objective function
由图4可以看出：切削深度对多目标函数(表面粗糙度和功率系数)的影响较大。进给量、切削速度、刀具主偏角和刀尖圆弧半径对多目标函数的影响程度依次减弱，刀尖圆弧半径的影响最小。
3.2 优化结果与实验验证
以min(-FGRG)为目标函数，利用MATLAB优化工具箱中的遗传算法(GA)对回归模型进行优化求解。求解的迭代过程如图5所示，得到的最优参数组合为：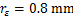
，
，
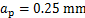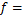
mm/r，
m/min，
，对应的FGRG最优解为0.907 937。由图5可知：迭代过程一直趋于收敛，在遗传到第90代后过程开始趋向平稳且最后稳定在固定值。
图5 遗传算法迭代过程图
Fig. 5 GA generations process diagram
为了验证优化结果的准确性，进行实验验证。将田口法优化和回归模型优化的结果与正交实验的最优组(16组)进行对比，如表9所示。由表9可以看出：与正交实验的最优参数组合相比，2种优化方法得到的功率系数和表面质量有显著提高，并且回归模型的优化结果更佳，说明这种回归方程较田口法更适合于切削参数优化。
表9 优化切削参数下的实验结果对比
Table 9 Comparison of experimental results at optimum cutting parameters
3.3 比较分析
由于研究内容和目标的差异性，本研究结果与现有文献的研究结果略有差异。BILGA等[24]利用田口法和方差分析法在车削加工过程中对功率系数及能源效率进行优化，但采用的材料是EN353合金钢，结果表明切削深度对功率系数的影响最显著，然后是进给量和进给速度，刀尖圆弧半径对功率系数的影响不大，本研究切削参数对功率系数的影响与之相同。然而，CAMPOSECO-NEGRETE[3]以AISI 6061 T6材料为研究对象，发现进给量是影响总功耗的最大因素，切削速度是影响最小的参数。KANT等[25]提出进给量是影响功耗和表面粗糙度最重要的因素，切削速度是最不重要的因素。这些差异的产生说明切削参数对功率系数与功率消耗的影响是不同的，文献[24]也证实了这一点。
SARIKAYA等[26]用最小二乘拟合建立了数学模型，发现灰色关联度实验值与预测值之间的平均相对误差为2.72%~7.14%。本文灰色关联度的实验数据与预测数据的平均相对误差为2.48%，与文献[26]中结果基本一致。
4 结论
1) 提出了基于最大功率系数和最小表面粗糙度的SiCp/Al复合材料切削参数多目标优化及预测模型。
2) 通过对模型的求解得到切削的最优参数组合如下：刀尖圆弧半径为0.8 mm，切削深度为0.25 mm，进给量为0.12 mm/r，进给速度为299.87 m/min，刀具主偏角为62.5°，并通过实验验证了这一结果。
3) 利用主效应分析法来确定加工参数对功率系数、表面粗糙度和多目标函数的影响，发现切削深度对多目标函数的影响较大，其次是进给量、切削速度和刀具主偏角，刀尖圆弧半径的影响最小。
参考文献：
[1] International Energy Agency. World energy outlook 2009 [EB/OL]. https: //www.iea.org/reports/world-energy-outlook-2009.
[2] BHATTACHARYA A, DAS S, MAJUMDER P, et al. Estimating the effect of cutting parameters on surface finish and power consumption during high speed machining of AISI 1045 steel using Taguchi design and ANOVA[J]. Production Engineering, 2009, 3(1): 31-40.
[3] CAMPOSECO-NEGRETE C. Optimization of cutting parameters for minimizing energy consumption in turning of AISI 6061 T6 using Taguchi methodology and ANOVA[J]. Journal of Cleaner Production, 2013, 53: 195-203.
[4] QASIM A, NISAR S, SHAH A, et al. Optimization of process parameters for machining of AISI-1045 steel using Taguchi design and ANOVA[J]. Simulation Modelling Practice and Theory, 2015, 59: 36-51.
[5] CAMPOSECO-NEGRETE C. Optimization of cutting parameters using response surface method for minimizing energy consumption and maximizing cutting quality in turning of AISI 6061 T6 aluminum[J]. Journal of Cleaner Production, 2015, 91: 109-117.
[6] BILGA P S, SINGH S, KUMAR R. Optimization of energy consumption response parameters for turning operation using Taguchi method[J]. Journal of Cleaner Production, 2016, 137: 1406-1417.
[7] NEWMAN S T, NASSEHI A, IMANI-ASRAI R, et al. Energy efficient process planning for CNC machining[J]. CIRP Journal of Manufacturing Science and Technology, 2012, 5(2): 127-136.
[8] GAITONDE V N, KARNIK S R, FIGUEIRA L, et al. Machinability investigations in hard turning of AISI D2 cold work tool steel with conventional and wiper ceramic inserts[J]. International Journal of Refractory Metals and Hard Materials, 2009, 27(4): 754-763.
[9] ABHANG L B, HAMEEDULLAH M, et al. Power prediction model for turning EN-31 steel using response surface methodology[J]. Journal of Engineering Science and Technology Review, 2010, 3(1): 116-122.
[10] MATIVENGA P T, RAJEMI M F. Calculation of optimum cutting parameters based on minimum energy footprint[J]. CIRP Annals, 2011, 60(1): 149-152.
[11] VELCHEV S, KOLEV I, IVANOV K, et al. Empirical models for specific energy consumption and optimization of cutting parameters for minimizing energy consumption during turning[J]. Journal of Cleaner Production, 2014, 80: 139-149.
[12] LIU N, ZHANG Y F, LU W F. A hybrid approach to energy consumption modelling based on cutting power: a milling case[J]. Journal of Cleaner Production, 2015, 104: 264-272.
[13] LI Congbo, LI Lingling, TANG Ying, et al. A comprehensive approach to parameters optimization of energy-aware CNC milling[J]. Journal of Intelligent Manufacturing, 2019, 30(1): 123-138.
[14] MAROUANI K, NOUNOU K, BENBOUZID M, et al. Power factor correction of an electrical drive system based on multiphase machines[C]//2014 First International Conference on Green Energy ICGE 2014. Sfax, Tunisia: IEEE, 2014.152-157.
[15] EL-MONIEM M S A, AZAZI H Z, MAHMOUD S A. A current sensorless power factor correction control for LED lamp driver[J]. Alexandria Engineering Journal, 2014, 53(1): 69-79.
[16] SHOKOOHI Y, KHOSROJERDI E, RASSOLIAN SHIADHI B. Machining and ecological effects of a new developed cutting fluid in combination with different cooling techniques on turning operation[J]. Journal of Cleaner Production, 2015, 94: 330-339.
[17] 丁志伟, 解丽静, 王涛, 等. 高体积分数SiCp/Al复合材料高速铣削力影响因素研究[J]. 新技术新工艺, 2013(2): 91-93.
DING Zhiwei, XIE Lijing, WANG Tao, et al. Research on high speed milling force on high fraction volume SiCp/Al matrix composites[J]. New Technology & New Process, 2013(2): 91-93.
[18] 于晓琳, 黄树涛, 赵文珍, 等. 高速铣削高体积分数SiCp/Al复合材料表面形貌及切屑机制的研究[J]. 中国机械工程, 2010, 21(5): 519-524.
YU Xiaolin, HUANG Shutao, ZHAO Wenzhen, et al. Study on surface morphology and chip formation by high-speed milling of high volume fraction SiCp/Al composites[J]. China Mechanical Engineering, 2010, 21(5): 519-524.
[19] 王进峰, 赵久兰, 储开宇. SiCp/Al复合材料切削力的仿真研究[J]. 系统仿真学报, 2018, 30(4): 1566-1571.
WANG Jinfeng, ZHAO Jiulan, CHU Kaiyu. Simulation study on cutting force of SiCp/Al composite[J]. Journal of System Simulation, 2018, 30(4): 1566-1571.
[20] 王进峰, 范孝良, 曹雨薇, 等. 高速车削SiCp增强铝基复合材料表面粗糙度试验[J]. 中国工程机械学报, 2017, 15(1): 62-66.
WANG Jinfeng, FAN Xiaoliang, CAO Yuwei, et al. Experimental investigations of surface roughness in high-speed turning of SiCp/Al composites[J]. Chinese Journal of Construction Machinery, 2017, 15(1): 62-66.
[21] 尹瑞雪. 基于碳排放评估的低碳制造工艺规划决策模型及应用研究[D]. 重庆: 重庆大学机械工程学院, 2014. 32-33.
YIN Ruixue. The study and application of process planning decision model for low carbon manufacturing based on carbon emissions evaluation[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2014. 32-33.
[22] DENG Zhaohui, ZHANG Hua, FU Yahui, et al. Optimization of process parameters for minimum energy consumption based on cutting specific energy consumption[J]. Journal of Cleaner Production, 2017, 166: 1407-1414.
[23] 喻怀仁. 金属切削原理[M]. 宁夏: 宁夏人民出版社, 1990. 77-78.
YU Huairen. Theory of metal cutting[M].Ningxia: Ningxia People's Publishing House, 1998. 77-78.
[24] BILGA P S, SINGH S, KUMAR R. Optimization of energy consumption response parameters for turning operation using Taguchi method[J]. Journal of Cleaner Production, 2016, 137: 1406-1417.
[25] KANT G, SANGWAN K S. Prediction and optimization of machining parameters for minimizing power consumption and surface roughness in machining[J]. Journal of Cleaner Production, 2014, 83: 151-164.
[26] SARIKAYA M, GULLU A. Taguchi design and response surface methodology based analysis of machining parameters in CNC turning under MQL[J]. Journal of Cleaner Production, 2014, 65: 604-616.
（编辑 伍锦花）
收稿日期： 2019 -11 -21; 修回日期： 2020 -01 -17
基金项目(Foundation item)：国家自然科学基金资助项目(51301068)；河北省自然科学基金资助项目(E2019502057，E2019502060)；河北省高等学校科学技术研究资助项目(Z2015127)；中央高校基本科研业务费专项资金资助项目(17MS148) (Project(51301068) supported by the National Natural Science Foundation of China; Projects(E2019502057，E2019502060) supported by the Natural Science Foundation of Hebei Province; Project(Z2015127) supported by the Science and Technology Research of Higher Education of Hebei Province; Project(17MS148) supported by the Foundation Research Funds for the Central Universities)
通信作者：王进峰，博士，副教授，从事数字化制造研究；E-mail: wjf266@163.com
