节理特征对TBM盘形滚刀破岩特性的影响

谭青^{1, 2}，朱逸¹，夏毅敏^{1, 2}，徐孜军¹，李建芳¹，宋军华³

(1. 中南大学 机电工程学院，湖南 长沙 410083；

2. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083；

3. 湘潭大学 机械工程学院，湖南 湘潭 411105)

摘要：为了研究节理特征对全断面岩石掘进机(TBM)盘形滚刀破岩机制的影响，从岩体细观尺度出发，基于颗粒离散元法建立不同节理强度、间距和倾角特征下盘形滚刀破碎中分化灰岩的数值模型，模拟TBM滚刀切削岩石时岩石裂纹生成、扩展和碎块形成的全过程，以及滚刀受力和岩石应力分布状态。研究结果表明：岩体中的节理面能改变裂纹扩展方式，阻隔损伤向节理面下的岩石传播，且低强度节理面阻隔损伤的能力较强；节理间距对岩碴的块状大小有较大影响，当节理间距减小时破岩效率升高；节理岩体存在3种基本的破碎模式，主要与节理倾角有关；当节理倾角为60°时，破岩比能耗最小，滚刀破岩效率达到最高值。

关键词：节理特征；盘形滚刀；破岩；颗粒离散元；数值模拟

中图分类号：TP391.9；U455.3⁺1          文献标志码：A         文章编号：1672-7207(2013)10-4040-07

Influence of joint characteristics on rock fragmentation induced by TBM disc cutter

TAN Qing^{1, 2}, ZHU Yi¹, XIA Yimin^{1, 2}, XU Zijun¹, Li Jianfang¹, SONG Junhua³

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;

3. School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

Abstract: In order to study the effects of joint characteristics on rock fragmentation modes, from the meso-level structure of rock mass, the jointed rock indentation by a single TBM disc cutter was simulated by using the particle discrete element method, and rock fragmentation process was highlighted. A series of two-dimensional numerical modeling in jointed rock mass were performed to explore the influence of joint strength, spacing and orientation on rock fragmentation by disc cutter. Finally the load of disc cutter and the stress distribution of rock were analyzed. The results show that the joints in the rock mass can change the crack propagation pattern and obstruct the damage spread into the rocks under the joints. For the low strength joint in the rock mass, the ability of obstructing damage spread is better. The joint spacing has significant impact on the size of rock debris and the penetration rate increases with the decrease of the joint spacing. There exists three basic modes of rock fragmentation which are mainly related to the joint orientation. The specific energy achieves the minimum value at the joint dip angle α=60° and the penetration efficiency of disc cutter can reach the highest.

Key words: joint characteristics; disc cutter; rock fragmentation; particle discrete element; numerical simulation

随着全断面岩石掘进机(tunnel boring machine，简称TBM)在隧道工程建设中广泛应用，实现TBM高效破岩成为掘进施工亟待解决的关键问题^[1]。而各种地质因素如节理、岩溶、高地应力等均会影响TBM破岩效率^[2-3]。目前，国内外众多学者采用理论分析、试验测试及数值模拟等手段对节理倾角和间距进行了研究，如：Howarth^[4]于20世纪80年代初通过试验研究了岩体节理的数量、开度和频度等对刀具切削的影响，发现对于给定的切深，推进力随着节理间距减小而减少；Bruland^[5]于1998年提出隧道掘进机NTNU模型，对节理倾角影响TBM破岩速率进行了定性分析；Barton等^[6]通过建立模型来预测不同地质条件下TBM掘进速率，并将节理倾角作为预测TBM掘进速率的因素之一；Kou等^[7-8]研究了非均质岩石的破碎过程，并将典型裂纹系统划分为径向裂纹、中间裂纹和侧向裂纹；Liu等^[9-10]采用R-T^2D软件建立了刀具压入岩石的有限元单元模型，模拟了岩石裂纹的生成与扩展过程；苏利军等^[11]采用颗粒流方法，对滚刀破岩过程的挤压-张拉破坏机制进行了模拟；Wu等^[12]将离散单元法应用于土压平衡盾构压力舱内沙土流动性问题，取得较好的效果；张魁等^[13-14]通过离散元方法中的UDEC程序建立了不同围压及切削顺序下滚刀侵入岩石的离散元模型，研究了岩石裂纹的扩展机制。鉴于隧道施工的特殊地质环境及破岩机制的复杂性，尤其是滚刀与节理岩体的相互作用过程尚未完全认识，本文在合理简化实际工况的基础上，从细观角度对TBM盘形滚刀破岩过程进行颗粒离散元模拟，并对结果进行统计分析，力图从细观机制着手来解释不同节理特征对TBM盘形滚刀破岩特性影响效应的问题，以便为数值模拟技术在刀具破岩研究中的应用提供参考。

1  TBM滚刀破岩的颗粒流模型

1.1  岩层参数

根据长沙市某地铁施工区间的岩土工程勘察报告，选取具有代表性的主要岩层即中风化灰岩，其节理裂隙极发育，岩石质量指标为10%~40%，岩质坚硬，属较软岩—较硬岩，岩体基本质量等级为Ⅳ类，具体力学参数见表1。

1.2  岩石材料宏细观力学参数的匹配

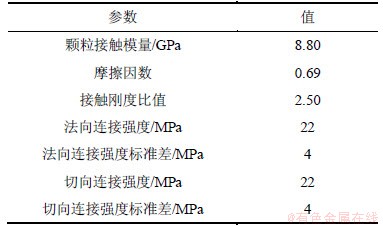
颗粒流模型的细观参数一般不能直接、简单地与材料一系列的宏观物理力学参数相联系，这与连续介质模型有着本质差别。对于岩石类材料，细观参数主要通过模拟单轴压缩和巴西圆盘试验进行反复选择和标定，直至与岩石的宏观力学性能相符为止。设定岩石试件数值模型的最大半径R_max和最小颗粒半径R_min之比为1.2，颗粒的最小半径取0.3 mm；考虑初始孔隙率为0.2时的颗粒密度ρ=2 740 kg/m³。单轴压缩试验试样长×宽为100 mm×50 mm，巴西圆盘试验试样的直径为50 mm，得到岩石材料的颗粒细观参数见表2。同时，为了能更加接近岩石材料的物理特性，选用平行粘结模型来模拟颗粒之间的接触方式。

表1  典型岩石力学参数

Table 1  Mechanical parameters of typical rock material

表2  岩石材料对应细观力学参数

Table 2  Meso-mechanical parameters for rock material

1.3  滚刀破岩模型

Innaurato等^[15]采用平面等效的方式，发现忽略扭矩产生的切向滚动力影响，将滚刀破岩过程近似简化为二维平面问题是基本可行的。为此，本文在前人研究基础上将滚刀破岩简化成二维平面问题，对滚刀作用下岩石裂纹的扩展及岩石应力分布情况进行近似模拟。

与岩石相比，滚刀刀圈的刚度和强度都非常高，因此，将其视为刚性体，将滚刀刀圈轮廓用刚性墙体表示。本文以应用最广泛的适应软到中硬岩地层的近似常截面盘形滚刀为研究对象，确定其主要几何参数：滚刀刀刃顶部宽度B=10 mm，过渡圆弧半径r=4 mm，刀刃角γ=20°。

建立1个长×宽为400 mm×160 mm岩石试件模型，如图1所示。岩体中节理面与滚刀贯入方向的夹角为α，节理面间距为s，观察不同节理面强度、间距和倾角下裂纹扩展现象及应力应变规律。

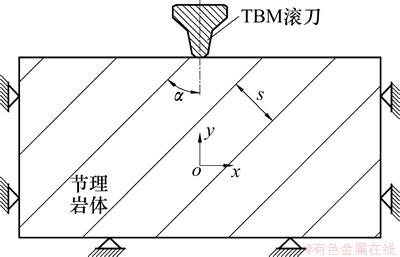
图1  盘形滚刀破岩颗粒流模型

Fig. 1  Numerical model of rock fragmentation by TBM disc cutter

2  节理特征对破岩过程的影响

自然界中岩体的节理分布往往比较复杂，而且盘形滚刀与节理的相对位置也不断发生变化，因此，需对实际问题进行必要简化。假定岩体中只存在一组规则布置的节理，通过改变节理面强度、倾角和间距来研究节理特征对TBM滚刀破岩过程的影响。

2.1  节理面强度

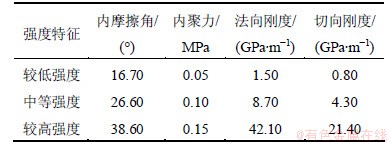
节理面强度主要指抗剪强度，当岩体节理面上切向应力大于抗剪强度时，节理面发生剪切错动或滑动，进而导致岩体破坏。因此，采用JSET命令来修改沿指定轨迹的接触特性，创建具有任意产状分布的节理面，其力学性质如表3所示。

表3  节理面力学性质

Table 3  Mechanical properties of joints

在中风化灰岩试件中设置间距为40 mm的节理面，节理面与滚刀贯入方向相垂直，贯入度为10 mm，通过颗粒离散元模拟，得到不同节理面强度下盘形滚刀破岩过程，如图2所示。

图2  节理面强度对破岩过程的影响

Fig. 2  Influences of different joint planes on rock fragmentation process

当节理面的强度较低时，滚刀压入岩体时表层与深层的节理面就立即发生损伤，在刀具正下方的节理面以颗粒间张拉破坏为主，而两侧以剪切破坏为主，表明破坏是节理面两侧相对错动造成的。随着滚刀贯入度的增大，表层岩石逐渐被破坏，损伤逐渐深入岩石内部，在达到第1个节理面后损伤的渗透能力将下降，但会导致第1个节理面的破坏程度大大提高，最终可能使第1节理面上的表层岩石全部发生破碎，形成含有节理面的大块状岩碴，而深部节理面由中间裂纹直接贯穿，如图2(a)所示。

当滚刀作用在具有中等强度节理面的岩体上时，表层与深层的节理面不会立即发生损伤。随着贯入度的增大，最表层节理面上逐渐发生损伤破坏，表层岩体形成挤压破碎区，并通过剪切破坏使深层岩体产生微裂纹，但不会导致深部节理面松动，如图2(b)所示。当节理面的强度很高时，节理面不会因滚刀的碾压而发生松动，同时其阻隔损伤进一步渗透的作用也随之消失，相当于节理面不存在的效果，进而裂纹贯穿到第3层节理，如图2(c)所示。

微裂纹数量随节理面强度变化直方图如图3所示。从图3可见：随着节理面强度的变化，产生的裂纹数有明显差异，节理面强度较低时产生的裂纹数量是中等强度的2倍多，其破碎面积相应增大；同时，当节理强度较低时，剪裂纹数目大于拉裂纹数目，这表明裂纹以颗粒间剪切破坏为主，宏观破坏是由节理面的相对错动造成的。随着节理强度的增加，节理面抵抗损伤的能力增强，裂纹数逐渐减少，破坏方式是张拉和剪切共同作用的。

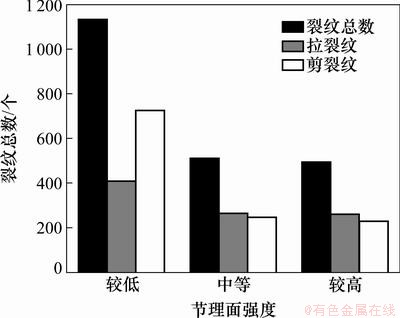
图3  微裂纹数量随节理面强度变化直方图

Fig. 3  Histogram of microcracks number with joint plane strength

2.2  节理间距与倾角

设定岩体中节理面之间的内摩擦角为26.6°，内聚力为0.1 MPa，节理面与滚刀贯入方向的夹角分别为0°，15°，30°，45°，60°，75°和90°，节理面间距分别取40，80和120 mm，分析节理间距及节理倾角对破岩过程的影响。

2.2.1  节理倾角对破岩过程的影响

当滚刀贯入岩石表面时，压碎区首先出现在完整岩石部分；随着滚刀贯入度逐渐增大，岩石中的破裂损伤将集中发生在节理面上，而节理面对裂纹扩展具有显著的控制性作用；随着节理倾角的变化，岩石的破坏过程也各有其不同之处，体现在：(1) 当节理倾角α=0°时，滚刀对岩石损伤程度不大，而当α＞0°时，节理面自始至终都对滚刀的破岩过程有显著影响；(2) 当节理倾角α较小时，节理面将引导裂纹向岩石深部扩展，当节理倾角α=30°时，滚刀对岩体有明显的劈裂作用，如图4(a)所示；当α较大时，节理面则会引导裂纹横向扩展，而裂纹的横向扩展更利于岩碴的形成，易形成大块岩碴。可见，不同节理倾角的岩体主要存在3种破碎模式：第1种是α较小，即节理面近似平行于贯入方向时，节理面将引导裂纹向岩石深部扩展，到一定贯入度时，破碎区的侧向裂纹与节理面或自由面交汇，进而形成碎块，如图4(a)所示；第2种是α较大(α≥60°)时，节理面受到刀具的剪切作用，致使裂纹从节理面起裂并向节理面或自由面扩展形成碎块，如图4(b)所示；第3种是当α接近90°时，从刀具作用下方的压碎区产生裂纹，并扩展到节理面或自由面形成碎块，如图4(c)所示。

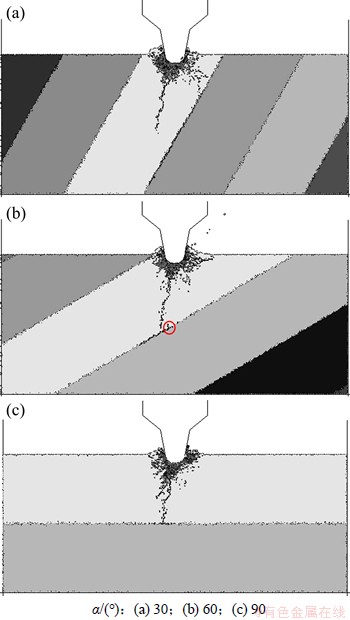
图4  节理间距s=80 mm时不同节理倾角的岩石破碎模式

Fig. 4  Rock fragmentation pattern at joint spacing s=80 mm

统计得到滚刀受力均值与标准差随节理倾角的关系如图5所示。由图5可知：当节理间距s=80 mm时，随着节理倾角的变化，水平力在零点上下有小范围波动，而垂直力普遍处于较大值，其标准差比水平力的大，表明波动较剧烈，符合岩石阶跃破碎的特点；同时，对于不同的节理倾角，滚刀受力无明显变化趋势，这表明节理倾角对滚刀受力影响较小。

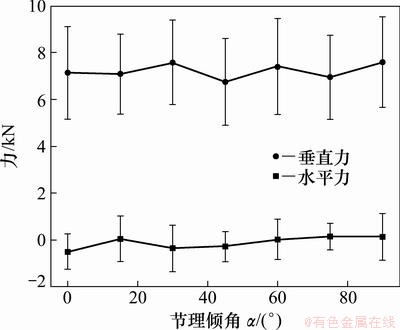
图5  切削力随节理倾角变化趋势

Fig. 5  Relationship between cutting force and joint orientation

2.2.2  节理间距对破岩过程的影响

经统计得到节理间距对微裂纹数量的影响如图6所示。从图6可以看到：随着节理间距的增大，微裂纹数逐渐减少，表明破碎岩碴量相应减小。

当节理间距s≤80 mm时，岩石的破裂以节理面的破坏为主，易形成含有节理面的大块岩碴；当节理间距s≥120 mm时，以岩层的自由面破坏为主。因此，当岩体中存在中等强度且密集分布的节理面时，有利于掘进效率提高。

对比不同节理间距可以发现TBM滚刀破岩过程可分为2个阶段：正常破岩和节理面破岩。当节理面间距较大时，滚刀下形成的裂纹不足以达到节理面，裂纹的扩展、贯通以形成岩片为主，如图7(a)所示；当节理间距较小时，滚刀作用于岩体，形成的裂纹能达到节理面，并与节理面贯通形成大块碴片，如图7(b)所示。在实际工程中，TBM处于连续掘进状态，这2种破岩状态交替进行，进而会出现薄岩片和大块岩碴交替出现的情况。

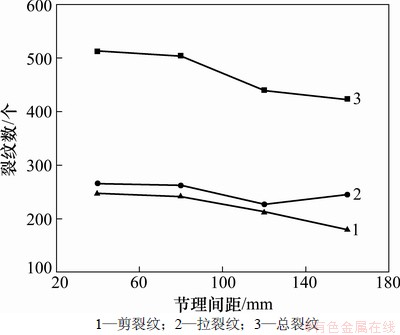
图6  微裂纹数量与节理间距的关系

Fig. 6  Relationship between microcracks number and joint spacing

2.3  岩石的垂向应力云图

将岩石试件的垂向应力输出并绘制成不同节理倾角的应力云图，如图8所示。

由图8可知：由于存在节理，垂向应力场的分布不再对称，而是随节理面发生偏转，且随着α的增大，其偏转程度变大。由沿节理面的应力分布可得出：当α增大到60°时，在作用力垂直于节理面的交点处开始出现拉应力，如图8(d)所示。这一规律较好地解释了第2种破岩模式中裂纹由节理面生成且垂直于节理面方向起裂的现象。

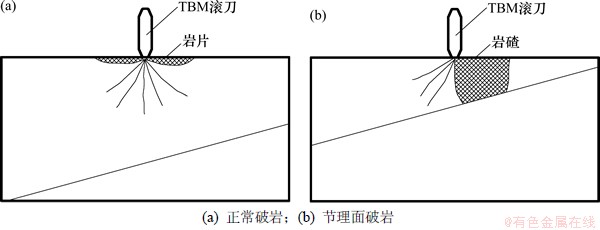
图7  节理间距对滚刀破岩的影响

Fig. 7  Effect of joint spacing on rock fragmentation pattern

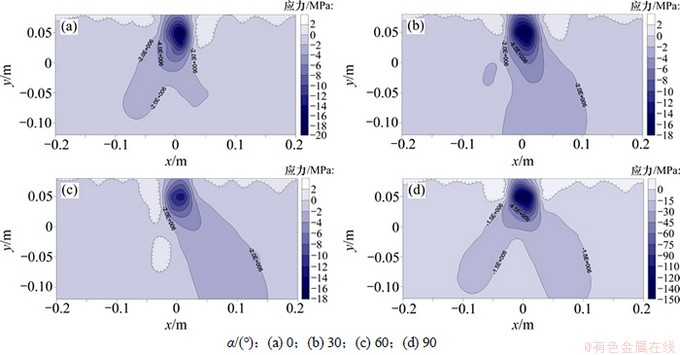
图8  节理间距s=120 mm，不同节理倾角的垂向应力云图

Fig. 8  Vertical stress contour map: joint spacing s=120 mm, five different joint orientations

3  节理特征对滚刀破岩效率的影响

节理间距和倾角对TBM盘形滚刀破岩效率的影响通过计算破岩比能耗S_E，即破碎单位面积滚刀所作的功得到。

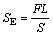                 (1)

其中：F为盘形滚刀所受的y向平均力；L为贯入深度；S为破碎面积。

破岩比能耗间接反映了TBM盘形滚刀的破岩效率。破岩所需破碎功越小、破碎面积越大，则破岩效率越高。不同节理间距和倾角的数值模拟结果如表4所示。

在计算破碎面积时，考虑了滚刀破碎中风化灰岩的最优刀间距为100 mm的情况^[16]，并根据裂纹扩展模式和不同节理特征计算破碎面积。

破岩比能耗与节理间距和倾角的关系如图9所示。由图9可见：破岩比能耗随着节理倾角α的增加有一个逐渐减少然后增大的过程；对于同一节理倾角，其破岩比能耗随着节理间距增大而不断增大；当中风化灰岩中节理倾角α=60°时，盘形滚刀的破碎效率达到最高值。

表4  不同节理间距及倾角的破岩试验结果

Table 4  Results of indentation test with different joint orientations and spacings

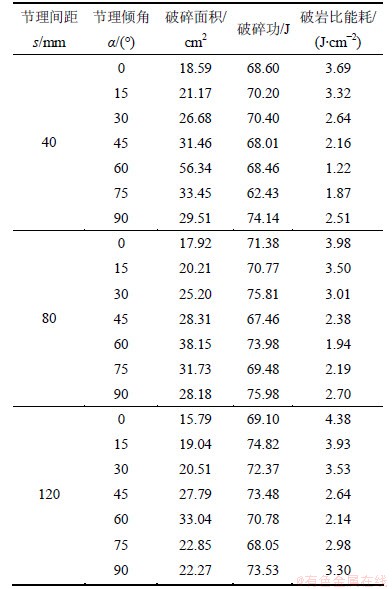
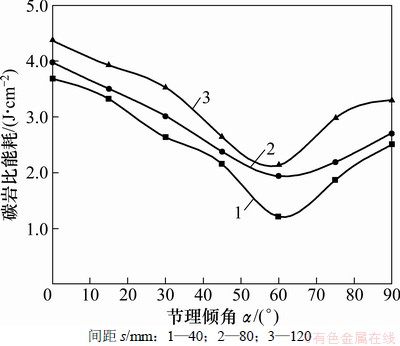
图9  节理间距和倾角对破岩效率的影响

Fig. 9  Effect of joint orientation and spacing on penetration efficiency

4  结论

(1) 在TBM盘形滚刀作用下，岩体中的节理面能显著影响裂纹生成及扩展方向，并阻隔损伤向节理面下的岩石渗透；低强度节理面阻隔损伤的能力较强。

(2) 当岩体节理间距s≤80 mm时，滚刀破岩时以节理面破坏为主，易形成含有节理面的大块岩碴；当节理间距s≥120 mm时，以岩体自由面上岩片破碎为主，且间距对岩碴的块状大小有较大影响。

(3) 在滚刀作用下节理岩体存在3种破碎模式：第1种是α较小时，节理面引导裂纹向岩石深部扩展，而破碎区的侧向裂纹与节理面或自由面交汇形成碎块；第2种是α较大(α≥60°)时，节理面受到刀具的剪切作用，致使裂纹从节理面起裂并向节理面或自由面扩展形成碎块；第3种是当α接近90°时，从刀具作用下方的压碎区产生裂纹，并扩展到节理面或自由面形成碎块。

(4) 从滚刀破岩效率来看，在中分化灰岩中存在一个最优节理倾角。当节理倾角为60°时，破岩比能耗最小，滚刀破岩效率达到最高值。

参考文献：

[1] Roby J, Sandell T, Kocab J, Lindbergh L. The current state of disc cutter design and development directions[C]//North American Tunneling 2008 Proceedings. San Francisco，USA, 2008: 36-45.

[2] Hassanpour J, Rostami J, Zhao J. A new hard rock TBM performance prediction model for project planning[J]. Tunnelling and Underground Space Technology, 2011, 26(5): 595-603.

[3] Farrokh E, Rostami J. Effect of adverse geological condition on TBM operation in Ghomroud tunnel conveyance project[J]. Tunnelling and Underground Space Technology, 2009, 24(4): 436-446.

[4] Howarth D F. The effect of jointed and fissured rock on the performance of tunnel boring machines[J]. Proceedings of the International Symposium on Weak Rock. Tokyo, 1981: 1069-1074.

[5] Bruland A. Hard rock tunnel boring[D]. Trondheim: Norwegian University of Science and Technology, 1998: 57-67.

[6] Barton N. TBM tunnelling in jointed and faulted rock[M]. Taylor & Francis, 2000: 30-37.

[7] Kou S Q, Huang Y, Tan X C, et al. Identification of the governing parameters related to rock indentation depth by using similarity analysis[J]. Engineering Geology, 1998, 49(3/4): 261-269.

[8] Kou S Q, Lindqvist P A, Tang C A, et al. Numerical simulation of the cutting of inhomogeneous rocks[J]. Rock Mechanics and Mining Sciences, 1999, 36(5): 711-717.

[9] Liu H Y, Kou S Q, Lindqvist P A, et al. Numerical simulation of the rock fragmentation process induced by indenters[J]. Rock Mechanics and Mining Sciences, 2002, 39(4): 491-505.

[10] Liu H Y, Kou S Q, Lindqvist P A, et al. Numerical modelling of the heterogeneous rock fracture process using various test techniques[J]. Rock Mechanics and Rock Engineering, 2007, 40(2): 107-144.

[11] 苏利军, 孙金山, 卢文波. 基于颗粒流模型的TBM滚刀破岩过程数值模拟研究[J]. 岩土力学, 2009, 30(9): 2823-2829.

SU Lijun, SUN Jinshan, LU Wenbo. Research on numerical simulation of rock fragmentation by TBM cutters using particle flow method[J]. Rock and Soil Mechanics, 2009, 30(9): 2823-2829.

[12] Wu L, Qu F Z. Discrete element simulation of mechanical characteristic of conditioned sands in earth pressure balance shield tunneling[J]. Journal of Central South University of Technology, 2009, 16(6): 1028-1033.

[13] 张魁, 夏毅敏, 谭青, 等. 不同围压条件下TBM刀具破岩模式的数值研究[J]. 岩土工程学报, 2010, 32(11): 1780-1787.

ZHANG Kui, XIA Yimin, TAN Qing, et al. Numerical study on modes of breaking rock by TBM cutter under different confining pressures[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1780-1787.

[14] 谭青, 徐孜军, 夏毅敏, 等. 两种切削顺序下TBM刀具破岩机理的数值研究[J]. 中南大学学报: 自然科学版, 2012, 43(3): 940-946.

TAN Qing, XU Zijun, XIA Yimin, et al. Numerical study on mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University: Science and Technology, 2012, 43(3): 940-946.

[15] Innaurato N, Oggeri C, Oreste P P, et al. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J]. Rock Mechanics and Rock Engineering， 2007, 40(5): 429-451.

[16] Moon T, Oh J. A study of optimal rock-cutting conditions for hard rock tbm using the discrete element method[J]. Rock Mechanics and Rock Engineering, 2012, 45(5): 837-849.

(编辑  陈灿华)

收稿日期：2012-10-12；修回日期：2012-12-23

基金项目：国家重点基础研究发展计划(“973”计划)项目(2013CB035401)；国家自然科学基金资助项目(51274252，51074180)；湖南省科技重大专项(2010FJ1002)；湖南省科技支撑计划项目(2010GK3073)

通信作者：谭青(1955-)，男，湖南长沙人，博士，教授，从事岩石切削机理的研究；电话：13974870965；E-mail：tanqing@csu.edu.cn