脉冲GTAW熔池行为和焊缝成形的三维数值模拟
高如超,饶政华,李芸霄,廖胜明
(中南大学 能源科学与工程学院,湖南 长沙,410083)
摘要:建立脉冲电流下钨极气体保护电弧焊(GTAW)的三维非稳态数值模型,研究焊接过程中的熔池输运现象及其对焊缝成形的影响。模拟不同条件下熔池内瞬态温度和速度分布、熔池形态变化以及焊缝形状。研究研究表明:电流方式对GTAW焊接的熔池行为和焊缝形状有重要的影响;在脉冲电流下,电流强度的波动造成熔池周期性的振荡和凝固速率的变化,从而在焊缝表面产生焊波;在连续电流下,熔池的形态变化和凝固是连续的过程,不会产生焊波;脉冲电流频率增加,导致沿焊接方向上的凝固速率减小,焊波的间距和高度减小。
关键词:GTAW;脉冲电流;熔池;焊缝;数值模拟
中图分类号:TG44 文献标志码:A 文章编号:1672-7207(2013)11-4712-08
Three-dimensional modeling of weld pool dynamics and weld bead formation during pulsed GTAW
GAO Ruchao, RAO Zhenghua, LI Yunxiao, LIAO Shengming
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The complex transport phenomena and their effect on weld pool dynamics and the formation of weld bead in moving gas tungsten arc welding (GTAW) under the pulsed current were studied by using a 3D transient numerical model. The transient distributions of the temperature and melt flow velocity in the weld pool, weld pool dynamics, and solidified weld bead were simulated. The results show that the current pattern has significant effects on the weld pool dynamics and weld bead shape in GTAW. The surface ripples are formed under pulsed current by the interplay between the up-and-down weld pool dynamics, caused mainly by the periodically varied current and the weld pool solidification rate. Under continuous current, weld ripple is not observed due to the continuous weld pool dynamics and solidification. The larger pulsed current frequency tends to decrease the solidification rate and thus the pitch and height of the ripples are reduced.
Key words: gas tungsten arc welding; pulsed current; weld pool; weld bead; numerical simulation
脉冲GTAW焊接的电流幅值按照一定频率周期性地变化,交替出现峰值电流和基值电流。在每个脉冲中,峰值电流加热和熔化工件形成熔池,基值电流维持电弧燃烧同时使输入工件的热量减少,因此,脉冲GTAW过程具有较好的电弧特性和较低的热量输入,其应用日益广泛[1]。熔池凝固后在工件上形成相互搭接而成的焊缝[1-2]。焊缝的最终形状是评判整体焊接性能的重要指标,它对焊接件的结构应力、焊接接头的强度和疲劳寿命等有重要的影响。脉冲GTAW焊缝表面还伴随着焊波的产生[1-2],它与焊接过程中偏析、多孔等微结构缺陷有关。许多研究者利用实验[3-6]和数值[7-9]方法研究GTAW焊接的熔池行为和焊缝成形。由于高温电弧以及母材金属的不透明性,许多参数(如温度、速度等)难以用实验方法测得,无法获得对脉冲GTAW过程的完全理解。Kim等[7]研究了脉冲GTAW焊接熔池内的流动、传热和相变的现象。武传松等[8]分析了脉冲电流对GTAW焊接熔池流场、温度场和形状的影响。赵明等[9]建立三维GTAW模型研究了移动热源作用下不锈钢薄板熔池行为。然而,焊接电流对脉冲GTAW焊缝成形以及表面焊波的影响尚未获得足够的重视,为此,本文作者应用流体容积法(VOF)和连续介质模型建立三维非稳态的GTAW移动焊模型,模拟不同电流方式下的熔池行为和焊缝形成过程。
1 数学模型
1.1 控制方程
图1所示为GTAW平板堆焊过程的示意图。三维x–y–z坐标系统设在固定的金属平板上;二维r–z轴坐标系统设在电弧中心,并随之移动。假定电弧随电极沿x轴正方向匀速移动。本模型不包含电弧生成的过程,并假定电弧热和电弧压力在工件表面呈高斯分布[10]。该模型建立的非稳态控制方程组如下。
连续性方程:
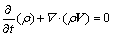 (1)
(1)
动量方程:

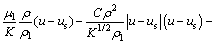
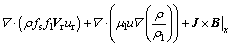 (2)
(2)
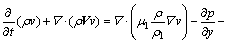
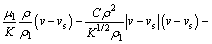
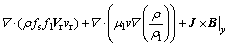 (3)
(3)
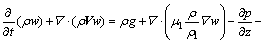
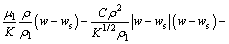
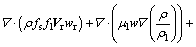
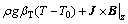 (4)
(4)
能量方程:

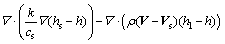 (5)
(5)
上述方程组用于确定金属区基本的物理参数,包括压力p、速度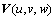 、焓h和温度T。金属材料的性质包括密度ρ、黏性系数μ、比热容c、导热系数k、渗透函数K、惯性系数C和固液态质量分量f,各物性参数的定义见文献[10]。g为重力加速度,J为电流密度矢量,B为磁感应强度矢量,bT为热膨胀系数,下标s和l分别表示固态和液态。Vr=Vl-Vs为两相区内液相与固相的相对速度矢量。模型中,采用连续介质模型[11]处理固液相变边界;能量方程(式(5))以焓函数给出,考虑金属熔化或凝固中吸收或释放潜热的过程。以上方程各项的物理意义见文献[10]。
、焓h和温度T。金属材料的性质包括密度ρ、黏性系数μ、比热容c、导热系数k、渗透函数K、惯性系数C和固液态质量分量f,各物性参数的定义见文献[10]。g为重力加速度,J为电流密度矢量,B为磁感应强度矢量,bT为热膨胀系数,下标s和l分别表示固态和液态。Vr=Vl-Vs为两相区内液相与固相的相对速度矢量。模型中,采用连续介质模型[11]处理固液相变边界;能量方程(式(5))以焓函数给出,考虑金属熔化或凝固中吸收或释放潜热的过程。以上方程各项的物理意义见文献[10]。
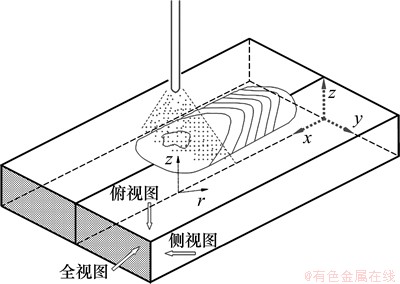
图1 GTAW平板堆焊过程的示意图
Fig.1 Schematic sketch of bead-on-plate GTAW process
1.2 自由表面的跟踪
利用流体体积(VOF)法跟踪自由运动表面[12],该方法引入流体体积分数F(x, y, z, t)表示单位容积内流体所占的比例,满足以下方程:
 (6)
(6)
在计算网格单元内取平均值,即为该单元内金属所占的容积分量。若F=1,则对应的单元格内充满金属;若F=0,则单元格内没有金属;而当F为0~1之间时,则表示金属的自由表面位于该单元格内。这样,可利用F计算自由表面单元及其法线方向,确定熔池的自由表面轮廓。
1.3 边界条件
(1) 沿自由表面垂直方向上的压力p应满足[13]:
 (7)
(7)
其中:parc为电弧压力;g 为表面张力系数; 为自由表面的曲率。电弧压力按下式计算[14]:
为自由表面的曲率。电弧压力按下式计算[14]:
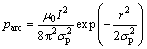 (8)
(8)
其中:μ0为磁导率;I为电流;σp为电弧电压分布参数;r为距电弧中心的距离。
(2) 自由表面切线方向上,温度相关的Marangoni切应力表示为
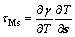 (9)
(9)
其中:s为正切于自由表面的矢量。
(3) 假设热流方向均垂直于工件表面,则工件顶部的温度边界条件为
 (10)
(10)
其中:η为电弧传热效率;uw为电压;σq为电弧热流分布参数。由对流、辐射和蒸发产生的热损失qconv,qrad和qevaq分别为:
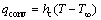 ;
;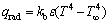 ;
; (11)
(11)
其中:Hev为液-气相变的潜热;W为熔化金属的蒸发率。
(4) 对称面 y = 0,有
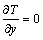 ;
; ;
;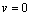 ;
; (12)
(12)
(5) 其他表面,有
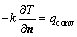 ;
;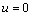 ;
;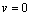 ;
;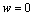 (13)
(13)
其中:n为x,y,或z方向。
1.4 电磁力
假定电场为准静态及电导率为常数,电流方向指向负z方向,电势φ满足以下的麦克斯韦方程[15]:
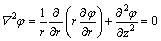 (14)
(14)
在工件的上表面满足以下条件:
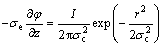 (15)
(15)
其中: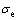 为电导率;
为电导率;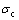 为电流分布参数。获得电势的分布之后,r–z方向上的电流密度Jr。Jz和自感应角向磁场强度Bθ可由下式计算:
为电流分布参数。获得电势的分布之后,r–z方向上的电流密度Jr。Jz和自感应角向磁场强度Bθ可由下式计算:
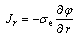 ;
;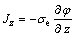 (16)
(16)
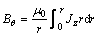 (17)
(17)
因此,式(2)~(4)中电磁力3个方向上的分量由下式计算:
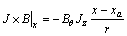 ;
;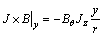 ;
;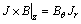 (18)
(18)
2 数值方法
对控制方程式(1)~(5)及边界条件进行迭代计算。在每一时间步长内:(1) 更新参数计算电流连续性方程(式(14)),获得该时刻的电流和电磁力分布;(2) 更新自由表面上的作用力以及热流强度分布,计算动量和能量方程(式(2)~(5));(3) 解VOF方程(式(6)),获得新的金属自由表面形状,更新计算区域各单元内的物性参数和边界条件;(4) 更新时间并将电弧中心移至新的位置,返回至步骤(1)重复上述过程,直至计算结束。
计算区域x×y×z = 300 mm×30 mm×10 mm。由于计算区域沿x–z平面对称,实际中仅计算一半区域,网格数为610×76×82。由于熔池区域随电弧沿焊接方向移动,所以,计算中使用了自适应的非均匀网格,使熔池附近具有更密的网格。计算中平均时间步长为10-4 s。
3 计算结果与讨论
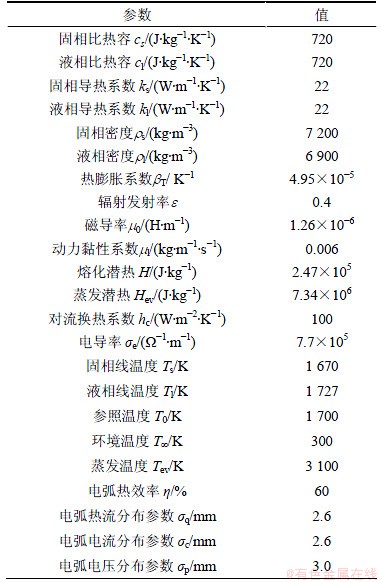
模拟脉冲电流方式下的GTAW焊接过程;同时,计算连续电流下的情形作为比较。如图1所示,工件为304L不锈钢平板(长300 mm,宽30 mm,厚6 mm),钨极焊丝连同电弧沿x轴正方向匀速移动。表1列示为304L不锈钢的物性和计算所需的其他参数。如未特殊说明,连续电流为130 A,电压为12.2 V[1];脉冲电流下峰值电流Ip = 200 A(电压12.5 V),基值电流为Ib=42 A(电压11.2 V),脉冲频率f包括4个等级(分别为1,2,5和10 Hz),占空比为0.55。焊接速度为va=3.4 mm/s。为避免可能的末端影响,焊接从x=10.0 mm处开始;电弧点燃时刻设为t = 0 s。
表1 304L不锈钢的热物性和计算所需的其他参数
Table 1 Thermophysical properties of 304L stainless steel and other parameters
3.1 熔池行为及焊缝成形过程
图2所示为连续电流下,不同时刻工件内温度和熔融金属速度分布的侧视图(y=0)。在电弧作用下,熔池的表面发生严重的变形,在电弧中心处形成1个凹坑。图2(a)和(b)中,液相线温度(T=1 727 K)和固相线温度(T=1 670 K)被标出。与固相区相比,熔池内的等温线形状因熔融金属的强烈对流而发生严重变形。与t=2.00 s时的情况相比,t=3.01 s 时的熔池面积和深度较大。这是因为随着焊接的进行,熔化的金属增加,熔池逐渐变大,直到工件的熔化与凝固速率达到平衡。图2(c)和(d)中上表面由粗实线标出,图中仅画出1/3的网格点数据以增加流场速度矢量的可读性。在凹坑的左侧,熔池表面形成一个从熔池中心向x轴负方向的扩散波,于是,在熔池的尾部积聚大量的高温液态金属。熔池前端的流体向前移动,速度相对较低。两相区(1 670<T<1 727 K)内几乎没有流动。上述流体流动的模式主要是电弧压力、电磁力、表面张力和重力共同作用的结果。电弧压力具有高斯分布,在电弧中心推动流体向下向外流动,是使熔池表面变形的主要原因。t=2.00 s和3.01 s 时的温度和速度分布非常相似,熔池的变形和凝固是一个连续过程,熔池凝固后的焊缝表面基本为平的,这与相关的实验结果相一致[3]。
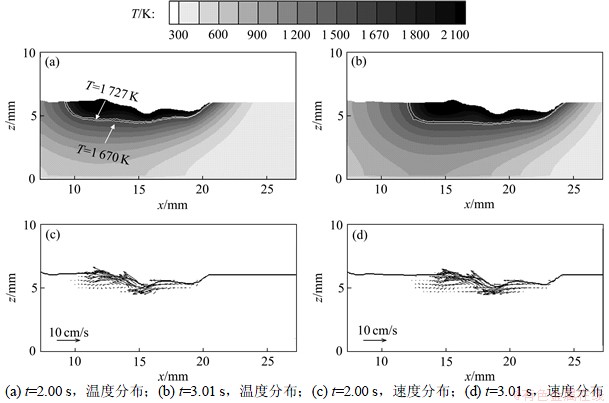
图2 连续电流下,工件内温度和速度的分布侧视图
Fig.2 Side views of temperature distributions and velocity distributions under continuous current
图3和图4所示为脉冲电流f=1 Hz下,t为2.00 s和3.01 s 时,工件内温度和熔融金属速度分布变化的侧视图(y=0)。从图3和图4可见:当t=2.00 s时,基值电流作用在熔池表面,熔池内高温区域较窄、速度较低,表面变形较小;当t=2.01~2.55 s时,电流处于峰值,作用于熔池的热流和电弧压力显著增加,熔池表面严重变形,熔池面积和深度不断增加,此时,速度和温度分布与图2中所示的情形类似,但熔池面积更大、速度更高。由于高温流体的向后传播,大部分高温液态金属积聚在熔池尾部;当t=2.56~3.00 s时,电流转为基值,作用在熔池的热流和电弧压力迅速降低,进入熔池的热量减少,温度降低,熔池面积和深度逐渐减小。在重力和表面张力的作用下,部分流体向前回流而填平凹坑,熔池表面趋于平坦。因此,由于脉冲电流引起的热流和电弧压力等的波动,导致上述的熔池周期性振荡。
当t=2.00 s时,熔池左侧的凝固焊缝表面上已形成1个凸起的焊波,熔池内的液体高度与凝固的焊缝顶部齐平。当t=2.01 s时,电流转为峰值,电弧压力增加,在电弧中心处形成1个凹坑,熔池内的速度和温度均显著增加。当t=2.01~2.55 s时,由于质量守恒,凹坑周围的流体被激起,产生由电弧中心向外且向上的流体流动。其中,大量的流体向后流动,液态熔池尾部表面的高度上升,其最高点远高于波纹顶部。随着焊接的进行,电弧向前移动,熔池尾部的凝固随之进行,导致液相线温度和固相线温度由左向右移动。当t=2.56~3.00 s时,在基值电流下,电弧压力减小,被激起的流体回落趋于填平凹坑;同时,液态金属冷却和凝固速度增大。当t=2.56 s 时,熔池尾部的一部分金属在回落前即被凝固(处于固体区或固液两相区内),形成焊缝波纹的波峰。当t=3.00 s 时,波纹被完全凝固。当t=3.01 s时,液相线移动到新的位置,处于低于波纹低谷的位置处。此时,电流变为峰值,熔池内流体温度和速度增加,熔池尾部液面升高;熔池的形状、温度分布和流动模式与 t=2.01 s时的情形类似。以上为由脉冲电流引起的熔池周期性振荡的循环,周期为1.0 s,也是焊缝波纹形成的1个周期循环,与脉冲频率1 Hz一致。综上所述,脉冲电流周期性的变化引起熔池的振荡和凝固速率波动,造成脉冲GTAW焊缝表面形成焊波。而连续GTAW中的电流恒定,不会引起熔池周期性的振荡,因此,不会形成焊缝波纹。
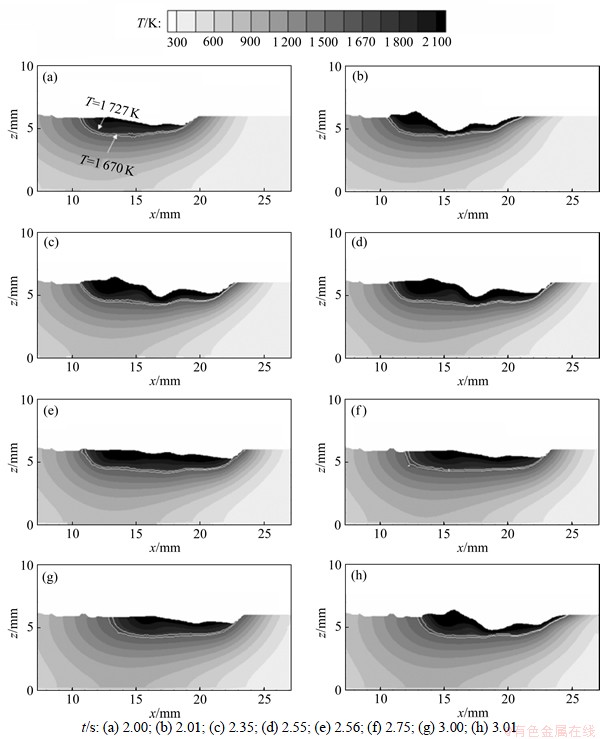
图3 脉冲电流(f=1 Hz)下,工件内温度的变化侧视图
Fig.3 Side views of temperature distributions under pulsed current (f=1 Hz)
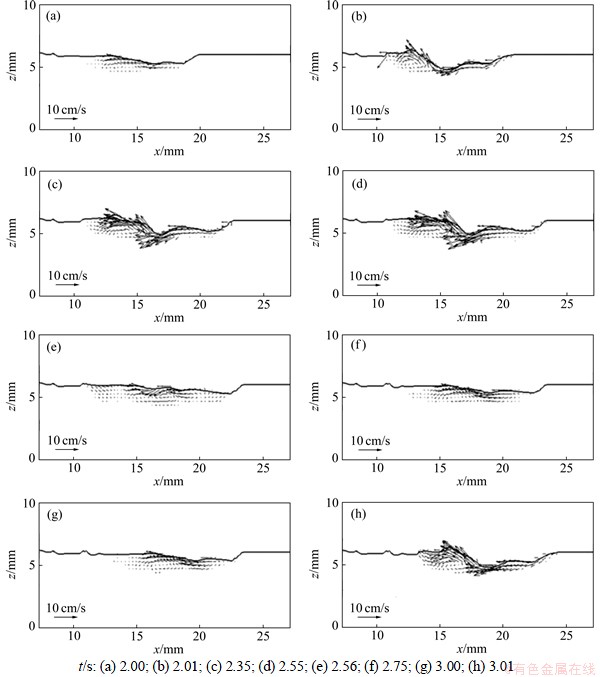
图4 脉冲电流(f=1 Hz)下,工件内速度分布的变化侧视图
Fig.4 Side views of velocity distributions under pulsed current (f=1 Hz)
3.2 脉冲电流频率对焊波的影响
图5和图6所示为脉冲电流频率对温度、熔池形状和焊波的影响,其他焊接参数保持相同。从图5和图6可见:在高脉冲电流频率下,熔池内的对流和混合更强烈,焊波的高度和间距更小。f=1,2,5和10 Hz时的焊波平均高度分别为0.40,0.36,0.30和0.20 mm,平均间距分别为3.40,1.50,0.61和0.31 mm。这是由于脉冲频率增加,导致熔池周期性的振荡频率增加且沿焊接方向上的凝固速率减小,焊波间距和高度减小。
3.3 与实验结果的比较
图7所示为相同条件下脉冲GTAW熔池完全凝固后焊缝表面形状的计算结果和实验结果[3]。焊接条件为:Ip/Ib=185/48 A,占空比 0.55,f =1 Hz,Va=3.4 mm/s;计算中,焊接时间为 6.00 s。发现两者的焊缝表面形状相似,焊波呈现规则的弧形;计算得到的焊波平均间距为3.4 mm,与实验测得结果(约3.46 mm)非常接近。
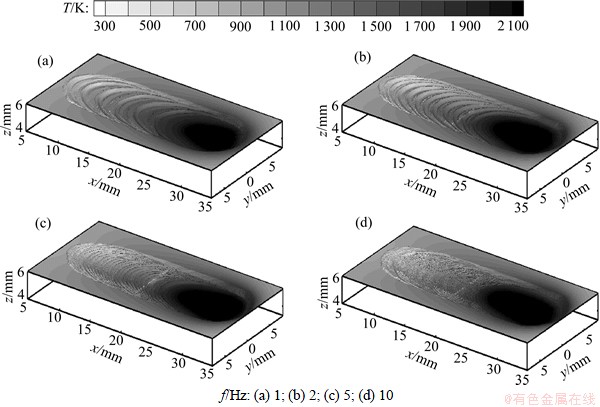
图5 脉冲电流频率对焊波的影响(三维焊缝形状)
Fig.5 Effect of pulsed current frequency on weld wave
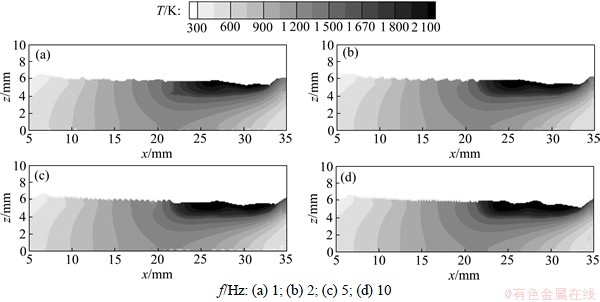
图6 脉冲电流频率对焊波的影响(温度分布侧视图)
Fig.6 Effect of pulsed current frequency on weld wave

图7 脉冲GTAW焊缝表面形状的比较[3]
Fig.7 Comparison of weld bead shape in pulsed GTAW[3]
4 结论
(1) 建立了脉冲GTAW的三维非稳态数学模型,获得不同电流方式下熔池内瞬态速度和温度分布的熔池输运现象。在连续电流下,熔池的形态变化和凝固为连续的过程,不会产生焊波。在脉冲电流下,电流强度交替出现峰值和基值,造成进入熔池的热流以及电弧压力和电磁力等出现周期性的波动,从而引起熔池出现周期性的振荡和凝固速率变化,因此,在焊缝表面产生弧形的焊波。
(2) 模拟结果与实验结果吻合较好。脉冲电流频率增加,导致熔池周期性的振荡频率增加且沿焊接方向上的凝固速率减小,焊波间距和高度减小。
参考文献:
[1] O’Brien R L. Welding handbook (vol. 2)[M]. 8th ed. American Welding Society, 1991: 207-208.
[2] 中国机械工程学会焊接学会编. 焊接手册(第1卷): 焊接方法及设备[M]. 3版. 北京: 机械工业出版社, 2007: 128-129.
Welding Institute of Chinese Mechanical Engineering Society. Welding handbook (vol. 1): Welding method and equipment[M]. 3rd ed. Beijing: China Machine Press, 2007: 128-129.
[3] Lothongkum G, Chaumbai P, Bhandhubanyong P. TIG pulse welding of 304L austenitic stainless steel in flat, vertical and overhead positions[J]. Journal of Materials Processing Technology, 1999, 89/90: 410-414.
[4] Ravisankar V, Balasubramanian V. Optimising pulsed current TIG welding parameters to refine the fusion zone[J]. Science and Technology of Welding & Joining, 2006, 11(11): 57-60.
[5] Giridharan P K, Murugan N. Optimization of pulsed GTA welding process parameters for the welding of AISI 304L stainless steel sheets[J]. International Journal of Advanced Manufacturing Technology, 2009, 40(5/6): 478-489.
[6] Mishra S, Lienert T J, Jobnson M Q, et al. An experimental and theoretical study of gas tungsten arc welding of stainless steel plates with different sulfur concentrations[J]. Acta Materialia, 2008, 56(9): 2133-2146.
[7] Kim W H, Na S J. Heat and fluid flow in pulsed current GTA weld pool[J]. International Journal of Heat and Mass Transfer, 1998, 41(21): 3213-3227.
[8] 武传松, 郑炜, 吴林. 脉冲电流作用下TIG焊接熔池行为的数值模拟[J]. 金属学报, 1998, 34(4): 416-422.
WU Chuansong, ZHENG Wei, WU Lin. Numerical simulation of TIG weld pool behavior under the action of pulsed current[J]. Acta Metallurgica Sinica, 1998, 34(4): 416-422.
[9] 赵明, 武传松, 胡庆贤. TIG焊接熔透熔池形状和表面变形的数值模拟[J]. 机械工程学报, 2006, 42(10): 203-208.
ZHAO Ming, WU Chuansong, HU Qingxian. Numerical simulation of penetrated weld pool geometry and surface deformation in TIG welding[J]. Chinese Journal of Mechanical Engineering, 2006, 42(10): 203-208.
[10] Rao Z H, Zhou J, Liao S M, et al. Three–dimensional modeling of transport phenomena and their effect on the formation of ripples in gas metal arc welding[J]. Journal of Applied Physics, 2010, 107(5): 054905-14.
[11] Diao Q Z, Tsai H L. Modeling of solute redistribution in the mushy zone during solidification of aluminum-copper alloys[J]. Metall Trans A, 1993, 24(4): 963-973.
[12] Torrey M D, Mjolsness R C, Stein L R. NASA–VOF3D: A three–dimensional computer program for incompressible flows with free surfaces[R]. Los Alamos: Los Alamos National Laboratory, 1987: 4-5.
[13] Kothe D B, Mjolsness R C. Ripple: a new model for incompressible flows with free surfaces[R]. Los Alamos: Los Alamos National Laboratory, 1991: 4-5.
[14] Tsai N S, Eagar T W. Distribution of the heat and current fluxes in gas tungsten arcs[J]. Metallurgical and Materials Transactions B, 1985, 16 (4): 841-846.
[15] Hu J, Tsai H L. Heat and mass transfer in gas metal arc welding, PartⅠ: The arc[J]. International Journal of Heat and Mass Transfer, 2007, 50(5/6): 833-846.
(编辑 邓履翔)
收稿日期:2012-10-04;修回日期:2012-12-12
基金项目:中央高校基本科研业务费专项资金资助项目(2011QNZT097)
通信作者:饶政华(1977-),男,江西鹰潭人,博士,副教授,从事材料加工过程传热、传质分析的研究;电话:0731-88879863;E-mail: raoz@csu.edu.cn