基于高斯滤波法剪切作用下节理表面形貌演化

蒋喆，曹平，范祥，何云，范文臣

(中南大学 资源与安全工程学院，湖南 长沙，410083)

摘要：选取2类岩石节理试样进行3种法向应力条件下的剪切试验，采用高精度三维激光形貌仪Talysurf CLI 2000获取节理表面三维形貌图，并基于高斯滤波法，将原始节理表面分离为波纹度表面与粗糙度表面，通过计算节理表面粗糙度系数比(S)与表面磨损度(D_s)，研究剪切作用下节理表面形貌变化规律。结果表明：起伏体的破坏使得波纹度表面和粗糙度表面的整体粗糙程度均出现明显下降；波纹度表面磨损度随着法向应力的增大而增大，而粗糙度表面磨损度在首次剪切后最大，且大于波纹度表面磨损度；法向应力较低时原始节理表面形貌变化主要取决于粗糙度表面，法向应力较高时节理表面形貌变化则由波纹度表面控制。

关键词：岩石节理；剪切试验；高斯滤波；节理表面形貌；波纹度表面；粗糙度表面

中图分类号：TU45          文献标志码：A         文章编号：1672-7207(2014)06-1975-08

Evolution of joint morphology subjected to shear loads based on Gaussian filtering method

JIANG Zhe, CAO Ping, FAN Xiang, HE Yun, FAN Wenchen

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: Two kinds of rock joint samples underwent a monotonic shear test under three different normal stresses. Three-dimensional laser topography instrument Talysurf CLI 2000 was used to acquire 3D joint surface morphology. Based on Gaussian filtering method, the original joint surfaces were divided into waviness surface and roughness surface, which can be analyzed separately. Then, the morphological evolution of joint surface subjected to shear loads was investigated by analyzing joint specific roughness coefficient (S) and joint surface degradation degree (D_s) quantitatively. The experimental results show that the entire roughness of waviness surface and roughness surface has a clear decline due to the damage of asperities during the shearing process. The degradation degree for waviness surface increases gradually with the increase of normal stress, while the maximum degradation degree for roughness surface appeares after the first shear test and it is greater than the degradation degree for waviness surface. The morphological evolution of original joint surface is mainly dominated by roughness surface and waviness surface, respectively, under low and high normal stresses.

Key words: rock joint; shear test; Gaussian filtering; joint surface morphology; waviness surface; roughness surface

岩体中节理面的存在破坏了岩体的连续性和完整性，其力学特性和变形特性对岩体工程的设计和施工都有着重要影响。岩石节理在剪切过程中，节理表面的起伏体会被磨损、压碎或剪断。随着剪切次数增加，节理表面的粗糙程度不断退化，其剪切强度等力学参数也相应劣化。岩石力学工作者长期的研究表明，节理表面的形貌特征与节理岩体的力学特性密切相关^[1-2]。国内外学者对此做了大量的研究，如Grasselli等^[3-4]、Gentier等^[5]和曹平等^[6]分别研究了节理表面微元有效剪切倾角、凸起体的尺寸与分布以及节理表面轮廓平均角与节理抗剪强度的依存关系。完整节理的表面形貌由较大尺寸的一阶起伏体和大量小尺寸的二阶起伏体叠加而成^[1]。本文作者将仅含一阶起伏体的节理表面称为波纹度表面，将仅含二阶起伏体的节理表面称为粗糙度表面。实际上，现阶段的研究工作大多并未区分一阶起伏体和二阶起伏体，或者针对的是只含有一阶起伏体的节理表面，仅有少数学者考虑了二阶起伏体对整个表面形貌的影响。其中，Belem等^[7]定义了5个三维形貌参数，定量描述了节理表面的波纹度与粗糙度特征。Homand等^[8-10]在文献[7]的基础上分析了剪切过程中节理表面的磨损特征，提出了表征节理表面累积磨损程度的参数，并建立了相应的节理峰值剪切强度准则。Lee等^[11]采用花岗岩和大理岩节理试样进行循环剪切试验，发现二阶起伏体对节理剪切力学行为影响更加显著，节理表面磨损包含波纹度表面的磨损与粗糙度表面的磨损，据此建立了含有二阶起伏体的循环剪切本构模型。Yang等^[12-13]利用傅里叶变换重构含二阶起伏体的节理试样，探讨了剪切过程中节理表面二阶起伏体对节理磨损面积、峰值剪切强度、残余强度以及分形维数的影响。朱小明等^[14-15]研究了不同二阶起伏体与节理剪切强度、变形特征的相互关系。然而，上述研究工作多集中在节理表面的粗糙特性对节理力学特性的影响方面，尚未有学者研究经历剪切后节理波纹度表面与粗糙度表面的形貌变化特征。本文作者选取两类岩石制成节理剪切试样，进行不同法向应力下的剪切试验，采用先进的高精度非接触式三维激光形貌仪Talysurf CLI 2000对节理表面进行扫描，获取剪切前后节理表面三维形貌数据。与此同时，高斯滤波^[16]在表面测量领域的应用提供了研究表面粗糙特性的新方法，基于高斯滤波分析法，将原始节理表面分离为波纹度表面与粗糙度表面，分别研究剪切作用下节理表面波纹度与粗糙度的变化特征，提出了表征节理表面磨损程度的参数D_s，并定量计算了每次剪切过程中节理表面的磨损度。

1  试验概述

1.1  试样制备

试验所用岩样采自甘肃金川矿区，岩性分别为花岗岩和大理岩，将岩样加工成适合的尺寸，采用劈裂法制作多组新鲜节理试样。同时，制作尺寸为250 mm×200 mm×150 mm(长×宽×高)的模具，选用42.5R快硬水泥浇筑水泥砂浆固定节理试样，浇筑时上、下两模具间预留10 mm高的剪切间隙，在常温下养护28 d，达到预定抗压强度即可。

1.2  试验设备简介

1.2.1  RYL-600岩石剪切流变仪

剪切试验在RYL-600岩石剪切流变仪上完成。试验过程中的加卸载均由计算机控制系统完成。与RYL-600相配套的数据记录软件Test记录试验过程中的剪切位移、剪切应力等参数。

1.2.2  Talysurf CLI 2000三维激光形貌仪

采用英国Taylor Hobson公司生产的Talysurf CLI 2000三维激光形貌仪获取节理试样的形貌参数。该设备扫描精度可达0.05 μm，内置数据分析软件TalyMap Gold 5.0可对形貌数据进行处理与分析。激光扫描测量遵循三角光学原理，通过光电转换系统将节理表面形貌的起伏变化转换成与测量距离成比例的电流信号，再将电流信号经过放大和模数转换，即可实现节理表面形貌的获取、存储、处理和三维可视化。

1.3  试验过程

进行剪切试验时，先在节理试样的垂直方向以50 N/s的速率施加法向应力，达到预设法向应力后保持法向应力恒定，然后在水平方向以0.01 mm/s的速率对上半部分试样施加剪切力，每次试验的最大剪切位移均设置为20 mm，达到预设剪切位移后进行卸载，完成剪切试验。同一块试样依次采用3，5和8 MPa的法向应力进行三次剪切试验。每次剪切试验前后对节理表面进行扫描，扫描点间距设定为20 μm。由于采用非接触式激光扫描，不会对节理表面产生损伤，获取的节理形貌参数能真实反映节理粗糙程度。

2  节理表面高斯滤波

2.1  节理表面高斯滤波

岩石节理表面极不规则，Yang等^[12-13]认为岩石节理表面轮廓可以分解为一系列正弦或者余弦函数，通过不同波长、频率、幅值以及相位的谐波函数叠加可以模拟节理表面的起伏形态，且叠加的谐波次数越高，越能反映节理表面二阶起伏度，与节理表面的重合度也越高。夏才初等^[17]对实测节理表面形态的周期性研究结果发现，节理表面形貌包含着不同频率、幅值及相位组成的波纹度和粗糙度，波纹度的特点是起伏缓，幅值大，在频率域里属于低频分量，粗糙度的特点是起伏陡，幅值小，属于节理表面的高频分量。可以看出，节理表面包含了多种频率成分，尺寸较大的一阶起伏体组成的表面波纹度属于低频部分，而由随机不规则的二阶起伏体组成的表面粗糙度则属于高频成分，节理表面形貌实际由低频波纹度和高频粗糙度叠加而成，这反映出节理表面的复杂性和不规则性。采用高斯滤波法分析节理表面形貌，是基于节理表面的波长、频率特征，在频率域内对不同的频率成分进行分离、提取，从而有效地分离出波长较长的表面波纹度以及波长较短的表面粗糙度，进而能分别定量的研究波纹度表面和粗糙度表面的形貌特征。

高斯滤波是以高斯函数为转换权函数，构成一个在频率域的低通滤波器，高斯权函数进行傅里叶变换后可得到滤波器的传输特性。节理表面高斯滤波过程如下：将节理表面采样数据与高斯权函数进行一次卷积运算，所得结果即为节理表面频率成分低于滤波器截止频率的低频信号，将此低频形貌信号提取出来，作为节理表面的波纹度，则节理表面粗糙度即为原始节理表面与通过低通滤波器的表面波纹度成分之差。高斯滤波运算的权函数^[17]为

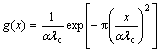          (1)

高斯滤波器的转换函数为g(x)的傅里叶变换形式：

   (2)

式中：λ为波长，λ_c为滤波器截止波长，当λ=λ_c时，高斯滤波器的传输比例为50%，即G(λ)=0.5，则有定值。

将节理表面采样数据z(ξ)与高斯权函数进行一次卷积运算：

         (3)

所得w(x)即为节理表面的低频波纹度信号，显然，节理表面粗糙度r(x)即为

r(x)=z(x)-w(x)               (4)

高斯滤波过程实际上就是滤波器权函数窗在原始表面上不断移动平均的结果，高斯滤波运算后，即可实现节理波纹度表面w(x)与节理表面粗糙度表面r(x)的分离。

2.2  高斯滤波后节理表面形貌分析

为保证一阶起伏体尺寸比二阶起伏体尺寸大1个数量级，本文取2.5 mm为高斯滤波器的截止波长。图1和图2所示分别为2组典型的未经剪切的节理试样在高斯过滤前、后的三维形貌。使用盒维数法对高斯过滤后的节理表面进行分形分析，其分形维数如表1所示。

表1  高斯过滤前后节理表面分形维数

Table 1  Fractal dimension of joint samples before and after Gaussian filtering

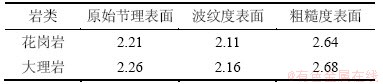
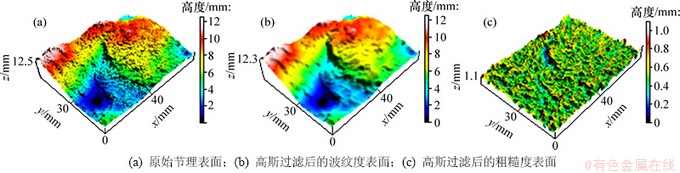
图1  花岗岩节理试样高斯过滤前后节理表面三维形貌图

Fig. 1  3D surface morphologies of granite joint sample before and after Gaussian filtering

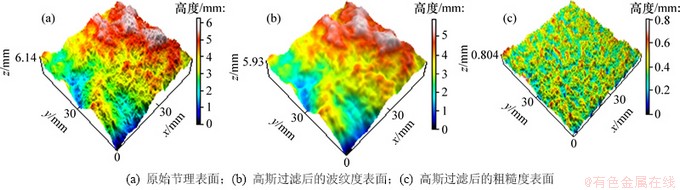
图2  大理岩节理试样高斯过滤前后节理表面三维形貌图

Fig. 2  3D surface morphologies of marble joint sample before and after Gaussian filtering

由图1、图2和表1可以看出：高斯过滤前的原始节理表面粗糙，褶皱明显。高斯过滤后的波纹度表面光滑、圆润，相比于原始表面，分形维数降低，褶皱明显减少，同时，波纹度表面的起伏趋势与原始节理表面相同，在高度特征方面较原始表面稍有减小；高斯过滤后的粗糙度表面已看不出较大的起伏趋势，表面布满的是尺寸较小且粗糙的二阶起伏体，其高度变化幅度较小，但坡度较陡，表面精细结构丰富，分形维数相对于原始表面有显著增加。高斯过滤可以有效的分离节理表面一阶起伏体和二阶起伏体。此外，由表1可看出：分形维数与节理表面频率成分有关，分形维数越大，表明节理表面含有高频的二阶起伏体较多，节理表面越不规则；分形维数小，则表明节理表面波长较长，表面形貌简单。

3 节理表面三维粗糙参数

随着节理表面形貌特征研究不断深入，基于轮廓线的二维粗糙参数已难以满足研究的要求，选取合适的三维评定参数成为研究节理表面三维形貌的前提。本文选取Belem等^[7]提出的粗糙度系数比S作为评定节理表面粗糙程度的三维粗糙参数，同时基于剪切前后S的变化，提出了表征节理表面损伤程度的参数，即节理表面磨损度D_s。

3.1 粗糙度系数比S

节理表面粗糙度系数比S表示节理表面相对于水平面的粗糙程度，用以表征节理表面的复杂情况。以节理实际表面面积A_t相对于节理名义表面面积A_n(即节理表面在水平面上的投影面积)的增量ΔA与A_n的比表示：

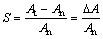            (5)

S越大，说明节理表面越粗糙，表面情况也越复杂；而当S=0时，表示节理表面完全平整。波纹度表面和粗糙度表面的粗糙度系数比分别用S_w和S_r表示。

3.2 节理表面磨损度D_s

对于剪切过程中节理表面形貌的磨损情况，文献[14-15]只进行了定性的描述性研究，并未从定量的角度计算节理表面的磨损程度，而Homand等^[8]提出的磨损参数，则更侧重于表征循环剪切过程中节理表面的累积磨损程度，为了更直观地计算每一次剪切作用对节理表面造成的损伤，本文将每一次剪切后粗糙度系数比相对于剪切前粗糙度系数比降低的比值D_s作为新的表征节理表面损伤程度的参数，即表面磨损度D_s：

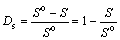           (6)

式中：S为当前节理表面粗糙度系数比；S^o为每一次剪切试验前节理表面粗糙度系数比。

由式(5)和(6)可得：

          (7)

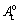式中：和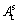分别为每次剪切试验前、后节理实际表面面积，A_d为该次剪切的磨损面积。

若剪切试验后D_s=0，则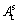=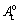，表明剪切过程中节理表面没有磨损，剪切并未造成节理表面粗糙程度的退化；若剪切试验后D_s=1，则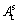=A_n，表明剪切过程中节理表面的起伏体被完全磨平，剪切后的节理表面是完全平整的水平面，剪切对节理表面损伤最为严重。波纹度表面和粗糙度表面的表面磨损度分别用D_w和D_r表示。

4 试验结果及分析

4.1 剪应力-剪切位移曲线分析

图3所示为2种岩性的典型试样在不同法向应力下的剪应力-剪切位移曲线，由图3可知：在剪切试验初期，剪应力随剪切位移迅速增加到峰值，且呈线性增长形式，此时节理表面表现出弹性特性。

当σ_n=3 MPa时，剪应力-剪切位移曲线波动变化更明显。分析表明，节理表面的起伏体呈相互咬合状态时，能提供较大的抗剪强度，致使剪应力上升；当剪应力随剪切位移增加到一定值时，强度较低的二阶起伏体尖端被剪断，导致剪应力下降；当节理再次跨越残留的二阶起伏体时，重新产生咬合使得剪应力再次上升，直至二阶起伏体完全从根部剪断、磨平为止；当σ_n=8 MPa时，剪应力—剪切位移曲线出现幅度较大的波形起伏变化，这正是因为在前两次剪切过程中，能提供剪切阻力的二阶起伏体被大量剪断、磨平，且第3次剪切时法向应力较大，节理难以发生剪胀扩容现象，导致尺寸较大的一阶起伏体发生剪断破坏，从而使得剪应力波动幅度变大。

由图3还可看出：随着法向应力的增加，节理峰值剪切应力呈非线性增长趋势。显然，经历剪切后的节理表面更加平滑，剪切过程中可提供的摩擦阻力的起伏体变少，节理表面咬合程度降低，势必导致节理峰值剪切强度增幅变小。

4.2 节理表面三维粗糙参数变化规律

每次剪切试验后节理表面面积及节理表面的三维粗糙参数如表2所示。从表2可知：每一次剪切试验后，节理实际表面面积A_t均出现明显减少，S降低，说明剪切过程中节理表面的起伏体被磨平、压碎或剪断，微小褶皱被碾平，经历剪切后的节理表面变得更为光滑、平整，使得节理实际面积减小。同时，第1次剪切试验后表面积减少最多，说明第1次剪切给节理表面造成的损伤程度最大，磨损最严重。经历3次剪切作用后，花岗岩节理试样的实际表面面积总共减少了7.336%，S降幅为25.50%，而大理岩节理试样则减少4.040%，S降幅为19.25%，说明剪切过程对花岗岩节理试样造成的损伤更严重，其表面粗糙程度退化越严重。

4.3 节理波纹度表面与粗糙度表面形貌变化规律

运用高斯滤波法分离出节理波纹度表面及节理粗糙度表面，图4所示为每次剪切后大理岩节理试样的波纹度表面及粗糙度表面三维形貌图。

结合图3和图4可以看出：第1次剪切后节理粗糙度表面高度下降最大，二阶起伏体的尖端被大量剪断，此后2次剪切粗糙度表面高度继续下降，但幅度明显减小，第3次剪切后的粗糙度表面变化已不再明显。前2次剪切过后，节理波纹度表面形貌只在高度较高处变化较为明显，其表面高度逐渐下降，而第3次剪切后，节理中部也出现了明显的破坏区域，高度下降幅度也最大。

4.4 节理波纹度表面与粗糙度表面三维粗糙参数变化规律

分别计算节理波纹度表面及粗糙度表面的粗糙度系数比与表面磨损度。本文以未经历剪切的节理表面粗糙度系数比为基准，对每次剪切试验后的粗糙度系数比进行归一化处理。经历3次剪切后花岗节理试样和大理岩节理试样的三维粗糙参数变化曲线如图5所示。由图5可以看出：

(1) 经过3次剪切，节理表面S，S_w和S_r呈现整体下降趋势，说明无论是原始节理表面还是高斯过滤后的波纹度表面及粗糙度表面，在经历剪切作用后表面粗糙程度都出现全面降低，在剪切过程中起伏体的磨损使得节理表面凹凸起伏程度下降，其表面形貌趋于平缓。

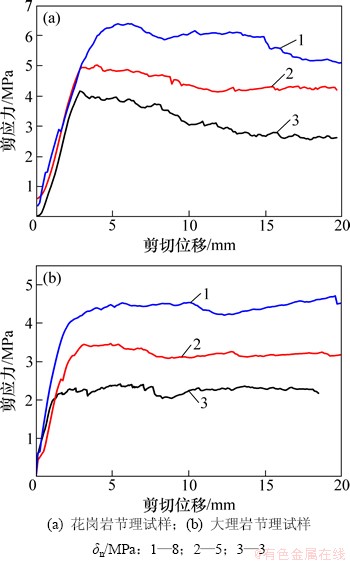
图3  剪应力-剪切位移曲线

Fig. 3  Curves of shear stress-shear displacement

表2  剪切前后节理试样三维粗糙参数

Table 2  Three-dimensional roughness parameters of joint samples before and after shear tests

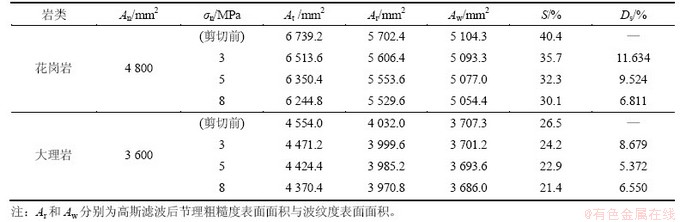
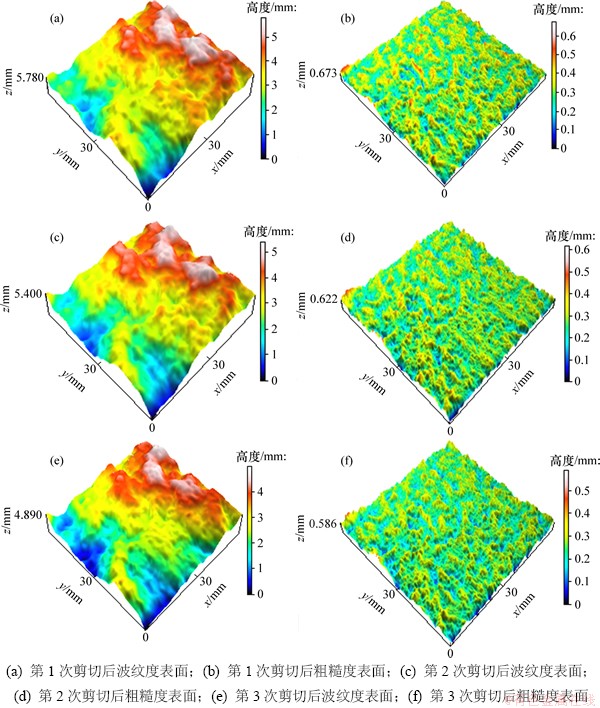
图4  每次剪切后大理岩节理试样波纹度表面及粗糙度表面三维形貌图

Fig. 4  3D waviness surface and roughness surface morphologies of marble joint sample after each shear test

(2) 节理波纹度表面的S_w变化曲线逐渐变陡，而粗糙度表面的S_r变化曲线则趋于平缓。这表明随着法向应力的增加，波纹度表面粗糙程度下降越来越快，而粗糙度表面的粗糙程度下降逐渐减弱，符合图4变化规律。

(3) 波纹度表面的D_w在整体上呈现出不断上升的趋势，而对于粗糙度表面，第1次剪切后的D_r明显高于此后2次剪切的D_r，同时也高于D_w。结合图4分析认为，一阶起伏体和二阶起伏体在剪切作用下破坏模式的不同是导致波纹度表面和粗糙度表面变化不一致的原因。对于粗糙度表面，二阶起伏体强度较小，在第1次剪切过程中大部分即被磨平、剪断，使得此后2次剪切过程中的D_r较第1次剪切的小；而一阶起伏体的强度较高，第1次剪切时法向应力较低，因此受损并不严重，随着法向应力继续增加，剪应力的增长使得一阶起伏体的损伤加剧，导致波纹度表面磨损度不断增加。此外，由图5(c)和5(d)可以看出：D_w与D_r变化曲线都有1个交叉点，说明当法向应力大于一定的限值时，波纹度表面磨损度开始超过粗糙度表面磨损度，花岗岩节理试样的限值约为5 MPa，大理岩节理试样约为3 MPa。

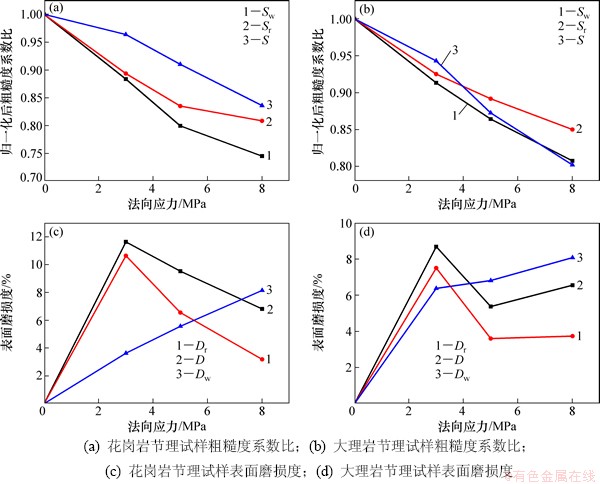
图5  节理表面三维粗糙参数变化

Fig. 5  Variations of three-dimensional roughness parameters for joint surfaces

(4) 当法向应力为3 MPa时，D与D_r更为接近；随着法向应力的增加，D与D_r的差值逐渐增大，而D_s与D_w的差则逐渐减小。与之类似地，S，S_w和S_r也出现相同的变化规律。这表明：在法向应力较小时，原始节理表面的粗糙特性更多由粗糙度表面决定，二阶起伏体的磨损在节理表面的磨损中占主要地位，随着法向应力的增加，一阶起伏体的损伤加剧致使节理表面形貌变化规律主要由波纹度表面控制。

5  结论

(1) 经历剪切作用后，节理实际表面面积减少，粗糙度系数比S降低，节理波纹度表面和粗糙度表面的整体粗糙程度均出现明显下降。

(2) 表面磨损度D能很好地表征节理表面损伤程度，节理波纹度表面的D_w和粗糙度表面的D_r变化不同且变化趋势不一致，这与起伏体的破坏模式密切相关。一阶起伏体的破坏随法向应力的增大而增大，导致波纹度表面磨损度D_w逐渐增加；二阶起伏体则在首次剪切后即被大量剪断、磨平，导致粗糙度表面磨损度D_r先高后低，且第1次剪切后D_r大于D_w。

(3) 当法向应力较低时，原始节理表面与粗糙度表面的形貌变化规律更为相似，节理表面的损伤趋势主要取决于二阶起伏体的磨损程度；随法向应力的增加，一阶起伏体的损伤成为控制节理表面磨损特征的主要因素。

参考文献：

[1] Parton F D. Multiple modes of shear failure in rock[C]//Proceedings of the 1st Congress of the International Society for Rock Mechanics. Lisbon, Portugal: ISRM, 1966: 509-513.

[2] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics and Rock Engineering, 1977, 10(1/2): 1-54.

[3] Grasselli G, Wirth J, Egger P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 789-800.

[4] Grasselli G. Manuel Rocha medal recipient–shear strength of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering, 2006, 39(4): 295-314.

[5] Gentier S, Riss J, Archambault G, et al. Influence of fracture geometry on sheared behavior[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1/2): 161-174.

[6] 曹平, 范祥, 蒲成志, 等. 节理剪切试验及其表面形貌特征变化分析[J]. 岩石力学与工程学报, 2011, 30(3): 480-485.

CAO Ping, FAN Xiang, PU Chengzhi, et al. Shear test of joint and analysis of morphology characteristic evolution of joint surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 480-485.

[7] Belem T, Homand-Etienne F, Souley M. Quantitative parameters for rock joint surface roughness[J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217-242.

[8] Homand F, Belem T, Souley M. Friction and degradation of rock joint surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geo Mechanics, 2001, 25(10): 973-999.

[9] Belem T, Souley M, Homand F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing[J]. Acta Geotechnica, 2007, 2(4): 227-248.

[10] Belem T, Souley M, Homand F. Method for quantification of wear of sheared joint walls based on surface morphology[J]. Rock Mechanics and Rock Engineering, 2009, 42(6): 883-910.

[11] Lee H S, Park Y J, Cho T F, et al. Influence of asperity degradation on the mechanical behavior of rough rock joints under cyclic shear loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(7): 967-980.

[12] Yang Z Y, Di C C, Yen K C. The effect of asperity order on the roughness of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(7): 745-752.

[13] Yang Z Y, Taghichian A, LI Weichan. Effect of asperity order on the shear response of three-dimensional joints by focusing on damage area[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(6): 1012-1026.

[14] 朱小明, 李海波, 刘博, 等. 含一阶和二阶起伏体节理剪切强度的试验研究[J]. 岩石力学与工程学报, 2011, 30(9): 1810-1818.

ZHU Xiaoming, LI Haibo, LIU Bo, et al. Experimental study of shear strength of joints with first-order and second-order asperities[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1810-1818.

[15] 朱小明, 李海波, 刘博, 等. 含二阶起伏体的模拟岩体节理试样剪切特性试验研究[J]. 岩土力学, 2012, 33(2): 354-360.

ZHU Xiaoming, LI Haibo, LIU Bo, et al. Experimental study of shear characteristics by simulating rock mass joints sample with second-order asperities[J]. Rock and Soil Mechanics, 2012, 33(2): 354-360.

[16] ISO 11562, Geometric product specifications (GPS)—surface texture: Profile method—Metrological characteristics of phase correct filters[S].

[17] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002: 38-39.

XIA Caichu, SUN Zongqi. Engineering rock joint mechanical[M]. Shanghai: Tongji University Press, 2002: 38-39.

(编辑  陈爱华)

收稿日期：2013-08-19；修回日期：2013-11-27

基金项目：国家自然科学基金资助项目(51274249)；中南大学研究生培养创新基金项目(2012cxjd007)

通信作者：曹平(1959-)，男，湖南祁东人，教授，博士生导师，从事岩石力学工程与应用研究；电话：0731-88879263；E-mail：pcao_csu@sina.com