J. Cent. South Univ. (2016) 23: 3356-3364
DOI: 10.1007/s11771-016-3401-9

Sliding-mode control of path following for underactuated ships based on high gain observer
QIN Zi-he(秦梓荷), LIN Zhuang(林壮), SUN Han-bing(孙寒冰), YANG Dong-mei(杨东梅)
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: A nonlinear robust control strategy is proposed to force an underactuated surface ship to follow a predefined path with uncertain environmental disturbance and parameters. In the controller design, a high-gain observer is used to estimate velocities, thus only position and yaw angle measurements are required. The control problem of underactuated system is transformed into a control of fully actuated system through adopting an improved line-of-sight (LOS) guidance law. A sliding-mode controller is designed to eliminate the yaw angle error, and provide the control system robustness. The control law is proved semi-globally exponentially stable (SGES) by applying Lyapunov stability theory, and numerical simulation using real data of a monohull ship illustrates the effectiveness and robustness of the proposed methodology.
Key words: underactuated ship; path following; sliding-mode control; line-of-sight guidance; high gain observer
1 Introduction
Ships undergo a three-degree freedom motion (surge, sway and yaw) under the combined action of powerplants such as propellers, rudders, lateral thrusters. The most difficult part for the path following and trajectory tracking control of an underactuated ship is that only its yaw rate and surge speed are directly driven while its sway speed is not actuated. To reduce the transportation cost, this underactuated drive configuration becomes the most common form in marine ships [1]. Control algorithm studying on the underactuated systems is necessary to insure the sailing safety of underactuated ships and improving the autopilot’s control performance. Therefore, it has received a close attention from many scholars [2-4].
The control methods for underactuated system involve backstepping technique, sliding-mode theory, cascade theory, Lyapunov method, etc. YANG et al [5] considered the uncertain parameters and unknown current in path following of an underactuated unmanned surface vehicle (USV), and put forward a robust control strategy for path following by adopting backstepping technique and parameter adaptive method. DO et al [6] combined the cascade method with Lipschitz projection algorithm and proposed an adaptive methodology for path following of underactuated ships. DING and GUO [7] studied a formation control problem of multi- underactuated system without considering the external disturbance and by using backstepping technique and leader-follower method, the position errors and orientation error are asymptotically stabilized.
In reality, ships are often influenced by environmental disturbances involving wave, wind, and current. Besides, the motion parameters could vary with the load condition of ships. These cases would have negative influence on the autopilot control. Because of the variable structure feature, sliding-mode control has good robustness against uncertainties such as uncertain model parameter, external perturbation, and unmodeled dynamics [8-10]. The sliding-mode can handle the above mentioned adverse effect well. FANG and LUO [11] proposed a sliding-mode controller for ship trajectory tracking and roll-reducing under external random waves. In Ref. [12], heading control with rudder nonlinearity and parametric uncertainties was studied, and a sliding backstepping controller based on parameter adaptive theory was designed. OH and SUN[13] used a LOS based path generator, and made a model predictive control (MPC) for underactuated ship. However, the proposed guidance law for line segments can not be used in tracking curved path.
The ship velocities information is needed in the output feedback control of path following. Nevertheless, for the sake of cutting cost and simplifying mechanism,velocity and yaw rate measuring instruments may not be equipped on ships. Therefore, the path following study on immeasurable velocities is necessary. High-gain observer is capable of using the output to estimate the system output’s derivative term without relying on the mathematical model; therefore, it is extensively used in nonlinear output feedback control [14-15]. FOSSEN and  [16] designed a velocity observer for ship dynamic position (DP) control by using high gain observer theory, and the proposed observer has obtained favorable effect on velocities estimating. DU et al [17] considered external environmental disturbances in motion modeling and by uniting vector backstepping with dynamic surface method, a feedback control law for DP based on high gain observer was proposed. In path following control, higher order nonlinearity is emerged due to the existence of the Coriolis and centripetal matrix. This nonlinearity adds difficulty for observer design and stability analysis. In Ref. [18], the trajectory tracking for ocean vessels in the presence of uncertainties and unknown disturbances was studied. The stable tracking control system is obtained by employing a high-gain observer to estimate the immeasurable states. However, the work was concentrated on fully actuated vessels.
[16] designed a velocity observer for ship dynamic position (DP) control by using high gain observer theory, and the proposed observer has obtained favorable effect on velocities estimating. DU et al [17] considered external environmental disturbances in motion modeling and by uniting vector backstepping with dynamic surface method, a feedback control law for DP based on high gain observer was proposed. In path following control, higher order nonlinearity is emerged due to the existence of the Coriolis and centripetal matrix. This nonlinearity adds difficulty for observer design and stability analysis. In Ref. [18], the trajectory tracking for ocean vessels in the presence of uncertainties and unknown disturbances was studied. The stable tracking control system is obtained by employing a high-gain observer to estimate the immeasurable states. However, the work was concentrated on fully actuated vessels.
In this work, the path following problem of underactuated ship is addressed, with uncertainties and velocities measuring be unavailable. We consider an underactuated ship with parametric uncertainty and disturbed by random wave. A high-gain observer is designed to estimate the velocities using only the position and yaw angle. Considering the path following problem, a robust controller is proposed based on LOS guidance law and sliding-mode control method. By using an advanced LOS method, the heading law is designed for tracking curved lines. The sliding-mode controller is proposed to stabilize the yaw angle error, and deals with the parametric uncertainty and wave disturb, thus giving the control law robustness. Based on Lyapunov stability analysis, the semi-globally exponential stability (SGES) of the original control system is demonstrated. The real data of a monohull ship are used in numerical simulation to demonstrate that the proposed methodology is effective and robust to the parametric uncertainty and environment disturbances.
2 Ship dynamics
In the study of path following, it is conventional to ignore the heave, pitch and roll of the ship, and only motions in surge, sway and yaw axis are considered. Assuming that the ship is symmetric on port and starboard, and the origin of body-fixed coordinate is set on the ship’s center line. For the convenience of observer design, the position and velocities are described into vector form. In the forthcoming sections, the earth-fixed position (x, y) and yaw angle ψ of the ship are expressed as η=(x, y, ψ)T, and the body-fixed velocities are represented as v=(u, v, r)T. Therefore, the equations of motion on a horizontal plane described in Ref. [19-20] can be rewritten as
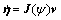 (1)
(1)
 (2)
(2)
where
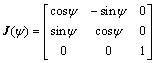 (3)
(3)
J(ψ) is the rotation matrix of ship from body-fixed frame to earth-fixed frame, and M denotes the inertia matrix including hydrodynamic added inertia. C(v) denotes the Coriolis and centripetal matrix and it is caused by the rotation. D denotes the hydrodynamic damping in surge, sway and yaw. τ=(τu, 0, τr)T is the control input, which consists of surge thrust and yaw moment. ξ=(ξu, ξv, ξr)T denotes the disturbances acting on ship hull. M, D and C(v) have the following form respectively.
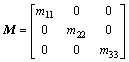 (4)
(4)
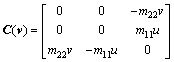 (5)
(5)
 (6)
(6)
Noticing that M and D are both positive definite, and XTC(v)X=0 is confirmed for any X≠0.
To design the controller, we list the following assumptions about measure and wave disturbance.
Assumption 1: The ship is not equipped with velocity measuring instrument, thus only the position and yaw angle are measurable, and there is no delay in signal transmission.
Assumption 2: The disturbance is bounded and  where ξmax is a positive constant.
where ξmax is a positive constant.
In the path following, only the ship to track along a desired path is required, without considering the restrictions of speed and time. Therefore, to simplify the study, we assume that the surge thrust τu is a positive constant instead of setting the surge speed u constant because the former is much more feasible in practice.
3 Controller design
The proposed control system is composed of four units as presented in Fig. 1, and these units are LOS guidance, high gain observer, sliding-mode controller, and ship dynamics. The high-gain observer estimates the ship velocities only using information of ship position and orientation. The LOS Guidance system receives the information of actual path η and desired path ηd, and formulates the referenced yaw angle ψref for next step. The sliding-mode controller functions through the controlling of yaw moment τr. The last unit is ship dynamic system, and it outputs the path η in real time. By transmitting information which is mentioned above, the closed-loop control system is set up.

Fig. 1 Framework of closed-loop control system
3.1 High-gain observer design
In the feedback control of path following, the velocities and yaw rate are needed. In the case of only the ship position and yaw angle information available, designing a proper observer to estimate the velocities is required. Whether the high-gain observer works mainly relying on the choice of the gains, it is important to properly design the gains [21]. By combining the high- gain observer theory with the concrete form of system (1, 2) and taking the parametric uncertainty into account, a nonlinear observer is constructed as follows:

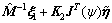 (7)
(7)
where 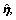

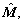
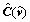 and
and 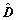 denote the estimated values of corresponding variables, respectively; the error variables are further defined as
denote the estimated values of corresponding variables, respectively; the error variables are further defined as

 (8)
(8)
K1=diag(k11, k12, k13) and K2=diag(k21, k22, k23) are the filter gains which need to be chosen, whose functions are to make the observer GES. The GES is obtained by defining a Lyapunov function candidate:
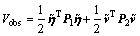 (9)
(9)
where P1=diag(p11, p12, p13) and P2=diag(p21, p22, p23) are both positive definite matrices. Differentiating both sides of Eq. (9) along Eq. (7) yields
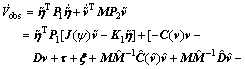
 (10)
(10)
Noticing that  thus
thus

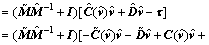
 (11)
(11)
where

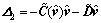 (12)
(12)
Inserting Eq. (11) to Eq. (10) yields

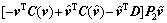 (13)
(13)
By defining p11=p12 and P1=K2MP2, then we have
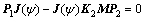 (14)
(14)
Defining p21=p22=p23, that is P2=p21I, thus from 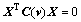 , yields
, yields
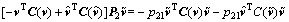
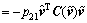 (15)
(15)
Substituting Eqs. (14) and (15) into Eq. (13) yields
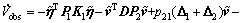
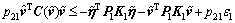 (16)
(16)
where 
Defining
 (17)
(17)
Thus Q1 and Q2 are both positive definite. Defining  and
and
 (18)
(18)
Then, we have the following formulas:

 (19)
(19)
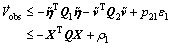
 (20)
(20)
where 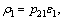 λmin and λmax denote the minimum and maximum eigenvalues, respectively. Hence
λmin and λmax denote the minimum and maximum eigenvalues, respectively. Hence
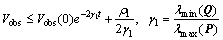 (21)
(21)
which further yields
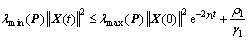 (22)
(22)
The Eq. (22) directly shows that
 (23)
(23)
where 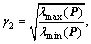

Thus,  is GES and it will converge into a compact set in finite time and then keep in it.
is GES and it will converge into a compact set in finite time and then keep in it.
Remark 1: It is important to note that, by properly choosing the parameters P1, P2, K1, K2, which means increasing λmin(Q) and decreasing λmax(P), γ2 can be made arbitrarily small, similarly the observation errors  and
and 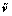 .
.
3.2 LOS guidance law design
In conventional line-of-sight guidance, some waypoints are preset to form a set of broken lines. By controlling the ship’s orientation to force the ship track along the broken lines, the aim of path following can be achieved [22]. In this work, the LOS guidance law is improved to make it be applied to track curved lines. The LOS method is chosen not just for its simple form, but also its high applicability in path following, especially for underactuated ship.
Defining the error variable vector
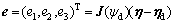 (24)
(24)
where 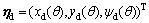 is the desired path, and θ is the desired path parameter. xd (θ) and yd (θ) are twice differentiable about θ, and ψd is defined as follows according to Ref. [23]:
is the desired path, and θ is the desired path parameter. xd (θ) and yd (θ) are twice differentiable about θ, and ψd is defined as follows according to Ref. [23]:
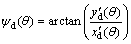 (25)
(25)
The Cartesian transformation of e can be seen from Fig. 2.
For convenience of writing, the following symbols are defined:
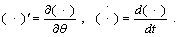

Fig. 2 Sketch of problem and Cartesian coordination transformation
Differentiating both sides of Eq. (24) yields
 (26)
(26)
where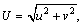
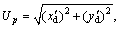 ψR=e3=ψ- ψd.
ψR=e3=ψ- ψd.
The LOS guidance law and update law of θ are designed as
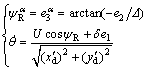 (27)
(27)
where △>0 is the look-ahead distance, and △>0 is a designed parameter.
Defining the referenced yaw angle as
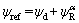 (28)
(28)
Thus, the yaw angle error has the following relationships:
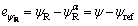 (29)
(29)
To avoid the differentiating of ψref, a third-order filter is introduced.
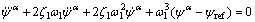 (30)
(30)
where ζ1>0 is the damping coefficient; ω1>0 is the inherent frequency; and  is the filtered referenced yaw angle.
is the filtered referenced yaw angle.
3.3 Sliding-mode controller design
Firstly, we define the yaw angle error and first-order sliding surface as follows:
 (31)
(31)
 (32)
(32)
where λ1>0, λ2>0 are both designed parameters.
From Eq. (32), that we have
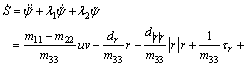
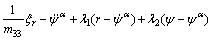 (33)
(33)
The control input τr is originally designed as
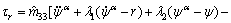
 (34)
(34)
where τ is a control parameter; 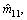
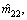
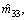
 and
and 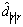 are the estimated values of m11, m22, m33, dr and d|r|r respectively, and they are all positive. Then, the parameter estimation errors are defined as
are the estimated values of m11, m22, m33, dr and d|r|r respectively, and they are all positive. Then, the parameter estimation errors are defined as 
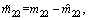

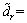

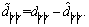
Assumption 3: The parameter estimation errors are bounded, and meet the following condition.

To show that S is bounded, the following Lyapunov function is defined:
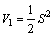 (35)
(35)
Whose derivative along the solution of Eq. (33) satisfies

 (36)
(36)
Then, we design the control parameter τ as
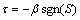 (37)
(37)
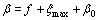 (38)
(38)

 (39)
(39)
where β0>0 is a small positive, and sgn(S) is the switching function, which is defined as
 (40)
(40)
Substituting Eqs. (38) and (40) into Eq. (37) yields
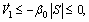
Hence, the sliding surface S is asymptotic stable, and it will reach S=0 in finite time and then maintain this state. Thus it can make  asymptotic stable, i.e.
asymptotic stable, i.e. 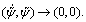
However, the switching function sgn(S) is discontinuous as defined, thus discontinuity is brought into the feedback control. High frequency dynamics may be aroused by the control input chattering, and eventually affect the performance and robustness of controller. An alternative way to overcome the possible chattering is using a continuous function instead of sgn(S). Therefore, we introduce the saturation function sat(S) [24] and it is defined as
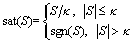 (41)
(41)
where κ is the boundary layer thickness.
As the real velocities are unknown, we combine the proposed observer and sliding-mode algorithm together, and modify the yaw angle error as
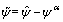 (42)
(42)
From Eqs. (34), (37), (41) and (42), we get the final form of yaw moment input τr:

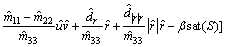 (43)
(43)
Substituting Eq. (43) into Eqs. (33) and (36) yields

 (44)
(44)
Where 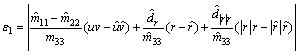
As the high-gain observer is proved to be convergent, we have sufficient reasons to assume that the velocities’ estimation is accurate enough; thus ε1 will be a small positive.
According to the relation between |S| and κ, we divide the problem two situations and discuss separately.
Situation A: 
Then, Eq. (44) transforms to
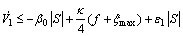 (45)
(45)
If we choose  thus
thus
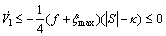 (46)
(46)
Situation B: 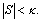
Then, Eq. (44) transforms to

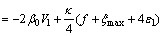 (47)
(47)
Thus
 (48)
(48)
Under the effect of feedback control law, the sliding surface will reach the region  in finite time; Once it reaches and then keeps in this region. By choosing a small κ, and increasing β0 appropriately, we can minimize the sliding surface stabilization error.
in finite time; Once it reaches and then keeps in this region. By choosing a small κ, and increasing β0 appropriately, we can minimize the sliding surface stabilization error.
3.4 Stability analysis
Defining the following Lyapunov function:
 (49)
(49)
where k>0 is a constant. Differentiating Eq. (49) and substituting Eq. (28) into it yields
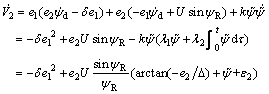
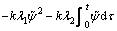 (50)
(50)
where 
By choosing small k and λ2, we have
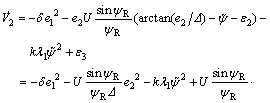
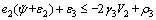 (51)
(51)
 (52)
(52)
where 


Since ρ3 is an arbitrary small positive, the system (e1, e2, 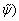 will converge to a small neighborhood about zero in finite time by increasing γ3. The ship will complete the convergence of initial position errors rapidly, and sail along the pre-defined path.
will converge to a small neighborhood about zero in finite time by increasing γ3. The ship will complete the convergence of initial position errors rapidly, and sail along the pre-defined path.
4 Numerical simulation
To illustrate the effectiveness of the proposed control law, the real parameters of a monohull ship are used in the simulation. The ship is equipped with one propeller and one rudder and has the length of 38 m and total mass of 118×103 kg; The motion parameters are provided by Ref. [6], m11=120×103 kg, du=215×102 kg·s-1, d|u|u=0.2du, m22=177.9×103 kg, dv=147×103 kg·s-1, d|v|v=0.2dv, m33=636×105 kg, dr=802×104 kg·s-1, d|r|r=0.2dr.
In the simulation, ρ is assumed to be 0.15, that is to say the parameter perturbation of ship model is less than 15%. So considering an extreme situation, we choose the estimates nominal motion parameters as follows:

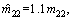
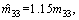

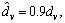




The initial states of the ship are picked as [x(0), y(0), ψ(0), u(0), v(0), r(0), θ(0)]=[-330 m, 20 m, π/4, 10 m/s, 0, 0, -π]. And the initial values of observer are set as 

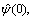

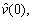
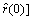 =[-320 m, 30 m, π/4, 9 m/s, 0, 0]. The observer gain matrixes are chosen as K1=diag{0.1, 0.1, 0.2}, K2=diag{0.01, 0.01, 0.5}. Other parameters presented in the controller designation are chosen as β=0.5, △=20, △=0.2, ζ1=1.5, ω1=10, k=1×10-6, κ=0.5, λ1=0.12, λ2=0. The surge thrust is chosen as
=[-320 m, 30 m, π/4, 9 m/s, 0, 0]. The observer gain matrixes are chosen as K1=diag{0.1, 0.1, 0.2}, K2=diag{0.01, 0.01, 0.5}. Other parameters presented in the controller designation are chosen as β=0.5, △=20, △=0.2, ζ1=1.5, ω1=10, k=1×10-6, κ=0.5, λ1=0.12, λ2=0. The surge thrust is chosen as 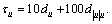 Considering the maximum rudder angle limitation, the yaw moment input is bounded. So, we assume that |τr|max=3×103 kN·m.
Considering the maximum rudder angle limitation, the yaw moment input is bounded. So, we assume that |τr|max=3×103 kN·m.
The desired path is designed as a curved line, composed by three components as follows.

To simulate the wave disturbance at State 4 sea condition, we use the model discussed in Ref. [25]. Thus, the environmental disturbance is ξ=h(s)M[wu(s), wv(s),wr(s)]T, where h(s)=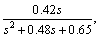 and wu(s), wv(s),wr(s) are all zero mean Gaussian white noise, with power spectral density of 0.01, 0.005, 0.1 respectively. In the simulation, the maximum values of ξu/m11, ξv/m22, and ξr/m33 reach 0.1 m/s2, 0.04 m/s2 and 0.5°/s2 respectively, which is accordant with the practical situation.
and wu(s), wv(s),wr(s) are all zero mean Gaussian white noise, with power spectral density of 0.01, 0.005, 0.1 respectively. In the simulation, the maximum values of ξu/m11, ξv/m22, and ξr/m33 reach 0.1 m/s2, 0.04 m/s2 and 0.5°/s2 respectively, which is accordant with the practical situation.
Figure 3 plots the actual sailing path and desired path. The ship sails off the desired path at x=600 m due to the unsmooth desired path. In Fig. 3, we can see that the ship tracks along the desired path well under the effect of sliding-mode controller, though with the influences of wave disturbance and motion parameters uncertainty.

Fig. 3 Sailing path of ship
Figure 4 shows the actual ship velocities and corresponding estimated values. As we can see from the figure, the estimated values approximate the real values accurately. So, we can judge that the proposed observer has a good observation effect under the combined influence of wave disturb and uncertain parameters. In addition, the observer works as a filter in Fig. 4(a) and it has a positive effect in decreasing the output oscillation.
The position observation errors are shown in Fig. 5, though the errors can’t converge to zero because of the inaccurate motion parameters, but they can be kept in an acceptable small region. In Fig. 6, the yaw angle observation error oscillates around the zero point under the affection of wave disturb, but the absolute value will be less than 0.5° after being converged, and the accuracy is enough for practical applications.

Fig. 4 Time-plot of ship velocities and estimated value:
Figures 7 and 8 plot the error curves of ship position (e1, e2) and yaw angle (ψR) respectively. It is easy to find that the initial errors are rapidly eliminated. For the time-varying output of yaw moment shown in Fig. 9, the chattering did not occur. The small-amplitude oscillation around equilibrium point is due to the non-vanishing wave disturbance. The simulation shows that the designed observer and controller are correct and effective, and the total control system is with good robustness.

Fig. 5 Observation errors of ship position:

Fig. 6 Observation error of yaw angle

Fig. 7 Error condition of ship’s position

Fig. 8 Error condition of yaw angle

Fig. 9 Response of yaw moment output
5 Conclusions
1) An improved method is proposed to steer an underactuated ship sailing along a given path, and the method is with robustness to parametric uncertainty and environmental disturbances.
2) The high-gain observer specified to the nonlinear ship dynamics is proposed and the real-time estimation of ship velocities has been well achieved, and the main advantage of this observer is that it doesn’t need motion parameters to be accurate.
3) The sliding-mode controller built on LOS guidance law is designed, which can accomplish the rapid stabilization of position and yaw angle error under underactuated condition. The sliding surface can neutralize the influence of wave disturb, and has a good performance in dealing with the parametric uncertainty problem, thus make the control system robust.
4) The nonlinear output feedback control law is proved to be SGES by using Lyapunov method, and simulation results demonstrate the effectiveness and robustness of the proposed approach.
References
[1] DO K D, JIANG Z P, PAN J. Universal controllers of stabilization and tracking of underactuated ships [J]. Systems & Control Letters, 2002, 47(4): 299-317.
[2] SANTHAKUMAR M, ASOKAN T. Investigations on the hybrid tracking control of an underactuated autonomous underwater robot [J]. Advanced Robotics, 2010, 24(11): 1529-1556.
[3] DO K D. Formation control of underactuated ships with elliptical shape approximation and limited communication ranges [J]. Automatica, 2012, 48(5): 1380-1388.
[4] GHOMMAM J, MNIF F, BENALI A, DERBEL N. Nonsingular Serret–Frenet based path following control for an underactuated surface vessel [J]. Journal of Dynamic Systems, Measurement, and Control, 2009, 131(2): 021006.
[5] YANG Ying, XIA Guo-qing, ZHAO Wei-guang. Path following in 3D for underactuated autonomous underwater vehicle based on ocean-current observer [J]. Control Theory & Applications, 2013, 30(8): 974-980. (in Chinese)
[6] DO K D, JIANG Z P, PAN J. Robust adaptive path following of underactuated ships [J]. Automatica, 2004, 40(6): 929-944.
[7] DING Lei, GUO Ge. Formation control for ship fleet based on backstepping [J]. Control and Decision, 2012, 27(2): 299-303. (in Chinese)
[8] PERERA L P, GUEDES SOARES C. Pre-filtered sliding mode control for nonlinear ship steering associated with disturbances [J]. Ocean Engineering, 2012, 51(6): 49-62.
[9] SONG Li-zhong, LI Huai-shu, YANG Zhi-hong, ZHOU Gang. Discrete-time sliding mode predictive control algorithm and its application [J]. Control and Decision, 2006, 21(7): 829-832. (in Chinese)
[10] NGO Q H, HONG K S. Sliding-mode antisway control of an offshore container crane [J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(2): 201-209.
[11] FANG M C, LUO J H. On the track keeping and roll reduction of the ship in random waves using different sliding mode controllers [J]. Ocean Engineering, 2007, 34(3): 479-488.
[12] LIU Yu, GUO Chen, L Jin. Sliding-mode control of ship course tracking based backstepping [J]. Journal of Central South University: Science and Technology, 2007, 38(Suppl.1): 278-282. (in Chinese)
Jin. Sliding-mode control of ship course tracking based backstepping [J]. Journal of Central South University: Science and Technology, 2007, 38(Suppl.1): 278-282. (in Chinese)
[13] OH S R, SUN J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control [J]. Ocean Engineering, 2010, 37(2): 289-295.
[14] GE S S, ZHANG J. Neural-network control of nonaffine nonlinear system with zero dynamics by state and output feedback [J]. IEEE Transactions on Neural Networks, 2003, 14(4): 900-918.
[15] CHEN M, GE S S. Robust adaptive position mooring control for marine vessels [J]. IEEE Transactions on Control System Technology, 2013, 21(2): 395-408.
[16] FOSSEN T I,  . Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping [J]. IEEE Transactions on Control System Technology, 1998, 6(1): 121-128.
. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping [J]. IEEE Transactions on Control System Technology, 1998, 6(1): 121-128.
[17] DU Jia-lu, YANG Yang, GUO Chen, LI Guang-qiang. Output feedback control for dynamic positioning system of a ship based on a high gain observer [J]. Control Theory & Applications, 2013, 30(11): 1486-1491. (in Chinese)
[18] TEE K P, GE S S. Control of fully actuated ocean surface vessels using a class of feedforward approximators [J]. IEEE Transactions on Control System Technology, 2006, 14(4): 750-756.
[19] DO K D. Practical control of underactuated ships [J]. Ocean Engineering, 2010, 37(13): 1111-1119.
[20] LIAO Yu-lei, ZHANG Ming-jun, WAN Lei. Serret-Frenet frame based on path following control for underactuated unmanned surface vehicles with dynamic uncertainties [J]. Journal of Central South University, 2015, 22(1): 214-223.
[21] GE S S, ZHANG J. Neural-network control of nonaffine nonlinear system with zero dynamics by state and output feedback [J]. IEEE Transactions on Neural Networks, 2003, 14(4): 900-918.
[22] FOSSEN T I. Handbook of marine craft hydrodynamics and motion control [M]. Trondheim: John Wiley & Sons, 2011.
[23] GHOMMAM J, MEHRJERDI H, SAAD M, MANI F. Formation path following control of unicycle-type mobile robots [J]. Robotics and Autonomous Systems, 2010, 58(5): 727-736.
[24] WANG Yan. Research on nonlinear robust control of underactuated surface vessels motion [D]. Harbin: Harbin Engineering University, 2013: 56-70. (in Chinese)
[25] QIN Zi-he, LIN Zhuang, LI Ping, LI Xiao-wen. Sliding-mode control of underactuated ship based on LOS guidance [J]. Journal of Central South University: Science and Technology, 2016, 47(10): 3605-3611. (in Chinese)
(Edited by YANG Hua)
Foundation item: Projects(61004008, 51509055) supported by the National Natural Science Foundation of China; Project(61422230302162223013) supported by the Laboratory of Science and Technology on Water Jet Propulsion, China
Received date: 2015-07-02; Accepted date: 2015-12-17
Corresponding author: LIN Zhuang, Associate Research Fellow, PhD; Tel: +86-18845168688; E-mail: 18845168688@163.com