基于自适应滑模的智能小车路径跟踪控制
贾鹤鸣1,王嘉鹏2,郭婧3
(1. 哈尔滨工程大学 自动化学院,黑龙江 哈尔滨,150001;
2. 哈尔滨华德学院 计算机应用技术系,黑龙江 哈尔滨,150025;
3. 东北林业大学 机电工程学院,黑龙江 哈尔滨,150040)
摘要:针对智能小车的路径跟踪问题,提出一种自适应滑模控制方法。为实现系统对参数变化和外部扰动的鲁棒性,基于Lyapunov稳定性理论,通过自适应律在线调节控制增益参数,并且设计适当的边界层条件抑制滑模控制器的高频抖振。仿真实验的结果表明,设计的控制器可以实现智能小车对期望路径的精确跟踪。
关键词:智能小车;路径跟踪;自适应滑模控制
中图分类号:TP242.6 文献标志码:A 文章编号:1672-7207(2011)S1-0432-04
Adaptive sliding mode for path following control of an intelligent vehicle
JIA He-ming1, WANG Jia-peng2, GUO Jing3
(1. College of Automation, Harbin Engineering University, Harbin 150001, China;
2. Department of Computer Applied Technology, Harbin Huade University, Harbin 150025, China;
3. College of Mechanical and Electrical Engineering, Northeast Forest University, Harbin 150040, China)
Abstract: An adaptive sliding mode controller was proposed for path following problem of an intelligent vehicle. In order to achieve system robustness against parameter variations and external disturbances, based on Lyapunov stability theorem, suitable control gain parameters were systematically on-line computed based on adaptive law. The boundary layer condition was adopted to reduce the high frequency chattering in the switching part of the sliding mode controller. Simulation results illustrate that satisfactory trajectory tracking performance is achieved effectively.
Key words: intelligent vehicle; path following; adaptive sliding mode control
随着社会和科学的发展,许多研究者对无人智能小车路径跟踪控制问题进行了研究并取得了一些成 果[1-4],在工程应用中要求无人小车具有精确的循迹跟踪能力,这就对控制器的设计提出了更高的要求。传统的PID控制器由于其设计的简单性和使用的有效性而被广泛地应用于无人智能小车。PID控制器的3个增益参数,比例增益、积分增益和微分增益通常是固定的,其缺点是处理系统不确定性的能力差,如系统模型参数的变化和外部干扰。一般来说,在实际工况下系统模型参数测量不精确、环境干扰难测定问题普遍存在。滑模控制(SMC)是处理不确定控制系统非常实用的控制策略之一[5-6],SMC的主要特点是具有对系统参数变化和外部扰动的强鲁棒性,已在机械手、直流电机等领域有广泛的应用[7-9]。为了保证系统的鲁棒性以抑制系统模型的参数变化和外部干扰的影响,本文作者提出了基于SMC的无人智能小车路径跟踪问题的自适应PID控制方法,基于Lyapunov稳定性理论分析了整个系统的稳定性,并采用边界层设计方法来抑制控制器的高频抖振[10]。
1 问题描述
1.1 智能小车的硬件实现
本文研究的智能小车长×宽×高为39.4 cm×20.8 cm×8.7 cm(见图1),车的质量为1.1 kg。图中,白色的跑道是由KT板制成,所需循迹的期望路径是1根20 kHz/100 mA的交流通电导线。在车辆前端的八线圈电感传感器能够检测到导体的磁场变化, 接收到信号将其转换成电信号进行解调,滤波和放大。然后将这些信号传输到A / D转换的主控制器MC9S12XS128MAA。在路径跟踪位移误差计算程序分析的基础上,车辆中心和导体之间的位移偏差很容易在线计算得到。利用PWM信号来控制舵机,驱动小车的前轮转动指定的角度。与此同时,为实现对车辆的速度控制,PWM是采用BTS7960驱动的H桥来控制直流电动机的转速。在路径跟踪的过程中,车辆的实时速度由光电编码盘收集并存储,收集的数据传送到所设计的控制器来快速的调节并达到期望的 速度。
图2所示为小车的系统模块框图。

图1 无人智能小车
Fig.1 Intelligent vehicle
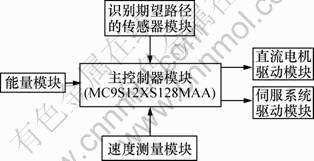
图2 系统模块框图
Fig.2 System block diagram
1.2 无人智能小车的模型
假设小车的横向速度为0 m/s,无人小车的模型可以为表示为如下形式:
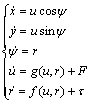 (1)
(1)
式中:x和y为小车的相对位移;ψ为偏航角;u为在小车的前向速度;r为偏航角速度;F为前向驱动力;τ为转向控制力矩;g(u,r)和f(u,r)分别为摩擦力和作用于小车的其他外力。为了获得更简化的模型以便于控制器的设计,定义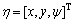 ,
,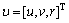 ,则式(1)可以写为:
,则式(1)可以写为:
 (2)
(2)
显然系统(2)的相对阶为2,选择坐标转换
 (3)
(3)
则系统(2)可以表示为:
 (4)
(4)
其中,ξ1和ξ2是可测状态;u是控制输入;Y为输出;b为控制增益;f(ξ1,ξ2)是模型的标称参量;Δf(ξ1,ξ2)是模型的不确定量;d表示外界干扰。假设存在2个正的上界g和α,且满足|Δf(·)|≤g和|d|≤α。定义e为期望轨迹和实际输出Y之间的误差,并且满足e=Yd-Y。
2 智能小车路径跟踪的自适应滑模控制器设计
为得到二阶误差动态系统,定义如下信号:
 (5)
(5)
其中:k1和k0是待设计参数,满足s2+k1s+k0=0的根在左半复平面上。在一般情况下,可以选择k1=2ζωn和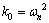 ;ζ为阻尼比;ωn为固有频率。
;ζ为阻尼比;ωn为固有频率。
本节中提出的自适应滑模控制器设计过程将分为2个步骤。
第1步 定义一个滑模面函数;
第2步 设计控制律令该系统到达并保持在期望滑模面σ=0上。
首先,定义滑模面函数即
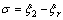 (6)
(6)
若滑模面存在,令σ=0,则
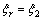 (7)
(7)
将式(7)代入式(5)得:
 (8)
(8)
这意味着随着时间的增长(t→∞),跟踪误差最终将趋于0(e→0)。
令控制输入u满足
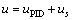 (9)
(9)
其中,
 (10)
(10)
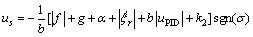 (11)
(11)
增益k2是一个正的标量参数,sgn(σ)是符号函数,即
 (12)
(12)
PID控制器的3个增益kP,kI和kD可以利用下面的自适应率在线计算,其中ηi>0定义为学习率,i=1,2,3。
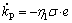 (13)
(13)
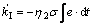 (14)
(14)
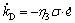 (15)
(15)
为了证明系统的稳定性,选择Lyapunov函数为
 (16)
(16)
对式(16)求导可得:
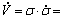
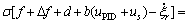

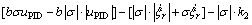 (17)
(17)
进一步得
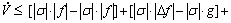
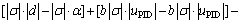
 (18)
(18)
因此,控制律由式(9)~(12)给出,自适应律式(13)~(15)可以确保系统达到并保持在滑模面上。
一般情况下,控制输入固有的高频抖振会限制设计的控制方法的实际应用性,本文采用饱和函数代替式(11)中的符号函数sgn(σ)来抑制抖振问题,
 (19)
(19)
其中,δ是边界层的宽度,给定任意的初始值设计的滑模面函数σ都将到达并保持在边界层|σ|≤δ中。
3 仿真分析
图3所示为智能小车的路径跟踪的实验示意图。

图3 无人小车的路径跟踪控制
Fig.3 Path following control of intelligent vehicle
为了进一步验证所提出的控制器的有效性,在MATLAB软件环境下进行仿真并与传统的PID控制算法进行比较,所选择的参数如下:期望循迹路径为1.5+sin(0.1t),小车的初始速度为u=0。此外,选择阻尼比ζ=1,固有频率ωn=6,使s2+k1s+k0=0的根k1=12和k0=36在左半复平面的开区间上。PID控制器的增益kP,kI和kD初始值为0。学习率ηi设定为2,i=1,2,3。边界层设置为δ=0.1。根据设计的控制律(10)和(11),无人智能小车路径跟踪控制曲线如图4和5 所示。
从图4和图5可以清楚地看出:输出Y能够快速的收敛到所需的路径Yd,即本文所提出的自适应滑模控制器比传统的PID控制方法在路径跟踪的精确性上更有效,更优越。
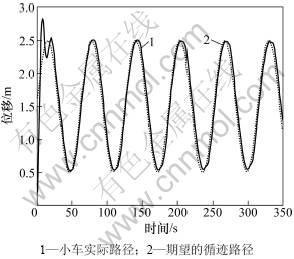
图4 自适应滑模控制路径跟踪
Fig.4 Adaptive sliding mode path following control
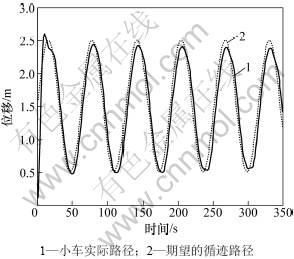
图5 PID控制路径跟踪
Fig.5 PID path following control
4 结论
(1) 针对无人智能小车的路径跟踪问题,基于Lyapunov稳定性理论设计了一个具有PID增益自适应调节功能的滑模控制器。控制器的设计无需针对系统的线性化模型且不需要进行先验学习,它可以在线实时应用。
(2) 设计的控制器具有满意的循迹跟踪效果,可以满足实际工程的应用需求。
参考文献:
[1] GUO Li, CAO Cheng-kao, HE Jan-biao, et al. Robust PD control of unmanned land vehicles [C]//Proceedings of Computer, Communication, Control and Power Engineering. Beijing: IEEE, 1993: 186-189.
[2] 王建, 张晓炜, 杨锦. 基于视觉传感器的自主循迹智能车的设计与实现[J]. 工业仪表与自动化装置, 2010(6): 34-44.
WANG Jian, ZHANG Xiao-wei, YANG Jin. Design and implementation of a self-tracking smart car based on visual sensor[J]. Industrial instrument and Automation, 2010(6): 34-44.
[3] Djapic V, Farrell J, Land vehicle control using a command filtered backstepping approach[C]//American Control Conference. USA:IEEE, 2008: 2461-2466.
[4] Jafri S, Shakeel S Z. Improved path planning and controlling for a low cost navigation solution of unmanned land vehicle[C]//2009 11th International Conference on Computer Modelling and Simulation. Pliscataway: IEEE, 2009: 14-18.
[5] Zinober A. Variable structure and lyapnuov control[M]. Berlin: Springer-Verlag, 1994: 26-32.
[6] Young K D, Utkin V I, Ozguner U. A control engineer’s guide to sliding mode control[J]. IEEE Transactions on Control System Technology, 1999, 7(3): 328-342.
[7] Choi H S, Park Y H, Cho Y S, et al. Global sliding-mode control improved design for a brushless DC motor[J]. IEEE Control Systems Magazine, 2001, 21(3): 27-35.
[8] Huang Y J, Kuo T C, Robust control for nonlinear time-varying systems with application to a robotic manipulator[J]. Intern J Syst, 2002, 33(2): 831-837.
[9] Huang Y J, Kuo T C. Robust position control of DC servomechanism with output measurement noise[J]. Electr Eng, 2006, 88(1): 223-238.
[10] Slotine J J, Li W, Applied nonlinear control[M]. New Jersy: Prentice-Hall, 1991: 112-124.
(编辑 赵俊)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:教育部新世纪优秀人才支持计划项目(2009)
通信作者:贾鹤鸣(1983-),男,黑龙江哈尔滨人,博士研究生,从事非线性系统控制设计研究;电话:13206666920;Email:jiaheminglucky99@126.com