基于Bishop条分法的边坡可靠度应用研究
彭振斌，李俊，彭文祥
(中南大学 地学与环境工程学院，湖南 长沙 410083)
摘 要：基于Bishop条分法，研究隐式功能函数边坡工程稳定可靠度计算方法。将传统的响应面分析方法与Bishopt条分法相结合，形成一种新的边坡稳定可靠性响应面分析方法。采用此方法分析某一边坡工程的稳定可靠性，并把分析结果与蒙特卡洛模拟法计算结果进行对照。研究结果表明：该方法计算效率较高，原理简单，精度满足 要求。
关键词：边坡可靠度；Bishop条分法；隐式功能函数；响应面法
中图分类号：TU413.6 文献标志码：A 文章编号：1672-7207(2010)02-0668-05
Application analysis of slope reliability based on
Bishop analytical method
PENG Zhen-bin, LI Jun, PENG Wen-xiang
(School of Geosciences and Environmental Engineering, Central South University, Changsha 410083, China)
Abstract: Based on Bishop slice method, a calculation method of reliability for slope stability whose state function was implicit function was studied. Combining classical response surface method with Bishop slice method, a new response surface method of slope stability reliability analysis was established. The new method was applied to analyze the stability of slope and the procedure and calculation result were compared with those obtained by MonteCarlo method. The results show that the calculation efficiency of the proposed method is high and the accuracy of calculation result is acceptable.
Key words: slope reliability; Bishop slice method; implicit performance function; response surface method
边坡稳定性问题是岩土工程中的基本研究问题之一。目前, 在工程设计中常用的稳定分析方法为定值分析法。定值设计法是经过长期工程实践证明的一种有效设计方法，但是, 这种方法最大的缺点是没有考虑实际存在的不确定性(包括荷载效应以及抗力等不确定性)的影响。由于边坡工程岩土力学参数及破坏模式的随机性和复杂性，可靠度理论是建立在土体具有的抗力大于荷载的概率基础上进行设计和校核的，因此，采用该法进行边坡稳定性分析更符合客观实际。何满潮等[1]采用块体理论，建立了块状结构岩体工程稳定可靠性模型；黄志全等[2]基于块体理论和模糊分析理论，提出边坡块状结构岩体模糊随机可靠性分析点估计法，并对某边坡块体可靠性进行计算，与模糊概率测度分析方法进行对比；杨坤等[3]用支持向量机来估计边坡工程的可靠性；罗文强等[4]从工程安全系数与可靠性指标出发，建立边坡安全系数与可靠性相耦合的二元评价体系。但这些研究主要是针对特定的边坡岩体结构类型及对新理论进行应用。响应面方法(Response surface method，RSM)是统计学的综合试验技术，用于处理复杂系统的输入(基本变量)和输出(系统响应)之间的转换关系。其基本思想是用响应面函数(Response surface fitting, RSF)来拟合原有的隐式极限状态函数，具有既能利用确定性有限元方法进行分析，又能减少数值模拟次数的优点。Wong[5]利用响应面法与有限元相结合分析边坡的稳定性；张弥等[6]引进有限元响应面法分析了铁路明洞的荷载效应；苏永华 等[7]采用响应面法与数值模拟相结合分析了地下岩体空间的可靠性，取得了较好的结果。有理多项式具有很强的计算功能，Chowdhury等[8]采用有理多项式技术计算了边坡稳定的可靠度；徐军等[9]采用有理多项式解决了岩土工程中功能函数具有高次非线性和复杂性的求导问题。但Chowdhury等[8]在均值点处计算功能函数对基本变量的偏导，其可靠指标结果接近于中心点法的结果。由于响应面的形式一般为二次多项式，这很可能会遇到极限响应面存在2条分支、用验算点法求可靠指标时验算点会收敛到错误分支的情况。谭晓慧等[10]提出一种改进的响应面法，在整个计算过程中只需拟合1个响应面，从而大大地减少了计算工作量及收敛到错误分支的可能性。在大多数情况下，边坡成熟力学模式下的可靠度分析体现为隐式极限状态方程的可靠度计算。目前，主要采用Monte-Carlo有限元法，计算工作量大，尤其对非线性问题计算量更大，妨碍其在工程中应用推广。为此，本文作者将边坡定值性分析方法与可靠性分析方法结合起来，基于简化Bishop法建立边坡极限状态函数，针对安全系数用隐函数表示这一特点，提出用响应面法求解极限状态函数关于基本变量的偏导数, 用JC法求解边坡的可靠性指标及失效概率，进行边坡的可靠度安全评价。
1 功能函数的建立
1955年，毕肖普(Bishop)在瑞典法基础上提出了Bishop法[11]。这一方法保留了滑裂面的形状为圆弧形和通过力矩平衡条件求解的特点，但是，在确定土条底部法向力时，考虑了条间力的作用[11]，在求解边坡稳定性时，需满足以下前提：
(1) 假定滑动面圆弧滑裂面，将滑动土体分为N条竖向土条，并假定每个土条为不变形的刚体；
(2) 假定土条竖直侧向力X=0，或侧向力与水平向的夹角β=0?，即土条两侧作用力均沿水平方向。
这时，作用于1条条块的力化简为图1(a)所示的情况。任意条块处于平衡状态时，其力矢多边形应闭合，如图1(b)所示。
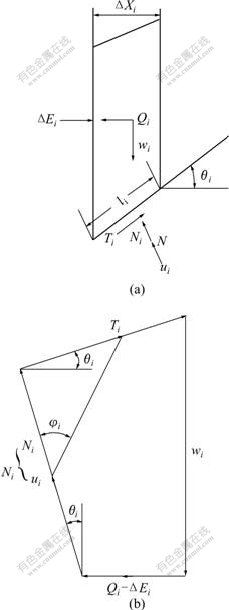
(a) 条块的力简化图；
(b) 任意条块处于平衡状态时的力矢多边形
图1 Bishop法受力图
Fig.1 Force diagram of Bishop method
为了维持闭合条件，条块与滑床之间的抗剪力应满足以下关系式：
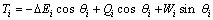(1)
式中：
(2)
在Bishop法中，假设各条块有相同的安全系数。
将式(2)代入式(1)，并对全部条块求和。这时，由于Ei是条块间的力，故
，从而得到：
(3)
式中：Fs为稳定安全系数；θi为第i条块底边与水平线夹角(?)；Wi为第i条块的重力(kN)；Ni为第i条块的总正压力(kN)；
为第i条块的有效正压力(kN)；Qi为第i条块的地震力(kN)；ui为第i条块的孔隙水压力(kN)；Ti为第i条块的剪切阻力(kN)；?Ei为第i条块两侧法向力之差(kN)；?Xi为第i条块两侧切向力之差(kN)；ri为第i条块土的重度(kN/m3)；hi为第i条块中心点垂直高度(m)；li为第i条块滑面的长度(m)；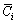
为第i条块有效应力下内黏聚力(kPa)；
为第i条块有效应力下内摩擦角(?)；rw为水容重(kN/m3)；hwi为第i条块中心点水头高度(m)。
在边坡可靠性分析中，为了建立功能函数，采用的一般原则是将定值分析中计算安全系数Fs公式的右侧之分子和分母相减，即定义：
z=g(x)=R(x)-S(x) (4)
其中：R(x)/S(x)=Fs。这种方法只对简单的土坡稳定分析模型(如Fellenious模型)才适用；对于其他分析模型(如简化的Bishop模型)，Fs是用迭代法求解的，即Fs(x)=R(x, Fs)/S(x)。为了适应上述原则，一般令Fs=1。
由上述分析可建立如下极限状态方程：
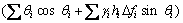(5)
2 可靠度分析的JC法
JC法是“国际结构安全度联合委员会”(JCSS)推荐的一种方法。结构的可靠度通常受各种荷载、材料性能、几何尺寸、计算公式精确性等因素的影响，这些因素一般具有随机性，称为“基本变量”，记为xi (i=1, 2, …, n)。按极限状态方法设计结构时，针对所要求的各种性能(如强度、刚度、抗裂度等)，通常可以建立包括有关基本变量在内的关系式为：
Z=g(x1, x2, …, xn)=0 (6)
这一关系式称为“极限状态方程”。其中Z=g(?)称为结构的“功能函数”。
当功能函数与多个正态基本变量有关时，式(8)代表以基本变量xi (i=1, 2, …, n)为坐标的n维欧氏空间上的1个曲面。将功能函数在验算点P*展开泰勒级数，并仅保留其1次项，经推导可知：可靠指标β是标准正态空间坐标系中原点到极限状态曲面的最短距离，可用以下方程组迭代求解：
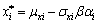(7)
(8)
(9)
式中：i=1, 2, …, n；
表示计算偏导时变量均在P*点赋值。利用式(7)~(9)可得到可靠指标β及验算点坐标值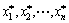
。
当基本变量xi为非正态随机变量时，则需进行当量正态化处理。当有相关性的随机变量时，可首先采用正交变换，转换为相互独立的随机变量，然后求解。求出β后，就可以利用关系式
求出相应的失效概率[12-13]。
3 响应面方法计算偏导数
3.1 响应面方法
响应面方法(RSM)由有限元数值模拟、定值抽样规则及结构可靠度极限状态方程拟合3部分组成，其基本思想是：通过设计一系列变量值, 每一组变量值组成1个试验点，然后，逐点进行结构有限元数值计算得到对应的功能函数值。通过这些变量组和功能函数值拟合1个明确表达的函数关系，以此函数为基础计算可靠概率或失效概率。设结构有n个随机变量x1, x2, …, xn，兼顾简单性和灵活性，对于拟合函数的表达形式，通常取不含交叉项的二次多项式形式[14-15]：
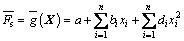(10)
式中：a，bi和di (i=1, 2, …, n)为待定系数，共2n+1个待定系数。
RSM方法运算过程按下述步骤进行。
步骤1：假定迭代点
，初次计算时一般取平均值点。
步骤2：利用试验(在本文中采用Bishop法)得出功能函数
和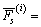
, 得到2n+1个点的函数值，其中：系数f在第1轮估计中取3，在以后的迭代计算中取1；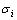
为xi的均方差。
步骤3：由于式(10)有2n+1个待定系数，利用步骤2求得2n+1个函数值，解出待定系数a，bi和ci (i=1, 2, …, n)，确定二次多项式近似功能函数。
步骤4：利用JC法求解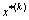
和可靠度指标
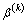和其中：上标k表示第k步迭代。
步骤5：判断收敛条件
＜
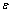(11)
是否满足(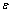为预先设定的误差限)，若不满足, 则用插值法得到新的展开点：
(12)
此插值可使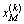
较接近极限状态曲面, 然后返回步骤2进行下一步迭代，直至收敛条件满足。
3.2 基于Bishop条分法的边坡极限状态方程RSM 重构
从式(5)可以看出：安全系数是一个隐函数。根据RSM方法，取安全系数的近似显式形式为式(10)。将影响边坡稳定性随机参数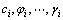
表达为随机向量X=(x1, x2, …, xn)，则安全系数Fs的近似显式表达式为
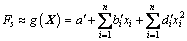(13)
式中：
，
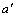和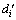
(i=1, 2, …, n)均为待定系数，共2n+1个待定系数。边坡稳定盈余系数近似方程为
(14)
边坡稳定的极限状态重构方程为
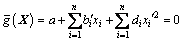(15)
在确定功能函数的近似解析表达通式后，将RSM的重构思路与Bishop法的迭代方法结合起来确定式(14)中的待定系数[16-18]。具体步骤为：按照以上方法重构步骤1，第1次抽出各随机变量的均值，代入Bishop的迭代方法中得1个安全系数，即可以看作1次边坡稳定性试验结果。然后，按照RSM方法步骤2~4，抽得2n组参数试样，代入Bishop法中，共得出2n+1个安全系数。将安全系数代入式(14)，解相应的方程组即可得出式(14)中的待定系数，这样就确立边坡稳定状态方程。然后，按照RSM方法步骤4算出可靠度指标β，按照步骤5形成新的展开点；按照收敛条件，进行循环迭代计算。
4 算例分析与评价
已知某公路边坡高度H=6 m，坡角θ=55?，土容重γ=18.6 kN/m3，土内摩擦角
=12?，黏聚力c=16.7 kPa，内摩擦角和粘聚力的标准差分别为：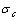
=2 kPa，
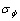=15?。将c和分别采用正态分布、对数正态分布，就这2种情况计算边坡的可靠度。
蒙特-卡罗模拟法(简称MCSM)是求解可靠性问题比较精确的方法[13]，其基本原理是：当已知基本变量X呈概率分布时，可利用适当的随机数发生器，产生符合状态变量X概率分布的一组随机数(x1, x2, …, xn)，代入状态函数g(X1, X2, …, Xn)计算状态函数的1个随机数g(x1, x2, …, xn)，并看它是否小于0。以同样式方法产生M个状态函数的随机数据。若M个状态函数的随机数中有m个小于0，则当M足够大时，由大数定律可知系统的失效概率Pf为：Pf=P(g(x1, x2, …, xn)＜0)=m/M。为了与其他方法的计算结果进行比较, 取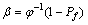
，以验证其精确度。
通过自编程序采用蒙特-卡罗模拟法模拟计算该边坡的可靠指标和可靠度，当模拟次数达到2万次时，计算结果见表1。可见：当模拟次数达2万次时，可靠度趋于稳定。
表1 模拟次数为2万次时的可靠度计算结果
Table 1 Reliability calculation results when simulation times is 20 000
5 结论
(1) 以Bishop法为例，提出利用边坡稳定性力学分析模式作为试验计算手段，结合RSM重构其近似极限状态方程。
(2) 利用RSM重构建立的近似极限状态方程计算边坡可靠度，计算效率较高，为隐式功能函数可靠度的分析提供了一种近似分析方法。
(3) 工程实例分析及比较结果表明，基于Bishop条分法的边坡稳定可靠性响应面分析方法计算精度满足工程要求。
参考文献：
[1] 何满潮, 苏永华, 景海河. 块状岩体的稳定可靠性分析模型及其应用[J]. 岩石力学与工程学报, 2002, 21(3): 343-348.
HE Man-chao, SU Yong-hua, JING Hai-he. Reliability analysis model of blocky rockmass stability and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3): 343-348.
[2] 黄志全, 李华晔, 马莎, 等. 岩石边坡块状结构岩体稳定性分析和可靠性评价[J]. 岩石力学与工程学报, 2004, 23(24): 4200-4205.
HUANG Zhi-quan, LI Hua-ye, MA Sha, et al. Stability analysis and reliability evaluation of slope of block construction for rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(24): 4200-4205.
[3] 杨坤, 周创兵, 张昕, 等. 边坡块状结构岩体模糊随机可靠性分析[J]. 岩石力学与工程学报, 2006, 25(2): 407-413.
YANG Kun, ZHOU Chuang-bing, ZHANG Xin, et al. Fuzzy-random reliability analysis of blocky rock mass in slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(2): 407-413.
[4] 罗文强, 王亮清, 龚珏. 正态分布下边坡稳定性二元指标体系研究[J]. 岩石力学与工程学报, 2005, 24(13): 2288-2292.
LUO Wen-qiang, WANG Liang-qing, GONG Jue. Study on slope stability by dual index system based on normal distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2288-2292.
[5] Wong F S. Slope reliability and response surface method[J]. Journal of Geotechnical Engineering, 1985, 111(1): 32-53.
[6] 张弥, 沈永清. 用响应面方法分析铁路明洞结构荷载效应[J]. 土木工程学报, 1993, 26(2): 58-65.
ZHANG Mi, SHEN Yong-qing. Analysis of loading effect on railway cut-and-cover tunnel structure by numerical response surface method[J]. China Civil Engineering Journal, 1993, 26(2): 58-65.
[7] 苏永华, 方祖烈, 高谦. 用响应面方法分析特殊地下岩体空间的可靠性[J]. 岩石力学与工程学报, 2000, 19(1): 55-58.
SU Yong-hua, FANG Zu-lie, GAO Qian. Reliability analysis on special underground rockmass space by response surface method[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(1): 55-58.
[8] Chowdhury R N, Xu D W. Rational polynomialtechnique in slope-reliability analysis[J]. Journal of Geotechnical Engineering, 1993, 119(12): 1910-1928.
[9] 徐军, 刘东升, 郑颖人. 具有高次非线性和复杂性功能函数的岩土工程可靠度分析[J]. 岩石力学与工程学报, 2001, 20(2): 160-163.
XU Jun, LIU Dong-sheng, ZHENG Ying-ren. Reliability analysis for the high order nonlinearity and complexity of the performance function in geotechnical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(2): 160-163.
[10] 谭晓慧, 王建国, 刘新荣. 改进的响应面法及其在可靠度分析中的应用[J]. 岩石力学与工程学报, 2005, 24(S2): 5874-5879.
TAN Xiao-hui, WANG Jian-guo, LIU Xin-rong. Improved response surface method and its application to reliability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S2): 5874-5879.
[11] Biship A W. The use of the slip circle in the stability analysis of earth slopes[J]. Geotechnique, 1955, 5(1): 7-17.
[12] 赵国藩. 工程结构可靠性理论及其应用[M]. 大连: 大连理工大学出版社, 1996.
ZHAO Guo-fan. Reliability theory of engineering structural and its application[M]. Dalian: Dalian University of Technology Press, 1996.
[13] 祝玉学. 边坡可靠性分析[M]. 北京: 冶金工业出版社, 1993.
ZHU Yu-xue. Slope reliability analysis[M]. Beijing: China Metallurgical Industry Press, 1993.
[14] 徐军, 邵军, 郑颖人. 遗传算法在岩土工程可靠度分析中的应用[J]. 岩土工程学报, 2000, 22(5): 586-589.
XU Jun, SHAO Jun, ZHENG Ying-ren. Application of genetic algorithm to reliability analysis of geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(5): 586-589.
[15] 徐军, 郑颖人. 响应面重构的若干方法研究及其在可靠度分析中的应用[J]. 计算力学学报, 2002, 19(2): 217-222.
XU Jun, ZHENG Ying-ren. Research on response surface structure method and its application to reliability analysis[J]. Chinese Journal of Computational Mechanics, 2002, 19(2): 217-222.
[16] 苏永华, 赵明华, 邹志鹏, 等. 边坡稳定性分析的Sarma模式及其可靠度计算方法[J]. 水利学报, 2006, 37(4): 457-463.
SU Yong-hua, ZHAO Ming-hua, ZOU Zhi-peng, et al. Sarma model for slope stability analysis and its reliability degree calculation method[J]. Journal of Hydraulic Engineering, 2006, 37(4): 457-463.
[17] 苏永华, 赵明华, 蒋德松, 等. 响应面方法在边坡稳定可靠度分析中的应用[J]. 岩石力学与工程学报, 2006, 25(7): 1417-1424.
SU Yong-hua, ZHAO Ming-hua, JIANG De-song, et al. Application of response surface method to stability reliability analysis for slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1417-1424.
[18] 苏永华, 赵明华, 李青海, 等. 稳定性系数为隐式函数的边坡可靠度近似计算方法[J]. 岩土工程学报, 2006, 28(10): 1198-1203.
SU Yong-hua, ZHAO Ming-hua, LI Qing-hai, et al. Approximative method to calculate reliability of slope with stability coefficient to be implicit expression[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1198-1203.
收稿日期：2009-08-15；修回日期：2009-10-21
基金项目：国家自然科学基金资助项目(50878212)
通信作者：李俊(1980-)，男，湖北麻城人，博士研究生，从事岩土工程、边坡工程的研究；电话：13616883301；E-mail: spidermanlijun@163.com
(编辑 陈灿华)
