DOI: 10.11817/j.issn.1672-7207.2017.08.018
鸡群算法的收敛性分析
吴定会,孔飞,纪志成
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡,214122)
摘 要:
立Markov链数学分析模型,分析此Markov链的一些性质,证明鸡群状态序列是有限齐次Markov链。结合随机算法收敛准则,证明鸡群算法能够满足随机算法全局收敛的2个准则,保证算法全局收敛。将算法应用于15个标准测试函数寻优问题,并同标准粒子群算法、蝙蝠算法进行比较。实验结果表明:该算法具有较好的全局收敛性和计算鲁棒性,尤其适合高维、多峰的复杂函数求解。
关键词:
鸡群算法;Markov链;状态转移;全局收敛;标准测试函数;
中图分类号:TP301.6 文献标志码:A 文章编号:1672-7207(2017)08-2105-08
Convergence analysis of chicken swarm optimization algorithm
WU Dinghui, KONG Fei, JI Zhicheng
(Key Laboratory of Advanced Process Control for Light Industry,
Ministry of Education, Jiangnan University, Wuxi 214122, China)
Abstract: The Markov chain model for chicken swarm optimization (CSO) was established, and the properties of the model were analyzed, which proved that chicken swarm state sequence was a finite homogeneous Markov chain. According to the convergence criteria of stochastic search algorithm, chicken swarm optimization was demonstrated to meet the two convergence criteria, so that the global convergence was ensured. Finally, 15 benchmark functions were used to test the CSO algorithm, and the comparison with particle swarm optimization (PSO) and bat algorithm (BA) was also performed. The simulation results show that CSO outperforms other algorithms in terms of global convergence and computational robustness, and it is particularly suitable for solving high-dimension and multimodal function optimization problems.
Key words: chicken swarm optimization; Markov chain; state transition; global convergence; benchmark functions
群体智能优化算法(简称SIA)是通过模拟自然界生物的群体行为而构造的随机优化算法[1],如遗传算法[2-3]、粒子群算法(简称PSO)[4-6]、蚁群算法(简称ACO)[6-7]、人工蜂群算法(简称ABC)[8-12]、人工鱼群算法(简称AFSA)[13]、狼群算法(简称WPA)[14]、蝙蝠算法(简称BA)[15]等。这些算法为解决大量存在于计算科学、工程科学、管理科学等科研领域的全局优化问题提供了新的求解途径,因此,成为科研人员长期研究的热点。但这些算法的理论依据多来源于对生物群落社会性的模拟,缺乏相关的理论性分析,算法中参数设置无确切的理论依据,都是依据经验确定的,所以,对群体智能优化算法的理论性研究显得尤为重要。鸡群算法(简称CSO)是由MENG等[16]提出的一种基于鸡群搜索行为的群体智能优化算法,它模拟了鸡群等级制度和鸡群行为。整个鸡群分为若干子群,每一个子群都由1只公鸡、若干只母鸡和小鸡组成。不同鸡遵循不同的移动规律,在具体的等级制度下,子群之间存在竞争行为,它是一种全局优化算法。目前,已经有学者提出了改进算法,并将其用于求解约束优化问题。但是,鸡群算法由于小鸡粒子容易陷入局部最优而无法取得全局最优解[17],关于鸡群算法的收敛性分析,国内外几乎没有文献报道,因此,对鸡群算法进行收敛性分析具有很重要的理论价值。Markov链理论在随机算法收敛性分析以及收敛概率分析上具有较强的能力,它是一类占有重要地位、具有普遍意义的随机过程,其应用相当广泛,目前已经应用于模拟退火、粒子群算法、蚁群算法和人工蜂群算法等随机算法的收敛性分析[18-21]。本文作者采用Markov链理论对鸡群算法的收敛性进行分析,通过建立鸡群算法的Markov链模型,研究鸡群状态的转移行为,结合随机算法的收敛准则分析算法的收敛性能。通过仿真实验验证鸡群算法的寻优性能。
1 鸡群优化算法
鸡群算法是由MENG等提出的一种基于鸡群搜索行为的随机优化方法,它模拟了鸡群等级制度和鸡群行为。在描述算法前,先进行如下假设:
1) 设整个鸡群A中存在着若干子群,A1,A2,…,An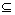 A;每个子群An都由1只公鸡、若干只母鸡和小鸡组成,分别用An1,An2,An3表示,其中An1,An2,An3
A;每个子群An都由1只公鸡、若干只母鸡和小鸡组成,分别用An1,An2,An3表示,其中An1,An2,An3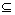 An。
An。
2) 如何把鸡群分成若干子群、如何确定鸡的种类取决于鸡自身的适应度。鸡群中,适应度最高的若干个体作为公鸡,并且每只公鸡都是1个子群的头目,具有最低适应度的若干个体作为小鸡,剩余的个体就作为母鸡。母鸡随便选择属于哪个子群,母鸡和小鸡的母子关系也是随机建立的,其母子关系映射为f(x)。
3) 鸡群等级制度、支配关系和母子关系一旦建立了就保持不变,直至数代以后才开始更新。
4) 每个子群中的个体都围绕这个子群中的公鸡寻找食物,也可以阻止其他个体抢夺自己的食物;并且假设小鸡可以随机偷食其他个体已经发现的食物,每只小鸡跟随他们的母亲一起寻找食物。鸡群中具有支配地位的个体具有良好的竞争优势。
在解决优化问题时,鸡群中的每个个体都对应优化问题的1个解。假设NR,NH,NC和NM分别为公鸡、母鸡、小鸡和妈妈母鸡的个数。在整个鸡群中,所有的个体数假设为N,每个个体的位置xi,j(t)表示第i个体的j维在第t次迭代值。
整个鸡群有3种类型的鸡,鸡群中个体位置更新公式随着鸡种类的不同而不同。公鸡对应鸡群A中适应度值最好的个体,它们可以在更广泛的空间寻找食物,公鸡对应的位置更新公式如下:
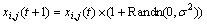 (1)
(1)
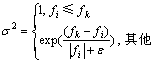
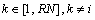 (2)
(2)
式中: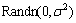 表示均值为0,标准差为
表示均值为0,标准差为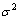 的一个高斯分布;ε为1个很小的常数,防止发生零除错误;k为所有公鸡中除去i后的任一个体;f为与x对应的适应值。母鸡的位置更新公式如下:
的一个高斯分布;ε为1个很小的常数,防止发生零除错误;k为所有公鸡中除去i后的任一个体;f为与x对应的适应值。母鸡的位置更新公式如下:
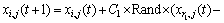
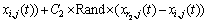 (3)
(3)
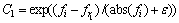 (4)
(4)
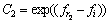 (5)
(5)
式中:Rand为[0,1]之间均匀分布的随机数;r1为第i只母鸡所在子群Ai中的公鸡,即r1∈Ai1;r2为整个鸡群A中公鸡和母鸡中随机选取的任意元素,即r2∈(A11∪A21∪…∪An1∪A12∪A22∪…An2)。小鸡的位置更新公式如下:
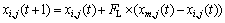 (6)
(6)
式中:m为第i只小鸡对应的母鸡,即m∈M,M为母鸡m所在子群中的所有母鸡,其中M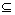 (A12∪A22∪…∪An2)且m=f(xi);FL(FL[0,2])为跟随系数,表示小鸡跟随母鸡寻找食物。
(A12∪A22∪…∪An2)且m=f(xi);FL(FL[0,2])为跟随系数,表示小鸡跟随母鸡寻找食物。
2 鸡群算法的Markov链模型
为了证明方便,不考虑粒子的维数,对鸡群中个体位置更新公式进行如下简化。
公鸡的位置更新公式为
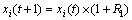 (7)
(7)
式中:R1取[0,1]之间的固定值。
母鸡的位置更新公式为
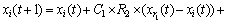
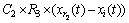 (8)
(8)
式中:R2和R3取[0,1]之间的随机数,但是对于确定的个体,R2和R3是确定的;C2<1<C1。
小鸡的位置更新公式为
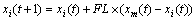 (9)
(9)
为了说明鸡群算法的Markov链模型,首先给出一些相关定义和数学描述[22-23]。
定义1(鸡的状态和鸡的状态空间)鸡的状态由鸡群中鸡的位置构成,记为x。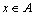 ,A为可行解空间。鸡的所有可能状态构成鸡的状态空间,记为
,A为可行解空间。鸡的所有可能状态构成鸡的状态空间,记为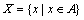 。
。
定义2(鸡群状态和鸡群状态空间)鸡群中所有鸡的状态构成鸡群状态,记为s=(x1,x2,…,xN)(式中,xi为第i只鸡的状态,N为鸡群中个体的总数)。鸡群中所有状态组成的集合构成鸡群状态空间,记为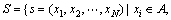
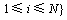 。
。
定义3(状态等价)对于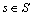 ,
,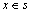 ,记
,记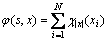 。其中
。其中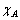 为事件A的示性函数,
为事件A的示性函数,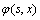 为鸡群状态s中包含鸡的状态x的数目。设有2个鸡群状态
为鸡群状态s中包含鸡的状态x的数目。设有2个鸡群状态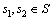 ,对于
,对于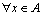 ,若有
,若有 ,则称s1和s2等价,记作s1~s2。
,则称s1和s2等价,记作s1~s2。
定义4(状态等价类)由等价关系“~”在S上诱导的鸡群状态等价类记作L=S/~,简称鸡群等价类。
鸡群等价类存在以下性质:
1) 某等价类L内任意鸡群状态都是等价的,即si~sj,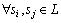 。
。
2) L内任意鸡群状态和L外任意鸡群状态不等价。
3) 任意2个不同等价类没有交集,即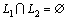 ,
,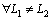 。
。
定义5(鸡的状态转移)对于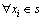 ,
,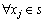 ,鸡群算法迭代中,鸡的状态xi一步转移到xj,记作Ts(xi)=xj。
,鸡群算法迭代中,鸡的状态xi一步转移到xj,记作Ts(xi)=xj。
定理1 鸡群算法中,鸡的状态xi一步转移到xj的转移概率为
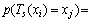
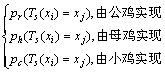 (10)
(10)
证明:因为鸡群中3种鸡的位置更新公式不同,所以,3种鸡对应的一步转移概率也不相同。鸡的群体为超空间的一组点集,则鸡群中个体位置更新过程是在超空间中进行点集之间的变换。由定义5和鸡群算法的几何性质,可得公鸡由状态xi一步转移到xj的转移概率为
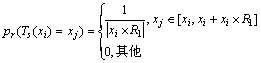 (11)
(11)
母鸡由状态xi一步转移到xj的转移概率为
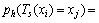
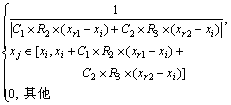 (12)
(12)
小鸡由状态xi一步转移到xj的转移概率为
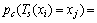
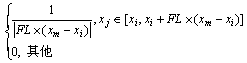 (13)
(13)
证毕。
定义6(鸡群的状态转移概率)对于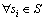 ,
, ,鸡群算法迭代中,鸡群状态si一步转移到sj,记作
,鸡群算法迭代中,鸡群状态si一步转移到sj,记作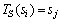 。鸡群状态由si一步转移到sj的转移概率为
。鸡群状态由si一步转移到sj的转移概率为
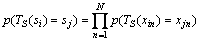 (14)
(14)
式中:N为鸡群中个体数。即鸡群算法中鸡群状态si一步转移到sj的概率为鸡群内所有鸡的状态同时转移到鸡群sj内所有鸡的状态。
定义7(鸡群等价类之间的转移概率)假设由等价关系“~”在S上引起的任意2个鸡群状态等价类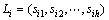 ,
,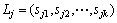 ,则Li一步转移到Lj,记为
,则Li一步转移到Lj,记为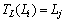 ,其一步转移概率为
,其一步转移概率为
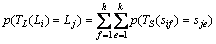 (15)
(15)
表明鸡群等价类之间的转移包括等价类Li中的所有鸡群转移到等价类Lj中的所有鸡群。
3 鸡群优化算法的收敛性分析
定义8(Markov链):设有随机过程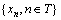 ,参数集T为离散的时间序列,即T={0,1,2,…},对应可能取值xn的全体组成离散的状态空间I={i0,i1,i2,…}。若对于任意的整数
,参数集T为离散的时间序列,即T={0,1,2,…},对应可能取值xn的全体组成离散的状态空间I={i0,i1,i2,…}。若对于任意的整数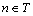 和任意
和任意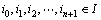 满足以下条件概率
满足以下条件概率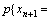
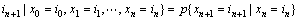 ,则称
,则称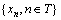 为Markov链。
为Markov链。
定义9(有限Markov链)若状态空间I是有限的,则称该Markov链是有限Markov链。
定义10(齐次Markov链)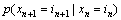 表示系统在n时刻所处的状态in经过转移达到新状态in+1的条件概率,若该概率仅与n时刻的状态有关,而与时刻n无关,则称该Markov链为齐次Markov链。
表示系统在n时刻所处的状态in经过转移达到新状态in+1的条件概率,若该概率仅与n时刻的状态有关,而与时刻n无关,则称该Markov链为齐次Markov链。
定理2 CSO所产生的种群序列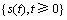 是有限齐次Markov链,其中t为迭代次数。
是有限齐次Markov链,其中t为迭代次数。
证明:首先证明鸡群序列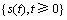 是Markov过程,然后证明该Markov链满足齐次性和有限性。由定义6知:鸡群状态序列
是Markov过程,然后证明该Markov链满足齐次性和有限性。由定义6知:鸡群状态序列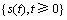 中,
中,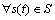 ,
,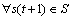 ,其转移概率
,其转移概率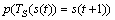 由鸡群内所有鸡的转移概率
由鸡群内所有鸡的转移概率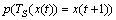 决定。由定理1可知:鸡群内任意鸡的状态转移概率
决定。由定理1可知:鸡群内任意鸡的状态转移概率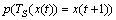 仅与t时刻的状态x(t)以及[0,1]之间的随机数R1,R2和R3,[0,2]之间的随机数FL,C1和C2,母鸡对应的公鸡xr1,整个鸡群中公鸡和母鸡中随机选取的任意个体xr2和小鸡对应的妈妈母鸡xm相关。所以,
仅与t时刻的状态x(t)以及[0,1]之间的随机数R1,R2和R3,[0,2]之间的随机数FL,C1和C2,母鸡对应的公鸡xr1,整个鸡群中公鸡和母鸡中随机选取的任意个体xr2和小鸡对应的妈妈母鸡xm相关。所以,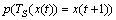 也仅与t时刻的状态相关,而与t时刻无关,由定义8可知,CSO所产生的种群序列
也仅与t时刻的状态相关,而与t时刻无关,由定义8可知,CSO所产生的种群序列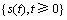 具有Markov性。又因为鸡群状态空间S是有限的,根据定义9可知,CSO所产生的种群序列
具有Markov性。又因为鸡群状态空间S是有限的,根据定义9可知,CSO所产生的种群序列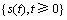 构成1个有限的Markov链。再由定理1可知:
构成1个有限的Markov链。再由定理1可知: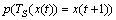 也仅与t时刻的状态相关,而与t时刻无关,因此,CSO所产生的种群序列
也仅与t时刻的状态相关,而与t时刻无关,因此,CSO所产生的种群序列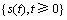 是有限齐次Markov链。证毕。
是有限齐次Markov链。证毕。
3.1 收敛准则
鸡群优化算法属于随机搜索算法,因此本文通过随机算法收敛准则判定鸡群算法的收敛行为[24]。
对于优化问题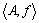 ,有随机优化算法D,第k次迭代的结果为xk,则下一次迭代的结果为
,有随机优化算法D,第k次迭代的结果为xk,则下一次迭代的结果为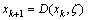 。其中:A为可行解空间,f为适应度函数;
。其中:A为可行解空间,f为适应度函数; 为算法D迭代搜索中曾经搜索到的解。
为算法D迭代搜索中曾经搜索到的解。
定义搜索的下确界:
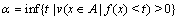 (16)
(16)
式中:v(x)表示在集合x上的勒贝格测度,定义最优解区域:
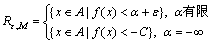 (17)
(17)
式中: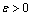 ;C为充分大的正数。如果随机算法D找到
;C为充分大的正数。如果随机算法D找到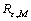 中的1个点,则可认为算法找到了可接受的全局最优或近似全局最优点。
中的1个点,则可认为算法找到了可接受的全局最优或近似全局最优点。
条件H1 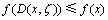 ,且若
,且若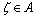 ,则有
,则有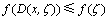 。
。
条件H2 对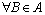 ,
, ,有
,有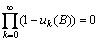 其中uk(B)为算法D第k次迭代搜索解在集合B上的概率测度。
其中uk(B)为算法D第k次迭代搜索解在集合B上的概率测度。
定理3(随机算法全局收敛)设f是可测的,可测空间A是Rn上可测度的子集,算法D满足条件H1和条件H2,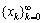 是算法D产生的序列,则有:概率测度
是算法D产生的序列,则有:概率测度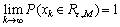 ,
,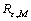 为最优区域,即算法D全局收敛。
为最优区域,即算法D全局收敛。
3.2 鸡群算法的收敛性
定理4 CSO算法满足条件H1。
证明:CSO算法每次迭代时都要更新个体当前最优位置,即
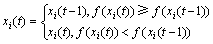 (18)
(18)
故CSO算法每次迭代都保存了群体最佳位置,满足条件H1。证毕。
定义11(鸡群最优状态集G)设优化问题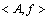 的最优解是g*,定义鸡群的最优状态集
的最优解是g*,定义鸡群的最优状态集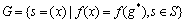 。
。
若G=S,则在可行解空间中每个解不仅是可行解而且是最优解,此时进行优化是无意义的,下面的讨论都是基于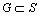 的。
的。
定义12(吸收态Markov链)基于鸡群算法种群序列的Markov链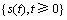 和最优状态集
和最优状态集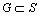 ,若
,若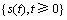 满足条件概率
满足条件概率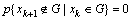 ,则称该Markov链为吸收态的Markov链。
,则称该Markov链为吸收态的Markov链。
定理5 鸡群算法所产生的Markov链是吸收态Markov链。
证明:在鸡群算法优化中,个体的更新采取最优个体的保留机制,即只有当前最优个体的适应度值好于原个体适应度时,原先最优个体才会被替换,如式(18)所示。从而保证了算法在每次迭代进化过程中,使得新产生的个体不差于之前产生的个体,所以条件概率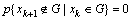 满足,即鸡群算法产生的种群序列
满足,即鸡群算法产生的种群序列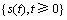 是吸收态的Markov链。证毕。
是吸收态的Markov链。证毕。
定理6 鸡群算法中,最优鸡群状态集G是状态空间S上的1个闭集。
证明: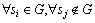 ,
,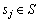 ,有
,有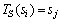 的转移概率为
的转移概率为
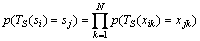 ,
,
在G中至少有1个粒子的状态达到了最优,设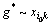 为最优状态,即至少
为最优状态,即至少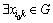 ,那么,至少存在
,那么,至少存在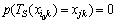 ,此时,
,此时,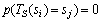 ,所以,最优鸡群状态集G是状态空间S上的1个闭集。证毕。
,所以,最优鸡群状态集G是状态空间S上的1个闭集。证毕。
定理7 鸡群状态空间S中不存在非空闭集M,使得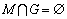 。
。
证明:采用反证法。假设状态空间S中还存在1个非空闭集M,且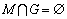 。设
。设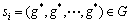 ,
,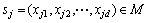 ,有
,有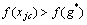 。由Chapman-Kolmogorov方程可得
。由Chapman-Kolmogorov方程可得
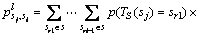
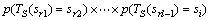 (19)
(19)
算法经过有限次迭代会满足定理1中的条件(11)~(13)。所以当步长l足够大时,式(19)中展开式的每一项中一步转移概率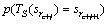 都满足定理1中的条件(10),即
都满足定理1中的条件(10),即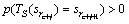 ,从而
,从而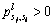 ,得出M不是闭集,与题设矛盾。因此,鸡群状态的Markov链是不可约的,状态空间S不含除G之外的闭集。
,得出M不是闭集,与题设矛盾。因此,鸡群状态的Markov链是不可约的,状态空间S不含除G之外的闭集。
根据文献[25],本文不加证明的给出定理8。
定理8 假定Markov链有一个非空闭集E,且不存在另一个非空闭集O,使得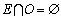 ,则当
,则当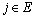 时,有
时,有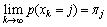 ,且当
,且当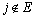 时,有
时,有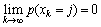 。
。
定理9 当鸡群内部迭代趋于无穷时,鸡群状态序列必将进入最优状态集G。
证明:由定理6、定理7和定理8即可得出定理9成立。证毕。
定理10 鸡群算法收敛到全局最优。
证明:由定理4可知鸡群算法满足条件H1,由定理9可知,鸡群算法连续无穷次搜索不到全局最优解的概率为零,则有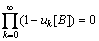 ,
,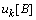 为鸡群算法第k次迭代搜索解在集合B上的概率测度。满足条件H2。鸡群算法在每次迭代时,个体的更新采取了最优个体的保留机制,即只有当前个体的适应度高于原先最优个体的适应度时,原先最优个体才会被替换,否则保留原最优个体。即当迭代趋于无穷时,
为鸡群算法第k次迭代搜索解在集合B上的概率测度。满足条件H2。鸡群算法在每次迭代时,个体的更新采取了最优个体的保留机制,即只有当前个体的适应度高于原先最优个体的适应度时,原先最优个体才会被替换,否则保留原最优个体。即当迭代趋于无穷时,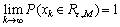 ,
,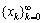 是鸡群算法迭代产生的序列。根据定理3可以得出鸡群算法是1个全局收敛算法。
是鸡群算法迭代产生的序列。根据定理3可以得出鸡群算法是1个全局收敛算法。
4 实验与分析
为了充分验证算法的性能与特点,需要引入较多具有不同特征的标准函数,本文采用文献[14]中的15个标准测试函数作为实验对象,这15个测试函数分为4类:单峰不可分函数、单峰可分函数、多峰不可分函数和多峰可分函数。
文献[14]中的这15个标准函数的变量维数从2维直至200维,都是难度较大的复杂优化问题,具有很好的测试性,可较为全面的反应各算法的性能。利用这15个测试函数对CSO算法、PSO和BA进行比较分析。
实验环境为:Windows7 系统,4G内存,CPU 3.4 GHz,算法基于Matlab R2011b用M语言实现。
为充分对比各算法的性能,利用CSO,PSO和BA 3种智能算法分别对15个复杂函数重复进行100次寻优计算,从最好值、最差值、平均值、标准差、平均耗时等多方面对算法进行评估。
实验设置的最大迭代次数为1 000,初始个体总数皆为100,3种算法所涉及的其他参数见表1。
表1 3种算法参数
Table 1 Parameter of three algorithms

表2给出了3种算法对15个复杂函数寻优计算的统计结果。其中,规定若计算结果小于1×10-20,则视为0。
最好值和平均值可体现算法的收敛精度和寻优能力。由表2可知:对于简单的低维函数如Easom,Matyas,Booth,Bohachevsky1,Eggcrate,Six Hump Camel Back,Bohachevsky3,PSO算法和CSO算法收敛精度相当高,基本都可以收敛到理论最优值。BA算法与PSO算法和CSO算法相比,收敛精度次之,所以,对于简单的低维函数,BA算法的寻优能力不如PSO算法和CSO算法。但随着变量维数的逐渐增加,算法的搜索空间复杂度呈指数倍增加。对于函数Trid6,Sumsquares和Sphere(维数分别为6,10和30),虽然这3种算法有不同程度的较强寻优能力,但是CSO算法对每一个测试函数都能收敛到理论最优值。当维数增加到60维(Rastrigin函数)、120维(Quadric函数)甚至200维(Ackley函数)时,虽然这3种算法都无法达到理论最优值,但是CSO算法收敛精度要明显高于PSO算法和BA算法收敛精度。特别对于Rastrigin函数,CSO算法的收敛值要比PSO算法和BA算法的收敛值小得多。由此可见CSO算法在处理多峰、高维复杂函数中具有很大的优势。
表2 函数优化结果对比
Table 2 Comparison of function optimization results
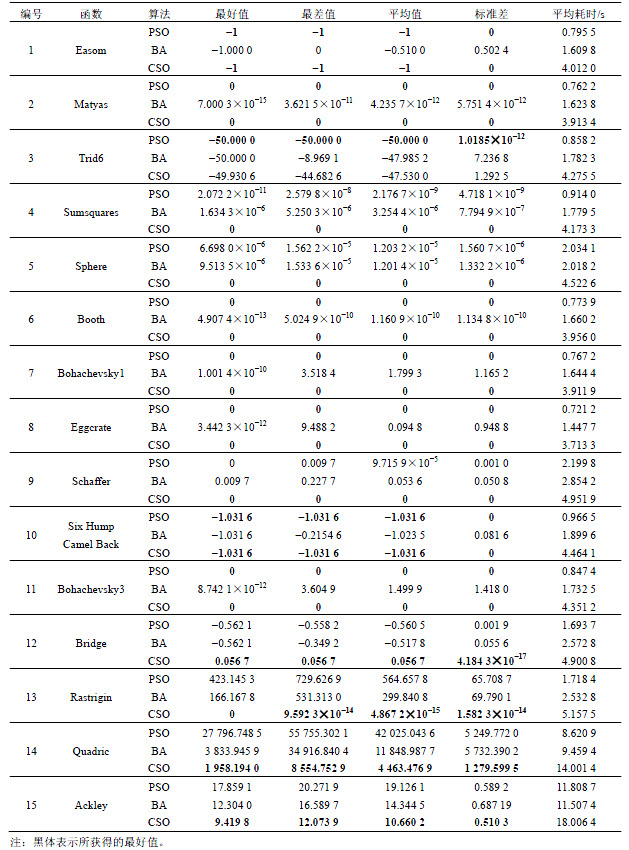
最差值和标准差体现了算法的鲁棒性和对抗局部极值的能力。由表2可知:除Bridge,Rastrigin,Quadric和Ackley外,PSO算法和BA算法对于其他低维函数的最差值接近理想值,标准差也较小,可见这2种算法对于低维函数的寻优计算具有一定的鲁棒性。但是与PSO算法和BA算法相比,CSO算法所获得的最差值始终更接近于理想最优值,标准差也始终最小,尤其对于测试函数Easom,Matyas,Booth,Bohachevsky1,Eggcrate,Schaffer,Six Hump Camel Back,Bohachevsky3,Sumsquares和Sphere,CSO算法所获得的最差值近似等于理论最优值,标准差近似为0。可见,CSO算法在函数寻优过程中具有良好的鲁棒性。
从平均耗时来看,对于所有的标准测试函数而言,PSO算法和BA算法的平均消耗时间相当,CSO算法的平均耗时要稍大于PSO算法和BA算法的平均耗时。但是对于计算时间要求不是特别高的优化问题,CSO算法因其具有较高的收敛精度和较强的鲁棒性而具有很明显的优势。
虽然CSO是一种全局收敛算法,对于大部分测试函数在规定的迭代次数内都能收敛到全局最优,但是对于表3中的函数Quadric和Ackley而言,在一定迭代次数内未能收敛到全局最优,这与算法的位置更新公式有关。具体地,算法中小鸡的位置更新公式中,小鸡只向自己的妈妈学习,并没有向小鸡所在子群中的公鸡学习,因而就无法获取整个子群中公鸡的位置信息,算法会陷入局部最优。为提高算法的收敛效率,需要对小鸡的位置更新公式进行改进。
5 结论
1) 在鸡群算法的基础上,描述了鸡的状态空间和鸡群状态空间,通过定义鸡群状态转移序列建立了Markov链数学分析模型,分析了该Markov链的性质,指出它是有限齐次Markov链,分析了鸡群状态序列最终转移状态,结合随机搜索算法的收敛准则,验证了鸡群算法的全局收敛性。
2) 通过鸡群算法与2种经典的智能算法在解决15个复杂函数寻优问题中的比较,实验结果显示鸡群算法对不同特征的复杂函数都具有较好的鲁棒性和全局收敛性能,可有效避免早熟收敛问题,可为大量非线性多峰值的工程问题求解提供新的思路和解决方法。下一步将对鸡群算法进行更深入的理论研究,如利用鞅序列理论对算法的收敛性进行进一步研究,设计改进鸡群算法并将其用于求解复杂的工程应用问题等。
参考文献:
[1] BEHESHTI Z, SHAMSUDDIN S M H. A review of population-based meta-heuristic algorithms[J]. International Journal of Advances in Soft Computing & Its Applications, 2013, 5(1): 1-35.
[2] PETEGHEM V V, VANHOUCKEAB M. A genetic algorithm for the preemptive and non-preemptive multi-mode resource- constrained project scheduling problem[J]. European Journal of Operational Research, 2010, 201(2): 409-418.
[3] 郑金华, 吕卉, 伍军, 等. 基于空间交配遗传算法的收敛 性分析[J]. 模式识别与人工智能, 2010, 23(2): 639-645.
ZHENG Jinhua, LV Hui, WU Jun, et al. Convergence analysis of genetic algorithm based on spaceMating[J]. PR&AI, 2010, 23(2): 639-645.
[4] KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE Press, 1995: 1942-1948.
[5] TAVAKKOLI MOGHADDAM R, AZARKISH M, SADEGHNEJAD BARKOUSARAIE A. A new hybrid multi-objective Pareto archive PSO algorithm for a bi-objective job shop scheduling problem[J]. Expert Systems with Applications, 2010, 38(9): 10812-10821.
[6] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems Man and Cybernetics (Part B): Cybernetics, 1996, 26(1): 29-41.
[7] SUN Bo, WANG Hui, FANG Yadong. Application of ant colony algorithm in discrete job shop scheduling[C]//Proceedings of the 2nd International Symposium on Knowledge Acquisition and Modeling (KAM). Wuhan, 2009: 29-31.
[8] XU Chunfan, DUAN Haibin. Artificial bee colony (ABC) optimized edge potential function (EPF) approach to target1558 recognition for low-altitude aircraft[J]. Pattern Recognition Letters, 2010, 31(13): 1759-1772.
[9] ZHU Guopu, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173.
[10] OMKAR S N, SENTHILNATH J, KHANDELWAL R, et al. Artificial bee colony (ABC) for multi-objective design optimization of composite structures[J]. Applied Soft Computing, 2011, 11(1): 489-499.
[11] KARABOGA D, OZTURK C. A novel clustering approach:artificial bee colony(ABC) algorithm[J]. Applied Soft Computing, 2011, 11(1): 652-657.
[12] HORNG M H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation[J]. Expert Systems with Applications, 2011, 38(11): 13785-13791.
[13] LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animats: Fish-swarm algorithm[J]. Systems Engineering Theory & Practice, 2002, 22(11): 32-38.
[14] 吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法—狼群算法[J]. 系统工程与电子技术, 2013, 35(11): 2430-2438.
WU Husheng, ZHANG Fengming, WU Lushan. New swarm intelligence algorithm-wolf pack algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2430-2438.
[15] YANG Xinshe. Bat algorithm: literature review and applications[J]. International Journal of Bio-Inspired Computation, 2013, 5(3): 141-149.
[16] MENG Xianbing, LIU Yu, GAO Xianzhi, et al. A new bio-inspired algorithm: chicken swarm optimization[C]//5th International Conference on Swarm Intelligence. Hefei: Springer International Publishing, 2014: 74-85.
[17] 孔飞, 吴定会. 一种改进的鸡群算法[J]. 江南大学学报(自然科学版), 2015, 14(6): 681-688.
KONG Fei, WU Dinghui. An improved chicken swarm optimization algrorithm[J]. Journal of Jiangnan University (Natural Science Edition), 2015, 14(6): 681-688.
[18] GIDAS B. Nonstationary Markov chains and convergence of the annealing algorithm[J]. Journal of Statistical Physics, 1985, 39(1/2): 73-131.
[19] 任子晖, 王坚, 高岳林. 马尔科夫链的粒子群优化算法全局收敛性分析[J]. 控制理论与应用, 2011, 28(4): 462-466.
REN Zihui, WANG Jian, GAO Yuelin. The global convergence analysis of particle swarm optimization algorithm based on Markov chain[J]. Control Theory & Applications, 2011, 28(4): 462-466.
[20] 苏兆品, 蒋建国, 梁昌勇, 等. 蚁群算法的几乎处处强收敛性分析[J]. 电子学报, 2009, 37(8): 1646-1650.
SU Zhaoping, JIANG Jianguo, LIANG Changyong, et al. An almost everywhere strong convergence proof for a class of ant colony algorithm[J]. Acta Electronica Sinica, 2009, 37(8): 1646-1650.
[21] 宁爱平, 张雪英. 人工蜂群算法的收敛性分析[J]. 控制与决策, 2013, 28(10): 1554-1558.
NING Aiping, ZHANG Xueying. Convergence analysis of artificial bee colony algorithm[J]. Control and Decision, 2013, 28(10): 1554-1558.
[22] 李宁. 粒子群优化算法的理论分析与应用研究[D]. 武汉: 华中科技大学控制科学与工程系, 2006: 42-70.
LI Ning. Analysis and application of particle swarm optimization[D]. Wuhan: Huazhong University of Science and Technology. Department of Automatic Control, 2006: 42-70.
[23] 钱伟民, 梁汉营, 杨国庆. 应用随机过程[M]. 北京: 高等教育出版社, 2014: 60-70.
QIAN Weimin, LIANG Hanying, YANG Guoqing. Applied stochastic processes[M]. Beijing: Higher Education Press, 2014: 60-70.
[24] SOLIS F J, WETS J B. Minimization by random search techniques[J]. Mathematics of Operations Research, 1981, 6(1): 19-30.
[25] 张文修, 梁怡. 遗传算法的数学基础[M]. 西安: 西安交通大学出版社, 2003: 67-87.
ZHANG Wenxiu, LIANG Yi. Mathematical foundation of genetic algorithm[M]. Xi’an: Xi’an Jiaotong University Press, 2003: 67-87.
(编辑 陈爱华)
收稿日期:2016-11-25;修回日期:2017-03-04
基金项目(Foundation item):国家自然科学基金资助项目(61572237,61573167);江苏省“六大人才高峰”项目(WLW-008)(Projects(61572237, 61573167) supported by the National Natural Science Foundation of China; Project (WLW-008) supported by Jiangsu Six Talents Peak-Funded Projects)
通信作者:吴定会,博士,副教授,从事风力发电、智能调度技术研究;E-mail:wdh123@jiangnan.edu.cn
摘要:针对鸡群算法建立Markov链数学分析模型,分析此Markov链的一些性质,证明鸡群状态序列是有限齐次Markov链。结合随机算法收敛准则,证明鸡群算法能够满足随机算法全局收敛的2个准则,保证算法全局收敛。将算法应用于15个标准测试函数寻优问题,并同标准粒子群算法、蝙蝠算法进行比较。实验结果表明:该算法具有较好的全局收敛性和计算鲁棒性,尤其适合高维、多峰的复杂函数求解。
[3] 郑金华, 吕卉, 伍军, 等. 基于空间交配遗传算法的收敛 性分析[J]. 模式识别与人工智能, 2010, 23(2): 639-645.
[14] 吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法—狼群算法[J]. 系统工程与电子技术, 2013, 35(11): 2430-2438.
[17] 孔飞, 吴定会. 一种改进的鸡群算法[J]. 江南大学学报(自然科学版), 2015, 14(6): 681-688.
[19] 任子晖, 王坚, 高岳林. 马尔科夫链的粒子群优化算法全局收敛性分析[J]. 控制理论与应用, 2011, 28(4): 462-466.
[20] 苏兆品, 蒋建国, 梁昌勇, 等. 蚁群算法的几乎处处强收敛性分析[J]. 电子学报, 2009, 37(8): 1646-1650.
[21] 宁爱平, 张雪英. 人工蜂群算法的收敛性分析[J]. 控制与决策, 2013, 28(10): 1554-1558.
[22] 李宁. 粒子群优化算法的理论分析与应用研究[D]. 武汉: 华中科技大学控制科学与工程系, 2006: 42-70.


