Trans. Nonferrous Met. Soc. China 24(2014) 2145-2149

Effect modeling of Cr and Zn on microstructure evolution during homogenization heat treatment of AA3xxx alloys

Qiang DU¹, Yan-jun LI²

1. SINTEF Materials and Chemistry, 7465 Trondheim, Norway;

2. Department of Materials Science and Engineering, NTNU, 7491 Trondheim, Norway

Received 17 October 2013; accepted 4 April 2014

Abstract: Both of chromium and zinc could appear as either minor impurities or alloying elements in recycled and commercial aluminum alloys, and they could have detrimental effects on the final product properties if not controlled in an appropriate way. A Kampmann-Wagner numerical modeling approach, built on the basis of computational thermodynamics and diffusion kinetics, is employed to investigate the effect of these two minor impurities on dispersoids precipitation during homogenization heat treatment of AA3xxx alloys. The simulation results obtained from different simulation set-ups were compared. The aim is to demonstrate that the modeling approach has the potential to guide the design or optimization of the chemical compositions and heat treatment parameters of aluminum alloys.

Key words: homogenization heat treatment; modeling; CALPHAD; diffusion; Kampmann-Wagner numerical model

1 Introduction

The recycling of aluminum alloys could reduce production cost and conserve the environment. Meanwhile, it complicates the control of chemical composition in the alloys due to the introduction of minor impurities such as chromium and zinc in the very beginning of the whole aluminum production chain. Although necessary procedures are taken in the aluminum melt treatment to remove some impurities, the subsequent casting and homogenization heat treatment processes are still exposed to minor but unpredictable variations in chemical compositions. This puts the existing casting and heat treatment parameters, which had been optimized for the melt by the traditional route (the aluminum from the primary production plus alloying elements additions), under stringent test. It is necessary to study the effect of those minor alloying element and impurity on solidification structure and heat treatment structure to enlarge processing window. To be concrete, for successful design of new alloys or optimization of heat treatment parameters, firstly one needs to address the formation of as-cast microstructure consisting of microsegregation and secondary phase particles. Secondly, the microstructural response of the initial as-cast microstructure to heat treatment, which includes the reduction in the extent of microsegregation, transformation and growth of secondary phase particles and precipitation of dispersoids should be addressed as demonstrated in Ref. [1]. Finally, the as-heat-treated microstructure interferences with deformation, recovery and recrystallization, which could be utilized in controlling the grain size, grain morphology and crystallographic texture in the final product [2]. As demonstrated by the other of the present authors, a comprehensive modeling approach, being validated by experimental measurements, is valuable in investigating the chemical composition effect [3]. AA3xxx alloys, an important commercial aluminum alloy containing manganese, iron and silicon, are chosen in our investigation. The alloys have been used in many industrial sectors due to their combination of moderate mechanical strength, high ductility and excellent corrosion resistance.

Thermodynamics is founded on the basis of heat treatment modeling. This is evidenced by the essential role of its graphical representation, phase diagram, in determining heat treatment parameters and designing new alloys. The kinetics involved in homogenization heat treatment includes diffusion of solute on both of the inter-precipitate scale (10-100 nm) and secondary arm spacing scale (~10 μm). The least mature theory involved here is for nucleation. This is reflected by the different nucleation mechanisms reported in the literatures for the same alloy system, the lack of accurate information on the key property parameters such as interfacial energy and thermodynamic driving force, and the difficulties to observe the nucleus during the early stage of precipitation. Nevertheless, multi-scale numerical models, developed on the basis of thermodynamics and kinetics theory and validated by necessary experimental measurements, has been proved to be valuable in explaining those complex phenomena observed experimentally.

There have been many approaches to simulate the microstructural evolution during solidification and homogenization heat treatment of aluminum alloys. They could be divided into two categories: direct detailed approaches and physically-based internal state variable approaches [4]. Due to the restrictions from computational power, physically-based state variable methods are more suitable to simulate many industrial relevant precipitation processes than the direct detailed numerical approaches represented by the popular phase field method. Examples include modeling the formation of dispersoids free zone during homogenization heat treatment of AA3xxx alloys [3], the up-quenching of AA6060 alloys [5], and the computation of time-temperature-precipitation diagrams of industrial alloys [6]. A common feature of these problems is concurrent nucleation, growth, coarsening, which may be accompanied by larger scale transportation phenomenon (diffusion, heat transfer etc). They have been addressed in an adequate manner by the physically-based numerical model pioneered by WAGNER and KAMPMANN (KWN) [7].

The KWN model is one of the two major components of the comprehensive homogenization heat treatment model reported in Ref. [3]. The essence of the Kampmann and Wagner numerical (KWN) model as well as its later variants [5,8-13] is that the continuous particle size distribution (PSD) curve is subdivided into size classes, each of which is associated with the number of identical precipitates. The temporal evolution of size distribution is then tracked by following the evolution of each discrete class. The latest development of this model is its coupling with calculation phase diagram [13], which enables its application to industrial multi- component alloys.

Although the latest KWN model is computationally efficient [13], it is still challenging to model the effect of minor alloying elements, such as Cr and Zn on microstructural evolution. The difficulties originate from the huge disparity in diffusivity (two to four orders of magnitude) between these alloying components and the main alloying element, Mn [14]. The aim of this work is to extend the KWN model to model the effect of Cr and Zn on microstructure evolution during homogenization heat treatment of AA3xxx alloys. This wrok attempts to apply one of the sub-models of the comprehensive modeling approach reported in Ref. [3], i.e., dispersoids precipitation modeling, to address the effect of impurities on microstructure evolution. In order to do that, minor modification of the original model has been made, which is essential to apply the comprehensive modeling framework to recycled aluminium alloys.

2 Model descriptions

The CALPHAD-coupled KWN model described in Ref. [13] forms the base for the proposed model. The main assumptions adopted in the extended model include:

1) Precipitates are in spherical shape and their growth/dissolution is solely controlled by diffusion in the matrix phase.

2) Local equilibrium modified by the Gibbs- Thomson effect prevails at the precpitate-matrix interface.

3) The diffusion field surrounding each growing precipitate is at quasi-steady state.

Mathematically, the model consists of three sets of equations. The first set of equations are derived from the solute conservation law, which accounts for the enrichment/depletion resulted from precipitate growth.

Considering precipitation in a supersaturated matrix phase with its volume denoted by V_Domain and nominal composition by , the following equation can be written for the alloying component I (1≤i≤N, the total number of alloying components):

    (1)

where R_j,  and  are the radius, average composition and the number of the precipitates associated with size class j; N_OS is the total number of  precipitate size classes;  is the average matrix composition of element i. In our notation, the superscripts *, β, and α represent the interfacial, precipitate and matrix quantities, respectively. The subscript i is for component i. The compositional profile of component i across a precipitate is approximated as either “freezing” (non-diffusion) or “uniform” (extremely quick diffusion), and  is related to the interfacial solid phase composition, 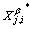, by one of the following equations:

  (2a)

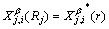                         (2b)

The second set of equations come from the interfacial local equilibrium (modified by the Gibbs- Thomson effect) assumption. For size class j, it can be written as

                             (3a)

                          (3b)

where T^α represents solvus temperature and represents k partition coefficient. This equation relates the interfacial phase compositions via partition coefficients and solvus temperature. The proposed model employs CALPHAD method and a look-up table technique for efficient phase diagram data access [3]. It requires the creation of a mapping table where the discrete phase diagram data points are saved. The creation of the mapping table requires a thermodynamic database and a Gibbs-energy minimizer used in CALPHAD software. A multi-linear interpolation technique is then used to estimate values between the discrete points. The table-look-up technique transforms the iterative calculation of phase diagram data (partition coefficients and solvus temperature) into a table look-up and interpolation procedure, therefore requiring much less computational time.

The third set equations are precipitate growth rate equation. It is deduced from invariant field approximation [15] and is written for alloying component i:

                                   (4a)

                            (4b)

where D_i and Ω_i are the diffusivity and dimensionless super-saturation of component i, respectively;is the bulk melt composition. In a multi-component system, multiple growth rate equations exist, together with the local equilibrium assumption to determine the interfacial compositions and growth rate. This has been explained in Ref. [13]; if the solutes have different diffusivities, the tie-line joining the interfacial compositions of the alloying components does not pass through the bulk composition. This allows the supersaturations of the components to differ such that growth rate has the same value for each solute.

Nucleation model is an essential part of the KWM model but it still remains as the bottle neck for quantitative predictions. Careful experimental validation is still required. Classical models for nucleation are generally referred to as either “homogeneous” or “heterogeneous” and the later prevails under the scenario considered in this work. The physical property parameters required to compute the nucleation rate of dispersoids are the number of nucleation sites per unit volume, the interfacial energy, the diffusivity of an alloying element in the matrix, the volumetric thermodynamic driving force for precipitate, the matrix mean solute atom fraction, the mean atomic volume within precipitates and the lattice parameter of the matrix phase. It is referred to Ref. [16] for more details on the nucleation model.

3 Results and discussion

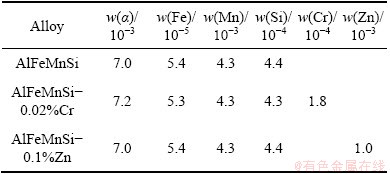
The AA3xxx alloy under investigation contains 0.048%Fe, 0.50%Mn, 0.1%Si (in mole fraction) with either 0.02%Cr or 0.1%Zn as impurity. The Cr and Zn additions exert their influence on precipitation kinetics via their thermodynamic and diffusional kinetic contribution. Table 1 lists how the additions of these two components influence thermodynamic equilibrium at a typical heat treatment temperature of 600 °C. The noticeable observation is that Zn increases Fe solubility and has little influence on Mn solubility while Cr increases precipitation phase fraction slightly by partitioning to precipitation phase. The input parameters for all the simulations are listed in Table 2.

Table 1 Effect of Cr and Zn additions on thermodynamic equilibrium of AA3003 alloy at 600 °C (composition: 0.0484%Fe, 0.50818%Mn, 0.099153%Si)

As shown in Fig. 1, the addition of Cr slows down slightly coarsening kinetics and leads to a lower dispersoids phase fraction. The addition of Zn has very little effect on coarsening kinetics. Overall their effects are not significant. The small plateau appearing at about 6.3 h of heat treatment is due to the dissolution of dispersoids induced by the increase of temperature. Oscillations in the three curves are present after 20 h of heat treatment, which could be eliminated by increasing the number of size classes used in the simulation.

Due to its low diffusivity at nucleation temperature (300 °C), Cr induces very long incubation time, which is prohibitive to nucleate at 300 °C. This might induce significant effect on microstructural evolution. However, in the simulation, Cr was excluded from the incubation time calculation. It will be an interesting topic to have a nucleation model which could take into account these slowing diffusing components. Another interesting topic for further investigation is to link what the model predicts with the experimental observation regarding the nucleus compositions.

The simulation is also able to reveal how dispersoids composition evolves during the heat treatment. The AA3003 alloy without the additions of Cr and Zn is taken for illustration. Initially dispersoids contains more Fe than Mn since Fe diffuses faster than Mn (Fig. 2). However, it decreases as Fe depletes and Mn becomes mobile with the increase of temperature. The increase of Fe (and the decrease of Mn) composition in dispersoids between 6.5 h and 10 h is due to the adjustment of precipitate composition to the temperature change, i.e., the solubility of Mn in FCC increases quicker than that of Fe with the increase of temperature.

Table 2 Numerical parameters and thermo-physical parameters used for simulation

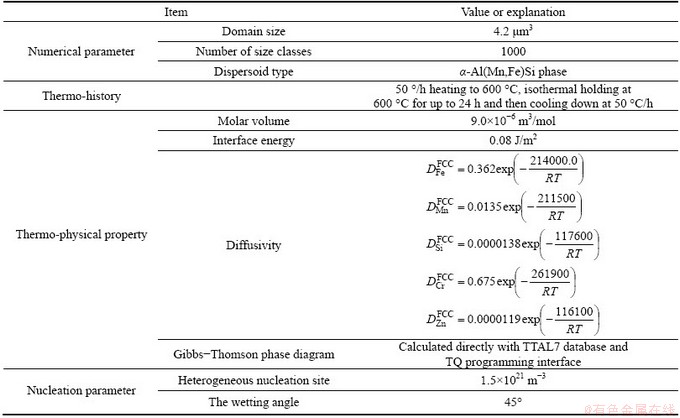
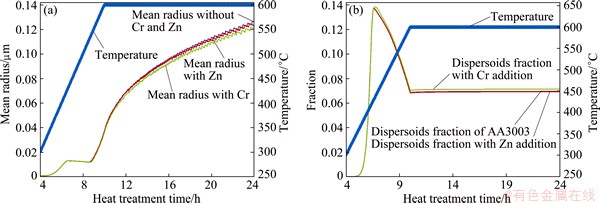
Fig. 1 Predicted effect of Cr and Zn on evolution of mean size (a) and dispersoids fraction (b) during homogenization heat treatment of AA3003 alloy

4 Conclusions

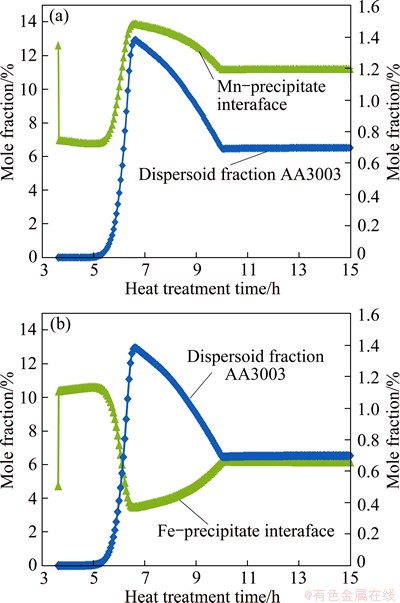
Fig. 2 Evolution of Mn (a) and Fe (b) composition in dispersoid during heat treatment of AA3003 alloy

The CALPHAD-coupled modeling approach is employed to investigate the effect of minor additions of alloying components such as Cr and Zn. The simulation is able to reveal the behavior of each alloying component during nucleation, growth and coarsening, e.g, the partitioning of an alloying component at the moving precipitation-matrix interface, which is very difficult to characterize experimentally. With the further improve-ment on nucleation model, the proposed model has the potential to guide the design or optimization of the chemical compositions and heat treatment procedures of commercial aluminum alloys.

References

[1] LI Y J, ARNBERG L. Quantitative study on the precipitation behavior of dispersoids in DC-cast AA3003 alloy during heating and homogenization [J]. Acta Materialia, 2003, 51: 3415-3428.

[2] ENGLER O, LAPTYEVA G, WANG N. Impact of homogenization on microchemistry and recrystallization of the Al-Fe-Mn alloy AA 8006 [J]. Materials Characterization, 2013, 79: 60-75.

[3] DU Q, POOLE W J, WELLS M A, PARSON N C. Microstructure evolution during homogenization of Al-Mn-Fe-Si alloys: Modeling and experimental results [J]. Acta Materialia, 2013, 61: 4961-4973.

[4] GRONG O, SHERCLIFF H R. Microstructural modeling in metals processing [J]. Progress in Materials Science, 2002, 47: 163-282.

[5] MYHR O R, GRONG O. Modelling of non-isothermal transformations in alloys containing a particle distribution [J]. Acta Materialia, 2000, 48: 1605-1615.

[6] ROBSON J D, JONES M J, PRANGNELL P B. Extension of the N-model to predict competing homogeneous and heterogeneous precipitation in Al-Sc alloys [J]. Acta Materialia, 2003, 51: 1453-1468.

[7] WAGNER R, KAMPMANN R. Homogeneous second phase precipitation [M]//CAHN R W. Materials Science and Technology: A Comprehensive Treatment. Weinheim: John Wiley & Sons Inc, 1991.

[8] MAUGIS P, GOUNE M. Kinetics of vanadium carbonitride precipitation in steel: A computer model [J]. Acta Materialia, 2005, 53: 3359-3367.

[9] ROBSON J D. Modelling the overlap of nucleation, growth and coarsening during precipitation [J]. Acta Materialia, 2004, 52: 4669-4676.

[10] GANDIN C A, JACOT A. Modeling of precipitate-free zone formed upon homogenization in a multi-component alloy [J]. Acta Materialia, 2007, 55: 2539-2553.

[11] PEREZ M, DUMONT M, ACEVEDO-REYES D. Implementation of classical nucleation and growth theories for precipitation [J]. Acta Materialia, 2008, 56: 2119-2132.

[12] KAMP N, SULLIVAN A, TOMASI R, ROBSON J D. Modelling of heterogeneous precipitate distribution evolution during friction stir welding process [J]. Acta Materialia, 2006, 54: 2003-2014.

[13] DU Q, POOLE W J, WELLS M A. A mathematical model coupled to CALPHAD to predict precipitation kinetics for multicomponent aluminum alloys [J]. Acta Materialia 2012, 60: 3830-3839.

[14] DU Y, CHANG Y A, HUANG B Y, GONG W P, JIN Z P, XU H H, YUAN Z H, LIU Y, HE Y H, XIE F Y. Diffusion coefficients of some solutes in fcc and liquid Al: Critical evaluation and correlation [J]. Materials Science and Engineering A, 2003, 363(1-2): 140-151.

[15] AARON H B, FAINSTEIN D, KOTLER G R. Diffusion-limited phase transformation: A comparison and critical evaluation of the mathematical approximations [J]. Journal of Applied Physics, 1970; 41(11): 4404-4410.

[16] RUSSELL K C. Nucleation in solids: The induction and steady state effects [J]. Advances in Colloid Interface Science, 1980, 13: 205-318.

Cr和Zn元素对AA3xxx合金均质化热处理微观组织演化的模拟研究

杜 强¹，李彦军²

1. SINTEF Materials and Chemistry, 7465 Trondheim, Norway;

2. Department of Materials Science and Engineering, NTNU, 7491 Trondheim, Norway

摘  要：Cr和Zn作为杂质或添加合金元素对铝合金产品的最终性能有很大影响。采用基于热力学与扩散动力学的KWN模型，研究了这两种元素对AA3xxx合金均质化热处理过程中弥散相形成的影响。该研究的目的是展示数学模型对铝合金成分及工艺设计的指导作用。

关键词：均质化热处理；数学模型；CALPHAD；扩散；Kampmann-Wagner模型

(Edited by Hua YANG)

Corresponding author: Qiang DU; E-mail: Qiang.du@sintef.no

DOI: 10.1016/S1003-6326(14)63325-2