J. Cent. South Univ. Technol. (2011) 18: 1193-1199

DOI: 10.1007/s11771-011-0822-3

New algorithm for variable-rate linear broadcast network coding

XIA Yin(夏寅)^{1, 2}, ZHANG Ti-yuan(张惕远)^{1, 2}, HUANG Jia-qing(黄佳庆)^{1, 2}

1. Department of Electronics and Information Engineering,

Huazhong University of Science and Technology, Wuhan 430074, China;

2. Hubei Provincial Key Laboratory of Smart Internet,

Huazhong University of Science and Technology, Wuhan 430074, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: To adjust the variance of source rate in linear broadcast networks, global encoding kernels should have corresponding dimensions to instruct the decoding process. The algorithm of constructing such global encoding kernels is to adjust heterogeneous network to possible link failures. Linear algebra, graph theory and group theory are applied to construct one series of global encoding kernels which are applicable to all source rates. The effectiveness and existence of such global encoding kernels are proved. Based on information flow, the algorithm of construction is explicitly given within polynomial time  and the memory complexity of algorithm is O(|E|). Both time and memory complexity of this algorithm proposed can be O(ω_max) less than those of algorithms in related works.

Key words: network coding; variable-rate; linear broadcast; heterogeneous network; code construction algorithm

1 Introduction

Network coding theory was proposed in order to achieve the maximum capacity of network, which can hardly be realized in conventional router-based network [1-6]. AHLSWEDE et al [7] have proved that network coding can achieve the multicast capacity. LI et al [8] and KOETTER et al [9] have proved that linear network coding suffices to guarantee the optimum data transmission in multicast problems, which spurs hot research on linear network coding. Four kinds of properties of linear network codes are proposed in network coding theory [1], that is, linear multicast, linear broadcast, linear dispersion, and generic linear network code. Furthermore, linear information ?ow (LIF) algorithm constructing the multicast network is devised in polynomial time [10]. These properties are arranged by the strength of independence among global encoding kernels in an increasing manner. HO et al [11] have made network coding feasible by proposing random network coding.

Linear broadcast network coding has distinct property of regarding all non-source nodes as destination nodes and provides them with different services according to their qualifications. Thus, it is potential for various applications, especially in heterogeneous networks [12]. Theories on network coding adapted to broadcast channels are researched [13]. On the other hand, the con?guration of a communication network might vary from time to time due to tra?c congestion, link failure, etc [1]. Static network codes are defined to handle such condition by constructing codes for all possible cases of link failures. The algorithms have been proposed in Refs.[1-14]. However, time complexity and space complexity are expected to be further reduced.

Linear broadcast network has been investigated for years; however, little was done on the scenario of such networks with variable-rate source until FONG et al [15] pioneered the research. With the method of linear network coding, FONG et al proposed concepts of variable-rate network, and studied linkages among linear broadcasts of different rates. Also, they considered variable-rate network with link failures for the first time and gave the algorithm of constructing such network codes. GOSELING et al [16] searched for minimum-cost multicasting using the concepts of variable-rate network coding. These works generally focused on undertaking modifications on global encoding kernels according to the change of source node. Further, GUO et al [17] gave the algorithm explicitly and proposed an alternative method of searching for reduction vector. Recently, MA et al [18] researched the variable-rate convolutional network coding, which is a variable-rate network coding in cyclic network. The concept of reduction vector is still valid in cyclic network when incorporating mathematic concepts of discrete valuation ring (DVR). Static linear broadcast was similar to network codes in Ref.[15], which stored many global encoding kernels for various configurations so that nodes could still receive message according to their capacities. Static linear broadcast codes considered all possible configurations, and the complexity was expected to be reduced.

Unlike the previous related works, the variance of source rate is first viewed as the result of changes in network link states. In order to maintain the characteristic of linear broadcast network, i.e., every node has to receive message according to its maxflow, codes need to be adapted to this variance. Instead of mapping global encoding kernel to lower dimensions as the conventional algorithm, a series of linear broadcast codes are expected to be adaptive to all possible source rates. This new perspective contributes to the new algorithm of constructing such variable-rate network codes. In this work, constant network codes applicable to network with various source-rates are proposed, and the algorithm of constructing such variable-rate linear broadcast codes within polynomial time is given.

2 Preliminaries

A communication network is modeled as an acyclic directed graph denoted by G=(V, E), where V is node set and E is the edge set. Suppose edges in the network are in unit-capacity and free of delay. Only one source node, denoted by S, transmits symbol through the network at one time session. The maximum ?ow from the source S to a destination node T is denoted by max?ow(T). In(T) and Out(T) are denoted as set of edges going in and out of the node T. Let In(S) denote a set of imaginary channels, which terminate at the source node S but without originating nodes. A pair of edges (d, e) is called adjacent pair if dIn(T) and eOut(T) where T is a node in G. d is the predecessor of e. Path from edge e_{1, 2} to edge e_{m-1, m} is a sequence of adjacent pairs e_1,2, e_2,3, …, e_m-1,m. Paths are edge-disjoints when they do not have any edge in common. De?ne “index” as an identification  such that edge e is on the j-th information flow path for destination node T_i. A set of global encoding kernels  are linearly independent and these global encoding kernels are on different edge-disjoint information flow paths generated from the source to destination node T_i. A formal definition of linear network coding is given as follows.

De?nition 1: linear network coding [1]

Let F be a positive integer which represents a ?nite ?eld. On an acyclic communication network, a scalar k_(d,e) is defined as local encoding kernel for adjacent pair (d, e) in the network, and an ω-dimension column vector f_e is defined as global encoding kernel for every edge e in the network. An ω-dimensional F-valued linear network code consists of local encoding kernels and global encoding kernels such that

1)  eOut(T);

2) The vector f_e for the imaginary channel eIn(S) is form the natural basis of the vector space F_ω.

Global encoding kernel indicates the relationship between received symbol and the source, which is calculated recursively in upstream to downstream order:

[X₁, X₂, …, X_ω]?f_e=σ_e

σ_e is the symbol received by a destination node T_i. The decoding procedure would follow the Crammer rule and operate on an augmented matrix. Denote the augmented matrix as A, which is formed by juxtaposing every global encoding kernel  (1≤j≤ω) entering the destination node T_i. The mathematical expression of decoding procedure is

where C(?) is the column operation on matrix A, so that

X_i (1≤i≤ω) is the decoded message, the same as the source message. Further, we specify our discussion on linear broadcast. In this sort of network, it always follows the principle that “nodes with more mincuts will receive more message and nodes with less mincuts will get less”. The formal definition is given as follows.

De?nition 2: Linear broadcast network code [1]

Let vector f_d denote the global encoding kernel in an ω-dimension F-valued linear network code on a single-source ?nite acyclic network. Let V_T denote the set of global encoding kernels on the entering edges of non-source node T:

V_T=span {f_d: dIn(T)}

Then, the linear network code quali?es as a linear broadcast if the following formula holds for every non-source node T:

dim(V_T=min{ω, max?ow(T)}

In addition, it is necessary to define the notion of “rate”. Generally, rate is the number of source messages per time unit. In a mathematic perspective, rate ω is the number of imaginary channels. Because of the changes in link states of the network, certain area of network may receive fewer pieces of messages from the source, which can be viewed as source rate reduction of the area. It is reasonable to assume that the maximum rate of source is ω_max. Global encoding kernels applicable to various source rates are defined as linear variable-rate network codes.

De?nition 3: Variable-rate linear broadcast network code

This is the formal definition for new variable-rate linear broadcast network codes.

Let vector f_d denote the global encoding kernels in an F-valued variable-rate linear broadcast network with rate of ω≤ω_max. Let M_T denote the matrix spanned by global encoding kernels on edges entering non-source node T:

M_T=[f_d: dIn(T)]

According to Definition 2, M_T is a matrix with rank equal to min{ω, max?ow(T)}. For network code defined as variable-rate linear broadcast code, which is applicable to various rates in linear broadcast network, it is also required that the matrix M_T remains full-rank after any number of rows is removed from them (from bottom to top). That is, with the change of source-rate, it always follows

Rank(M_T)=min{ω, max?ow(T)}, ω≤ω_max

It is obvious that variable-rate linear broadcast has stricter requirement of linear independence on global encoding kernels than conventional linear broadcast, i.e. linearly independent in required dimensions.

3 Construction of variable-rate network coding

This algorithm constructs variable-rate linear broadcast network codes with the maximum dimension of ω. Only one series of global encoding kernels and local encoding kernels will guarantee a linear broadcast according to different rates of the source.

3.1 Algorithm

1) Main-routine

(1) Initialization of network codes: For every edge e in the network with dimension ω, except for imaginary channels in In(S), there is

(2) By de?ning “index”  to indicate an edge- disjoint path  for non-source nodes T_i, the related paths  for nodes T_i have been determined. For all indices of every non-source node,  is the global encoding kernel initiating the path .

(3) For every node in upstream-to-downstream order, select every edge eOut(T), whose predecessors have been determined.

(4) Choose a vector ν in V_T, V_T=á{f_d:dIn(T)}?, and call sub-routine so that ν could satisfy the demand of independence for all nodes related.

(5) Set f_e=ν, which is equivalent to determining a scalar value for local encoding kernel k_(d,e) for all dIn(T)

such that the vector  and every sub-vector  of  f_e follows .

2) Sub-routine

(1) For the channel e, ?nd all related indices  which represent demand of independence for all related destination nodes T_i. Denote m=maxflow(T_i);

2) Verify that m-dimensional subvector  follows

where  is sub-vector derived from the chosen ω-dimensional vector ν by eliminating (ω-m) elements from the bottom to the top. This verification is implemented by calculating the ranks of all m×m matrix  which consists of juxtaposed vectors of global encoding kernels for “indices” of nodes T_i;

(3) If every rank()=m, then ν can be used as the global encoding kernel for this channel. Return to step (5) in main-routine;

Else if there is rank() contains zero vector which is not the encoding channel, that is, judge whether  is 0, i.e., an m-dimensional zero vector. If this is true, the problem can be handled by modifying other channels while ignoring this violation of independence. Return to step (5) in main-routine;

Else, there is rank()

3.2 Justification of algorithm

The justification is given that the code generated by the algorithm is indeed a “variable-rate linear broadcast code” and such code exists if the variable-rate linear broadcast has sufficient large field.

1) Lemma: Property of variable rate network code

(1) In a network with maximum rate ω_max, for nodes with maxflow(T_i)≥ω_max, the edges entering T with ω_max linearly independent global encoding kernels will guarantee that these multicast nodes successfully decode in all rates less than ω_max.

(2) In a network with rate ω_max, for nodes with maxflow(T_i)<ω_max, once their related global encoding kernels are linearly independent in m dimension, where m equals the maxflow of the node, the characteristic of linear broadcast will maintain in all rates less than m.

Proof:

(1) For nodes with maxflow(T_i)≥ω_max, it is obvious

that  has

Rank()=ω_max

By reducing the last k rows of the matrix  it should follow that the (ω_max-k)×ω_max matrix  has Rank()=ω_max-k. In perspective of network coding, it

means that when the rate changes from ω_max to (ω_max-k), the dimension and number of global encoding kernels on imaginary channels will be (ω_max-k), and original nodes with maxflow≥ω_max can still receive all messages from the source.

(2) It is similar when considering the nodes with maxflow less than ω_max. For these nodes, the ω_max×m matrix of global encoding kernels

has Rank()=maxflow(T_i)=m

By reducing the last k rows of matrix if ω_max-k≥m, then Rank()=maxflow(T_i)=m. If ω_max-k≤ m, then Rank()=maxflow(T_i)=ω_max-k. In sum, Rank()=min{maxflow(T_i), ω}, where ω is the current source rate. This indicates that the characteristic of linear broadcast still maintains. Thus, it is verified that the variable-rate network code can adopt various source rates in the network.

2) Theorem: Existence of variable rate network code

For network with maximum rate ω_max, 2≤ω≤ω_max, if field size |F|>|T|-|T_maxflow=1|+1 (|T| is the total number of non-source nodes, |T_maxflow=1| is the number of destination nodes with max-flow equal to one), a global encoding kernel  for an edge e can be found to satisfy the following requirement:

For every index  on edge e, denote max?ow(T_i)=m, where m-dimensional sub-vector of  denoted by  is linearly independent with all related global encoding kernels in dimensions of m: .

Proof:

For an edge e searching for a global encoding kernel, there are many indices  which indicate that the global encoding kernel  on this edge should satisfy the requirements of linear independence for all indices. Denote that the tail of edge e is T_e, and the linear space

of T_e is  Consider the strictest requirement of linear

independence for this edge e: every non-source node has an information flow path on this edge. However, as nodes with maxflow equal to 1 will have at most one information flow path from the source, they have only one index. This means at most one node with maxflow equal to 1 has index on edge e. Thus, the number of indices on this edge is at most |T|-|T_maxflow=1|+1. Suppose that all other global encoding kernels which are associated with indices on edge e have been chosen. For every non-source node T_i : i≤|T|, the dimension of used vectors should follow

min{maxflow(T_e), maxflow(T_i)}-1

 represents all related global encoding kernels that should be linearly independent with  Note that if ω=1, no coding is necessary because all messages are the same.

Further, it can be concluded that the number of global encoding kernels chosen from the field is

≤

1+|T_maxflow=2|×|F|+…+

+…+

Therefore, the remaining number of global encoding kernels in the field is

This means that there are always qualified vectors that can be chosen from the field for a certain edge in the network. Thus, it could be concluded that this algorithm is valid to construct variable-rate linear broadcast network.

4 Example of constructing variable-rate linear broadcast

The proposed algorithm is applied in an example of heterogeneous network with link failures. The topology graph of network is shown in Fig.1. In this network, there are eight non-source nodes denoted by T_i:1≤i≤8 and single source node S with rate of 4, represented by four imaginary channels. One source node transmits messages to all eight non-source nodes with different maxflows. Link failures are possible in this network, which may result in the reduction in maxflows of destination nodes. For example, failure in the link between destination node T₄ and destination node T₈ will result in maxflow change of node T₈ from 4 to 3. For node T₈, the change of maxflow caused by link failures is regarded as the reduction of source rate. New global encoding kernels with three dimensions corresponding to source node can instruct the decoding procedure for destination node T₈.

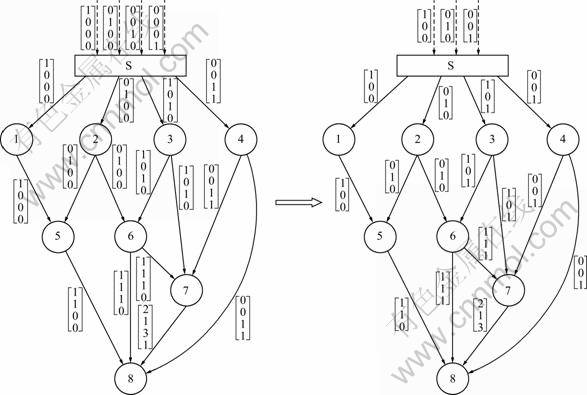
Fig.1 Topology of heterogeneous network with applying proposed algorithm

As there are four non-source nodes with max?ow of 1, set the ?eld |F|=6>8-4+1=5. The maxflow of non-source nodes is as follows.

1) max?ow(T_i:1≤i≤4)=1, indicating that global encoding kernels entering these nodes should not be all zero vectors;

2) max?ow(T_i: 5≤i≤6)=2, indicating that set   are independent sets consisting of two-dimensional sub-vectors;

3) max?ow(T₇)=3, indicating that   is independent set consisting of three- dimensional sub-vectors;

4) max?ow(T₈)=4, indicating that set   is independent set consisting of four- dimensional vectors.

The operating steps are as follows.

1) Initiate global encoding kernels: for every edge in the network f_e=[0 0 0 0]^T.

2) Initiate indices of every non-source node by global encoding kernels on imaginary channels:

3) Encode the edge going out of node, starting from the edge from S to T₁.

4) Choose initiated vector [1 0 0 0]^T to this edge and go to the sub-routine:

(1) The related indices are   ,

(2) Thus, the matrices whose ω-min{ω, maxflow(T_i)} rows are eliminated are

2= maxflow(T₅), 4 =  maxflow(T₈). This is the case of (3) in sub-routine.

(3) Thus, vector chosen is qualified, and go to the step (5) in main-routine.

5) Set f_e=[1 0 0 0]^T. Move on to the edge from S to T₂.

Procedures of the algorithm will continue in this way until the last edge is coded. Here, we describe another encoding procedure for the edge from S to T₃ because another judging condition in the algorithm will be encountered.

1) and 2) are the initiating steps that only implement once. Thus, encoding procedure for the edge from S to T₃ starts from the “For” loop in step 3):

3) Encode the edge from S to T₃;

4) Choose initiated vector [0 0 1 0]^T to this edge and go to the sub-routine:

(1) The related indices are   

(2) Thus, the eliminated matrices are

(3) It can be calculated that Rank()=1< maxflow(T₆), Rank()=27), Rank()= 4=maxflow(T₈). Note that although Rank()=2< maxflow(T₇), zero vector 0 is the global encoding kernel on another edge, and the linear dependence could be ignored. However, Rank()=16) while global encoding kernel on other edges is not zero vector.

Thus, go to the step (4) in the main-routine and search for another vector.

Vector [1 0 1 0]^T will be searched to satisfy the requirements of ranks for ,  and .

5) Set f_e=[1 0 1 0]^T, and move on to the next edge;

In the end, all global encoding kernels are set. The same network with a reduced rate can still use the original global encoding kernels after reducing the last row, as shown in Fig.1.

5 Complexity analysis

The complexity of the new algorithm is analyzed and compared with algorithms of related works.

Initialization in step 1) has time complexity of O(|E|), where |E| is the number of edges in the network. In addition, inverse vector a proposed in RLIF will be used here to test the linear independence. Inverse vector a will also be initialized and the complexity is  [10]. Step 2) initializes global encoding kernels for all indices, which takes O(ω_max·|T|). Steps 3) and 4) will choose a vector in linear space V_T=á{f_d: d In(T)}?, and call sub-routine to judge the qualification of this vector.

The sub-routine is the main difference between algorithms in this work and others. Steps 1) and 2) construct the matrix, then step 3) tests linear independence quickly, which takes  As it is a constant possibility for the chosen global encoding kernel to be not linearly independent with other global encoding kernels in a fixed rate [10], it is also a constant possibility for the chosen global encoding kernel to be linearly independent with other global encoding kernels in different dimensions. Thus, all testing running time will be O(?|T|)·O(1). Since sub-routine will execute for O(|E|) times, the time complexity is O(|E|·|T|· Adding all complexity of running time, it is calculated that the complexity of algorithm in this work is O(|E|·|T|·

On the other hand, algorithms in related works [15, 17] search for reduction vectors for all possible rates less than ω_max so as to maintain the characteristic of linear broadcast. The complexity of constructing procedure for each rate is similar to RLIF, thus the complexity is  It could be concluded that the complexity of algorithms in related works is approximately ω_max times larger than the complexity of the algorithm in this work.

Also, the memory complexity of algorithms in related works is larger than that of algorithm in this work. In the procedures of constructing codes for an edge, algorithms in related works have to store all possible reduction vectors so that the common reduction vector for all edges can be selected. In addition, the global encoding kernels of all ω_max rates have to be stored in all |T| destination nodes. Therefore, the complexity of memory is O(ω_max?|E|). Algorithm in this work abandons the concept of reduction vector, so no memory for that is necessary. Also, only one set of global encoding kernels is necessary, and the memory complexity is O(|E|). Thus, the memory consumption in related works will be O(ω_max) larger than that of the algorithm in this work.

6 Conclusions

Link failure scenario is assigned under the mathematical frame of variable-rate linear network coding. The new algorithm constructs a series of global encoding kernels applicable to all source rates within polynomial time The memory complexity of this algorithm is O(|E|).

References

[1] YEUNG R W, LI S R, CAI Ning, ZHAG Zhen. Network coding theory [M]. Boston-Delft: Now Publisher Inc, 2005: 11-50.

[2] YEUNG R-W. Information theory and network coding [M]. New York: Springer, 2008: 411-541.

[3] YANG Yi-xian. Network coding theory and technology [M]. Beijing: National Defense Industry Press, 2009: 1-229. (in Chinese)

[4] FAN Ping-yi. Network information theory [M]. Beijing: Tsinghua University Press, 2009: 109-147. (in Chinese)

[5] FRAGOULI C, SOLJANIN E. Network coding fundamentals [J]. Foundations and Trends in Networking, 2007, 1(2): 1-133.

[6] HO T, LUN D S. Network coding: An introduction [M]. Cambridge, UK: Cambridge University Press, 2008: 13-85.

[7] AHLSWEDE R, CAI Ning, LI S R, YEUNG R W. Network information ?ow [J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.

[8] LI S R, YEUNG R W, CAI Ning. Linear network coding [J]. IEEE Transactions on Information Theory, 2003, 49(2): 371-381.

[9] KOETTER R, MEDARD M. An algebraic approach to network coding [J]. IEEE Transactions on Networking, 2003, 11(5): 782-795.

[10] JAGGI S, SANDERS P, CHOU P A, EFFROS M, EGNER S, JAIN S, TOLHUIZEN L, Polynomial time algorithms for multicast network code construction [J]. IEEE Transactions on Information Theory, 2005, 51(6): 1973-1982.

[11] HO T, MEDARD M, KOETTER R, KARGER D, EFFROS M, SHI J, LEONG B. A random linear network coding approach to multicast [J]. IEEE Transactions on Information Theory, 2004, 52(10): 4413-4430.

[12] MA W Y, BEDNER I, CHANG G., KUCHINSKY A, ZHANG H J. A framework for adaptive content delivery in heterogeneous network environments [C]// Proc 2000 MMCN. San Jose, USA, 2000: 86- 100.

[13] SADEGHI P, TRASKOV D, KOETTER R. Adaptive network coding for broadcast channels [C]// Workshop on Digital Object Identifier NetCod. Lausanne, Switzerland, 2009: 80-85

[14] LI S R, CAI Ning, YEUNG R W. On theory of linear network coding [C]// ISIT Inf Theory. Adelaide, Austrialia, 2005: 273-277.

[15] FONG S L, YEUNG R W. Variable-rate linear network coding [C]// Information Theory Workshop. Puntadel Este, Uruguary, 2006: 409- 412.

[16] GOSELING J, WEBER J H. Multi-rate network coding for minimum-cost multicasting [C]// IEEE Symposium on Information Theory. 2008: 36-40.

[17] GUO Qin, ZHUO Xin-jian, MA Song-ya, LUO Ming-xing, YANG Yi-xian. Algorithms of variable-rate linear network coding [C]// Proc of Triangle Symposium on Advanced ICT. Daejeon, Republic of Korea, 2008: 1-6.

[18] MA Song-ya, CHEN Xiu-bo, LUO Ming-xing, YANG Yi-xian. Variable-rate Convolutional network coding [J]. The Journal of China Universities of Post and Telecommunications, 2010, 17(3): 91-96.

(Edited by YANG Bing)

Foundation item: Project(60872005) supported by National Natural Science Foundation of China

Received date: 2010-04-30; Accepted date: 2010-11-24

Corresponding author: ZHANG Ti-yuan, PhD candidiate; Tel: +86-13871006121; E-mail: zhangty@mail.hust.edu.cn