Trans. Nonferrous Met. Soc. China 23(2013) 1090-1097
Theoretical prediction of effective elastic constants for new intermetallic compound porous material
Shu-lan SU1,2, Qiu-hua RAO1, Yue-hui HE3
1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. College of Civil Engineering and Mechanics, Central South University of Forestry & Technology, Changsha 410004, China;
3. Powder Metallurgy Research Institute, Central South University, Changsha 410083, China
Received 16 March 2012; accepted 8 January 2013
Abstract: Based on microstructure analysis of the new Ti-Al intermetallic compound porous material, a micromechanics model of heterogeneous Plateau porous structure was established and calculation formulas of elastic constants (including effective elastic modulus, effective shear elastic modulus and effective Poisson ratio) were derived by the energy method for this porous material. Calculation results show that both the effective elastic modulus and effective shear elastic modulus increase with the increase of the relative density while the effective Poisson ratio decreases. Compared with the currently-existing hexagonal honeycomb model and micromechanics model of composite materials, the micromechanics model of heterogeneous Plateau porous structure in this study is more suitable for characterizing the medium-density porous material and more accurate for predicting the effective elastic constants of the medium-density porous material. Moreover, the obtained explicit expressions of the effective elastic constants in term of the relative density rather than the microstructural parameters for the uniform and regular Plateau porous structure are more convenient to engineering application.
Key words: intermetallic compound; porous material; effective elastic modulus; Plateau structure; energy method
1 Introduction
Porous material has been widely used in medicine, chemical industry, metallurgy, environmental protection, aerospace and building engineering, owing to its special performance of large specific surface area, high specific mechanical properties, good damping properties and large adsorption capacity, and a variety of functions such as filtration, separation, adsorption, sound-insulation and anti-seism [1-6]. Ti-Al intermetallic compound is a kind of structural material with light weight, high strength and high temperature resistance, but its potential chemical, physical and mechanical properties have not been fully developed. Recently, our research group proposed a new method of element mixture partial diffusion-reactive synthesis-sintering to successfully prepare the Ti-Al intermetallic compound porous material [7], which has advantages of both ceramic and metal porous materials, with higher specific strength and specific modulus, better resistance to high temperature and oxidation [8]. It will be a promising structure and filter material of light weight and high strength.
It is well known that mechanical properties of the porous materials strongly depend on its relative density, pore structure morphology and properties of solid materials. For the low-density porous material of the relative density less than 0.3 (i.e., 0<ρ*/ρs<0.3, where ρ* and ρs are densities of porous and solid materials, respectively), it is usually simplified as interconnected holes or obturator network structure in study of its mechanical properties [9-13]. Elastic mechanics [14] or mechanics of composite material [15,16] is used to study the mechanical properties of the high-density porous material with the relative density larger than 0.8 (i.e., ρ*/ρs>0.8). Ti-Al intermetallic compound porous material prepared by the reaction synthesis is of medium density (i.e., 0.3<ρ*/ρs<0.8). Due to its complexity and heterogeneity of microscopic structure, analytically characterizing the mechanical properties of the medium density porous materials becomes one of the hot and difficult issues in preparation and application of this new material.
In this study, a meso-mechanical model of Plateau porous structure was established based on microstructure analysis of the new Ti-Al intermetallic compound porous material. Calculation formulas of the effective elastic constants (including effective elastic modulus, effective shear elastic modulus and effective Poisson ratio) were derived by the energy method in order to provide theoretical basis for predicting the mechanical properties of the medium-density porous material.
2 Meso-mechanical model of porous structure
The new Ti-Al intermetallic compound porous material is a kind of porous skeleton structure prepared by the three-stage sintering process with characteristics of solid reaction and partial diffusion. It has mostly open pore structure of high relative density (Fig. 1) and can be considered Plateau porous structure [11] with the meso-mechanics model shown in Fig. 2(a). The Plateau porous structure consists of four inclined struts of length (l) and two vertical struts of length (h). In the space coordinate system, the angle between the inclined strut and X1 axis is θ and the thickness of structure in X3 direction is b, smaller than l or h. Because of structural symmetry, the shadow part in Fig. 2(a) is selected to be the representative unit and its detailed size is shown in Fig. 2(b). The geometry size as well as the force and deformation of each strut is symmetrical about its midpoint. It is assumed the strut is isotropic and linear elastic material and the elastic modulus of material is Es.

Fig. 1 SEM image of Ti-Al intermetallic compound porous material
The effective elastic constants (including the effective elastic modulus  and
and  , the effective shear modulus
, the effective shear modulus  and the effective Poisson ratio
and the effective Poisson ratio  ) can be determined based on the displacement, s, of the representative unit in X1-X2 plane calculated by energy method as follows [17]:
) can be determined based on the displacement, s, of the representative unit in X1-X2 plane calculated by energy method as follows [17]:
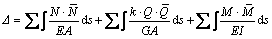 (1)
(1)
where N, Q and M are axial force, shear and bending moment caused by actual load, respectively;  ,
, and
and  are axial force, shear and bending moment caused by virtual unit load, respectively; k is a shear correction coefficient depending on the cross section of the strut.
are axial force, shear and bending moment caused by virtual unit load, respectively; k is a shear correction coefficient depending on the cross section of the strut.
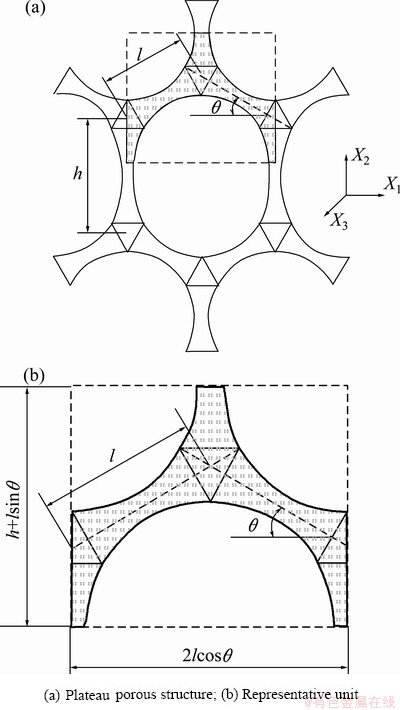
Fig. 2 Meso-mechanics model of porous structure
3 Prediction of effective elastic constants
3.1 Effective elastic modulus  and
and 
btained. quationrtual internal forces of For calculating  in X1 direction, the representative unit is subject to a uniform tensile stress σ1, as shown in Fig. 3(a), and its resultant force in the X1 direction is F1=σ1b(h+lsinθ). The actual internal forces of the inclined strut are Nl =F1cosθ, Ql=F1sinθ and Ml= F1xsinθ, respectively. When a unit load is applied to the representative unit, i.e., F1=1, the virtual internal forces of the inclined strut become
in X1 direction, the representative unit is subject to a uniform tensile stress σ1, as shown in Fig. 3(a), and its resultant force in the X1 direction is F1=σ1b(h+lsinθ). The actual internal forces of the inclined strut are Nl =F1cosθ, Ql=F1sinθ and Ml= F1xsinθ, respectively. When a unit load is applied to the representative unit, i.e., F1=1, the virtual internal forces of the inclined strut become  ,
,  and
and  , respectively. No internal force exists in the vertical strut.
, respectively. No internal force exists in the vertical strut.

Fig. 3 Representative unit subjected to a uniform tensile stress σ1 in X1 direction
The X1-directional displacement of the inclined strut, Δl1, is obtained by substituting the actual and virtual internal forces of the inclined strut into Eq. (1):


Due to the structural symmetry, the X1-directional displacement of the unit is △1=2Δl1, i.e.,

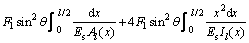 (2)
(2)
The X1-directional linear strain of the unit, ε1, is given by
 (3)
(3)
Therefore, the effective elastic modulus  along the X1 direction is calculated as follows:
along the X1 direction is calculated as follows:

 (4)
(4)
Similarly, the effective elastic modulus  along the X2 direction is given by
along the X2 direction is given by


 (5)
(5)
3.2 Effective shear modulus 
For calculating  in X1 direction, the representative unit is subject to a uniform shear stress τ12 in X1-X2 plane (Fig. 4). Its shear strain in the X1-X2 plane is the sum of the shear strain in the X1 and X2 directions, i.e., γ12=γa+γb. The resultant forces in the X1 and X2 directions are F1=2τ12blcosθ and F2=τ12b(h+lsinθ), as shown in Fig. 5. Therefore, the internal forces of the inclined strut l are Nl=F2sinθ+F1cos(θ/2), Ql=F2cosθ- F1sin(θ/2) and Ml=(F2cosθ-F1sin(θ/2))·x. The internal forces of the vertical strut h are Nh=0, Qh=F1 and Mh=F1·x.
in X1 direction, the representative unit is subject to a uniform shear stress τ12 in X1-X2 plane (Fig. 4). Its shear strain in the X1-X2 plane is the sum of the shear strain in the X1 and X2 directions, i.e., γ12=γa+γb. The resultant forces in the X1 and X2 directions are F1=2τ12blcosθ and F2=τ12b(h+lsinθ), as shown in Fig. 5. Therefore, the internal forces of the inclined strut l are Nl=F2sinθ+F1cos(θ/2), Ql=F2cosθ- F1sin(θ/2) and Ml=(F2cosθ-F1sin(θ/2))·x. The internal forces of the vertical strut h are Nh=0, Qh=F1 and Mh=F1·x.
When a unit load (F1=1) is applied to the representative unit in the X1 direction, the virtual internal forces of the inclined strut l and the vertical strut h are  ,
,  ,
,  and
and  ,
,  ,
,  , respectively.
, respectively.

Fig. 4 Representative unit subjected to a uniform shear stress τ12in X1-X2 plane

Fig. 5 Force analyses of inclined strut l and vertical strut h
According to Eq. (1), the displacements of the inclined strut l and the vertical strut h in X1 direction can be obtained:




The displacement of the unit in X1 direction is δa=δal+δah, i.e.,



 (6)
(6)
Similarly, the displacement of the unit in X2 direction is


 (7)
(7)
The shear strain γ12 of the unit in X1-X2 plane is given by
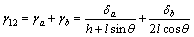 (8)
(8)
Substituting Eqs. (6) and (7) into Eq. (8) results in the effective shear modulus  as follows:
as follows:



 (9)
(9)
3.3 Effective Poisson ratios  and
and 
The effective Poisson ratio  can be calculated by the X1-directional linear strain ε1 shown in Eq. (3) and the X2-directional linear strain
can be calculated by the X1-directional linear strain ε1 shown in Eq. (3) and the X2-directional linear strain 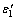 caused by σ1.
caused by σ1.
According to the energy method, the X2-directional linear displacement △12 and linear strain 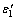 caused by σ1 are
caused by σ1 are

 (10)
(10)
 (11)
(11)
Therefore, the effective Poisson ratio  caused by σ1 is
caused by σ1 is
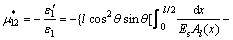


 (12)
(12)
Similarly, the effective Poisson ratio  caused by σ2 is
caused by σ2 is
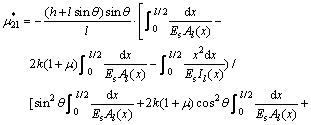
 (13)
(13)
4 Verification
4.1 Effective elastic constants of non-uniform and regular Plateau porous structure
Equations (4), (5), (9), (12) and (13) are calculation formulas for effective elastic constants of the non-uniform and non-regular Plateau porous structure.
For the non-uniform and regular Plateau porous structure of an arbitrary cross section shown in Fig. 2(a), it is supposed that the inclined strut l and vertical strut h have the same length (l=h), and their widths are t(x)=t0[1+α(2x/l)2] (where 0≤x≤l/2, t0 is the width of the struts at the midpoint, and α is a constant larger than zero), the cross-section area is A(x)= t(x)·b and the inertia moment of the cross section is I(x)= t3(x)·b/12. Thus, Eqs. (4), (5), (9), (12), (13) for calculating the effective elastic constants can be simplified as follows:
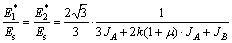 (14)
(14)
 (15)
(15)
 (16)
(16)
where
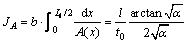 (17)
(17)

 (18)
(18)
The relative density is
 (19)
(19)
Let α=0.5, the width of strut is t(x)=t0[1+0.5× (2x/l)2]. Thus, Eqs. (17)-(19) are reduced to
 (20)
(20)
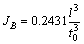 (21)
(21)
 (22)
(22)
By substituting Eqs. (20)-(22) into Eqs. (14)-(16), calculation formulas of the effective elastic constants are obtained for the non-uniform and regular Plateau porous structure:

 (23)
(23)
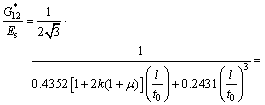
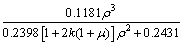 (24)
(24)

 (25)
(25)
4.2 Effective elastic constants of uniform and regular Plateau porous structure
For the uniform and regular hexagonal porous structure, suppose α=0, thus the width of the strut is t(x)=t0, its cross section area is A(x)= t0·b and inertia moment of cross section is I(x)=t03·b/12. Equations (17)-(19) can be simplified as
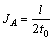 (26)
(26)
 (27)
(27)
 (28)
(28)
By substituting Eqs. (26)-(28) into Eqs. (14)- (16), calculation formulas of the effective elastic constants are obtained for the uniform and regular hexagonal porous structure:

 (29)
(29)

 (30)
(30)

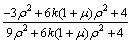 (31)
(31)
4.3 Comparison of this model with currently-existing models
Non-uniform Plateau porous structure model is used both in this study and Ref. [11] for predicting effective elastic constants of porous materials. Our explicit expressions of effective elastic constants in terms of the macroscopic relative density rather than the microstructural parameters obtained in Ref. [11] are more convenient to engineering application. For uniform and regular Plateau porous structure, our results shown in Eqs. (32)-(34) are the same as those in Ref. [11].
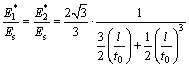 (32)
(32)
 (33)
(33)
 (34)
(34)
In addition, hexagonal cellular model and mechanics model of composite materials are used to predict effective elastic constants of porous materials in Refs. [9] and [15], respectively. Let k=1.2 and μ=1/3 for comparison of our models with the other two models.
Calculation formulas of the effective elastic constants were given in Ref. [9] as follows:

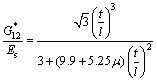

Calculation formula of the effective elastic modulus was given in Ref. [15] as follows:

Figures 6-8 show variation curves of the effective elastic constants with the relative density (ρ*/ρs) obtained in this study, Refs. [9] and [15]. Our results of  and
and  increase with the increase of ρ*/ρs. The larger the relative density, the more the solid material per unit volume, and thus the stronger the resistant ability of the porous material to elastic deformation. When ρ*/ρs is equal to 0 and 1, corresponding to the full air (no solid material) and fully dense material, the Poisson ratio
increase with the increase of ρ*/ρs. The larger the relative density, the more the solid material per unit volume, and thus the stronger the resistant ability of the porous material to elastic deformation. When ρ*/ρs is equal to 0 and 1, corresponding to the full air (no solid material) and fully dense material, the Poisson ratio  is equal to 1 and 0.3-0.5, which results in the decrease of
is equal to 1 and 0.3-0.5, which results in the decrease of  with the increase of ρ*/ρs and the tendency to the Poisson ratio of the dense material. The variations of
with the increase of ρ*/ρs and the tendency to the Poisson ratio of the dense material. The variations of  ,
,  and
and  with ρ*/ρs are consistent with those predicted by Refs. [9] and [15], and also fit well with the actual situation.
with ρ*/ρs are consistent with those predicted by Refs. [9] and [15], and also fit well with the actual situation.

Fig. 6 Variation of  /Es with ρ*/ρs
/Es with ρ*/ρs

Fig. 7 Variation of G*12/Es with ρ*/ρs

Fig. 8 Variation of  with ρ*/ρs
with ρ*/ρs
Compared with the results in Ref. [9], our results of  ,
,  and
and  are almost the same in the low range of ρ*/ρs. and slightly lower in the medium range of ρ*/ρs and more secure. Effects of axial force, shear force and bending moment on the deformation of Plateau porous structure are taken into account for calculating the effective elastic constants both in Ref. [9] and this study. Geometric method is used in Ref. [9] while energy method is used in our study for calculating the displacement. Obviously, our results are more simple and accurate.
are almost the same in the low range of ρ*/ρs. and slightly lower in the medium range of ρ*/ρs and more secure. Effects of axial force, shear force and bending moment on the deformation of Plateau porous structure are taken into account for calculating the effective elastic constants both in Ref. [9] and this study. Geometric method is used in Ref. [9] while energy method is used in our study for calculating the displacement. Obviously, our results are more simple and accurate.
Compared with the results in Ref. [15], our result of  is in good agreement with result in Ref. [15] in the low range of ρ*/ρs, but much lower in the medium and high range of ρ*/ρs. That is because mechanics of composite materials is adopted in Ref. [15], where the porous material is regarded as formation of pore and dense body, and the pore’s elastic modulus is zero. In nature, effect of the pore distribution and pore interaction on weakening of the elastic modulus of Plateau porous structure cannot be considered, resulting in much higher result of
is in good agreement with result in Ref. [15] in the low range of ρ*/ρs, but much lower in the medium and high range of ρ*/ρs. That is because mechanics of composite materials is adopted in Ref. [15], where the porous material is regarded as formation of pore and dense body, and the pore’s elastic modulus is zero. In nature, effect of the pore distribution and pore interaction on weakening of the elastic modulus of Plateau porous structure cannot be considered, resulting in much higher result of  . Therefore, Plateau porous structure model established in this study is more reasonable for characterizing the porous material of medium density and more accurate and reliable for predicting its elastic modulus than the composite materials mechanics model.
. Therefore, Plateau porous structure model established in this study is more reasonable for characterizing the porous material of medium density and more accurate and reliable for predicting its elastic modulus than the composite materials mechanics model.
5 Conclusions
1) A micromechanics model of Plateau porous structure for the new Ti-Al intermetallic compound porous material is established based on microstructure analysis. This model can effectively characterize the open skeleton microstructure and non-uniformity of this new porous material.
2) Calculation formulas of elastic constants (including effective elastic modulus, effective shear elastic modulus and effective Poisson ratio) are derived by the energy method. Results show that both the effective elastic modulus and effective shear elastic modulus increase with the increase of the relative density while the effective Poisson ratio decreases.
3) The explicit expressions of effective elastic constants in terms of the macroscopic relative density obtained in this study are more convenient to engineering application than those in terms of the microstructural parameters obtained in reference.
4) Compared with the currently-existing hexagonal honeycomb model and mechanics model of composite materials, the micromechanics model of heterogeneous Plateau porous structure can take into account the non-uniformity of the microstructure and the effect of the shear on microstructural displacements. Our results of the effective elastic constants obtained by the energy method rather than the geometric method are more accurate for predicting the effective elastic constants of the medium-density porous materials.
References
[1] LETANT S E, HART B R, VAN BUUREN A W, TERMINELLO L J. Functionalized silicon membranes for selective bio-organism capture [J]. Nature Materials, 2003, 2(6): 391-395.
[2] YAMAGUCHI A, UEJO F, YODA T, UCHIDA T, TANAMURA Y, YAMASHITA T. Self-assembly of a silica-surfactant nanocomposite in a porous alumina membrane [J]. Nature Materials, 2004, 3(5): 337-341.
[3] HERNANDEZ N, SANCHEZ-HERENCIA A J, MORENO R. Forming of nickel compacts by a colloidal filtration route [J]. Acta Materialia, 2005, 53(4): 919-925.
[4] van der BRUGGEN B, VANDECASTEELE C. Distillation vs. membrane filtration: Overview of process evolutions in seawater desalination [J]. Desalination, 2002, 143(3): 207-218.
[5] ARIRIATU L E, EWELIKE N C. A low-cost filtration system for the treatment of wastewaters [J]. Environment Protection Engineering, 2003, 29(2): 17-22.
[6] LIU Pei-sheng. Introduction of porous materials [M]. Beijing: Tsinghua University Press, 2004. (in Chinese)
[7] JIANG Yao. Investigation on Ti-Al intermetallic compound porous material [D]. Changsha: Central South University, 2008. (in Chinese)
[8] LI Ting-ting, PENG Chao-qun, WANG Ri-chu, WANG Xiao-feng, LIU Bing, WANG Zhi-yong. Research progress in porous Fe-Al, Ti-A1 and Ni-A1 intermetallic compound porous materials [J]. The Chinese Journal of Nonferrous Metals, 2011, 21(4): 784-795. (in Chinese)
[9] GIBSON L J, ASHBY M F. Cellular solids: Structure and properties [M]. 2nd ed. Cambridge: Cambridge University Press, 1997.
[10] ZHU H X, MILLS N J, KNOTT J F. An analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells [J]. Journal of the Mechanics and Physics of Solids, 1997, 45(3): 319-343.
[11] CHUANG Cheng-Hsin, HUANG Jong-Shin. Elastic moduli and plastic collapse strength of hexagonal honeycombs with plateau borders [J]. International Journal of Mechanical Sciences, 2002, 44: 1827-1844.
[12] LI K, GAO X L, ROY A K. Micromechanics model for three-dimensional open-cell foams using a tetrakaidecahedral unit cell and Castigliano’s second theorem [J]. Composites Science and Technology, 2003, 63: 1769-1781.
[13] KIM H S, AL-HASSANI S T S. A morphological elastic model of general hexagonal columnar structures [J]. International Journal of Mechanical Sciences, 2001, 43: 1027-1060.
[14] RAMAKRISHNAN N, ARUNACHALAM V S. Effective elastic moduli of porous solids [J]. Journal of Material Science, 1990, 25: 3930-3937.
[15] LU Zi-xing, HUANG Zhu-ping, WANG Ren. The theoretical prediction of compressive Young’s moduli for polyurethane foam plastics [J]. Chinese Journal of Applied Mechanics, 1996, 13(2): 9-12. (in Chinese)
[16] LU Zi-xing, HUANG Zhu-ping, WANG Ren. Determination of effective moduli for foam plastics based on three phase spheroidal model [J]. Chinese Journal of Solid Mechanics, 1996, 17(2): 95-101. (in Chinese)
[17] LONG Yu-qiu, BAO Shi-hua. Structural mechanics I [M]. Beijing: Higher Education Press, 2006. (in Chinese).
新型金属间化合物多孔材料有效弹性常数的理论预测
苏淑兰1, 2 ,饶秋华1,贺跃辉3
1. 中南大学 土木工程学院,长沙 410075;
2. 中南林业科技大学 土木工程与力学学院,长沙 410004;
3. 中南大学 粉末冶金研究院,长沙 410083
摘 要:基于新型Ti-Al金属间化合物多孔材料的微结构特征分析,建立了该材料的Plateau多孔结构细观力学模型,通过能量法推导出该多孔材料有效弹性常数(含有效弹性模量、有效剪切弹性模量、有效泊松比)的理论预测公式。计算结果表明:有效弹性模量和有效剪切弹性模量均随着相对密度的增加而增加,但有效泊松比随着相对密度的增加而减小。与现有的六边形蜂窝模型及复合材料力学模型相比,非均匀Plateau多孔结构细观力学模型更适合于表征中密度多孔材料,更能准确地预测中密度多孔材料的有效弹性常数。现有的非均匀Plateau多孔结构模型仅给出有效弹性常数与微观结构参数之间的关系,而本文模型建立了有效弹性常数与宏观相对密度的显式表达式,更方便工程的实际应用。
关键词:金属间化合物;多孔材料;有效弹性常数;Plateau结构;能量法
(Edited by Hua YANG)
Foundation item: Project (50825102) supported by the National Natural Science Funds for Distinguished Young Scholar, China; Project (2009CB623406) supported by the National Basic Research Program of China
Corresponding author: Qiu-hua RAO; Tel: +86-13787265488; E-mail: raoqh@mail.csu.edu.cn
DOI: 10.1016/S1003-6326(13)62570-4