
J. Cent. South Univ. (2018) 25: 2701-2711
DOI: https://doi.org/10.1007/s11771-018-3947-9
Melting heat transfer with radiative effects and homogeneous– heterogeneous reaction in thermally stratified stagnation flow embedded in porous medium
M. JAVED, M. FAROOQ, S. AHMAD, Aisha ANJUM
Department of Mathematics, Riphah International University, Islamabad 44000, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The present article deals with thermally stratified stagnation-point flow saturated in porous medium on surface of variable thickness along with more convincing and reliable surface condition termed as melting heat transfer. Homogeneous–heterogeneous reaction and radiative effects have been further taken into account to reconnoiterproperties of heat transfer. Melting heat transfer and phenomenon of homogeneous–heterogeneous reaction have engrossed widespread utilization in purification of metals, welding process, electroslag melting, biochemical systems, catalysis and several industrial developments. Suitable transformations are utilized to attain a scheme of ordinary differential equations possessing exceedingly nonlinear nature. Homotopic process is employed to develop convergent solutions of the resulting problem. Discussion regarding velocity, thermal field and concentration distribution for several involved parameters is pivotal part. Graphical behaviors of skin friction coefficient and Nusselt number are also portrayed. Concentration of the reactants is found to depreciate as a result of strength of both heterogeneous and homogeneous reaction parameters. With existence of melting phenomenon, declining attitude of fluid temperature is observed for higher radiation parameter.
Key words: melting heat transfer; porous medium; stagnation point; variable sheet thickness; homogeneous– heterogeneous reaction
Cite this article as: M. JAVED, M. FAROOQ, S. AHMAD, Aisha ANJUM. Melting heat transfer with radiative effects and homogeneous- heterogeneous reaction in thermally stratified stagnation flow embedded in porous medium [J]. Journal of Central South University, 2018, 25(11): 2701–2711. DOI: https://doi.org/10.1007/s11771-018-3947-9.
1 Introduction
Recently flows under the influence of chemical reactions have got mentionable attraction for engineers and scientists. Abundant immersion of homogeneous and heterogeneous reactions has been found in quite a number of chemically reactive processes. Such types of chemical reactions occur in biochemical systems, catalysis, hydrometallurgical industry and combustion. Complex interaction occurs between heterogeneous and homogeneous reactions in fluid bulk and upon catalytic surfaces respectively. Such type of interaction is used for intake and manufacture of reactant species at variable rates. Homogeneous reactions have ability to occur uniformly in the whole given phase, while heterogenous reactions occur in the specified range or inside the boundary of a given segment. MERKIN [1] discussed the properties of homogeneous–heterogeneous reaction for isothermal model in the flow of boundary layer. HAYAT et al [2] scrutinized influence of homogeneous–heterogeneous reaction and melting for the stagnation flow of Jeffrey fluid. Analysis of homogeneous–heterogeneous reaction with convective conditions for the case of nano-fluid flow is given by HAYAT et al [3]. HAYAT et al [4] presented a study on combined effects of Hall current and homogeneous–heterogeneous reaction on peristalsis. KAMESWARAN et al [5] developed analysis on stretching flow along with homogeneous–heterogeneous reaction and nanoparticles. KHAN et al [6] investigated the characteristics of homogeneous–heterogeneous reaction for the flow of Casson fluid. MHD flow besides homogeneous–heterogeneous reaction and melting phenomenon was explained by HAYAT et al [7]. Three- dimensional Burger fluid flow for homogeneous and heterogeneous reaction was assessed by KHAN et al [8]. Features of homogeneous–heterogeneous reaction for the Powell–Eyring fluid flow were explored by HAYAT et al [9]. The flow of micro polar fluid along with homogeneous and heterogeneous reaction saturated in porous medium was effectively analyzed by SHAW et al [10].
Heat transfer analysis through melting phenomenon has extraordinary utilization in industries and technology.
Now, scientists have shown attention to the development of low cost, sustainable and efficient energy storage technologies. Mainly there are three processes which are utilized for energy storage namely sensible heat storage, latent heat storage and storage of chemical heat energy. Latent heat storage method is more economical and efficient among all of these methods. Melting heat transfer has wide usage in industries such as purification of metals, welding and electroslag melting. ADEGBIE et al [11] discussed the stagnation flow of micropolar fluid with heat transfer effects through melting phenomenon. The influence of melting heat transfer on the nanofluid flow towards a stretched sheet was demonstrated by MABOOD et al [12]. KRISHNAMURTHY et al [13] explained the suspended particle effect and melting heat transfer for the flow of nano fluid embedded in porous medium. TIEN et al [14] analyzed the melting impact on forced convection heat transfer. MAHMOUD et al [15] presented a study on micropolar fluid flow with melting heat transfer phenomenon in porous medium. KRISHNAMURTHY et al [16] reported the flow of Williamson nanofluid in porous medium with melting heat transfer effects. HAYAT et al [17] made an effort to describe the MHD flow of the 3rd grade fluid besides melting heat transfer effects. ABEL et al [18] discussed the MHD stagnation flow over stretched sheet with the existence of melting heat transfer. Outcomes of melting heat transfer for viscous nanofluid in dual stratified medium were assessed by FAROOQ et al [19].
No doubt the study on flows in porous medium has acquired high importance in many scientific and engineering applications. Problems regarding transfer of heat in porous medium have tremendous usage in thermal engineering such as extraction of crude oil, ground water pollution, thermal insulation, fluid flow across filtering devices. HUSSANAN et al [20] described the unsteady magneto hydro dynamic flow saturated in porous medium with Newtonian heating. NIRANJAN et al [21] explored magneto convection flow along with radiation, homogeneous–heterogeneous reaction and slip effects in porous medium. Stagnation flow of nanofluid with effects of thermal radiations in porous medium was studied by REDDY et al [22]. RAHMAN et al [23] presented a study on unsteady magneto hydro dynamic nanofluid flow in non- Darcian porous medium.
In fact researchers have found less focused in the exploration of fluid properties with melting heat transfer either with uniform or variably thicked surfaces. In addition, such study up to yet has not been investigated in thermally stratified medium. Our aim here is to deal with thermally stratified stagnation flow embedded in porous medium towards a nonlinearly stretched surface along with more realistic melting heat transfer condition. Homogeneous–heterogeneous reaction and thermal radiation effects are also taken into account to explore characteristics of heat transfer. Utilizing suitable transformations, dimensionless governing problems are obtained and then reached at convergent solutions by the procedure of homotopy analysis (HAM) [24–29]. Behavior of several sundry parameters on velocity, thermal and concentration distributions is sketched and discussed graphically. Explicit description of skin friction coefficient as well as Nusselt number for involved parameters is also a part of this study.
2 Problem formulation
Here we scrutinize stagnation flow of viscous and incompressible fluid on the way to nonlinearly stretched sheet of varying thickness in porous medium (see Figure 1). Melting heat transfer phenomenon is introduced to explore heat transfer properties. Homogeneous–heterogeneous reactions along with radiative effects are taken into consideration for disclosing properties of flow. In present study, we have assumed ambient temperature T∞ to be dominant over the surface temperature Tm. Assumption is made for diffusion coefficients to be same for both species. Following homogeneous–heterogeneous reaction model is selected [1]:
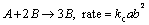
while isothermal as well as catalytic 1st order reaction is represented as follows,

Concentration levels of both of the chemical species A and B are represented by a and b respectively. kc and ks denote rate constants.
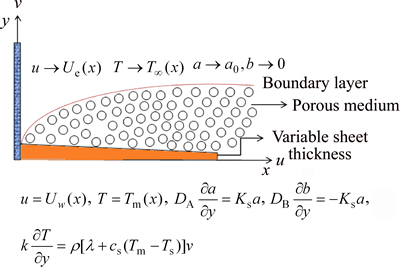
Figure 1 Physical geometry of considered problem
Applying boundary layer approximations to the considered flow analysis yields governing equations of the form,
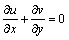 (1)
(1)
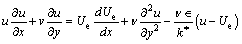 (2)
(2)
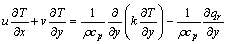 (3)
(3)
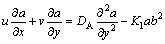 (4)
(4)
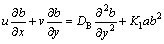 (5)
(5)
we simplify qr the heat flux for radiation by making use of famous Rosseland approximation [30] as,
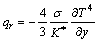
where σ represents Stefan-Boltzmann constant; while K* denotes coefficient of mean absorption. It is important to mention here that T4 is represented as linear temperature function and further it is extended by employing expansion for Taylor series. We obtain following form after ignoring higher order terms,
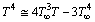
We have interpreted Eq. (3) in abridged form as,
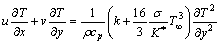 (6)
(6)
Associated conditions for boundary are inscribed below,
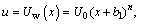
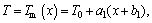
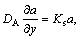
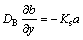
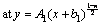 (7)
(7)
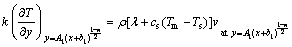 (8)
(8)
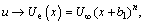
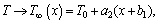
 (9)
(9)
The aforementioned expressions designate u and v the x and y components of velocity, respectively; Uw is stretched velocity; Ue is free stream velocity; λ is latent heat; A1 represents dimensional constant; U0 and U∞ are the velocities for reference; n is the power index for velocity; v is the fluid kinematic viscosity; cp is specific heat capability; ρ the fluid density; DA and DB are coefficients of diffusion species A and B respectively; k depicts thermal conductivity; a0, a1 and a2 are dimensional constants; Ks is strengthening capability of heterogeneous reaction parameter; T is fluid temperature; Tm represents melting surface temperature; T∞ expresses ambient temperature; Ts is solid surface temperature; k* and  denote permeability and porosity of medium respectively.
denote permeability and porosity of medium respectively.
By making use of

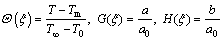 (10)
(10)
the condition (1) gets satisfied in identical manner while Eqs. (2)–(5) adopt below mentioned form,
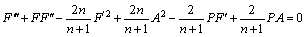 (11)
(11)
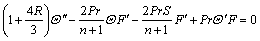 (12)
(12)
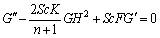 (13)
(13)
 (14)
(14)
depending upon the boundary conditions,
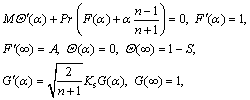
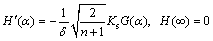 (15)
(15)
where prime represents differentiation in respect of ξ and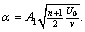 Let
Let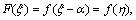
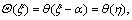
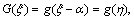 H(ξ)=
H(ξ)= 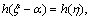 we have,
we have,
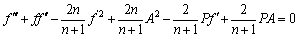 (16)
(16)
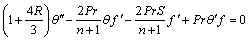 (17)
(17)
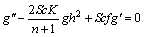 (18)
(18)
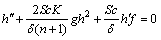 (19)
(19)
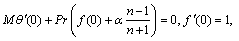
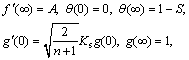
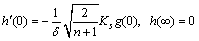 (20)
(20)
where δ shows the ratio of mass diffusion coefficients; Pr is Prandtl number; A represents the velocities ratio; P is the porosity parameter; R denotes radiative parameter; K is strengthening capability of homogeneous reaction parameter while Ks denotes the same for heterogeneous reaction parameter; S is the thermal stratification parameter; Sc is Schmidt number; M is the melting parameter and α represents wall thickness parameter. All of the above mentioned quantities are expressed mathematically as follows,
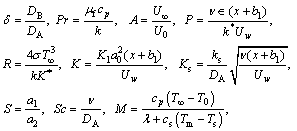
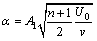 (21)
(21)
where it is worth mentioning that M involves Stefan numbers 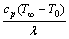 and
and  of the respective liquefied and solid phases. There is a clear indication of the absence of melting phenomenon for M=0. The diffusive coefficients for the previously mentioned chemical species A and B are presumed to possess similar size. Using this point of view, we take DA and DB (diffusion coefficients) to be equal, i.e. δ=1 [7]. Thus,
of the respective liquefied and solid phases. There is a clear indication of the absence of melting phenomenon for M=0. The diffusive coefficients for the previously mentioned chemical species A and B are presumed to possess similar size. Using this point of view, we take DA and DB (diffusion coefficients) to be equal, i.e. δ=1 [7]. Thus,
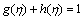 (22)
(22)
Through Eqs. (18) and (19), it implies,
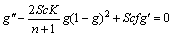 (23)
(23)
with

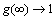 when
when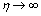
 (24)
(24)
Mathematical portrayal of skin friction coefficient and local Nusselt number is given below,
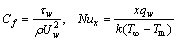
where shear stress τw for wall as well as the heat flux qw is interpreted as follows,
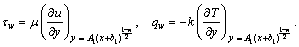
Dimensionless forms of these quantities are
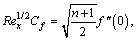
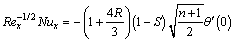 (25)
(25)
In above expression, 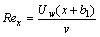 represents local Reynolds number.
represents local Reynolds number.
3 Homotopic solutions
In the recent past homotopic procedure (HAM) has been executed by several researchers to obtain solutions of several problems particularly of nonlinear nature. In this method there exists great freedom for the choice of starting prediction (i.e., initial guess) besides linear operator to attain the approximate results of problem under consideration. Here relevant base functions and auxiliary operators (linear) are carefully selected as follows,
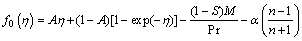 (26)
(26)
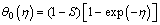 (27)
(27)
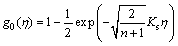 (28)
(28)
The satisfied auxiliary linear operators are,
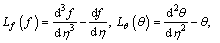
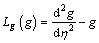 (29)
(29)
along with properties
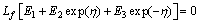 (30)
(30)
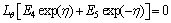 (31)
(31)
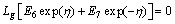 (32)
(32)
where Ei (i=1–7) represent arbitrary constants. Next we have.
3.1 Zeroth-order problems
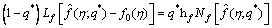 (33)
(33)
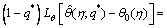
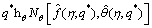 (34)
(34)

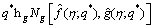 (35)
(35)
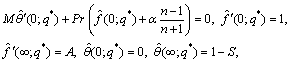
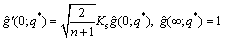 (36)
(36)
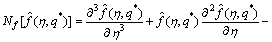
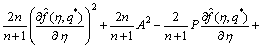
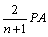 (37)
(37)
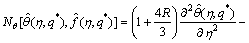
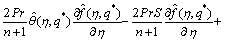
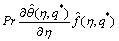 (38)
(38)
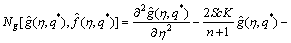

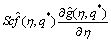 (39)
(39)
where q*symbolizes embedding parameter while 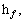
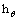 and
and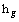 are auxiliary parameters (nonzero);
are auxiliary parameters (nonzero); 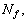 Nθ and Ng specify the nonlinear operators.
Nθ and Ng specify the nonlinear operators.
3.2 m-th order problems
The deformation problems of m-th order are interpreted by,
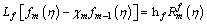 (40)
(40)
 (41)
(41)
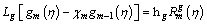 (42)
(42)
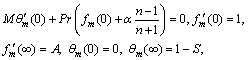
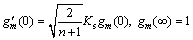 (43)
(43)

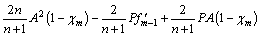 (44)
(44)

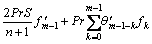 (45)
(45)
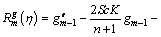
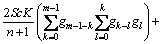
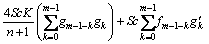 (46)
(46)
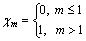 (47)
(47)
For q*=0 and q*=1, we have,
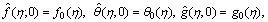
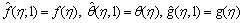 (48)
(48)
f(η, q*), θ(η, q*) and g(η, q*) vary from starting solutions f0(η), θ0(η) and g0(η) to concluding solutions f(η), θ(η) and g(η) when q* fluctuates from 0 to 1. Applying Taylor’s series expansion gives,
 (49)
(49)
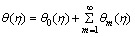 (50)
(50)
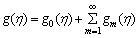 (51)
(51)
Resulting ultimate solutions (fm, θm and gm) in the form of distinctive (special) solutions 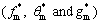 are construed as follows:
are construed as follows:
 (52)
(52)
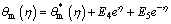 (53)
(53)
 (54)
(54)
By making use of boundary conditions, we have,
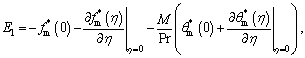

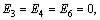

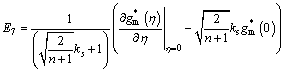 (55)
(55)
3.3 Convergence analysis
No doubt it is fact that homotopy analysis method can be utilized efficiently to manage and regulate the converging behavior of series solutions. In this regard there is a vital role of auxiliary parameters 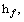
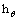 and
and 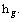 In this study
In this study 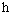 -curves are sketched (see Figure 2). Allowable values of auxiliary parameters exist in the ranges,
-curves are sketched (see Figure 2). Allowable values of auxiliary parameters exist in the ranges, 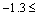
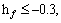
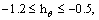
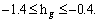
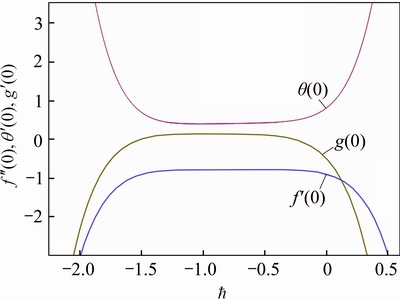
Figure 2  curves for f ″(0), θ′(0) and g′(0) when R=0.2, M=0.6, Pr=1.2, n=1, Sc=1.2, K1=0.3, Ks=1, P=0.1, A=0.1 and S=0.2
curves for f ″(0), θ′(0) and g′(0) when R=0.2, M=0.6, Pr=1.2, n=1, Sc=1.2, K1=0.3, Ks=1, P=0.1, A=0.1 and S=0.2
4 Discussion
Features of different arising parameters are analyzed on velocity, thermal and concentration distributions in this section. Figure 3 demonstrates the influence of wall thickness parameter α on the profile for velocity f ′(η). It is assessed graphically that upon increasing value of α, there is decline in velocity. Boundary layer thickness for velocity also shows declining attitude as a result of growth in α. Stretching velocity reduces increment in α due to which velocity of the fluid decreases. While in Figure 4 impact of power index n upon velocity distribution f ′(η) is sketched. Velocity profile decreases and similarly associated momentum boundary layer thickness gets thinner for increase in value of power index n. In the presence of melting phenomenon, decrement in velocity profile f ′(η) is seen upon increment in porosity parameter P which is evident from Figure 5. It is physically justified due to the fact that as porosity parameter P enhances, it reduces the rate of permeability which ultimately causes to decrease velocity distribution. While Figure 6 displays the impression of the melting parameter M for f ′(η). Upon increasing value of melting parameter M an increment is observed in the velocity f ′(η). Due to developed melting rate, more heat gets transferred from the hotter fluid in the direction of surface which results in greater convective flow. Consequently, velocity distribution enhances. Impact of the radiative parameter R on thermal field θ(η) is analyzed in Figure 7. Temperature profile decays increasing of the radiative parameter R. It is physically justified because of the fact that increasing radiation parameter R refers decrement in rate of mean absorption coefficient. Consequently, temperature of fluid falls down. Stratification effect on thermal field θ(η) is portrayed in Figure 8. Clearly temperature deteriorates as a result of rise in the value of stratification parameter S. As stratification parameter S enhances, it relates to higher melting surface temperature which is the reason for reduced temperature of fluid. While thermal boundary layer is observed to be thicker for higher stratification parameter S. We see in Figure 9 that thermal profile θ(η) increases for enhancement of Prandtl number Pr, while thermal boundary layer thickness decreases in this case. Prandtl number is normally explained as the ratio of momentum and thermal diffusivity. Increment in Pr is associated with lesser thermal diffusivity due to which small amount of heat gets off towards the melting surface. That ultimately rises thermal field. Figure 10 displays the impression of melting parameter M on distribution for temperature θ(η). It is observed that as we increase the value of M, temperature gets off from the system. On the other hand, increment in the value of M leads to thicker thermal boundary layer. It is worth mentioning that for greater value of M more heat gets transferred from the fluid towards surface which causes reduction in temperature. Impact of strengthening capacity of heterogeneous parameter Ks upon profile for concentration g(η) is displayed in Figure 11. Concentration profile gets declined upon increment in the value of Ks. Behavior of Schmidt number Sc on g(η) concentration field is sketched in Figure 12. Upon increment in the value of Sc, the concentration distribution g(η) grows up. Momentum and mass diffusivity ratio is termed as Schmidt number. Increment in Schmidt number is associated with small mass diffusivity due to which concentration enhances. The impact of strengthening capacity of homogeneous reaction parameter K on concentration profile g(η) is depicted in Figure 13. Concentration distribution shows recessive attitude while associated solutal boundary layer thickness behaves in opposite manner for higher values of K. In Figure 14 the impact of porosity parameter P and ratio velocity parameter A on skin friction coefficient Cf is interpreted. Enhancement of Cf is explored for greater values of A and P. Effect of radiative parameter R and thermal stratification parameter S on Nusselt number is demonstrated in Figure 15. An increasing behavior is noted for Nusselt number as a result of increment in the values of both R and S.
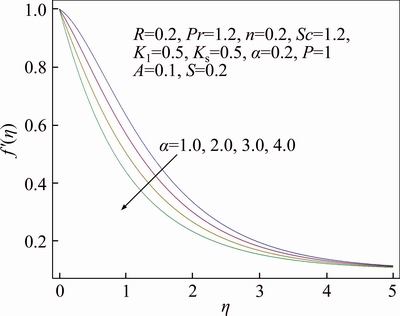
Figure 3 Behavior of α in respect of f′
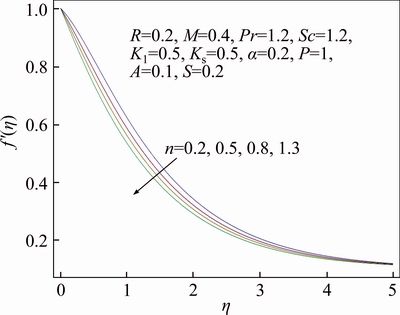
Figure 4 Behavior of n in respect of f′
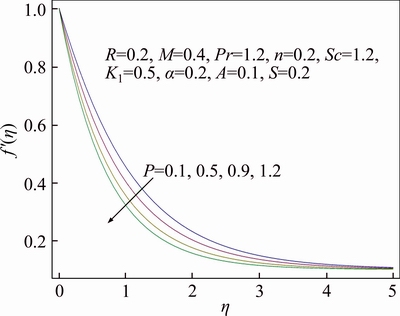
Figure 5 Behavior of P in respect of f′
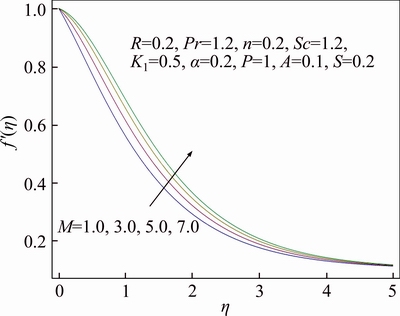
Figure 6 Behavior of M in respect of f′
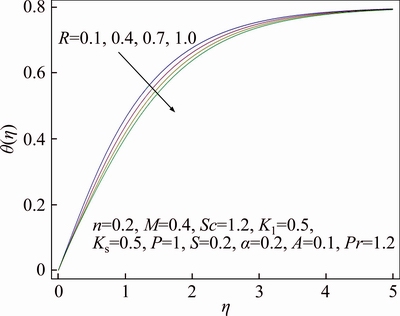
Figure 7 Behavior of R in respect of θ
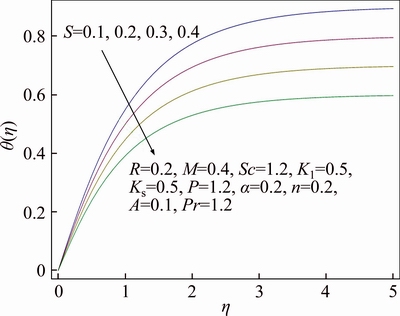
Figure 8 Behavior of S in respect of θ
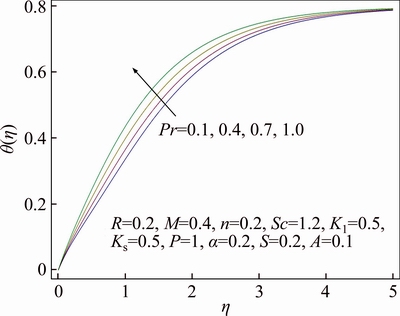
Figure 9 Behavior of Pr in respect of θ
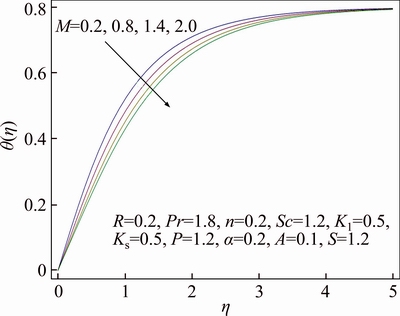
Figure 10 Behavior of M in respect of θ
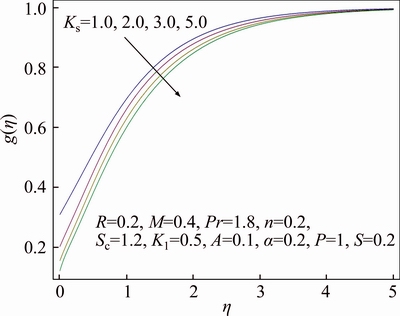
Figure 11 Behavior of Ks in respect of g

Figure 12 Behavior of Sc in respect of g

Figure 13 Behavior of K in respect of g
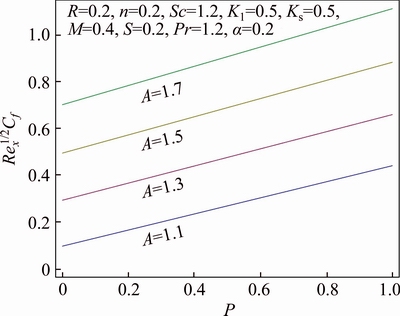
Figure 14 Behavior of Cf in respect of A and P

Figure 15 Behavior of Nu in respect of S and R
5 Conclusions
We have inspected heat transfer features via melting phenomenon for stagnation flow along with homogeneous–heterogeneous reaction and radiative effects embedded in porous medium. Concluding remarks are summarized as follows:
1) Decrement in velocity profile is evident for stronger wall thickness parameter.
2) Concentration profile depreciates as a result of strengthening capacity of homogeneous reaction parameter.
3) Increment in Schmidt number gives rise to enriched field for concentration.
4) Concentration field for the reactant species declines for the sturdier values of heterogeneous reaction parameter.
5) Enhancement of radiative parameter gives declining attitude of temperature profile.
References
[1] MERKIN J H. A model for isothermal homogeneous- heterogeneous reactions inboundary-layer flow [J]. Math Computer Model, 1996, 24: 125–136.
[2] HAYAT T, FAROOQ M, ALSAEDI A. Characteristics of homogeneous-heterogeneous reactionsand melting heat transfer in the stagnation point flow of Jeffrey fluid [J]. J Appl Fluid Mech, 2016, 9: 809–816.
[3] HAYAT T, HUSSAIN Z, ALSAEDI A, ASGHAR S. Carbon nanotubes effects in the stagnation pointflow towards a nonlinear stretching sheet with variable thickness [J]. Adv Powder Tech, 2016, 27: 1677–1688.
[4] HAYAT T, BIBI A, YASMIN H, AHMAD B. Simultaneous effects of Hall current and homogeneous/heterogeneous reactions on peristalsis [J]. J Taiwan Inst Chem Eng, 2016, 58: 28–38.
[5] KAMESWARAN P K, SHAW S, SIBANDA P, MURTHY P V S N. Homogeneous-heterogeneous reactions in a nanofluid flow due to a porous stretching sheet [J]. Int J Heat Mass Transfer, 2013, 57: 465–472.
[6] KHAN M I, WAQAS M, HAYAT T, ALSAEDI A. A comparative study of Casson fluid with homogeneous- heterogeneous reactions [J]. Journal of Colloid & Interface Science, 2017, 498: 85–90.
[7] HAYAT T, KHAN M I, ALSAEDI A, KHAN M I. Homogeneous-heterogeneous reactions and melting heat transfer effects in the MHD flow by a stretching surface withvariable thickness [J]. J Mol Liq, 2016, 223: 960–968.
[8] KHAN W A, ALSHOMRANI A S, KHAN M. Assessment on characteristics of heterogeneous-homogenous processes in three-dimensional flow of Burgers fluid [J]. Res in Physics, 2016, 6: 772–779.
[9] HAYAT T, IMTIAZ M, ALSAEDI A. Effects of homogeneous-heterogeneous reactions inflow of Powell-Eyring fluid [J]. J Cent South Univ, 2015, 22: 3211–3216.
[10] SHAW S, KAMESWARAN P K, SIBANDA P. Homogeneous-heterogeneous reactions in micropolar fluid flow from a permeable stretching or shrinking sheet in a porous medium [J]. Bound Val Problems, 2013, 2013: 77.
[11] ADEGBIE S K, KORIKO O K, ANIMASAUN I L. Melting heat transfer effects on stagnation point flow of micropolar fluid with variable dynamic viscosity and thermal conductivity at constant vortex viscosity [J]. J Nig Math Soc, 2016, 35: 34–47.
[12] MABOOD F, DAS K. Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip [J]. Eur Phys J Plus, 2016, 3: 131–138.
[13] KRISHNAMURTHY M R, GIREESHA B J, GORLA R S R, PRASANNAKUMARA B C. Suspended particle effect on slip flow and melting heat transfer of nanofluid over a stretching sheet embedded in a porous medium in the presence of nonlinear thermal radiation [J]. J Nanofluids, 2016, 5: 502–510.
[14] TIEN C, CHAO Y. The effect of melting on forced convection heat transfer [J]. J App Met, 1965, 4: 523–527.
[15] MAHMOUD M A A, WAHEED S E. Melting heat transfer effects on stagnation point flow of micropolar fluid saturated in porous medium with internal heat generation (absorption) [J]. App Math Mech, 2014, 35: 979–992.
[16] KRISHNAMURTHY M R, PRASANNAKUMARA B C, GIREESHA B J, GORLA R S R. Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium [J]. Eng Sci and Tech Int J, 2016, 19: 53–61.
[17] HAYAT T, IMTIAZ M, ALSAEDI A. Melting heat transfer in the MHD flow of Cu-water nanofluid with viscous dissipation and Joule heating [J]. Adv Powder Tech, 2016, 27: 1301–1308.
[18] ABEL M S, SANAMANI J. Melting heat transfer in MHD boundary layer stagnation pointflow towards a stretching sheet [J]. IOSR J Math, 2015, 11: 91–98.
[19] FAROOQ M, JAVED M, KHAN M I, ANJUM A, HAYAT T. Melting heat transfer and double stratification in stagnation flow of viscous nanofluid [J]. Res in Physics, 2017, 7: 2296–2301.
[20] HUSSANAN A, ISMAIL Z, KHAN I, HUSSEIN A G, SHAFIE S. Unsteady boundary layer MHD free convection flow in a porous medium with constant mass diffusion and Newtonian heating [J]. Eur Phys J Plus, 2014, 129: 46.
[21] NIRANJAN H, SIVASANKARAN S, BHUVANESWARI M. Analytical and numerical study on magneto convection stagnation point flow in a porous medium with chemical reaction, radiation and slip effects [J]. Math Prob Eng, 2016, 10: 1–12.
[22] REDDY M G, PADMA P, SHANKAR B, GIREESHA B J. Thermal radiation effects on MHD stagnation point flow of nanofluid over a stretching sheet in a porous medium [J]. J Nanofluids, 2016, 5: 753–764.
[23] RAHMAN A, GAMAL M. Unsteady magneto hydrodynamic flow of a non-Newtonian nanofluid with thermal radiation effects in non-Darcian porous medium over stretching surface [J]. J Nanofluids, 2016, 5: 721–727.
[24] CAO Ren-yi, CHEN Ling, ZEE MA Y, LIU Xue-ying, YU Bai-hui. Characteristics of unsteady flow in porous media while considering threshold pressure gradient with Green’s function [J]. Journal of Central South University, 2016, 23(1): 201-208. DOI: 10.1007/s11771-016-3063-7.
[25] JIANG Yuan-yong, XU Zeng-he, ZHANG Meng-zhou, BAI Li-yuan. Interactions between gas flow and reversible chemical reaction in porous media [J]. Journal of Central South University, 2017, 24(5): 1144-1154. DOI: 10.1007/ s11771-017-3517-6.
[26] ZHU J, YANG D, ZHENG L, ZHANG X. Effects of second order velocity slip and nanoparticles migration on flow of Buongiorno nanofluid [J]. Appl Math Letters, 2016, 52: 183–191.
[27] HAYAT T, FAROOQ M, ALSAEDI A. Thermally stratified stagnation point flow of Casson fluid with slip conditions [J]. Int J Numer Method Heat Fluid Flow, 2015, 25: 724–748.
[28] HAYAT T, WAQAS M, KHAN M I, ALSAEDI A, SHEHZAD S A. Magneto hydrodynamic flow of burgers fluid with heat source and power law heat flux [J]. Chi J Phys, 2017, 55: 318–330.
[29] HAYAT T, HUSSAIN S, MUHAMMAD T, ALSAEDI A, AYUB M. Radiative flow of Powell–Eyring nanofluid with convective boundary conditions [J]. Chi J Phys, 2017, 55: 1523–1538.
[30] SPARROW E M, CESS R D. Radiation heat transfer [M]. Washington, DC: Hemisphere Publi Corp, 1978.
(Edited by YANG Hua)
中文导读
多孔介质中热层滞流中辐射效应和均相–非均相反应的熔化传热
摘要:本文研究了不同厚度多孔介质中的饱和热层滞点流的熔化传热。进一步研究了均相–非均相反应和辐射效应对传热性能的影响。熔融传热和均相反应现象在金属纯化、焊接工艺、电渣熔炼、生化系统、催化和工业中得到了广泛应用。利用同伦过程给出了问题的收敛解。讨论了几个相关参数,速度、热场和浓度分布。本文还描述了摩擦系数和Nusselt数的图解。反应物的浓度由于非均相和均相反应参数强度的变化而降低。由于熔融现象的存在,在较高的辐射参数下,流体温度下降。
关键词:熔化传热;多孔介质;停滞点;变厚度;均相–非均相反应
Received date: 2017-09-19; Accepted date: 2018-03-09
Corresponding author: M. JAVED, PhD; Tel: +92-300-5301637; E-mail: mubashar.bstar@yahoo.com; ORCID: 0000-0002-6096-8713