J. Cent. South Univ. (2018) 25: 1475-1488

DOI: https://doi.org/10.1007/s11771-018-3841-5

Optimized algorithm in mine production planning, mined material destination, and ultimate pit limit

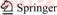
Rahimi ESMAEIL, Moosavi EHSAN, Shirinabadi REZA, Gholinejad MEHRAN

Department of Mining Engineering, Islamic Azad University, South Tehran Branch, Tehran 163963476, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: An integral connection exists among the mine production planning, the mined material destination, and the ultimate pit limit (UPL) in the mining engineering economy. This relation is reinforced by real information and the benefits it engenders in the mining economy. Hence, it is important to create optimizing algorithms to reduce the errors of economic calculations. In this work, a logical mathematical algorithm that considers the important designing parameters and the mining economy is proposed. This algorithm creates an optimizing repetitive process among different designing constituents and directs them into the maximum amount of the mine economical parameters. This process will produce the highest amount of ores and the highest degree of safety. The modeling produces a new relation between the concept of the cutoff grade, mine designing, and mine planning, and it provides the maximum benefit by calculating the destination of the ores. The proposed algorithm is evaluated in a real case study. The results show that the net present value of the mine production is increased by 3% compared to previous methods of production design and UPL.

Key words: mined material destination; ultimate pit limit; net present value; production planning

Cite this article as: Rahimi ESMAEIL, Moosavi EHSAN, Shirinabadi REZA, Gholinejad MEHRAN. Optimized algorithm in mine production planning, mined material destination, and ultimate pit limit [J]. Journal of Central South University, 2018, 25(6): 1475–1488. DOI: https://doi.org/10.1007/s11771-018-3841-5.

1 Introduction

Over the last 50 years or so, a wide range of numerical methods for mining science applications has been developed. Today, with the application of geostatistics, three-dimensional (3D) modeling, the Lerchs–Grossmann algorithm, the Lane algorithm, and many other methods based on computer programs, it is possible to create better mining plans. One of the best observations for optimization of the cutoff grade is LANE’s theory [1–3]. This theory leads to the construction of a maximization function of the net present value (NPV) of cash flow; however, it can also include various constraints on the capacities (mine, mill, leach, SX, EW, and refinery) in the mining operation.

Several researchers have conducted studies in this direction, including SHINKUMA et al [4], CAIRNS et al [5], ATAEI et al [6–8], RASHIDINEJAD et al [9, 10], RENDU [11, 12], GHOLAMNEJAD [13, 14], NEWMAN et al [15], GANGULI et al [16], ABDEL et al [17], DIMITRAKOPOULOS [18], JOHNSON et al [19], AZIMI et al [20–22], ABDOLLAHISHARIF et al [23], ASAD et al [24], NIETO et al [25], THOMPSON et al [26], YASREBI et al [27], RAHIMI et al [28–30], AKBARI et al [31], and GOODFELLOW et al [32]. Their methods have assumed the mining sequence to be known in advance. Nevertheless, the mining sequence is influenced by the cutoff grade choice. Therefore, various attempts have been made to develop a computerized procedure for optimization of the cutoff grade with consideration of the mining sequence, such as relying on penalization (Dantzig- Wolf) [33, 34], Lagrangian relaxation [35], the method of DAGDELEN et al [36], the approach of KAWAHATA [37], BOLAND et al’s method [38], the method of MOOSAVI et al [39, 40], four- dimensional network relaxation (AKAIKE et al [41]), MOGI et al’s approach [42], simulated annealing (KUMRAL et al [43, 44]), GODOY et al’s method [45], the approach of ALBOR CONSUEGRA et al [46]), ant colony optimization (SHISHVAN et al [47]), particle swarm optimization (KHAN et al [48]), tabu search (LAMGHARI et al [49]), the method of RAHIMI et al [50], dynamic programming (RAMAZAN [51]), and the method of WANG et al [52]. Unfortunately, none of these attempts has been widely employed.

Meanwhile, the ultimate pit limit (UPL) has been defined from different perspectives throughout the years. HUSTRULID (1995) introduced the pit existing at the end of the mining operation, called the final or ultimate pit. In between the birth and death of an open pit mine, there is a series of intermediate pits. For developing a pit, the destination of the material of differing values within the pit must be assigned with consideration of the economic criteria. Currently, a popular definition of the ultimate pit exists. The ultimate pit is the pit that engenders the highest NPV compared the other potential pits. Historically, the initial economical UPL determination algorithm was that of LERCH et al [53, 54]. They presented a 3D graph method as a methodology for ultimate pit determination by a computer and a block model of the deposit. Meanwhile, ZHAO et al [55] improved the Lerchs–Grossmann algorithm by considering only the arcs defined in the ore-waste interfaces. However, they developed their algorithm regardless of the multi-processing cutoff grade determination. Similar to ZHAO et al [55], in 1995 YAMATOMI et al [56] attempted to improve another concept by modifying the floating cone algorithm. They likewise did not consider the multi-processing cutoff grade determination.

Gradually, the concept of the ultimate pit determination has become more increasingly applied in interactions with production planning and cutoff grades compared to determining an optimum production plan. Hence, mine planner efforts are expected to become focused on providing strong production planning within the forecasted limits of the open pit mine, or determining pit limits while defining mine planning to maximize the operation NPV. Linear programming (LP) methods are suitable types to address these objectives. Some of these methods were presented by GERSHON in 1982 [57], and HUTTAGOSOL et al in 1992 [58], without accounting for the problem of multi-processing cutoff grade determination. Moreover, most of the artificial intelligence techniques that were used in these method types collectively addressed UPL determination, cutoff grade determination, and production planning. The most successful method of this type was presented by TOLWINSKI et al [59] in 1992. In 1987, GERSHON [57] calculated a heuristic method for only production planning, while WANG et al [60] modified it in 1992 for simultaneously determining the UPL and production planning. GERSHON [57] utilized the concept of the block positional weight. WANG et al [60] utilized Gershon’s downward cone concept in their heuristic; however, their approach does not require the ultimate pit to be determined first. The mentioned heuristics suffer from defects in some cases, such as overlapping cones and the inability to optimize the NPV, while neglecting the problem of multi-processing cutoff grade determination, such as the other discussed algorithms.

In this work, the assumed amount of cutoff grade was precisely chosen for UPL production planning and determination in the Lerchs– Grossman algorithm and/or other analytical and numerical methods. Moreover, this assumed amount of cutoff grade was amended and more closely reached the optimum amount to access the greatest possible final benefit from the operation. This innovative algorithm includes three repetitive processes, each one optimizing different parameters by making iteration conditions. This approach is essential to properly selecting the cutoff grade for determining the instant and ultimate limit of the pit. Furthermore, this approach is highly considered for precisely planning the production and design for excavating pushbacks. Such mine production planning becomes more important when there are different destinations for sending ores with different capacities.

For the first step in the above production planning, it is necessary to calculate the cutoff grade and various destinations of ores in order to determine a new pattern of production planning. For the next step, the final mine production should be calculated. Eventually, different planning frames should be made. Since this process can affect the amount of ore tonnage, the exploitable deposit, and the tonnage amount sent to different plants, it can influence the amount of the cutoff grade by means of the proposed algorithm specifying the cutoff grade.

2 Modeling

2.1 Proposed algorithm

In the first step of the proposed algorithm, it is essential to consider the basic assumption of geology and processing for reserving, as well as the cutoff grade and design capacities for the plants (Figure 1). In this step, it is important to note the mineralogy and grade to determine the destination of the ores. The consideration is based on the processing of the parameters of the ores and mineralogy, which is performed in different processing laboratories. Moreover, the first step is conducted by selecting a destination to send the stockpiles, waste, and the ore blocks.

Kinetic factors are defined in the algorithm to change the project life time, optimize the profit, and change the various heap limits to apply the optimizing iteration algorithm. These factors are represented as i, j, and k, respectively. Consequently, the first assumed geological grade is considered and the capacities of production, project life, and profit are calculated by making the profit function or the cash flow. According to the fact that the NPV embraces the optimizing and maximizing criteria, the following relation can be practiced to calculate the NPV from the cash flow. In fact, the cash flow (CF) function and all influential economic factors should be made as below:

                    (1)

In the above relation, is the discount rate; t is the project life indicator; and t₀ and T_life are the beginning and ending time of the plant production, respectively.

The increase of the maximum carefulness is considered the main condition of the consecutive iteration algorithm. In this step, the processes of repeating the optimum amounts of the cutoff grade are finished, and the project life and secondary NPV are calculated. However, these amounts are not the final optimum amounts regarding for production planning and UPL. Hence, the iteration co-efficiency of k is used and the final amounts of the cutoff grade and NPV are calculated. The iteration processes of planning the final product, final pit, and cut-of grade are calculated by sending different ores and the maximum current NPV. For this purpose, various algorithms can be used, of which the Lerchs–Grossman algorithm is the best one. The algorithm type is not very significant in the proposed approach. The algorithm presented herein can independently calculate the final amounts of the above-mentioned parameters.

2.2 Mined material destination

Determining the destination of ores affects not only the benefits of mining activities, but also the mine production planning process. Thus, it is essential to determine the destination. At first, it seems that the cutoff grades are the only indicators for determining the destination. However, more careful analysis clarifies that the geological and mineralogical studies contribute to determining the destinations of most mined copper and all metal ores. Thus, there are defects in all the algorithms that determine the ores regardless of the ore mineralogy. Different methods are applied to specify the cutoff grades of mines. In this work, a multi-variable maximizing method is employed based on mathematical principles and analytical relationships. This method is based on maximizing the NPV. According to relation Eq. (1), it is possible to achieve the target by maximizing the cash flow. The minable ore tonnage σ_Ei, can be calculated as:

(2)

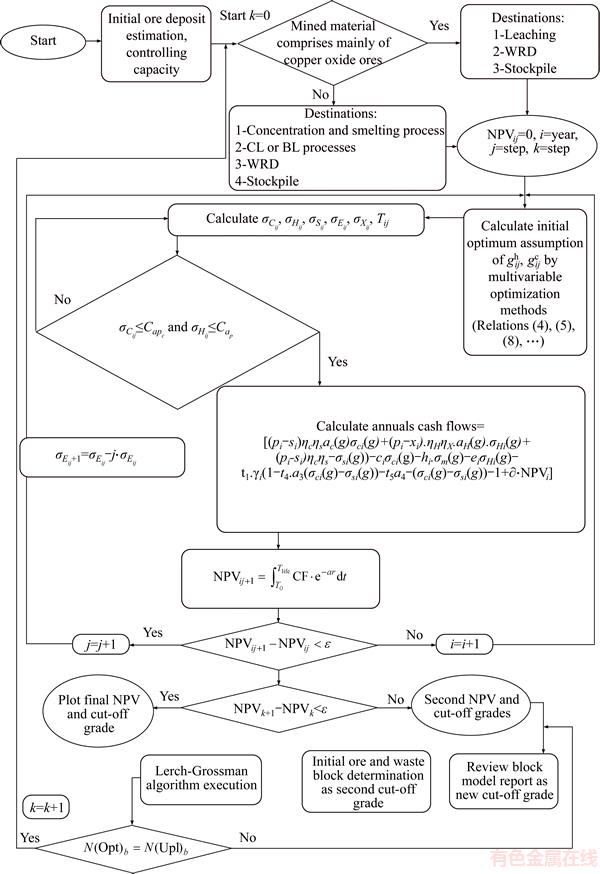
Figure 1 Determining mined material destination, cutoff grades, and UPL of the proposed algorithm

where g_up and g_down respectively show the upper and lower limit of the grade category in the grade- tonnage table. In addition, q is the material tonnage; ζ is the grade category indicator; γ(W, S) denotes the dumped materials; and g^h and g^c are the heap leaching cutoff grade and mill cutoff grades,respectively. The commodities produced by pyrometallurgical and hydrometallurgical plants are calculated as:

                    (3)

                 (4)

where η_c and η_H are the concentration recovery and heap leaching recovery. The above method of determining optimum amounts of variable grades in integrals reveals that the operational limit is the grade limit. The following relations are applied to calculate the optimum amount of the grade amounts.

            (5)

In Eq. (5), f ^c indicates the fixed cost of concentration and smelting methods, and f ^h is the fixed cost of the heap leaching method. In addition, h denotes the operating cost. The two costs of solvent extraction (SX) and electrowinning (EW) are indicated by x_sx and x_ew, respectively. The leaching costs are l; the mining costs are e and the concentration costs are c.

Finally, the optimum cutoff grade is selected between all candidate cutoff grades according to the majority of constraints of the plant capacity. This can be selected based on the different capacities of the plant. The best plant capacity leading to the highest NPV of the process can be selected to determine the limiting capacity. For this purpose, the numerical study of all NPVs should be used. In addition, the maximum amounts should be determined by encryption and trial error.

2.3 UPL and production planning

The best ore is a substance that has the highest grade and lowest waste and must return the amount of material to be extracted. In such circumstances, the central pit has the highest value, which makes it maximized. The cutoff grade is effective on the average grade, UPL, sequence of extraction operations, and tonnage of extractable ore. In each section, there is an optimal pit in which there is an optimal cutoff grade each time that the NPV maximized. Therefore, any algorithm affecting the grade optimization and NPV maximization can be used to specify the most economical pit.

As observed in Figure 1, the proposed algorithm calculates the amount of the optimum pit and cutoff grades by operating the iteration operation in one of the algorithms. Holistically, relation Eq. (5) is assumed, in which the cutoff grades are determined by the proposed algorithm; the NPV amount and optimum pit are determined based on maximizing the value of each block. This NPV is entered into Eq. (1) and the optimizing cutoff grade is once again conducted. Sequentially, the optimum cutoff grades and the maximum NPV and UPL are calculated.

3 Case study

3.1 Reserve description

In this study, a real case study based on a large copper mine with an almost low grade was used to assess the proposed model. The first exploration process of this ore occurred in 1930 and was completed in 1982. The beginning processes of this mineral ore included geo-physical and geo- chemical studies. Figure 2 illustrates the expanded map of the ore in the geo-physical map of this mine. In the exploration operation of the mine, more than 104 km of core drilling, approximately 180 m³ deep exploration trenches, and 11000 m³ of surface exploration trenches were made. The figure shows the distribution map of the boreholes of this ore deposit.

Figure 2 Geo-physical and geo-chemical map of deposit (a) and distribution map of ore deposit boreholes (b)

Approximately 55000 samples were obtained for the mineralogical studies and grade assessment. Other studies were also conducted on the samples, such as ore processing studies, laboratory studies, semi-industrial tests, and process mapping.

3.2 Exploration data

The geological studies indicated that 97% of the deposit of this mine was located in the central block and the remaining 3% was located in the eastern block. The studies also demonstrated that copper oxides were estimated to comprise 2.3% of this mine deposit and the remainder was comprised of primary and secondary sulfides. With respect to the geological views and different geological cutoff grades, the amount of copper deposit and other metals in this mine determined by the JORK indication is shown in Table 1.

The proposed algorithm was used to determine the minable deposit of this mine because this deposit required the determination of optimum cutoff grades, average cutoff grade, and optimum UPL from an operational point of view. Thus, the proposed algorithm was applied to resolve this issue.

3.3 Block modeling

The presented algorithm was first applied in modeling the sampled exploring boreholes, such as those depicted in Figure 3.

The block modeling was performed after modeling the exploration boreholes and the operation of grade flattening and determining the grade ranges. Figure 4 displays the deposit block model of this mine.

Figure 5 presents a view of its blocks obtained in different levels while profiling different sections of this mine in levels containing suitable deposit.

4 Results

The primary modeling was performed and added to the proposed algorithm. It should be noted that existing methods were employed to perform the exploration studies, block model formation, and estimation of the deposit before this step. As shown in Figure 1, these primary amounts were used to calculate their final amounts through performing the proposed optimization algorithm. Thus, the new optimum cutoff grades were calculated for copper deposit, the tonnage amount for sending to different plants, the amount of the final produced cathode, and UPL. The relationship of these grades with the tonnage amount sent from the mine to different plants, as well as the amount of the final product and UPL, were determined by calculating the average cutoff grades of the proposed algorithm.

Regarding the costs and various design parameters in this case study, it was possible to calculate the amount of optimum cutoff grades of processing methods, the tonnage sent to different plants, and the amount of the final production from different plants (Table 2). As observed in Table 2, as the mine life increases, the optimum cutoff grades of the processing methods decrease for the sake of the lost opportunity cost. In addition, the amount of the final NPV and the cash flow are also indicated in the table below.

Table 1 Amount of copper deposit and other metals in case study mine determined by JORK indication

Figure 3 Modeling sampled exploration boreholes

Figure 4 Deposit block model of case study:

Figure 5 Block model section of case study:

4.1 Cutoff grades and ore tonnage

The calculation of the optimum cutoff grades of processing methods contributed resulted in the Table 2 data of distributing the tonnage-processing grades of the mine. The table shows the base cutoff grade (leaching cutoff grade) of processing and the tonnage of the different amounts of ore hold.Figure 6 shows the amount of the mine deposit to the grade of the leaching method. In Figure 7, this amount is cumulative.

Table 2 Results of optimization model execution

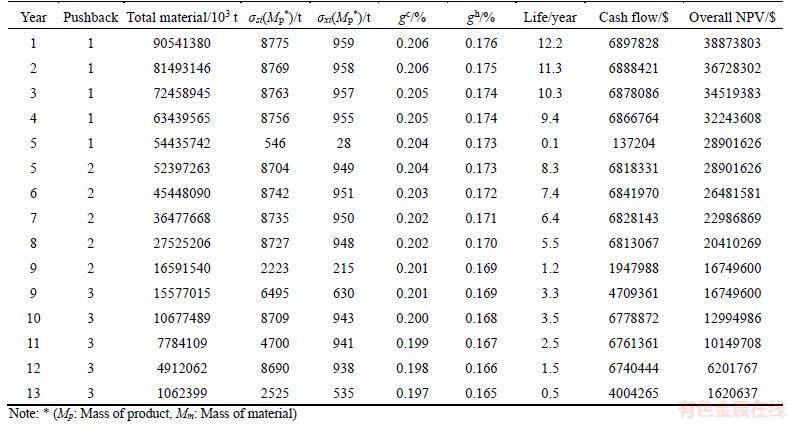
Moreover, the effect of the cutoff grade of the leaching method is presented based on the proposed optimized algorithm. The influence was analyzed based on the amount of the tonnage of the ores extracted from the mine in the case of an optimum pit as well as its indirect effect on the average grade (Figure 8). As observed in Figure 8, if the cutoff grade is 0.2 more than 80×10⁶ t, it is assessed by the average grade of almost 0.3% for the leaching method in the optimum pit.

4.2 Cutoff grades and final products

Figure 9 illustrates the effect of the changes of cutoff grades of the leaching method within different years on the total cathode production of leaching and concentration methods. As expected, the increase of the base cutoff grade of the leaching method reduces the amount of the total cathode production of leaching and concentration methods. However, this reduction is achieved to diminish the economic value of the whole process. In addition, changes are observed in the cathode production curve slope. These changes were caused by different limiting capacities (heap capacity, concentration plant, melting, etc.) in the process of determining the optimum cutoff grades and optimum pit. The calculations by the proposed algorithm of these optimum cathode production values are listed in Table 2.

4.3 Cutoff grades and stripping ratio

Owing to the proposed method optimization process by the innovated algorithm, the amount of the optimum cutoff grades determined by the optimum pit iteration algorithm is presented in Figure 10. The algorithm specifies the most optimized pit regarding the optimum cutoff grades of some processing methods. It is thereby possible to determine the stripping ratio based on the optimum cutoff grades of the processing methods. As shown in the figure, changes in the base optimum cutoff grade of leaching method can be used to assess the stripping ratio based on the optimization algorithm. These changes lead to alterations in cutoff grade concentrations. Therefore, the performance of the optimization algorithm can enable calculation of the amount of the optimum cutoff grades and the optimum pit. Hence, the stripping ratio can also be calculated.

4.4 UPL

The optimum cutoff grades of the processing method were hence determined by the proposed algorithm. Accordingly, the final model of the sample pit with some sections is shown in Figures 11 and 12.

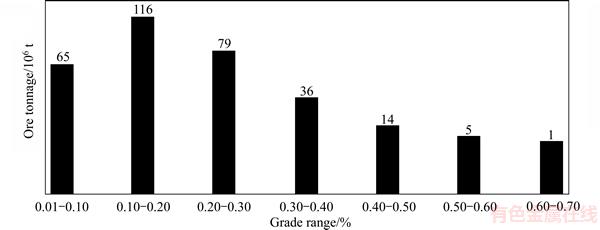
Figure 6 Amount of case study deposit according to grade of leaching method

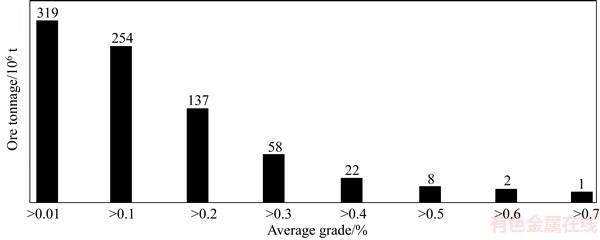
Figure 7 Cumulative amount of deposit according to grade of leaching method

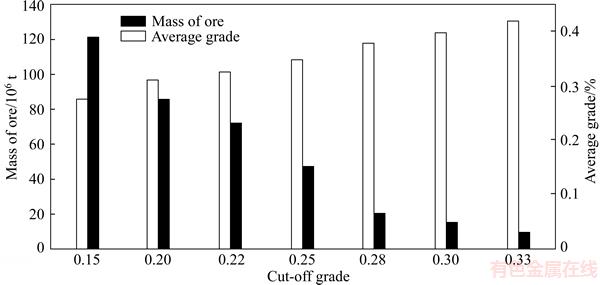
Figure 8 Effect of cutoff grades variation on ore tonnage and average grade in novel algorithm

With consideration of the possibility of using small oxide deposits for the leaching processes, the smaller pit was cost-effectively used and its ores were sent to the leaching plant (Figure 13). In fact, the designation of the plant should have been closer to the smaller pit owing to the optimization of the material transportation direction.

4.5 Copper price, cutoff grade, and internal rate of return

Owing to the influence of the proposed algorithm on optimizing the cutoff grades, the production planning of the mine, and using an economical pit, the effect of copper prices on theses parameters should be evaluated. Regarding the determination of the optimum deposit and the estimated costs of investment and production, the amount of the economical indication of the plan was assessed. In accordance with changes in the copper price, the economical indication of this mine was measured at the most optimum design condition and in different cutoff grades of the leaching method (Figure 14).

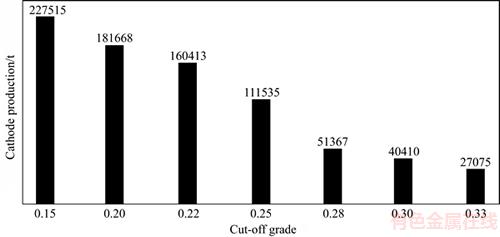
Figure 9 Effect of the changes of cutoff grades of the leaching method in different years on the total cathode production of leaching and concentration methods

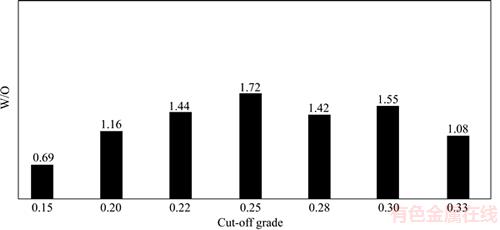
Figure 10 Variation of amount of stripping ratio W/O (waste to ore) by optimum cutoff grades of processing methods

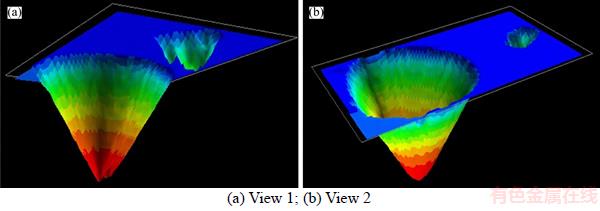
Figure 11 Final model of case study pit based on proposed algorithm and modified processing cutoff grades:

As observed in Figure 14, the increase of the cathode copper enhances the amount of IRR in various cutoff grades of the leaching method. In the case of the cutoff grade of 0.15, the maximum IRR is obtained. On the other hand, the increasing trend of IRR is more than other grades in the case of the cutoff grade of 0.15. This is because there is more metal content in the low cutoff grades.

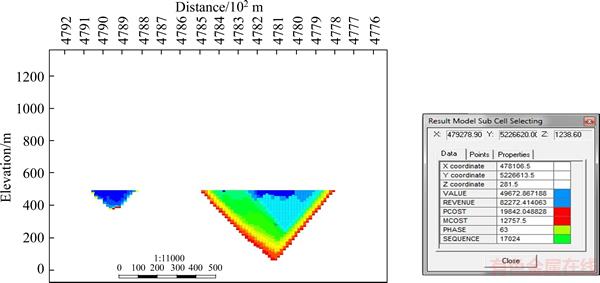
Figure 12 Section of final pit

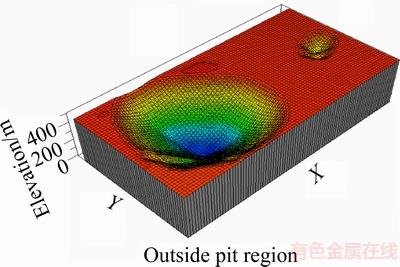
Figure 13 New oxide pit as result of applying proposed optimization algorithm

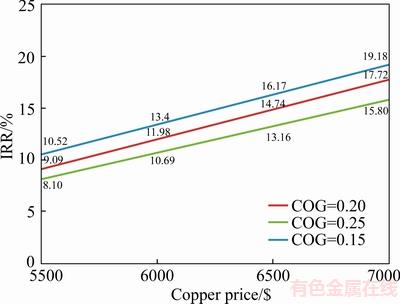
Figure 14 Copper price changes on internal rate of return (IRR) of this mine in different cutoff grades (COG) of leaching method

5 Conclusions

The optimum cutoff grades of processing methods affect not only the destination of the ores, but also the planning of mine production. The results of this study reveal that an algorithm that calculates the amount of the optimum cutoff grades of the mines of several processing plants should be directed at the most economical pit and the most feasible actual planning. The results imply that the proposed algorithm determines the cutoff grade and identifies the roles of all processing methods in the mines based on their cutoff grades. It additionally enhances the total tonnage amount of the materials sent to the plants. Therefore, these new parameters are considered for mine design. Furthermore, the algorithm results indicate that processing the optimum pit for oxide ores would be more beneficial by using hydrometallurgical methods and part of the pit should be devoted to copper production of the ore. It is furthermore demonstrated that the increase in the commodity price of the final product not only decreases the cutoff grades of the hydrometallurgy methods, but also optimizes the economical production. The study findings also indicate that the use of the proposed algorithm to determine the cutoff grade is more effective on the stripping ratio obtained and the amount of the final product.

Acknowledgments

The authors are grateful to Golgohar Company for providing related information. We are also grateful to Mrs. Azarme for her assistance in editing this paper.

References

[1] LANE K F. Choosing the optimum cut-off grade [J]. Quarterly of the Colorado School of Mines, 1964, 59: 811–829.

[2] LANE K F. Cut-off grades for two minerals [C]// Proceedings of the 18th International Symposium on the Application of Computers and Operations Research in the Minerals Industries (APCOM1984). London, 1984: 485–492.

[3] LANE K F. The economic definition of ore: Cut-off grades in theory and practice [M]// Mining Journal Books (ISBN: 0 900117 45 1). London, UK, 1988.

[4] SHINKUMA T, NISHIYAMA T. The grade selection rule of the metal mines: An empirical study on copper mines [J]. Resources Policy, 2000, 26: 31–38.

[5] CAIRNS R D, SHINKUMA T. The choice of cutoff grade in mining [J]. Resource Policy, 2003, 29: 75–81.

[6] ATAEI M, OSANLOO M. Determination of optimum cut-off grades of multiple metal deposits by using the golden section search method [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2003, 103(8): 493–499.

[7] ATAEI M, OSANLOO M. Methods for calculation of optimal cut-off grades in complex ore deposits [J]. Journal of Mining Science, 2003, 39(5): 499–507.

[8] ATAEI M, OSANLOO M. Using a combination of genetic algorithm and the grid search method to determine optimum cut-off grades of multiple metal deposits [J]. International Journal of Surface Mining, Reclamation and Environment, 2004, 18(1): 60–78.

[9] RASHIDINEJAD F, OSANLOO M, REZAI B. Cut off grades optimization with environmental management: A case study: Sungun copper project, IUST [J]. Int J Eng Sci, 2008, 19: 1–13.

[10] RASHIDINEJAD F, OSANLOO M, REZAI B. An environmental oriented model for optimum cut-off grades in open pit mining projects to minimize acid mine drainage [J]. Int J Environ Sci Tech, 2008, 5(2): 183–194.

[11] RENDU J M. An introduction to cutoff grade estimation [M]. Littleton: The Society for Mining, Metallurgy and Exploration Inc, 2008.

[12] RENDU J M. Cut-off grade estimation–old principles revisited–Application to optimisation of net present value and internal rate of return, orebody modelling and strategic mine planning [M]. Perth, 2009: 165–169.

[13] GHOLAMNEJAD J. Determination of the optimum cut-off grade considering environmental cost [J]. Journal of International Environmental Application and Science, 2008, 3(3): 186–194.

[14] GHOLAMNEJAD J. Incorporation of rehabilitation cost into the optimum cut-off grade determination [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2009, 108(2): 89–94.

[15] NEWMAN A, RUBIO N, CARO R, WEINTRAUB A, EUREK K. A review of operation research in mine planning [J]. Interface, 2010, 40(3): 222–245.

[16] GANGULI R, DAGDELEN K, GRYGIEL E. Mine scheduling and cut-off grade optimization using mixed integer linear programming. Chapter 9.10: Systems Engineering [M]// SME Mining Engineering Handbook (ISBN: 978-0-87335-264-2). 3rd Edition. 2011: 850–852.

[17] ABDEL S S A, DIMITRAKOPOULOS R. Incorporating geological and market uncertainties and operational flexibility into open pit mine design [J]. J Min Sci, 2011, 47(2): 191–201. DOI: 10.1134/S1062739147020067.

[18] DIMITRAKOPOULOS R. Stochastic optimization for strategic mine planning: A decade of developments [J]. Journal of Mining Science, 2011, 47(2): 138–150.

[19] JOHNSON P V, EVATT G W, DUCK P W, HOWELL S D. The determination of a dynamic cut-off grade for the mining industry [C]// Electrical Engineering and Applied Computing, Lecture Notes in Electrical Engineering 90, Chapter 32, 2011: 391–403.

[20] AZIMI Y, OSANLOO M. Determination of open pit mining cut-off grade strategy using combination of nonlinear programming and genetic algorithm [J]. Archives of Mining Sciences, 2011, 56(2): 189–212.

[21] AZIMI Y, OSANLOO M, ESFAHANIPOUR A. Selection of the open pit mining cut-off grade strategy under price uncertainty using a risk based multi-criteria ranking system [J]. Archives of Mining Sciences, 2012, 57(3): 741–768.

[22] ABDOLLAHISHARIF J, BAKHTAVAR E, ANEMANGELY M. Optimal cut-off grade determination based on variable capacities in open-pit mining [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2012, 112(12): 1065–1069.

[23] ASAD M W A, DIMITRAKOPOULOS R. A heuristic approach to stochastic cut-off grade optimization for open pit mining complexes with multiple processing streams [J]. Resources Policy, 2013, 38: 591–597.

[24] AZIMI Y, OSANLOO M, ESFAHANIPOUR A. An uncertainty based multi-criteria ranking system for open pit mining cut-off grade strategy selection [J]. Resources Policy, 2013, 38: 212–223.

[25] NIETO A, ZHANG K Y. Cut-off grade economic strategy for by-product mineral commodity operation: Rare earth case study [J]. Transactions of the Institution of Mining and Metallurgy: Mining Technology, 2013, 122(3): 166–171.

[26] THOMPSON M, BARR D. Cut-off grade: A real options analysis [J]. Resources Policy, 2014, 42: 83–92.

[27] YASREBI A B, WETHERELT A, FOSTER P. Determination of optimized cut-off grade utilizing non-linear programming Arab J Geosci, 2015, 8(10): 8963–8967. DOI: 10.1007/ s12517-014-1756-5.

[28] RAHIMI E, ORAEE K, SHAFAHI T.Z, GHASEMZADEH H. Considering environmental costs of copper production in cut-off grades optimization [J]. Arab J Geosci, 2014, 8(9): 1–15. DOI: 10.1007/s12517-014-1646-x.

[29] RAHIMI E, ORAEE K, SHAFAHI Z, GHASEMZADEH H. Determining the optimum cut-off grades in sulphide copper deposits [J]. Archives of Mining Sciences, 2015, 60(1): 313–328. DOI: 10.1515/amsc-2015-0021.

[30] RAHIMI E, AKBARI A. Application of KKT in determining the final destination of mined material in multi-processing mines [J]. Resources Policy, 2016, 50: 10–18. DOI: org/10.1016/ j.resourpol.2016.08.003.

[31] AKBARI A, RAHIMI E. The effect of copper slag recovery on hydrometallurgical cut-off grades considering environmental aspects [J]. Journal of Central South University, 2016, 23(4): 798–807. DOI: 10.1007/s11771-016-3126-9.

[32] GOODFELLOW R, DIMITRAKOPOULOS R. Global optimization of open pit mining complexes with uncertainty [J]. Applied Soft Computing, 2016, 40: 292–304.

[33] JOHNSON T B. Optimum open pit mine production scheduling [D]. Berkeley: Operations Research Department, University of California, 1968; 539–562.

[34] JOHNSON T B. Optimum production scheduling [C]// Processing of the 8th International Symposium on Computers and Operations Research. 1969: 539–562.

[35] DAGDELEN K. Optimum multi-period open pit mine production scheduling [D]. Colorado: Colorado School of Mines, Golden, 1985.

[36] DAGDELEN K, JOHNSON T B. Optimum open pit mine production scheduling by Lagrangian parameterization [C]// 19th International Symposium on the Application of Computers and Operations Research in the Mineral Industry (APCOM) Ch, 1986, 13: 127–142.

[37] KAWAHATA K. A new algorithm to solve large scale mine production scheduling problems by using the Lagrangian relaxation method [D]. Colorado School of Mines, 2007.

[38] BOLAND N, DUMITRESCU I, FROYLAND G, GLEIXNER A M. LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity [J]. Computer Operation Research, 2009, 36(4): 1064–1089.

[39] MOOSAVI E, GHOLAMNEJAD J, ATAEE-POUR M, KHORRAM E. Optimal extraction sequence modelling for open pit operation considering dynamic cut-off grade [J]. Mineral Resources Management, 2014, 30(2): 173–186.

[40] MOOSAVI E,GHOLAMNEJAD J. Long-term production scheduling modeling for the open pit mines considering tonnage uncertainty via indicator kriging [J]. Journal of Mining Science, 2015, 51(6): 1226–1234.

[41] AKAIKE A, DAGDELEN K. A strategic production scheduling method for an open pit mine [C]// Proceedings of the 28th Application of Computers and Operation Research in the Mineral Industry. 1999: 729–738.

[42] MOGI G, ADACHI T, AKAIKE A, YAMATOMI J. Optimum production scale and scheduling of open pit mines using revised 4D network relaxation method [C]// Proceedings of the 17th International Symposium on Mine Planning and Equipment Selection. 2001: 337–344.

[43] KUMRAL M, DOWD P A. Short-term mine production scheduling for industrial minerals using multi-objective simulated annealing [C]// 2002-International Symposium on the Application of Computers and Operations Research in the Minerals Industry. Littleton, Colorado, 2002: 731–741.

[44] KUMRAL M, DOWD P A. Simulated annealing approach to mine production scheduling [J]. Journal of the Operational Research Society, 2005, 56: 922–930.

[45] GODOY M C, DIMITRAKOPOULOS R. Managing risk and waste mining in long-term production scheduling [J]. Trans of SME, 2004, 316: 43–50.

[46] CONSUEGRA F R A, DIMITRAKOPOULOS R. Stochastic mine design optimization based on simulated annealing: Pit limits, production schedules, multiple orebody scenarios and sensitivity analysis [J]. Transactions of the Institution of Mining and Metallurgy, Section A: Mining Technology, 2009, 118(2): 79–90.

[47] SHISHVAN M S, SATTARVAND J. Long term production planning of open pit mines by ant colony optimization [J]. European Journal of Operational Research, 2015, 24(3): 825–836.

[48] KHAN A, NIEMANN-DELIUS C. Production scheduling of open pit mines using particle swarm optimization algorithm [J]. Advances in Operations Research, 2014, Article ID 208502. DOI: http://dx.doi.org/10.1155/2014/ 208502.

[49] LAMGHARI A, DIMITRAKOPOULOS R. A diversified Tabu search approach for the open-pit mine production scheduling problem with metal uncertainty [J]. European Journal of Operational Research, 2012, 222(3): 642–652.

[50] RAHIMI E, GHASEMZADEH H. A new algorithm to determine optimum cut-off grades considering technical, economical, environmental and social aspects [J]. Resources Policy, 2015, 46: 51–63.

[51] RAMAZAN S. The new fundamental tree algorithm for production scheduling of open pit mines [J]. European Journal of Operational Research, 2007, 177(2): 1153–1166.

[52] WANG Q, GU X, CHU D. A dynamic optimization method for determining cutoff grades in underground mines [J]. Mineral Resources Management, 2008, 3(2): 133–142.

[53] LERCH S, GROSSMANN L. Optimum design of open-pit mines [J]. CIM Bulletin, 1965, 58: 47–54.

[54] LERCH S, GROSSMANN L. Optimum design of open pit mines [J]. CIM Transaction, 1965, 68: 17–24.

[55] ZHAO Y, KIM Y C. A new ultimate pit limit design algorithm [C]// 23rd APCOM. 1992: 423–434.

[56] YAMATOMI J, MOGI G, AKAIKE A, YAMAGUCHI U. Selective extraction dynamic cone algorithm for three dimensional open pit designs [C]// 25th APCOM. 1995: 267–274.

[57] GERSHON M E. A linear programming approach to mine scheduling optimization [C]// 17th APCOM. 1982: 483–493.

[58] HUTTAGOSOL P, CAMERON R E. A computer design of ultimate pit limit by using transportation algorithm [C]// 23rd APCOM. 1992: 443–460.

[59] TOLWINSKI B, UNDERWOOD R. An algorithm to estimate the optimal evolution of an open pit mine [C]// 23rd APCOM. 1992: 399–409.

[60] WANG Q, SEVIM H. Enhance production planning in open pit mining through intelligent dynamic search [C]// 23rd APCOM. 1992: 461–471.

(Edited by FANG Jing-hua)

中文导读

矿山生产计划优化算法、开采材料目的地及最终坑限

摘要：在采矿工程经济中，矿山生产计划、开采材料目的地和最终开采极限（UPL）之间存在着整体的联系，而实际信息及其在采矿经济中产生的效应会加强这种联系，因此，建立优化算法来减少经济计算的误差是非常重要的。本文提出一种考虑重要设计参数和经济性的逻辑数学算法，该算法在不同的设计成分之间建立了一个优化的重复过程，并使其将矿山经济参数最大化，产生最大的矿石量和最高的安全度。该模型在截止品位、矿井设计和矿山规划之间建立了新的关系，并通过计算目标提供了最大的效益。结果表明：与以往的生产设计和生产方法相比，矿山生产的净现值提高了3%。

关键词：开采材料目的地；最终坑限；净现值；生产计划

Received date: 2017-02-15; Accepted date: 2017-10-12

Corresponding author: Rahimi ESMAEIL, Assistant Professor; Tel: +98–9124590976; E-mail: se_rahimi@azad.ac.ir; ORCID: 0000- 0002-7669-3574