J. Cent. South Univ. Technol. (2008) 15: 1-5 

DOI: 10.1007/s11771-008-0001-3 

Prediction of grain size for large-sized aluminium alloy 7050 forging during hot forming

YI You-ping(易幼平)¹, FU Xin(付 欣)¹, CUI Jin-dong(崔金栋)¹, CHEN Hua(陈 华)²

(1.Key Laboratory of Modern Complex Equipment Design and Extreme Manufacturing, Ministry of Education,

Central South University, Changsha 410083, China;

2. Southwest Aluminum (Group) Co Ltd, Chongqing 401326, China)

Abstract：A numerical approach for process optimization and microstructure evolution of lager-sized forging of aluminium alloy 7050 was proposed, which combined a commercial FEM code Deform 3D with empirical models. To obtain the parameters of empirical constitutive equation and dynamic recrystallization models for aluminium alloy 7050, the isothermal compression tests of 7050 samples were performed on Gleeble-1500 thermo-simulation machine in the temperature range of 250-450 ℃ and strain rate of 0.01-10 s^-1, and the metallograph analysis of the samples were carried out on a Leica DMIRM image analyzer. The simulation results show that the dynamic recrystallization in the central area of the billet occurs more easily than that on the edge. Repetitious upsetting and stretching processes make the billet deform adequately. Among several forging processes e.g. upsetting, stretching, rounding and flatting, the stretching process is the most effective way to increase the effective strain and refine the microstructure of the billet. As the forging steps increase, the effective strain rises significantly and the average grain size reduces sharply. Recrystallized volume fractions in most parts of the final forging piece reach 100% and the average grain size reduces to 10 mm from initial value of 90 mm.

Key words: aluminium alloy 7050; grain size; forging; FEM simulation

1 Introduction        

7050 wrought aluminium alloy is a desirable structure material for aircraft components due to their high strength to mass ratio, excellent corrosion resistance and high toughness. With more applications of large-sized wrought components in aircraft structure, the size of ingots has become remarkably large. This will inevitably result in some metallurgical defects, such as voids, microcracks, loose structure and microstructural segregation in the core of the heavy forging ingots^[1]. To ensure a good quality of the finished product, these defects should be eliminated during the forging processes. The purpose of the initial forging is to increase the internal deformation for the better void closure, as well as better structural homogeneity and material quality in the core of the ingot. During forging process, the material undergoes a serial of microstructure evolution such as dynamic/static recovery, recrystallization and grain growth^[2-4], which will have a great influence on the quality of the final products. Consequently, it is of great interest to develop reasonable forging processes for improving the internal quality of large forgings. In addition, the finite element method has become one of the most important and effective methods to simulate the forging process^[5-6]. Much work in simulating the microstructure evolution during hot deformation has been done within a wide range of metals and alloys^[7-10]. However, few researches on the microstructure prediction and forging process simulation for 7050 aluminium alloy have been reported.

The aim of this work is to investigate the forging process and predict the grain size for aluminium alloy 7050 large-sized forging by FEM simulation.

2 Models of simulation

2.1 Experiment

Isothermal compression tests of aluminium alloy 7050 were performed on Gleeble-1500 thermo- simulation machine at strain rates of 0.01, 1.00 and 10.00 s^-1, and for each strain rate at the temperatures of 250, 300, 350, 400 and 450 ℃, respectively. The sample was a solid cylinder with a length of 12 mm, and a diameter of 10 mm. The samples were homogenized at 470 ℃ for 48 h and water quenched. In order to minimize the frictions between the samples and die during hot deformation, the flat ends of the sample were recessed to a depth of 0.1 mm to entrap the lubricant of graphite mixed with machine oil. Each sample was heated to deformation temperature at a rate of 10 ℃/s and held for 300s under isothermal conditions. Then the compression tests were carried out with a reduction height of 50%. The sample after compression was rapidly quenched with water to retain the dynamically recrystallized microstructure. The load-displacement data were recorded automatically by the computer control system of the thermal simulator.

Fig.1 shows the true stress-strain curves obtained from isothermal compression test at temperatures from 250 to 450 ℃ with a strain rate of 10 s^-1. The curves show an obvious behaviour of strain softening and hardening, which is a typical character of fine-grained microstructure and dynamic recrystallization. Furthermore, the stresses are sensitively dependent on the temperature.

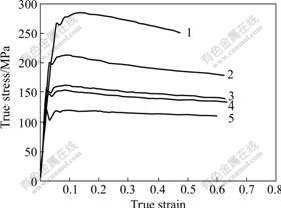
Fig.1 True stress-strain curves at strain rate of 10 s^-1 and different temperatures: 1—250 ℃; 2—300 ℃; 3—350 ℃;  4—400 ℃; 5—450 ℃

For observing and analyzing the microstructure, the samples were sectioned along the longitudinal compression axis, ground and polished. The metallographs in the central region of the section plane were obtained using a Leica DMIRM image analyser (see Fig.2). The parameters used in the constitutive equation and dynamic recrystallization models can be obtained by analysis of these metallographs.

2.2 Constitutive equation

The Arrhenius equation is widely used to describe the relationship among the strain rate, flow stress and temperature at high temperatures^[11-12]. In order to adapt all stress conditions, a hyperbolic sine in Arrhenius type equation containing activation energy Q and temperature T can be expressed as

                   (1)

where A, α and n are the constants independent of temperature, σ^p is the peak stress,is the strain rate, Q is the activation energy for hot deformation, R is the universal gas constant, T is the absolute temperature. By means of regression analysis of experimental results, the values for A, α, n and Q were determined to be 5.83×10¹⁸, 0.012 39, 7.598 and 2.640 6×10⁵ J/mol, respectively. Therefore, the empirical constitutive equation, which can be used to simulate the flow stress in Deform 3D, is written as

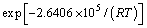                 (2)

Fig.2 Microstructures of aluminium alloy  7050: (a) Before deformation; (b) Deformation at temperature of 300 ℃ and strain rate of 10 s^-1

2.3 Dynamic recrystallization models

It is known that only when dislocation density or strain reaches a critical value can dynamic recrystallization occur during hot deformation. Dislocation density or strain is related with temperature and strain rate. Microstructure evolution is strongly associated with nucleation rate and grain growth kinetics. There are several dynamic recrystallization models for microstructure evolution. For the goal of simulation in this study, the models offered by Deform 3D are adopted, in which the constants can be evaluated by experimental data.

Generally, the onset of dynamic recrystallization occurs at a critical strain ε_c(ε_c=0.8ε_p), and ε_p can be expressed as

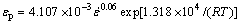       (3)

The Avrami equation used to describe the relationship between the dynamically recrystallized fraction X and the effective strain can be written as

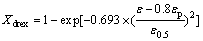             (4)

where  ε_0.5 denotes the strain for 50% recrystallization volume fraction, given as

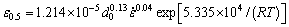          (5)

The recrystallized grain size is expressed as a function of initial grain size, strain, strain rate and temperature, written as

    (6)

The average grain size can be calculated by the equation as

                    (7)

3   Results and discussion

3.1 Forging process and parameters for simulation

Combined with empirical models, FEM code Deform 3D can be used to simulate the free forging process from the initial cylindrical billet with the size of d775 mm×2 200 mm to final product with the size of  2 280 mm×2 220 mm×205 mm. In order to eliminate the metallurgical defects, such as voids, micro-cracks, loose structure and microstructure segregation in the core of this large-sized forging ingot, ten steps forging process including upsetting, stretching, rounding, flattening, squaring, were employed to simulate the whole forging process and the microstructure evolution. To coincide with the practical conditions of industry, the temperature of the billet, the dies and the environment were assumed as 300, 450 and 20 ℃, respectively. The velocity of the upper die was 15 mm/s. Heat transfer was allowed to cross the boundary between the billet and the dies. The friction coefficient between the billet and dies was 0.3. The heat transfer parameters such as convection coefficient, emissivity and thermal conductivity used in the simulation were 20 W/(m²?K), 0.7 and 2 kW/(m²?K), respectively. Substituting the empirical models and the parameters for simulation into Deform 3D input data, forging process and grain size can be simulated. 

3.2 Recrystallized volume fraction and grain size

3.2.1 Volume fraction and grain size of cross-section

Recrystallized volume fraction and grain size are the main characteristic parameters, which can be used to describe the behaviour of microstructure evolution. Fig.3 shows the FE simulation results of cross-section of the billet after the first upsetting. It can be seen that the recrystallized volume fraction in the centre is greater than that on the edge of cross-section (see Fig.3(a)). In the areas contacting with the dies, the recrystallized volume fraction is small. This phenomenon indicates that the dynamic recrystallization in the central area, in which the strain, strain rate and temperature exceed the critical value, will occur easily. On the contrary, the dynamic recrystallization in the area contacting with dies, due to lower strain and temperature, will not take place. It can be concluded that recrystallization behaviour is sensitive to temperature and strain. As shown in Fig.3(b), the average grain size in the area contacting with the dies and in the centre are 90 mm (nearly original grain size) and 41.2 mm, respectively. In comparison with Fig.3(a), it can be drawn that the areas, which have higher recrystallized volume fraction, have smaller average grain size. This is due to the dynamic recrystallization, which will lead to significant grain refinement.

The FE simulation results of cross-section of the billet after the first stretching are shown in Fig.4. From the figure, it can be seen that the dynamic recrystallized volume fractions in most areas are greater than those in the corresponding areas in Fig.3(a), and the maximum volume fraction in the central area in Fig.4(a) reaches 1.0, which means that a complete dynamic recrystallization occurs. Furthermore, the dynamic recrystallization appears in the areas contacting with dies to some extent and the recrystallized volume fraction of these areas reaches 0.3. The reason is that the deformation in the first stretching process is greater than that in the first upsetting process. It can be concluded that the stretching

Fig.3 FE simulation results of billet after the first upsetting:     (a) Recrystallized volume fraction; (b) Average grain size

Fig.4 FE simulation results of billet after the first stretching:     (a) Recrystallized volume fraction; (b) Average grain size

process is effective to increase the effective strain of the billet. Compared with Fig.3(b), the average grain size decreases significantly in Fig.4(b) after the first stretching process, and the maximum and the minimum values are 24.2 and 11.8 mm, respectively. This means the grain size becomes uniform and refined after stretching process.

Fig.5 shows the FE simulation results of cross-section of the billet of the final forging piece. It can be seen from Fig.5 that the dynamic recrystallized volume fractions in most areas of the final forging reach 1 after a series of processing steps including upsetting (three times), stretching (twice), rounding, flattening. The average gain size of the final forging decreases to about 10 mm from original grain size 90 mm. It is proved that all the forging steps, especially stretching and upsetting, are effective to refine the microstructure of the billet and make the grain size uniform.

3.2.2 Grain size of points

Fig.6 shows the relationship between effective strain and the average grain sizes of given two points, that is, P₁, which is in the centre of the billet, and P₂, which is in the top of the billet during the whole deformation course. It can be seen that the effective strain of the two points rises significantly till 12.2 with the increase of the forging steps (Fig.6(a)), whereas the average grain sizes of the two points reduce to 10 mm from original 90 mm sharply as the forging steps increase (Fig.6 (b)). In the beginning, due to low temperature and small effective strain that will lead to inadequate recrystallization, the average grain size of point P₂ decreases slowly. However, it decreases quickly with continuation of forging processes, because of larger effective strain that will lead to a complete dynamic recrystallization. The average grain sizes of points P₁ and P₂ are equivalent at last.

Fig.5 FE simulation results of final forging: (a) Recrystallized volume fraction; (b) Average grain size

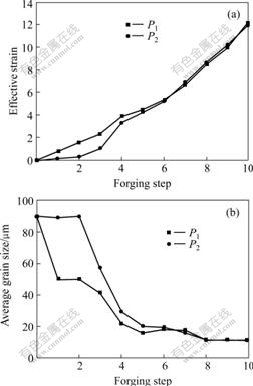
Fig.6 Relationship between effective strain and average grain size in different parts of billet: (a) Effective strain vs steps;   (b) Average grain size vs steps

4 Conclusions

1) Constitutive equation and recrystallization empirical models for aluminium alloy 7050 are obtained by isothermal compression tests and metallograph analysis, which can be used to simulate the forging process.

2) The simulation results indicate that repetitious upsetting and stretching processes can make the billet deform adequately. As the forging steps increase, the effective strain rises significantly, whereas the average grain size reduces sharply.

3) Temperature and effective strain are two impor- tant factors affecting the grain size and recrystallization behaviour when effective strain exceeds the critical value for the given temperature.

4) The recrystallized volume fractions in most of the final forging piece reach 100% and the average grain size reduces to 10 mm from initial value of 90 mm, which meet the industrial demand of refined grain size.

References

[1] POELT P, SOMMITSCH C, MITSCHE S. Dynamic recrystallization of Ni-base alloys—Experimental results and comparisons with simulations[J]. Materials Science and Engineering A, 2006, 420(1/2): 306-314.

[2] SENUMA T, SUEHIRO M, YADA H. Mathematical models for predicting microstructure evolution and mechanical properties of strips[J]. ISIJ International, 1992, 32(3): 423-432.

[3] ZHANG Hui, PENG Da-shu, YANG Li-bing, MENG Li-ping. Recrystallization model for hot-rolling of 5182 aluminium alloy[J]. Trans Nonferrous Met Soc China, 2001, 11(3): 382-386.

[4] FENG Chun, LIU Zhi-yi, NING Ai-ling, ZENG Su-min. Effect of low temperature aging on microstructure and mechanical properties of super-high strength aluminum alloy[J]. Journal of Central South University of Technology, 2006, 13(5): 461-467.

[5] DING R, GUO Z X. Microstructural modeling of dynamic recrystallization using an extended cellular automation approach[J]. Computational Materials Science, 2002, 23(1/4): 209-218.

[6] HARTLEY P, PILLINGER I. Numerical simulation of the forging process[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(48/49): 6676-6690.

[7] SATIO Y. Modelling of microstructure evolution in thermo- mechanical processing of structural steels[J]. Materials Science and Engineering A, 1997, 223(1/2): 134-145.

[8] JANG Y, KO D, KIM B. Application of the finite element method to predict microstructure evolution in the hot forging of steel[J]. Journal of Materials Processing Technology, 2000, 101(1/3): 85-94.

[9] LUCE R, WOLSKE M, ROTERS F, GOTTSTEIN G. Application of a dislocation model for FE-process simulation[J]. Computational Materials Science, 2001, 21(1): 1-8.

[10] ZHANG Jun-hong, HUANG Bai-yun, HE Yue-hui, ZHOU Ke-chao, MENG Li-ping. Physical simulation of hot deformation of TiAl based alloy[J]. Journal of Central South University of Technology, 2002, 9(2): 73-76.

[11] LIN Qi-quan, PENG Da-shu, ZHANG Hui, LIN Gao-yong. Dynamic and static softening behaviours of 2519 aluminium alloy during multi-stage hot compression deformation[J]. Journal of Central South University: Science and Technology, 2005, 36(2): 183-187. (in Chinese)

[12] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling[J]. Materials Science, 1979, 13(3): 187-194.

(Edited by CHEN Wei-ping)

Foundation item: Project(2005CB724105) supported by the National Basic Research Program of China; Project (IRT0549) supported by the Program for Changjiang Scholars and Innovative Research Team in University

Received date: 2007-04-28; Accepted date: 2007-06-12

Corresponding author: YI You-ping, Professor, PhD; Tel:+86-731-8830294; E-mail: yyp@mail.csu.edu.cn