碎石桩复合地基复合模量极限值分析

赵明华，孙建兵，张永杰，张  玲

(湖南大学 岩土工程研究所，湖南 长沙，410082)

摘  要：针对复合地基的复合模量是计算复合地基沉降的关键参数，但求解出完全符合实际的精确解较困难的情况，在分析碎石桩复合地基复合模量现有计算方法及计算中存在的问题基础上，将复合地基看成由桩和土组成的复合材料，从整体上考虑，避免了桩与土之间复杂的相互作用机理分析，并采用弹性理论中最小势能原理和最小余能原理计算复合模量，推求出复合模量上、下限值计算公式。此外，对影响复合模量上、下限值的几个主要参数如桩土压缩模量、土体泊松比和置换率等进行分析。研究结果表明：碎石桩复合地基复合模量极限值随着土体模量和置换率的增大而增大，并且上限值是下限值的1.1~1.4倍，工程实例验证了所求极限值范围的合理性。

关键词： 碎石桩复合地基；复合模量；能量原理；扩大系数

中图分类号：TU 443          文献标志码：A         文章编号：1672-7207(2009)06-1718-06

Limit value of composite modulus of gravel pile composite foundation

ZHAO Ming-hua, SUN Jian-bing, ZHANG Yong-jie, ZHANG Ling

(Geotechnical Engineering Institute, Hunan University, Changsha 410082, China)

Abstract: Based on the fact that the composite modulus of composite foundation is a key parameter in settlement calculations, and that it is hard to obtain precise solutions that are completely conformed to reality, the composite modulus of gravel pile composite foundation and its disadvantages were calculated based on the discussion of the existing method, the calculation formula of the limit value of the composite modulus was obtained, the minimum potential energy principle and the principle of minimum complementary energy were applied, and the gravel pile composite foundation was treated as a composite material composed of pile and soil in this process to avoid the analysis of complex interaction between piles and soil. Moreover, several factors which affect the limit value of the composite modulus such as compression modulus of pile and soil, Poisons’s ratio of soil, replacement ratio were analyzed. The results show that the limit value increases with the increase of soil modulus and replacement ratio, and the upper value is 1.1 to 1.4 times of the lower value. The reasonableness of the limit value calculated is verified by practical engineering projects.

Key words: gravel pile composite foundation; composite modulus; energy principle; expanded coefficient

目前，随着我国高速公路交通网建设的发展，高速公路必然要经过大量的软土地基区域，此时，如何处理软土路基成为公路建设的关键问题之一。以碎石桩作为竖向增强体的复合地基加固技术由于具有沉降小、适应快速加荷以及缩短工期等特点而被广泛采  用^[1]。其相应的工程设计必须满足承载力、沉降与稳定性等要求，其中，有效控制沉降量尤为重要，因此，复合地基沉降计算方法的合理性与可靠性成为工程设计的关键。现有复合地基沉降计算方法中，通常把沉降量分为加固区和下卧层2部分分别计算其压缩量，两者之和即为复合地基总沉降量。对于加固区，常用的压缩量计算方法为复合模量法^[2-3]，其把复合地基加固区中的增强体和基体2部分视为1个复合土体，用复合压缩模量来评价复合土体的压缩性，并采用分层总和法计算。此时，复合模量取值的合理性对沉降计算结果的准确性有决定性的影响，合理取值方法成为复合地基研究的重点与热点之一。为此，《公路路基设计规范》(JTGD 30—2004)^[4]提出按面积加权比进行计算。阎明礼^[3]在总结大量工程实践基础上提出了经验法；张土乔^[5]采用弹性理论建立了相应的计算方法；Schweiger等^[6]推导出有限元计算方法；何思明^[7]基于剪切位移法求出复合模量的计算公式。上述工作对复合模量的研究具有一定的促进作用，但它们有的缺乏理论依据(如经验法)，有的计算过于复杂，其结果未能全面反映桩土的相互作用。为此，本文作者将利用最小势能和最小余能原理，将碎石桩与周围土体作为一个整体考虑，避免桩土之间复杂的应力和相互作用机理分析，进而求得复合模量的上下限值。并对所求上下限值的影响因素进行分析，以便为工程实际中复合模量的合理取值和复合地基沉降范围计算提供参考依据。

1  复合模量常用计算方法分析

现有复合地基的复合模量计算方法主要有公路路基设计规范法、弹性力学分析法、经验法，其具体计算方法如下。

1.1  公路路基设计规范法

《公路路基设计规范》(JTGD 30—2004)^[4]采用面积加权法，公式如下：

该方法形式简单，便于掌握，但其忽略了桩与桩间土的侧向挤压作用。

1.2  弹性理论分析法

张土乔^[5]在假设桩和桩间土变形协调且竖向压缩为常数的前提下，推导出基于弹性理论的复合模量计算公式：

采用式(2)进行推导时，假定应力场与复合地基真实应力场之间存在差别。

1.3  经验方法

阎明礼等^[8]在盛崇文研究的基础上考虑提高桩间土承载力对复合模量的影响，改进了复合模量经验计算公式，为：

该方法与以往经验公式相比更具合理性，但是，其桩间土承载力提高系数是依据工程经验得到的，具有一定的不确定性。

通过上述分析可知，现有复合地基复合模量计算方法均存在一些不足，主要是因为复合地基表现出明显的非均质性，作为一个组合整体，在荷载作用下的应力和应变之间的关系十分复杂，难以采用简单的解析关系表示。因此，对复合模量进行精确且符合实际的力学求解目前仍十分困难，为此，本文作者提出采用能量极值原理求解出其上、下限值，将复合地基作为一个整体进行分析，避免桩与桩间土之间应力与应变关系的分析。

2  基本原理及公式推导

2.1  能量极值原理

能量极值原理用于计算复合材料有效弹性模量上、下限，由Paul率先引用^[9-10]。能量极值原理包括最小势能原理和最小余能原理2个方面。

最小势能原理认为，在边界上满足位移边界条件的容许应变场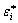所对应的应变能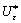，总是大于或等于真实应变场所对应的应变能，即

由于复合地基可以看成是由桩和桩间土组成的复合材料，因此，可以基于能量极值原理来求解其复合模量极限值。

2.2  复合模量上、下限推导

由于应力分布十分复杂^[11]，为便于求解，进行如下假定：

a. 复合地基是宏观均质、各向同性、线弹性的。

b. 基体和增强体在界面处应变连续，不发生相对滑移。

2.2.1  复合模量上限推导

为了分析方便，取由单个桩和所加固范围的土形成的同心圆柱体作为典型的单元体进行计算，结果如图1所示。

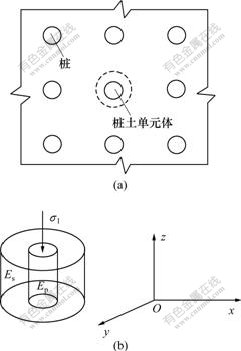
(a) 平面图；(b) 立体图

图1  桩土单元体示意图

Fig.1  Element of pile soil

应用最小势能原理推导上限时，在所取的等效单元体竖向边界上相对位移为0，故复合桩土单元体的容许应变场为：

把式(6)代入式(7)和(8)，可得到桩体和桩间土体容许应力为：

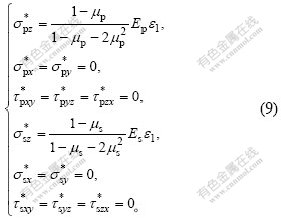
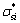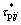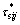式中：为竖向应变；和分别为桩和土容许正应力；和分别为桩和土容许剪应力。

对于线弹性体，其应变能为：

根据(13)式，可求出复合模量的上限值。

2.2.2  复合模量下限推导

应用最小余能原理确定复合模量下限。在所取的复合桩土单元体中，其容许应力场为：

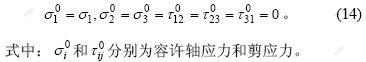
复合桩土单元体在该容许应力场下的余能为：

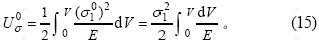
式(15)是在复合桩土单元体整个体积内的积分，可分解为在桩体和土体中分别积分，可得：

由此可确定复合模量的下限值。

3  复合模量极限限分析

3.1  复合模量上限值分析

大量工程实践表明，碎石桩复合地基沉降的计算值一般都远大于实测值^[12]，这说明采用规范法计算复合模量值与实际值相比是偏小的。为此，工程中，常对规范法求得的复合模量进行修正来计算地基沉降，修正值相当于在规范值基础上乘1个系数，但这个系数的范围大多是依据经验取得，缺乏相应的理论依据。

下面分析这个系数的取值问题。首先定义扩大  系数：

。               (19)

式中：为本文计算的上限值；E_c为规范法计算值。下面对影响β的各因素进行分析，计算中，取E_s=   5 MPa，E_p=20 MPa，μ_p=0.25，m=0.25。

3.1.1  置换率

改变置换率，让其在0.1~0.35范围内变化，所得碎石桩扩大系数如图2所示。由图2可知，碎石桩扩大系数随着置换率的增大而减小。因此，在工程中，置换率应控制在一定范围内，以便取得实用、经济的效果。

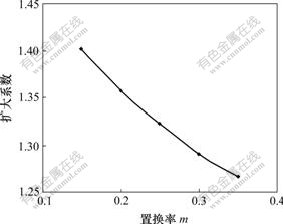
图2  碎石桩扩大系数与置换率的关系

Fig.2  Relationship between expanded coefficient and rate of displacement for gravel pile

3.1.2  泊松比

考虑土体泊松比μ对β的影响时，若取μ=0.2~0.4，可得扩大系数在1.1~1.4之间(图3)。

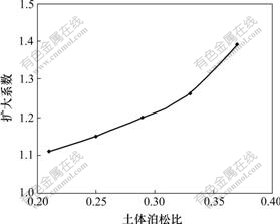
图3  碎石桩扩大系数与土体泊松比的关系

Fig.3  Relationship between expanded coefficient and soil Poisson’s ratio for gravel pile

由图3可见，模量扩大系数随土体泊松比的增大而增大。其原因是土体泊松比越大，桩的侧向鼓胀越大，单元体内部中产生的能量也就越大。

3.2  复合模量下限值分析

对于下限值分析，主要是将由本文方法所得下限值与由规范法所得值进行比较(其中，计算参数取值与上限值分析相同)，分析下限值随各个参数的变化规律。

3.2.1  置换率

图4所示为置换率在常用范围内变化时，碎石桩复合模量上、下限值及规范值的变化情况。

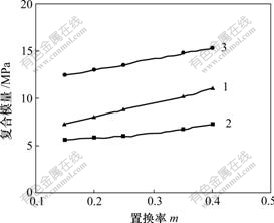
1—规范值；2—下限值；3—上限值

图4  碎石桩复合模量极限值与规范值随置换率变化曲线

Fig.4  Relationships among limit value, code value and rate of displacement for gravel pile

由图4可见，随着置换率增加，下限值有一定增加，但同时下限值与规范值相差越大。

3.2.2  土体模量

考虑土体模量变化对复合模量极限值与规范值之间关系的影响，其计算结果如图5所示。

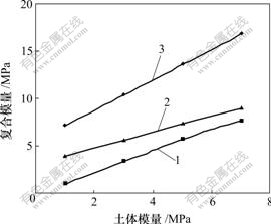
1—下限值；2—规范值；3—上限值

图5  碎石桩复合模量极限值与规范值随土体模量变化曲线

Fig.5  Relationships among limit value, code value and soil body module for composite modulus of gravel pile

从图4和图5可知，由规范法计算的复合模量介于用式(13)和式(18)计算的复合模量上、下限值之间。而由文献[12]可知，由于规范法没有考虑桩土之间的相互作用，使由复合模量规范法所得计算结果与实际值相比是偏小的，因此，考虑到工程经验和实际意义，应取由规范法所得计算值作为复合模量的下限值。

4  算例与分析

4.1  工程实例1

拟建的广东省顺德市挂桥中学其建筑物大多为4层及4层以下的房屋^[13]，而场区存在大面积软土，厚度为30 m。采用13 m长碎石桩处理后，形成复合地基，且场区分3个区，具体地质质料和碎石桩的布置见文献[13]。经过现场加荷，实测场地中三区的沉降量为397.0~477.8 mm。

该算例中各计算参数为：荷载p=96 kPa；桩体泊松比μ_p=0.25；土体泊松比μ_s=0.43，桩体模量E_p=15 MPa；土体模量E_s=3 MPa；桩长H=13 m；置换率m=0.27。根据上述参数可以确定复合模量的上、下限值，进而可以求出复合地基沉降的变化范围。其中，下卧层采用分层总和法计算，沉降计算结果见表1。

4.2  工程实例2

花桥北区B组住宅楼上部为8层砖混住宅楼^[14]，地基采用振冲碎石桩复合地基，原场地为农田，表面呈松散状，下面有淤泥土和亚黏土，故采用碎石桩加固，加固长度为6.5 m，具体方案布置见文献[14]。最后，对沉降分12点进行观测，沉降最大的是5号点，为138.0 mm；最小的是2号点，为81.2 mm。

该算例的计算参数为：荷载p=162 kPa；桩体泊松比μ_p=0.25；土体泊松比μ_s=0.42，桩体模量E_p=20 MPa；土体模量E_s=5 MPa；桩长H=6.5 m；置换率m=0.12。沉降计算结果见表1。

表1  沉降计算值和实测值比较结果

Table 1  Comparison of settlement between calculated values and measured values

通过上面2个工程实例，根据本文推求的复合模量上、下限值，可以看出，复合地基实测的沉降范围均与本文计算的范围基本上相吻合，具有较高的精度。

5  结  论

a. 复合模量上限值是规范值的1.1~1.4倍，可以取规范值作为下限值。

b. 土体模量、土体泊松比及置换率对扩大系数取值均有影响，其中桩间土泊松比的影响显著。在实际工程中，可以根据上述影响参数选取最佳的扩大系数，以确定碎石桩复合地基的复合模量。

c. 工程实例分析结果表明，采用本文方法所得分析结果与实测结果较吻合，进一步验证了采用本文方法所求上、下限值是合理的，也可为工程实际中碎石桩复合地基沉降值预估提供参考。

参考文献：

[1] 赵明华, 张 玲, 刘敦平. 散体材料桩复合地基桩土应力比分析[J]. 中南大学学报: 自然科学版, 2007, 38(3): 555-560.
ZHAO Ming-hua, ZHANG Ling, LIU Dun-ping. Bearing capacity calculating method of discrete material pile composite foundation[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 555-560.

[2] 龚晓南. 复合地基设计和施工指南[M] . 北京: 人民交通出版社, 2003 .
GONG Xiao-nan. Design of composite foundation and construction guide[M]. Beijing: People Traffic Press, 2003.

[3] 阎明礼. 地基处理技术[M]. 北京: 中国环境科学出社, 1996.
YAN Ming-li. Ground treatment techniques[M]. Beijing: China Environmental Science Press, 1996.

[4] JTGD 30—2004, 公路路基设计规范[S].
JTGD 30—2004, Specifications for design of highway sub grades[S].

[5] 张土乔. 水泥土应力应变关系及搅拌桩破坏特性研究[D]. 杭州: 浙江大学土木工程学院, 1992.
ZHANG Tu-qiao. The relationship between stress and strain for soil-cement and damage to properties of mixing pile[D]. Hangzhou: School of Civil Engineering, Zhejiang University, 1992.

[6] Schweiger H F, Pande G N. Numerical analysis of stone column reinforced foundation[J]. Computers and Geotechmics, 1998, 13(2): 347-372.

[7] 何思明. 复合地基压缩模量计算新方法[J]. 四川建筑科学研究, 1997, 16(3): 38-40.
HE Si-ming. The new calculation method of composite modulus for composite foundation[J]. Building Science Research of Sichuan, 1997, 16(3): 38-40.

[8] 阎明礼, 曲秀莉, 刘 伟, 等. 复合地基的复合模量分析[J]. 建筑科学, 2004, 20(4): 27-32.
YAN Ming-li, QU Xiu-li, LIU Wei, et al. Composite modulus analysis of composite foundation[J]. Building Science, 2004, 20(4): 27-32.

[9] 张少实, 庄 茁. 复合材料与粘弹性力学[M]. 北京: 机械工业出版社, 2005.
ZHANG Shao-shi, ZHUANG Zuo. Composite materials and mechanical viscoelastic[M]. Beijing: Machinery Industry Press, 2005.

[10] 范赋群, 王振明, 嵇 醒, 等. 关于复合材料力学几个基本问题的研究[J]. 华南理工大学学报: 自然科学版, 1995, 23(4): 1-5.
FAN Fu-qun, WANG Zhen-ming, JI Xing, et al. Study on several basic problems on mechanics of composites[J]. Journal of South China University of Technology: Natural Science, 1995, 23(4): 1-5.

[11] 张 定. 散体材料桩复合地基的沉降分析与计算[J]. 铁道学报, 1998, 20(6): 98-104.
ZHANG Ding. Settlement analysis & computation for composite foundation of friable material pile[J]. Journal of the China Railway Society, 1998, 20(6): 98-104.

[12] 张 定. 碎石桩复合地基的作用机理分析及沉降计算[J]. 岩土力学, 1999, 20(2): 81-86.
ZHANG Ding. Functional mechanism analysis and settlement computation on composite foundation of gravel pile[J]. Rock and Soil Mechanics, 1999, 20(2): 81-86.

[13] 曹 星, 刘小峰, 定培中. 碎石桩处理深厚层软土地基效果分析[J]. 长江科学院院报, 2000, 17(3): 47-50.
CAO Xing, LIU Xiao-feng, DING Pei-zhong. Effect analysis of treating deep thick soft foundation with crushed-rock piles[J]. Journal of Yangtze River Scientific Research Institute, 2000, 17(3): 47-50.

[14] 杨才晶. 碎石桩复合地基的成功实例[J]. 土工基础, 1994, 8(1): 32-37.
YANG Cai-jing. A successful example of gravel plied pound foundation[J]. Soil Engineering and Foundation, 1994, 8(1): 32-37.

收稿日期：2008-12-06；修回日期：2009-03-15

基金项目：国家高技术研究发展计划(“863”计划)项目(2006AA11Z104)；湖南省研究生创新基金资助项目(2008年)

通信作者：赵明华(1956-)，男，湖南洞口人，教授，博士生导师，从事桩基础及区域性软土地基处理研究；电话：0731-88821590；E-mail: mhzhaohd@21cn.com