J. Cent. South Univ. (2012) 19: 163-167
DOI: 10.1007/s11771-012-0986-5
Pendulation reduction on ship-mounted container crane via T-S fuzzy model
JANG Jae Hoon, KWON Sung-Ha, JEUNG Eun Tae
Department of Control and Instrumentation, Changwon National University, Changwon 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Ship-mounted container cranes are challenging industrial applications of nonlinear pendulum-like systems with oscillating disturbance which can cause them unstable. Since wave-induced ship motion causes the hoisted container to swing during the transfer operation, the swing motion may be dangerously large and the operation must be stopped. In order to reduce payload pendulation of ship-mounted crane, nonlinear dynamics of ship-mounted crane is derived and a control method using T-S fuzzy model is proposed. Simulation results are given to illustrate the validity of the proposed design method and pendulation of ship-mounted crane is reduced significantly.
Key words: ship-mounted crane; disturbance; pendulation control; T-S fuzzy model
1 Introduction
The pendulation problems of crane-payloads have received considerable attention over the last decades. Various types of controllers for cranes have been designed, such as optimal control [1], sliding mode control [2], adaptive control [3], fuzzy control [4-5], feedback linearization control [6], gain scheduling control [7], input shaping control [8-9], and disturbance observer based control [10]. These controllers were designed without considering excitations of the base of the crane, as in ship-mounted cranes.
Ship-mounted container cranes are used for transferring containers between large and small container ships when deep-water ports are not available for the container ships. Since wave-induced ship motion causes the hoisted container to swing during the transfer operation, the swing motion may be dangerously large and the operation must be stopped. Since much time and money is wasted to wait for acceptable sea conditions to operate, it is of great value to develop a ship-mounted container crane for the transfer operation in sea state as defined by Pierson-Moskowitz Sea Spectrum with 1-1.6 m significant wave height [11-14].
Ship-mounted container cranes are challenging industrial applications of nonlinear pendulum-like systems with oscillating disturbance which can cause them unstable. In order to reduce payload pendulation of ship-mounted crane, the delayed-position feedback control using PD tracking controllers [12-14] and position/velocity-based inverse kinematic pendulation control [15] were proposed.
In this work, a control method using T-S fuzzy model to reduce payload pendulation of ship-mounted cranes is proposed. T-S fuzzy model is well known for good representations of nonlinear dynamic systems [16]. Since T-S fuzzy model has linear dynamics in consequent parts and its output is interpolated by membership functions, its control problem is similar to linear control.
2 Dynamics of ship-mounted container crane
Consider the model of the ship-mounted container crane as shown Fig. 1. For simplicity, its dynamics is considered only on YZ-plane and the following items are assumed:
1) The trolley and payload are assumed to be modeled as each point mass.
2) The cable connected to the payload is a massless rigid rod and has a fixed length.
3) All frictional elements are negligible.
4) The ship-mounted container crane is disturbed by the ship roll, not heave and pitch. The position, velocity, and acceleration of the roll motion are measurable.
Figure 1 shows sway motion of the payload caused by the trolley movement and the ship roll. The position vector of the trolley with respected to the fixed-axis coordinate system is
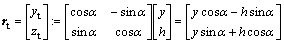 (1)
(1)
And the position vector of the spreader with respected to the fixed-axis coordinate system is
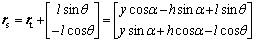 (2)
(2)
where h is the fixed height of the crane, y is the displacement of the trolley on the boom, l is the fixed cable length, α is the angle of the ship roll, and θ is the angle between the gravitational direction and the line of the spreader on the YZ-plane.
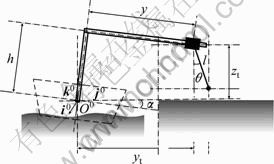
Fig. 1 Ship-mounted container crane on YZ-plane
The kinetic and potential energies of the system are, respectively, expressed as
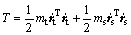 (3)
(3)
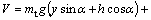
 (4)
(4)
where
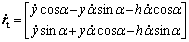 (5)
(5)
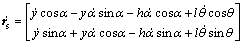 (6)
(6)
mt is the mass of the trolley, ms is the mass of the payload, θ is the sway angle of the load, and g is the gravitational acceleration.
The Lagrangian function is given as
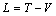 (7)
(7)
Taking y and θ as the generalized coordinates, the equations of motion can be derived as
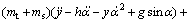
 (8)
(8)
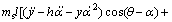
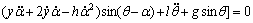 (9)
(9)
The dynamic equations (8) and (9) can be rewritten as
 (10)
(10)
where
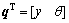
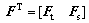
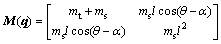
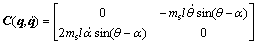
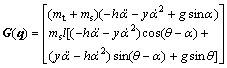 (11)
(11)
or
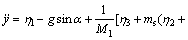
 (12)
(12)
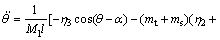
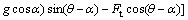 (13)
(13)
where
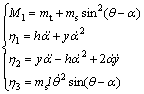 (14)
(14)
It is remarked that the inertia matrix M(q) is always symmetric but  satisfies the skew- symmetric relationship when
satisfies the skew- symmetric relationship when 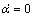 or
or 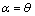 .
.
The ship-mounted container crane is excited by roll motion of the ship. Figure 2 shows the angle of the payload for a sinusoidal roll motion with amplitude of 3° at a frequency of 0.159 Hz when the position of the trolley is fixed at 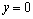 (that is,
(that is, 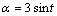 and
and  ). This frequency will excite the primary resonance of the load with the cable length of 9.8 m.
). This frequency will excite the primary resonance of the load with the cable length of 9.8 m.
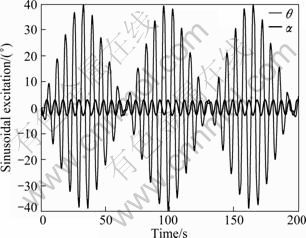
Fig. 2 Computer simulation results for sinusoidal excitation in ship roll
Using the variables yt and zt from Eq. (1), the equations (8) and (9) can be rewritten as
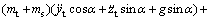
 (15)
(15)
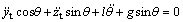 (16)
(16)
where yt and zt imply, respectively, the Y-directional and Z-directional displacements of trolley in the fixed coordinate.
Let
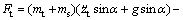
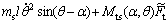 (17)
(17)
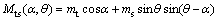 (18)
(18)
Then, the dynamics is
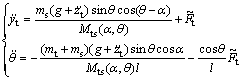 (19)
(19)
The dynamics Eq. (19) is available when Mts(α, θ) is invertible. Figure 3 shows a contour plot of [Mts(α, θ)]/mt as a function of α and θ when ms=2mt. For example, when θ=30° and α=60° (or θ=-30°, α=-60°), Mts(α, θ) is not invertible. In the case of ms=2mt, Mts(α, θ) is invertible if |α|<60°.
The suprema of the following set are summarized in Table 1.
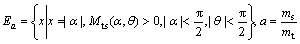 (20)
(20)
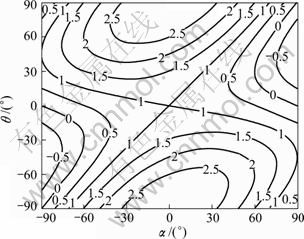
Fig. 3 Contour plot of [Mts(α, θ)]/mt when ms/mt=2
3 T-S fuzzy model and control
The cable sway of the crane system is assumed by a small angle approximation (that is, θ≈0), Mts(α, θ) of Eq. (19) can be approximated to  (21)
(21)
And an approximated model of the dynamics Eq. (19) can be reduced to
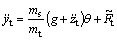
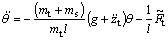 (22)
(22)
Table 1 Suprema of set Ea of Eq.(20)

The system Eq. (22) is same to a linearized pendulum system under an assumption ( ), but the assumption is not acceptable because the container crane has a roll motion due to wave-excited motion. In order to design a controller for the nonlinear system Eq. (22), T-S fuzzy model is applied. The T-S fuzzy model of Eq. (21) can be constructed as follows:
), but the assumption is not acceptable because the container crane has a roll motion due to wave-excited motion. In order to design a controller for the nonlinear system Eq. (22), T-S fuzzy model is applied. The T-S fuzzy model of Eq. (21) can be constructed as follows:
Rule 1
IF 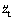 is about a,
is about a,
THEN  .
.
Rule 2
IF 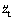 is about -a,
is about -a,
THEN 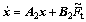 .
.
Here, α is a positive constant,
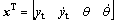 ,
,
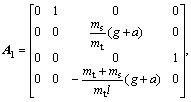
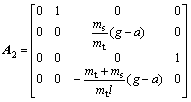 ,
,
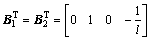 .
.
The above T-S fuzzy model can be represented as
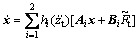 (23)
(23)
where
 (24)
(24)
The following PDC (parallel distributed compensation) fuzzy controller is considered as a controller for the T-S fuzzy model Eq. (23):
Control Rule 1
IF 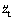 is about a,
is about a,
THEN 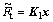 .
.
Control Rule 2
IF 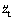 is about -a,
is about -a,
THEN  .
.
It is well-known that a sufficient condition of existing a PDC controller for T-S fuzzy system is represented as the following LMI (linear matrix inequality) feasibility problem.
Sufficient condition [17]: The equilibrium of the T-S fuzzy system Eq. (22) is globally asymptotically stable if there exist a positive definite matrix Q and matrices Ni (i=1, 2) such that
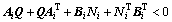 (25)
(25)
Furthermore, PDC fuzzy control gains are 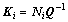 .
.
With the parameters of the crane system as follows:
mt=10 000 kg, ms=10 000 kg, g=9.8 m/s2, l=9.8 m
PDC fuzzy control gains are
 (26)
(26)
when α=5. The simulation results are shown in Fig. 4 when the disturbance of ship roll input is α=3sint. In Fig. 4(a), ytr is the reference input of yt and y is the displacement of the trolley. Figure 4(a) shows that the position of the payload is tracked to the reference position in spite of the ship rolling and Fig. 4(b) shows that payload pendulation of ship-mounted crane is also reduced quite a lot by comparison with Fig. 2.
4 Conclusions
Ship-mounted container cranes are challenging industrial applications of nonlinear pendulum-like systems with oscillating disturbance which can cause them unstable. In order to reduce payload pendulation of ship-mounted crane, a control method using T-S fuzzy model to reduce payload pendulation of ship-mounted cranes is proposed. The computer simulations have been illustrated to verify the proposed design method. Dangerous pendulation due to wave-induced ship motion is reduced significantly.
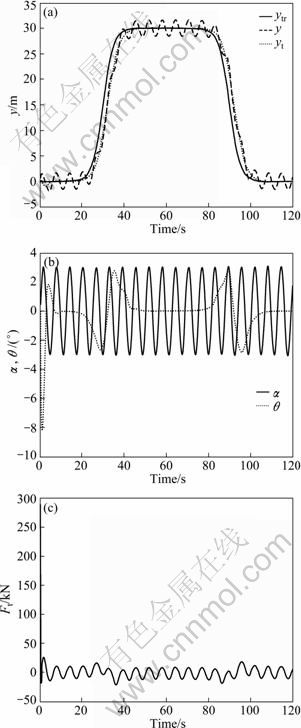
Fig. 4 Simulation results: (a) Reference position of payload ytr, position of trolley y and payload yt; (b) Disturbance of ship roll α=3sint and payload angle θ; (c) Control input Ft
References
[1] AL-GARNI A Z, MOUSATAFA K A F, JAVEED NIZAMI S S A K. Optimal control of overhead cranes [J]. Control Engineering Practice, 1995, 3(9): 1277-1284.
[2] BARTOLINI G, PISANO A, USAI E. Second-order sliding mode control of container cranes [J]. Automatica, 2002, 38(10): 1783-1790.
[3] YANG J H, YANG K S. Adaptive coupling control for overhead crane systems [J]. Mechatronics, 2007, 17(2/3): 143-152.
[4] CHO S K, LEE H H. A fuzzy-logic antiswing controller for three- dimensional overhead cranes [J]. ISA Transactions, 2002, 41(2): 235-243.
[5] CHANG C Y, CHIANG K H. Fuzzy projection control law and its application to the overhead crane [J]. Mechatronics, 2008, 18(10): 607-615.
[6] PARK H, CHWA D, HONG K S. A feedback linearization control of container cranes: Varying rope length [J]. International Journal of Control, Automation, and Systems, 2007, 5(4): 379-387.
[7] OMAR H M, NAYFEH A H. Gantry cranes gain scheduling feedback control with friction compensation [J]. Journal of Sound and Vibration, 2005, 281(1/2): 1-20.
[8] HONG K T, HUH C H, HONG K S. Command shaping control for limiting the transient sway angle of crane systems [J]. International Journal of Control, Automation, and Systems, 2003, 1(1): 43-53.
[9] SORENSEN K L, SINGHOSE W E, DICKERSON S. A controller enabling precise positioning and sway reduction in bridge and gantry cranes [J]. Control Engineering Practice, 2007, 15(7): 825-837.
[10] SAWODNY O, ASCHEMANN H, LAHRES S. An automated gantry crane as a large workspace robot [J]. Control Engineering Practice, 2002, 10(12): 1323-1338.
[11] VAUGHERS T. Joint logistics over the shore operations [J]. Naval Engineers Journal, 1994, 106(3): 256-263.
[12] MASOUD Z N. A control system for the reduction of cargo pendulation of ship-mounted cranes [D]. Virginia: Virginia Polytechnic Institute and State University, 2000.
[13] HENRY R J, MASOUD Z N, NAYFEH A H, MOOK D T. Cargo pendulation reduction of ship-mounted cranes via boom-luff angle actuation [J]. Journal of Vibration and Control, 2001, 7: 1253-1264.
[14] MASOUD Z N, DAQAQ M E, NAYFEH N A. Pendulation reduction on small ship-mounted telescopic cranes [J]. Journal of Vibration and Control, 2004, 10: 1167-1179.
[15] SCHAUB H. Rate-based ship-mounted crane payload pendulation control system [J]. Control Engineering Practice, 2008, 16(1): 132-145.
[16] TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control [J]. IEEE Trans Syst, Man, Cybern, 1985, 15: 116-132.
[17] TANAKA K, IKEDA T, WANG H O. Fuzzy regulators and fuzzy observers: Relaxed stability conditions and LMI-based designs [J]. IEEE Trans Fuzzy Systems, 1998, 6(2): 250-265.
(Edited by YANG Bing)
Foundation item: Work supported by Changwon National University in 2011-2012; work partly supported by the second stage of Brain Korea 21 Projects
Received date: 2011-04-26; Accepted date: 2011-10-10
Corresponding author: JEUNG Eun Tae; Tel: +82-55-213-3667; E-mail: jet26@changwon.ac.kr