J. Cent. South Univ. (2020) 27: 1780-1789

DOI: https://doi.org/10.1007/s11771-020-4407-x

Galerkin-based extended Kalman filter with application to CO₂ removal system

LV Ming-bo(吕明博), LI Yun-hua(李运华), GUO Rui(郭锐)

School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: The carbon dioxide removal system is the most critical system for controlling CO₂ mass concentration in long-term manned spacecraft. In order to ensure the controlling CO₂ mass concentration in the cabin within the allowable range, the state of CO₂ removal system needs to be estimated in real time. In this paper, the mathematical model is firstly established that describes the actual system conditions and then the Galerkin-based extended Kalman filter algorithm is proposed for the estimation of the state of CO₂. This method transforms partial differential equation to ordinary differential equation by using Galerkin approaching method, and then carries out the state estimation by using extended Kalman filter. Simulation experiments were performed with the qualification of the actual manned space mission. The simulation results show that the proposed method can effectively estimate the system state while avoiding the problem of dimensional explosion, and has strong robustness regarding measurement noise. Thus, this method can establish a basis for system fault diagnosis and fault positioning.

Key words: carbon dioxide removal system; Galerkin; infinite nonlinear filter; extend Kalman filter

Cite this article as: LV Ming-bo, LI Yun-hua, GUO Rui. Galerkin-based extended Kalman filter with application to CO₂ removal system [J]. Journal of Central South University, 2020, 27(6): 1780-1789. DOI: https://doi.org/10.1007/ s11771-020-4407-x.

1 Introduction

Environment control and life support system (ECLSS) is one of the indispensable key systems in the space station, which guarantees safety and health of the astronauts [1-4]. The carbon dioxide removal system (CDRS) is one of the key subsystems in ECLSS [5, 6]. During the service period of the space station in orbit, as a key component of the air revitalization system, the carbon dioxide adsorption tower, its state directly determines the air quality in the sealed cabin. When CDRS fails, the cargo spacecraft is unable to timely transport new equipment and materials to repair the system [7], non-renewable carbon dioxide removal equipment will be turned on. With the gradual consumption of LiOH in the non-renewable removal equipment, the carbon dioxide in the cabin fails to be removed. Thus the concentration of carbon dioxide in the cabin will gradually increase. When the volume fraction of carbon dioxide in the air is 0.1%, slight nausea, dizziness and palpitations will occur to people in the cabin. When the volume fraction of carbon dioxide raises to 0.4%-0.5%, and people inside will feel dizzy. When it is more than 0.6%, people are unconscious and gradually stop breathing and then die [8, 9]. Therefore, it is necessary to detect the operation status of the adsorption tower online [10]. This undergoing is more urgent for China, which has successfully launched Tiangong-1 [11] and Tiangong-2 [12], and will establish a long-term space station in orbit in the future [13]. The relevant research should be carried out in the subsequent developing process, so that it can be applied to the actual operation process as soon as possible.

Taking the International Space Station as an example, the kernel device in the carbon dioxide removal system is an adsorption tower, and the molecular sieve in it is used to adsorb carbon dioxide. Due to the special structure of the adsorption tower, the measuring device can only be placed at the adsorption tower vent. In addition, the concentration of carbon dioxide in the cabin can also be detected by the detection device in real time. However, the CO₂ concentration in the capsule is not a suitable index for judging whether the carbon dioxide removal system is operating normally. It is known that the CO₂ concentration in the capsule is a slow varying parameter and the response is lag, especially in the large volume storage conditions of the space station. Thus, the concentration of CO₂ at the vent of the adsorption column can be selected as the direct index parameter for online monitoring. However, this parameter is not measurable and needs to be estimated using existing observable measurements.

Two main steps need to be undergone for the estimation of this dynamic parameter. Firstly, a model is established which describes the dynamic change of the parameter. And secondly, a suitable state observer for the model is designed. For the former, the CO₂ adsorption mode of CDRS is a physical adsorption process. The dynamic model of CDRS can be established for the system, according to the system’s operating mechanism and operating conditions [14-16]. Currently, the generally recognized solution is a dynamic process described by a set of partial differential equation (PDE) [17]. In this model, the carbon dioxide concentration in the air passing through the adsorption tower does not only vary with time, but also relates to the axial coordinates of the adsorption tower. In addition, the amount of carbon dioxide adsorbed will also appear as a state variable of the system in the model. And it is also a function of time and axis coordinates, and cannot be discarded as a model error [18]. Therefore, the adsorption process appears as to be a typical multi-dimensional distributed model. After the mathematical model of the adsorption process is obtained, it is utilized for the design process of the state observer. The model needs to be approximated through Galerkin [19, 20] method to obtain the corresponding ordinary differential equation (ODE) equation, which is described by the PDE equation. And the state observer can be designed. The traditional state observers or filters, such as SMO [21, 22] and EKF [23, 24], are designed for finite-dimensional systems and unable to be directly used in multidimensional distributed models [25, 26]. However, these studies are directed at one- dimensional systems, rather than multi-dimensional systems. In response to the above problems and CDRS’s distinctiveness, Galerkin method is extended to a multi-dimensional system [27, 28], and a G-EKF filter was designed. In this paper, the simultaneous approximation of two-state variable is used in the process of PDE approximating ODE, which not only conforms to the actual physical process, but also ensures the approximate accuracy of the method. Through simulation experiments in this paper, the method is successfully applied to the estimation of adsorption tower’s adsorption amount of CO₂ and the outlet concentration in CDRS of the space station.

The rest of the article is organized as follows. In Section 2, the role and the work flow of the CDRS in the space station are outlined briefly, and in Section 3, the EKF method based on Galerkin for two-dimensional partial differential equation is outlined briefly. In Section 4, the application of Galerkin-based EKF method in estimating the concentration of adsorbate is shown in detail, and in Section 5, the simulation results illustrate the efficacy of the model reduction and estimation schemes. In Section 6, the main conclusions of the article are summarized.

2 Working principle and dynamic model of CDRS

The role of the CDRS in the manned spacecraft is to control the CO₂ concentration in the cabin within the allowable range, and the working procedure of CDRS is shown in Figure 1. The CDRS extracts air from the cabin into the adsorption tower of the system, and CO₂ is adsorbed when the air containing the high concentration of CO₂ passes through the adsorbent bed of the adsorption tower.

The adsorption tower comprises two adsorption beds, and they take turns to work. After adsorption for 3 h, one bed is saturated and then desorbed by heating the bed. The adsorbent bed releases CO₂, which is directly discharged into space. After continuous adsorption and desorption of two adsorption beds, the CO₂ concentration in the cabin gradually decreases, and when the CO₂ concentration in the cabin drops to a normal level, the adsorption bed stops working.

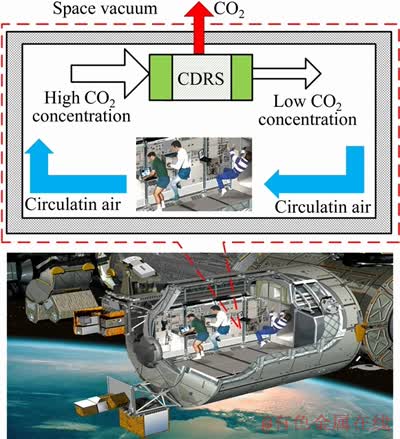
Figure 1 Working procedure of CDRS in manmade spacecraft cabin

Nowadays, the molecular sieve is used as the adsorption equipment of CDRS [29], as shown in Figure 2. In the cabin, the air containing water vapor enters the drying bed I from the inlet of the adsorption tower, and then the dried air is cooled by passing through a cooled pre-cooler. The cooled air enters the adsorption bed II containing the adsorbent material, and the air containing the high concentration of CO₂ passes through the adsorption bed filled with 5A molecular sieve material. Because the diameter of the CO₂ molecule is smaller than the diameter of N₂ and O₂ molecules, CO₂ will be selectively adsorbed by the molecular sieve material filled in the adsorption bed [30, 31]. The adsorbent bed generates heat after adsorbing CO₂, which will heat the gas. The gas stream which has been subjected to the adsorption treatment is sent to the drying bed II to be dried again. At this point, half of the entire adsorption process is completed. The other half cycle is just the opposite.

Through the above-mentioned workflow, it can be seen that the air flow in the cabin is sent to the adsorption tower by the blower, and the CO₂ contained in the airflow is absorbed by the adsorbent material when passing the adsorption bed [32]. There are some quantities need to be neglected during the establishment of the model, including eddy current diffusion, internal diffusion and axial diffusion during the adsorption process. In addition, adsorption equilibrium constants, mass transfer resistance coefficient packing densities, etc. are known. Therefore, the kinetic model of the adsorption process of the adsorbent bed can be established as follows:

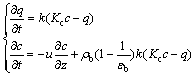            (1)

where q is the amount of adsorbed carbon dioxide;c is the mass concentration of the adsorbate; K_c is the adsorption equilibrium constant; u is the traversing speed; k is the mass transfer coefficient; ρ_b is the solid density; ε_b is the bulk density. Obviously, this is a two-dimensional partial differential equation.

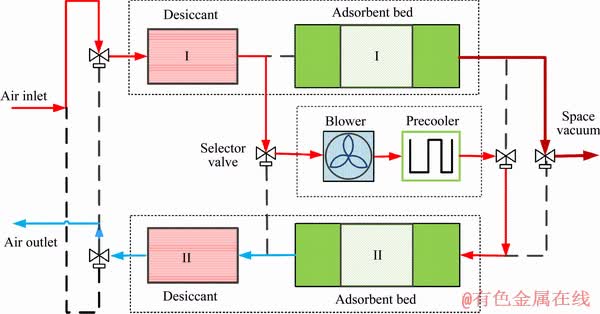
Figure 2 Schematic diagram for 4-BMS adsorption/desorption processes

In general, the mass flow sensor is deployed at the outlet of adsorption tower. Based on the law of the mass conservation, the mass flow rate can be described as follows:

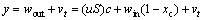           (2)

where v_t is the zero mean Gaussian white noise and x_c is the mass fraction which is described as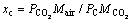with P_CO2 and P_C are the partial pressure of CO₂ and cabin pressure, respectively.

3 Galerkin-based extend Kalman filter

3.1 Galerkin approximation

For Eq. (1), it can be described as the following general form:

                        (3)

where 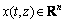is a single dimension state variable; z is the space coordination; and 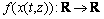is the C ^∞ function.

If we assume x(t, z) belongs to a subspace of a Hilbert space, x(t, z) can be expressed by Fourier form as:

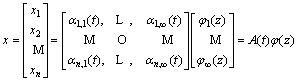 (4)

where φ_i(z) is the basis function on Hilbert space; α_i(t) is the Fourier coefficient. Obviously, if we intercept the finite items in Eq. (4), then the state estimation can be approximated as follows:

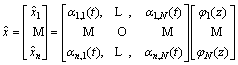
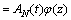                            (5)

where N is a large enough positive integer.

Substituting Eq. (5) into Eq. (3), the system residual R(t, z) can be calculated as follows:

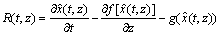
           (6)

The Galerkin method demands the Fourier coefficients satisfy the following conditions:

            (7)

Substituting Eq. (6) into Eq. (7) yields

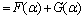                        (8)

Interior point calculation can be assigned to each element because Hilbert interior point is a linear operator. F(α) and G(α) can be calculated by the following expressions:

 (9)

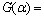
 (10)

3.2 EKF based on Galerkin approximation

For the finite ODE Eq. (8), the Galerkin-based EKF approximation can be designed. Because A(t) is a n×N dimensional matrix, the ODE can be obtained which is used as the filter equation to the EKF algorithm. The dynamic equation of each Fourier coefficient can be described as follows:

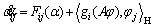                 (11)

where F_ij(a_ij) is the i-th row and j-th column element of F(α).

Based on the above discussions, the Galerkin-based EKF algorithm can be summarized as extend Kalman filter algorithm based on Galerkin method shown in Table 1.

Table 1 Extend Kalman filter algorithm based on Galerkin method

In the Galerkin-based EKF algorithm, the Jacobi matrix J_F can be calculated as follows:

                      (12)

The i-th row and j-th column element of the Jacobi matrix J_H can be calculated as follows:

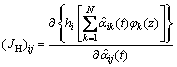             (13)

In addition, 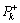and 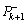are the posteriori error covariance at t_k and the priori error covariance at t_k+1, respectively; K is the Kalman gain; y_k+1 is measurements at t_k+1.

4 Galerkin-based EKF algorithm of absorption process

The models of CO₂ removal system and Galerkin-based EKF have been established in the previous paper. The Galerkin-based EKF can be applied to CO₂ removal process.

According to Eq. (1), the model of CO₂ removal system can be written as follows:

                    (14)

where

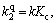
Letdenote the state variable, f(x) and g(x) can be obtained:

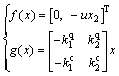                      (15)

where u is the transmitting speed of CO₂.

The Fourier expansion can be written as

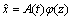                            (16)

where

                 (17)

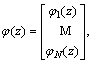
         (18)

Substituting Eqs. (15), (17) and (18) into Eq. (8), F(α) and G(α) can be expressed as follows:

 (19)

In Eq. (19), the specific expression of F(α) can be derived as follows. Considering the partial derivative of φ(z) can be derived as

                (20)

We can calculate F(α) from three cases which are j=1, and 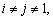respectively.

When j=1,

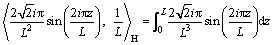
                (21)

When

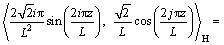
               (22)

When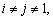

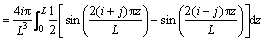
                                (23)

where φ_i(z) is the basis function on Hilbert space.

Thus, F(α)=0.

In summary, the state equation used for the EKF algorithm can be obtained as follows:

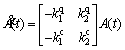                     (24)

Let 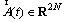is a vector that straightens matrix A(t) by rows. According to Eq. (24), the state transition matrix can be written as:

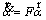                                (25)

where the state transfer matrix F can be written as follows:

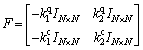                   (26)

The output equation of the adsorption tower model is represented by Eq. (2), and the system output equation can be written as

     (27)

Obviously, the infinite-dimensional equations that characterize the adsorption process are approximated by using the Galerkin method, which is approximated as a linear system. The Galerkin-based EKF degenerates Galerkin-based KF.

5 Simulation results

During the actual space station operation, a complete adsorption cycle of the CDRS is 3 h and the length of adsorption bed is 0.5 m. The diameter of the cavity portion in the adsorption tower is 0.2 m, and the value of u in Eq. (1) is 0.25 m/s. The order of the Fourier expansion is N=6, and R=diag(10^-4). Therefore, these restrictions are also the conditions of the simulation experiment in this paper. The values of experimental data are obtained in the simulation experiment under these experimental conditions.

The estimation performance comparison of true value and simulation experiment result with Galerkin-based EKF are shown in Figures 3 and 4. Figure 3 shows the estimation of c with Galerkin- based EKF and Figure 4 shows the estimation result of q. In the first 1.5 h, the adsorption rate of carbon dioxide in the adsorption tower is fast, and the adsorption capacity has hardly been attenuated. With the passage of time, the adsorption capacity of adsorption tower decreased gradually. After 3 h of adsorption, the adsorption tower gradually saturated. In the whole process of adsorption, using the Galerkin-based EKF can track the true adsorption curve very well.

Monte Carlo method is used to show the variance comparison between true value and simulation experiment value with Galerkin-based EKF in 50 epochs. The comparison results are shown in Figures 5 and 6, the accuracy of the estimation method can be better expressed by using normalization mean square error (NMSE) in the ordinate. Obviously, the accuracy of the Monte Carlo method reached 1×10^-3 level, and the estimation accuracy has not changed greatly. The simulation experiment results obtained by Galerkin- based EKF method can track the true values excellently, and robust to the model error.

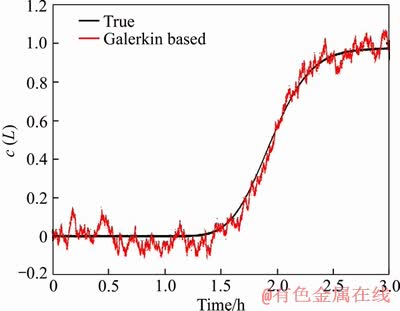
Figure 3 Estimation of c (L) with Galerkin-based EKF

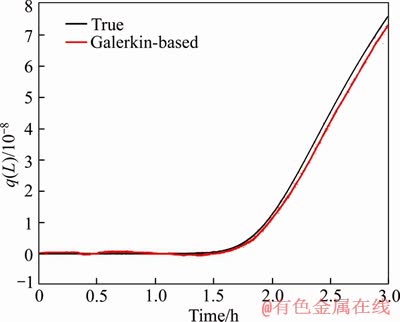
Figure 4 Estimation of q (L) with Galerkin-based EKF

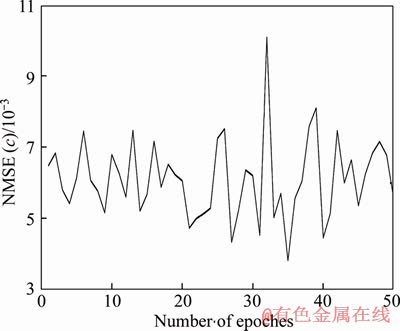
Figure 5 Monte Carlo comparison of true value with c

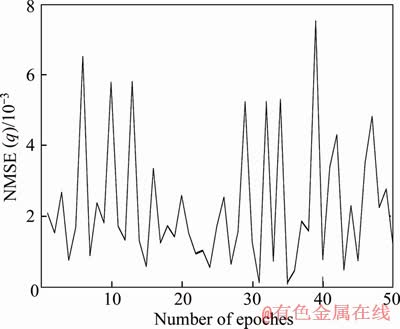
Figure 6 Monte Carlo comparison of true value with q

According to the Monte Carlo method described above, the simulation experiment results can achieve the expected tracking effect. The estimation of the Fourier coefficients can be pointed out. Figure 7 indicates the estimation of the Fourier coefficients for c by using Galerkin-based EKF with N=6, and Figure 8 indicates the estimation of the Fourier coefficients for q by using Galerkin-based EKF with N=6.

Through further simulation experiments, it can be found the number of Fourier coefficients is greater than 2, and the extra Fourier coefficients contribute to the estimation accuracy is actually invalid. Figures 9 and 10 show the simulation accuracy curves for two basis functions and six basis functions.

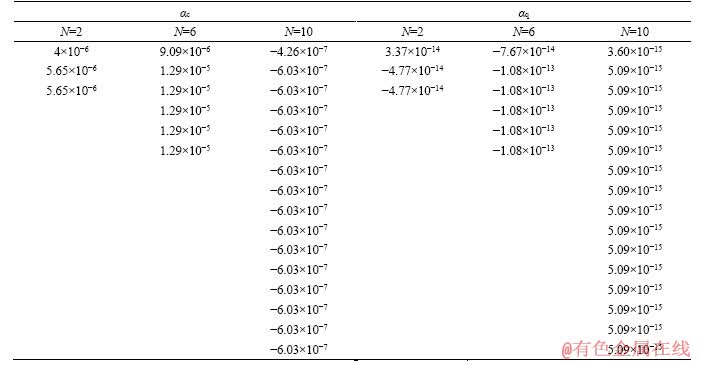
The reason is that we estimate the carbon dioxide concentration at the exit of the adsorption tower. From Eq. (18), we can see that except for the first basis function, which is 1/L, the other basis functions become 1 at Z=L, corresponding to Fourier coefficients all equal. The comparison is listed in Table 2.

6 Conclusions

Based on the particularity of carbon dioxide adsorption process, Galerkin method is used to solve the PDE equation in the adsorption model. By selecting a finite number of trial functions and superimposing them, the weighted integrals of the results on the solution domain and boundary are obtained to satisfy the original equations and a set of simple solutions are obtained. The theoretical analysis and simulation result confirmed the following conclusions:

1) Although the use of Galerkin method to solve the PDE equation will bring some errors, but the simulation results can still meet the requirements. According to the simulation experiment, the simulation adsorption curve can be well tracked during the whole adsorption process.

2) The results of many simulation experiments show that Galerkin-based EKF has good robustness and stability, and there is no divergence in the process of using Galerkin-based EKF.

3) The relationship between the number of basis functions and the estimation accuracy is weak. Therefore, in order to avoid dimensional disaster,an appropriate number of basis functions can be chosen to reduce the computational burden.

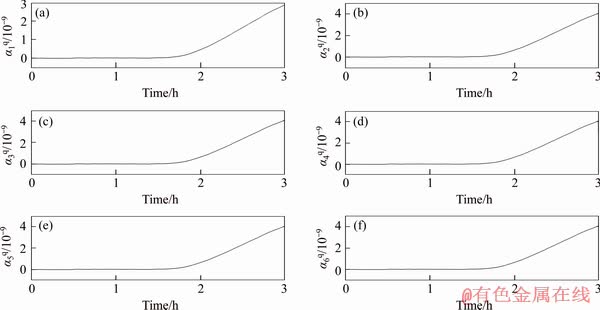
Figure 7 Estimation of Fourier coefficients for q by using Galerkin-based EKF with N=6

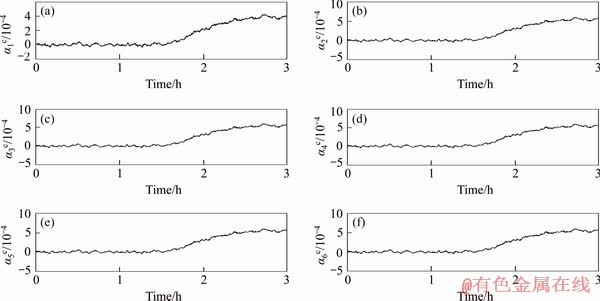
Figure 8 Estimation of Fourier coefficients for c by using Galerkin-based EKF with N=6

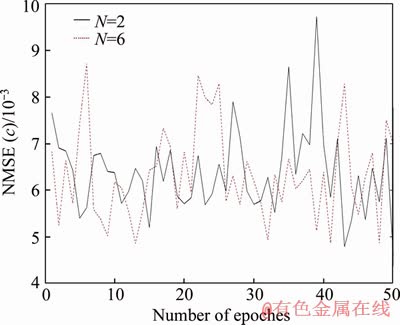
Figure 9 Estimation of Fourier coefficients for c by using Galerkin-based EKF with N=6

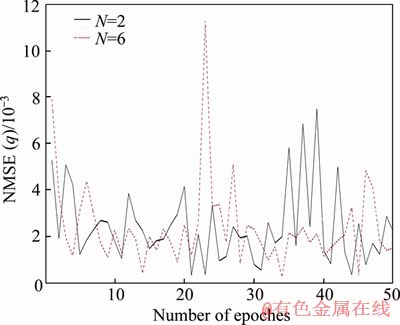
Figure 10 Estimation of Fourier coefficients for q by using Galerkin-based EKF with N=6

Table 2 Comparison of Fourier coefficients with different numbers of basic function

4) Through the use of the Galerkin-based EKF method in this paper, the status of the system can be displayed in real time, which provides an excellent method for the next step of system fault diagnosis.

References

[1] SHARMA G, RAI R N. Reliability modeling and analysis of environmental control and life support systems of space stations: A literature survey [J]. Acta Astronautica, 2019, 155(2): 238-246. DOI: 10.1016/j.actaastro.2018.12.010.

[2] JASON C, CAROL G, TRACY G. NASA’s exploration systems and habitation (X-Hab) academic innovation challenge [J]. Acta Astronautica, 2018, 151: 412-419. DOI: 10.1016/j.actaastro.2018.06.042.

[3] HAGER P, CZUPALLA M, WALTER U. A dynamic human water and electrolyte balance model for verification and optimization of life support systems in space flight applications [J]. Acta Astronautica, 2010, 67(9, 10): 1003-1024. DOI: 10.1016/j.actaastro.2010.06.001.

[4] GROGAN P T, YUE H K, de WECK O L. Space logistics modeling and simulation analysis using space net: Four application cases [C]// AIAA Space 2011 Conference and Exposition. Long Beach, California: AIAA Paper, 2011: 2011-7346. DOI: 10.2514/6.2011-7346.

[5] PERRY J, CARRASQUILLO R, HARRIS D. Atmosphere revitalization technology development for crewed space exploration [C]// 44th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA, 2006: 2120-2140. DOI: 10.2514/6.2006-140.

[6] JAMES J T, MACATANGAY A. Carbon dioxide our common “Enemy” [R]. NASA/Johnson Space Center, 2009.

[7] ZHU Y H, LUO Y Z. Multi-objective optimization and decision-making of space station logistics strategies [J]. International Journal of Systems Science, 2016, 47(13): 3132-3148. DOI: 10.1080/00207721.2015.1091898.

[8] LI Y, YUAN Y P, Li C F, HAN X, ZHAN X S. Human responses to high air temperature, relative humidity and carbon dioxide concentration in underground refuge chamber [J]. Building & Environment, 2018, 131: 53-62. DOI: 10.1016/ j.buildenv.2017.12.038.

[9] MAO T. Study on adsorption performance of solid amine carbon dioxide in crew cabin [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. (in Chinese)

[10] HU W, WU Q E, ZOU J H. Research on automatic fault diagnosis of environmental control and life support systems [J]. Journal of Comuptational and Theoretical Nanoscience, 2014, 11(5): 1394-1402. DOI: info:doi/10.1166/jctn.2014. 3509.

[11] ZHOU Jian-ping. A review of Tiangong-1/Shenzhou-8 rendezvous and docking mission [J]. Manned Spacecraft, 2012, 18(1): 1-5. DOI: 10.16329/j.cnki.zrht.2012.01.004. (in Chinese)

[12] WEN Hui. Tiangong-2 Space Laboratory achieved a number of “first” verifications [J]. Aerospace China, 2016(11): 4-7. (in Chinese)

[13] ZHOU Jian-ping. Chinese space station project overall vision [J]. Manned Spaceflight, 2013, 19(2): 1-10. (in Chinese)

[14] STAMBAUGH I, RODRIGUEZ B, VONAU W Jr, BORREGO M. Environmental control and life support system design for a space exploration vehicle [C]// 42nd International Conference on Environmental Systems. 2012. DOI: 10.2514/6.2012-3622.

[15] ANCA O, KOCAN K X, MEBANE D S, SCHMAL J P, BHATTACHARYYA D. Probabilistic model building with uncertainty quantification and propagation for a dynamic fixed bed CO₂ capture process [J]. Energy & Fuels 2020, 34(2): 2516-2532. DOI: 10.1021/ acs.energyfuels.9b03250.

[16] RONG A, PANG L P, LIU M, YANG D S. Muti-objective optimization for solid amine CO₂ removal assembly in manned spacecraft [J]. Entropy, 2017, 19(7): 348. DOI: 10.3390/e19070348.

[17] YANG Dong-sheng, LIU Meng, PANG Li-ping, YU Qing-ni, HUANG yong. Effect of H₂O on CO₂ removal performance of 5A molecular sieve of space station [J] Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1485-1491. DOI: 10.13700/ j.bh.1001-5965.2014.0580. (in Chinese)

[18] GUO R, LI Y H, LV M B. Design of infinite sliding mode state observer with application to CO₂ absorption system of space station [J]. Acta Astronautica, 2019, 161(5): 579-587. DOI: 10.1016/j.actaastro.2019.05.001.

[19] ZHAO J, MILI L, GOMEZ-EXPOSITO A. Constrained robust unscented Kalman filter for generalized dynamic state estimation [J]. IEEE Transactions on Power Systems, 2019, 34(5): 3637-3646. DOI: 10.1109/TPWRS.2019.2909000.

[20] PENG K, YIN X Y, YIN G Z, XU J, HUANG G, YIN Z Q. Galerkin solution of Winkler foundation-based irregular Kirchhoff plate model and its application in crown pillar optimization [J]. Journal of Central South University, 2016, 23(5): 1253-1263. DOI: 10.1007/s11771-016-0375-6.

[21] WIBOWO W K, JEONG S K. Improved estimation of rotor position for sensorless control of a PMSM based on a sliding mode observer [J]. Journal of Central South University, 2016, 23(7): 1643-1656. DOI: 10.1007/s11771- 016-3219-5.

[22] CHEN L H, SHI P, LIU M. Fault reconstruction for Markovian jump systems with iterative adaptive observer [J]. Automatica, 2019, 105: 254-263. DOI: 10.1016/j.automatica. 2019.03.008.

[23] LIU F, MA J, SU W X, CHEN H N, TIAN H X, LI Q C. SOC estimation based on data driven extended Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle [J]. Journal of Central South University, 2019, 26(6): 1402-1415. DOI: https://doi.org/10.1007/s11771- 019-4038-2.

[24] RAVI K D V A N, KOTESWARA R S, PADMA R K. A novel estimation algorithm for torpedo tracking in undersea environment [J]. Journal of Central South University, 2019, 26(3): 673-683. DOI: 10.1007/s11771-019-4038-2.

[25] SINGLETON R K, STRANGAS E G, AVIYENTE S. Extended Kalman filtering for remaining-useful-life estimation of bearings [J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1781-1790. DOI: 10.1109/tie.2014. 2336616.

[26] PANDAY A, BANSAL O, SRINIVASAN P. Thermoelectric modeling and online SOC estimation of Li-ion battery for plug-in hybrid electric vehicles [J]. Modelling and Simulation in Engineering, 2016, 16: 1-12. DOI: 10.1155/ 2016/2353521.

[27] FENG D S, FENG D S, WANG H H. An element- free Galerkin method for ground penetrating radar numerical simulation [J]. Journal of Central South University, 2015, 22(1): 261-269. DOI: 10.1007/s11771-015-2517-7.

[28] LIU J, TAVENER S, WANG Z. Lowest-order weak Galerkin finite element method for Darcy flow on convex polygonal meshes [J]. SIAM Journal on Scientific Computing B, 2018, 40(5): 1229-1252. DOI: 10.1137/17M1145677.

[29] WANG X J, LIN S, WANG S P, SHI J, ZHANG C. A multi-fault diagnosis strategy of electro hydraulic servo actuation system based on extended Kalman filter [C]// IEEE 8th International Conference on CIS & RAM. Ningbo, China, 2017: 614-619. DOI: 10.1109/ICCIS.2017.8274848.

[30] WANG Y, LEVAN M D. Adsorption equilibrium of carbon dioxide and water vapor on zeolites 5A and 13X and silica gel: Pure components [J]. Journal of Chemical & Engineering Data, 2009, 54(10): 2839-2844. DOI: 10.1021/je800900a.

[31] MULGUNDMATH V P, TEZEL F H, SAATCIOGLU T, GOLDEN C T. Adsorption and separation of CO₂/N₂ and CO₂/CH₄ by 13X zeolite [J]. The Canadian Journal of Chemical Engineering, 2012, 90(3): 730-738. DOI: 10.1002/ cjce.20592.

[32] WALTER W J, SMITH E H. Simulation and design models for adsorption processes [J]. Environ Sci Technol, 1987, 21(11): 1040-1050. DOI: 10.1021/ es00164a002.

(Edited by FANG Jing-hua)

中文导读

基于Galerkin的扩展卡尔曼滤波器及其在CO₂去除系统中的应用

摘要：二氧化碳去除系统是长期载人航天器中控制舱内CO₂浓度最关键的系统。为了确保舱内的CO₂浓度在可接受的范围内，需要实时估计CO₂去除系统的状态。本文首先建立实际系统的数学模型，再提出了基于Galerkin的扩展卡尔曼滤波算法，估计CO₂去除系统的状态。该方法采用Galerkin逼近法将偏微分方程转换为常微分方程，然后利用扩展卡尔曼滤波器进行状态估计。然后，以实际载人航天任务的实际工况为条件进行了仿真实验。仿真结果表明，该方法可以有效地估计系统状态，同时避免了尺寸爆炸的问题，并且对测量噪声具有很强的鲁棒性。因此，该方法也可以为CO₂去除系统的故障诊断和故障定位打下基础。

关键词：二氧化碳去除系统；Galerkin法；无限维非线性滤波器；扩展卡尔曼滤波器

Foundation item: Project (050403) supported by Pre-research Project in the Manned Space Filed of China

Received date: 2020-01-09; Accepted date: 2020-05-05

Corresponding author: LI Yun-hua,PhD,Professor;Tel:+86-10-82339038;E-mail:yhli@buaa.edu.cn;ORCID:0000-0001-6573-1267