基于多层剪枝的攻击特征自动提取方法
刘卫国，文碧望
(中南大学 信息科学与工程学院，湖南 长沙，410083)
摘要：针对现有攻击特征自动提取方法抗噪能力弱和准确性不高的问题，利用多层剪枝策略进行攻击特征自动提取。采用多层次架构使得各层间的序列比对相对独立，在同一时间可进行不同层次的多个双序列比对，从而提高计算效率。双序列比对使用改进的NLA算法，修改其相似度得分函数，对连续空位使用线性罚分，同时鼓励连续字符匹配，并用0代替得分为负的值且遇0时回溯，从而得到最优值。通过剪枝判据和置信区间辨别出噪声序列并保留，再与其他序列比对完成后生成的序列进行比对，进而判断剪枝，得到最终的序列比对结果，从而消除了结果中的部分噪声干扰。研究结果表明：该方法具有良好的抗噪能力，提取的攻击特征准确度更高。
关键词：入侵检测；攻击特征自动提取；序列比对；剪枝策略
中图分类号：TP393 文献标志码：A 文章编号：1672-7207(2014)10-3423-07
Approach for automatically generating attack signatures based on hierarchically pruning strategy
LIU Weiguo, WEN Biwang
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Aiming at the fact that current approaches for automatically generating attack signatures have problems in noise-tolerance and the accuracy of attack signatures, an approach based on hierarchically pruning strategy (HPS) was presented. Hierarchical structure made the pair-wise alignment between layers run independently and proceed at the same time to increase computational efficiency. The NLA (normalized local alignment) algorithm used in pair-wise alignment was improved by introducing encouraging function and linear punitory factor to adjust the scoring function, and the function replaced the negative score with the zero value and backtracked when it encountered the zero and thus the optimal value was obtained. The noise sequences were judged by the pruning criterion and confidence interval, and compared with the results of other sequence alignment to eliminate noise interference in the final result. The results show that this approach has better noise-tolerance and generates more accurate signatures.
Key words: intrusion detection; signature automatic generation; sequence alignment; pruning strategy
基于特征的入侵检测是应对网络蠕虫、病毒和恶意程序的有效方法。目前攻击特征主要靠事后人工分析，存在速度慢、费时长、难以应对变形攻击等问题[1]。为了能够自动、准确并快速地提取攻击特征，近年来许多研究者对攻击特征自动提取技术开展了研究。已有的攻击特征提取方法主要包括最长公共子串提取[2]、固定长度负载出现频率分析[3]、可变长度负载出现频率分析[4]、网络协议的状态自动机[5]、可回溯动态污点分析[6]、多序列比对[7]等。其中，基于多序列比对的方法因为能够提取长度很短的特征片段并且能够挖掘特征片段之间的距离限制关系，是目前特征提取准确性较高的方法之一。Needleman-Wunsch算法[8]和Smith-Waterman算法[9]是具有代表性的双序列比对算法。Needleman-Wunsch算法基于动态规划思想，通过计算2个序列的相似度得分，构造相似度矩阵，并动态回溯寻找最优比对结果，但Needleman-Wunsch算法易产生碎片[10]。Smith-Waterman算法对Needleman-Wunsch算法进行了改进，用局部比对代替全局比对，提高了比对结果的准确性。但Smith- Waterman算法存在马赛克效应和阴影效应[11-12]，Arslan等[11]提出一种利用长度标准化得分函数的NLA(Normalized Local Alignment)算法来消除这2个效应，得到具有最大相似度的比对结果。霍红卫等[13]使用最大权值路径算法来优化相似度得分值。秦拯等[14]针对Needleman-Wunsch算法缺乏攻击知识积累的问题，提出了基于知识积累的序列比对方法IASA，有效地保留了比对过程中具有语义信息的片段，使比对结果趋于合理。唐勇等[15]提出了一种多序列比方法HMSA，在保证特征准确性的基础上，通过在渐进比对过程中加入剪枝机制来消除噪声的影响，其优点是特征提取准确性高，但如果某些攻击的特征本身就满足该方法的剪枝条件，那么会把正确的特征剪枝掉。本文作者通过层次迭代，并在层次之间采用改进的双序列比对算法进行序列比对，在层次比对的结果中通过噪声判据和置信区间来剪去噪声序列，消除噪声干扰，从而得到更精确的攻击特征。
1 方法描述
1.1 基本框架
在攻击特征自动提取中，通常都是采用在双序列比对过程逐步加入新的序列，直到所有序列都加入完毕的渐近式结构。本文运用多层次架构，在同一层或不同层中的双序列比对独立进行，这不同于渐近式结构的逐步添加，多层次架构可以同时进行多个双序列比对，从而提高比对效率。一个包含6层比对的结构框架如图1所示。
在图1中，第1层中根据层次引导树排列相似度得分最高的9对双序列进行比对，比对结果通过剪枝判据判断剪枝。第2对双序列比对结果通过剪枝判据被判断为噪声，从而被剪枝，第9对双序列比对结果被判断为正常样本序列。在第2层及以上通过置信区间保留噪声序列，将保留序列与其他序列比对结果进行比对，判断剪枝从而剪去噪声。图1中第2层有4对双序列比对，第4对比对结果不在置信区间，从而将原序列保留。其他序列在第5层中得到的比对结果，再与保留序列进行双序列比对，结果通过剪枝判据判断剪枝，进而得到最终对比结果。该方法主要由4个部分组成。
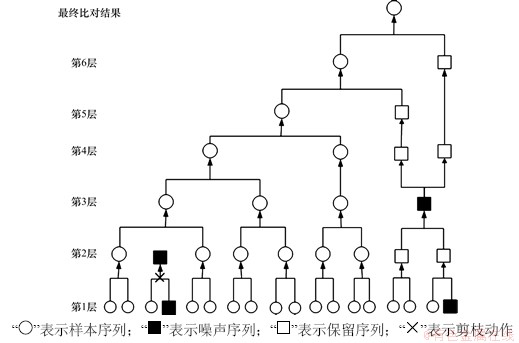
图1 方法结构框架图
Fig. 1 Structural framework
1) 双序列比对。对n个序列中任意2个序列运用改进后的NLA算法进行双序列比对，得到n(n-1)/2个比对的结果，将结果中所有的字符匹配保存到字符匹配库中，并通过2个序列之间的相似度值构造序列之间的距离矩阵。
2) 构造层次引导树。基于第1)步中得到的距离矩阵通过邻近归并法构造层次引导树。该层次引导树中保存了每个序列所处的层次，并指明了在下一步的比对过程中，每次选择哪2个序列或比对结果进行比对。比对优先选择处于同一层次的序列，若某序列在同一层次中没有可比对序列，则将此序列层次加1，序列上移一层。
3) 运用剪枝策略得到对比结果。在第1层中对双序列比对后的结果进行判断，如果不符合剪枝判据，则剪枝。在第2层及以上的双序列比对结果进行置信区间判断，相似度低于阈值(即不在置信区间内)的比对结果被认为是噪声序列，但不被剪枝，而是将2个序列保留，待其他比对全部结束后再与生成的特征序列一一进行比对，若符合判据则比对结果作为新的特征序列，否则就剪枝，仍保持原特征序列。
4) 根据层次引导树通过一系列的双序列比对分层次完成多序列比对。
1.2 双序列比对改进算法
双序列比对是多序列比对的基础。在攻击特征自动提取中，获取局部的有语义的连续符号串比全局比对获得大量碎片更具有实际意义，为获取连续的、少碎片的攻击特征，下面对NLA算法进行改进。
1) 改进算法的基本思想
对于给定的比对序列X和Y，构造相似度矩阵，令m是单个字符匹配得分，d是单个字符不匹配得分，z是单个空位罚分，Wm是字符匹配得分，Wd是不匹配得分，δ是空位罚分，h为匹配字符数，k为不匹配字符数，g为空位的数目。其中Wm=hm，Wd=kd，通常相似度得分S=Wm+Wd+δ。
NLA算法通过将得到的子序列比对的相似度得分S用它们的长度进行标准化，回溯查找高相似度特征串，算法原理包括以下2个方面：
① 使用定义好的相似度得分函数计算出进行比对的2个序列的所有可能的相似性得分值，以打分矩阵的形式存储，打分矩阵记为M，打分矩阵元素分值记为SNLA，打分矩阵回溯方向记为PTR。SNLA的计算公式为：
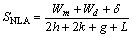(1)
其中：L为长度修正系数(常量)。
② 在计算得到的打分矩阵中，回溯寻找最优相似度得分。
当出现连续g′个空位时，NLA算法的空位罚分δ=g′z。现对算法进行改进，为减少连续空位对得分函数的影响，对首先出现的空位罚分记为p，当出现连续g'个空位时，空位罚分δ′=p+( g′-1)z(p＞＞z)，同时为了鼓励连续匹配字符，对于多个连续匹配的字符引进鼓励函数e(S)来增加匹配得分，其中S为连续匹配字符的相似度得分。同时在相似度矩阵中，得分为负值的都用0替代，在计算最优双序列比对时遇0则回溯。于是序列比对得分函数为：
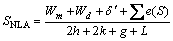(2)
其中：S为序列X和Y比对结果中的片段。
2) 算法描述
输入：序列X和序列Y。
输出：比对结果序列R，相似度值SC。
参数：N为X的长度；M为Y的长度；Si,j表示最优相似度得分；
表示经长度标准化后的相似度得分；Ti,j表示当前相似度得分，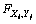
表示字母之间的相似度得分；PTR表示回溯指针；Lm 表示子序列中匹配字符数；Ld表示子序列中不匹配字符数；Lz表示子序列中空位的数目。
初始化：
for i=1 to N do
Si,0 = 0；Ti,0 = 0；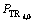
=UP；
end
for j=1 to M do
S0,j= 0；T0,j= 0；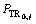
=LEFT；
end
S0,0=0；T0,0=0；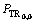
=STOP；
迭代：
for i=1 to N do
for j=1 to M do
if Xi，Yj不是通配符 and Xi = Yj then
；
；
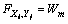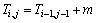else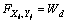 
；
；
；
；
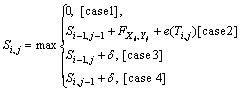
end
end
回溯：
分配一个空序列R；
while 所有矩阵元素SNLA不等于0 do
if(该矩阵元素的SNLA最大且不为0){
分配一个新的字符r并将之加到序列R的头部；
switch PTR do
case STOP：；
case DIAL：r = Xi；i = i－1；j = j－1；
case UP：r =‘*’；i = i－1；
case LEFT：r =‘*’；j = j－1；
}else 将已回溯过的SNLA置为0；
end
return R，SC=SＮ,Ｍ。
1.3 剪枝策略
在层次序列比对中，为了避免噪声序列与正常序列比对的结果被认为是无意义的特征而被剔除，最终可能导致整个层次比对没有结果输出的情况，每一次进行双序列比对后的结果都要进行剪枝。剪枝的作用是及时去掉平凡解，以提高方法的收敛速度，并使方法可以抵抗噪声的干扰。
在构造完引导树后，采用分层迭代方法，每次选择距离最近的2条序列对进行双序列比对，在新的一层得到新的序列，比对结果要按照剪枝判据和置信区间判断剪枝。有研究表明：数据流中包含了3个关键片段，而且长度≥3的字符串可以有效地描述特征片段[15-17]，因此本文以“比对结果中片段的数目≥3，并且有2个片段的长度≥3”作为剪枝判据。剪枝策略如图2所示。
在第1层比对中，若比对结果符合剪枝判据则进入高一层，不符合则被剪枝。在图2中，3号和4号序列比对结果不符合判据被剪枝。在第2层及以上层，利用比对相似度估计修改剪枝策略，使相似度低于阈值的比对不被剪枝，而是将2个序列搁置，待其他比对全部结束后再与生成的特征序列一一进行比对，若符合判据则比对结果作为新的特征序列，否则剪枝保留序列，保持原特征序列。
过程描述如下：
输入：序列集合S。
输出：多序列比对结果。
参数：R为S中的序列在双序列比对后相似度值集合，W为保留集合，Tn为比对结果集合，n为序列层次。
初始化：R＝S，W＝{}，T＝{}，n=1。
第1阶段迭代 n=1:
while |R|>0 do
if |R| = 1,即R中只有序列S then
将S加入Tn+1；
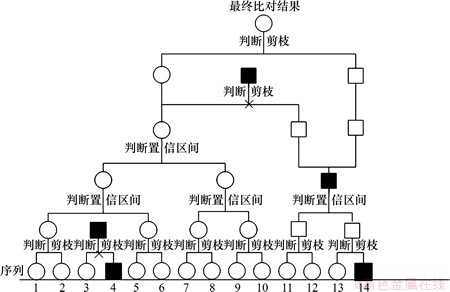
图2 剪枝策略图
Fig. 2 Chart of pruning policy
else 从R中选取相似度最大的序列Si和Sj，运用改进序列比对算法得到结果
；
判断剪枝：
if 中片段的数目≥3并且有两个片段的长度≥3 then
将加入Tn+1；
else 剪枝
end
第2阶段迭代 n+1＞1:
while |Tn+1|≠1 do
n=n+1;
while |Tn|＞0 do
if |Tn|=1即Tn中只有序列S then
将S加入Tn+1;
else 从Tn中选取相似度最大的序列Si和Sj，运用改进序列比对算法得到结果；
判断剪枝：
if 在置信区间内 then
加入Tn+1;
else 将Si和Sj加入W；
end
end
第3阶段迭代 |Tn+1|=1:
while |W|≠1 do
从W中依次取出序列SW，与Tn+1里的唯一序列ST，运用改进序列比对算法得到结果
；
判断剪枝：
if 中片段的数目≥3并且有2个片段的长度≥3 then
Tn+1＝{}，将加入Tn+1；
else 剪枝，在W中删除SW；
end
结束：输出Tn+1。
2 实验分析
2.1 方法有效性验证
选取Apache-Knacker和CodeRed Ⅱ 2种攻击，利用病毒变形引擎进行变形处理，使每种攻击产生100个攻击样本，此外，在KDD99数据集中(不包含攻击数据)选取15 000个数据报用于检测误报率和漏报率。选取HMSA、IASA和本文方法HPS分析各自的自动提取攻击特征能力，以及误报率、漏报率，并且对实验的结果进行对比分析。其中误报率为正常样本被误报为异常的样本数与正常样本总数之比，漏报率为未被检测出来的异常数据样本数与异常样本总数之比。
实验中参数设置如下：匹配得分取值为1，不匹配得分取值为-0.5，空位罚分取值为-1。第一次空位罚分取值为-1，出现连续的其他空位取值-0.02。对于连续匹配字符的相似度得分S，连续匹配奖励函数为：
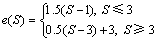(3)
表1和表2所示分别为3种方法对Apache-Knacker和CodeRed Ⅱ 2种攻击所生成的攻击特征以及将这些攻击特征用于入侵检测时的误报率和漏报率。
表1 对Apache-Knacker类攻击的实验结果
Table 1 Experimental result of attack Apache-Knacker category
表2 对CodeRed II类攻击的实验结果
Table 2 Experimental result of attack CodeRed II category
从表1和表2可以看出：HMSA、IASA和HPS对2种攻击的漏报率都为0，从而说明了方法所产生的攻击特征是准确的。从误报率上来说，使用本文方法的提取结果，误报率都要比其他2种方法的低，因此说明使用本文提出的攻击特征提取方法，提取的攻击特征准确率更高，对变形攻击的检测效果更好。
2.2 抗噪能力测试
对HMSA和HPS进行抗噪能力测试。在理想情况下，满足以下2个假设：
1) 任意2个噪声比对都会产生平凡解而被剪枝。
2) 任意2个样本比对都不会被剪枝，并且可以产生准确的攻击特征。
随机产生一系列的字符串作为噪声，固定使用50个样本，通过逐步增加随机生成噪声的数量，来测试与比较在不同信噪比下2种方法在返回结果和返回正确结果方面的表现，其中返回正确结果是指生成的攻击特征在对该次实验样本集(包括50个攻击样本及随机插入的噪声)的检测中漏报率为0。
图3所示为2种方法在多次测试中成功返回结果的概率，图4所示为2种方法在多次测试中返回正确结果的概率。由图3和图4可见：当噪声数/样本数≤1时，2种方法都具有较强的抗噪声能力；但当噪声数/样本数＞1时，本文方法的抗噪声能力则要明显比HMSA方法的优。
当样本序列和噪声序列进行比对时，比对结果可能是样本序列，也可能是噪声序列，HMSA方法在这种情况下，或在没有满足理想情况的假设1下，会导致噪声之间比对后没有被剪枝掉，从而与样本之间的比对结果进行比对，导致没有结果返回。而在本文方法中，即使噪声之间和噪声与样本之间的比对结果没有被剪枝，也会因为没有进入置信区间而被搁置，待其他比对全部结束后再与生成的特征序列一一进行比对，若不符合剪枝条件则比对结果作为新的特征序列，否则仍保持原特征序列，这样大大降低了因为噪声的干扰而没有结果返回的概率。
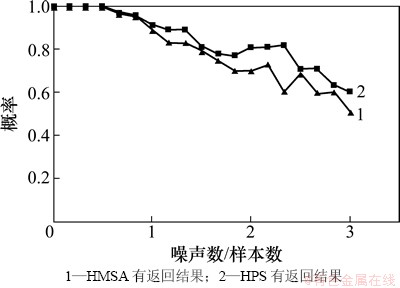
图3 IISPrinter攻击的抗噪能力实验结果1
Fig. 3 Experimental result 1 of IISPrinter on noise-tolerant ability
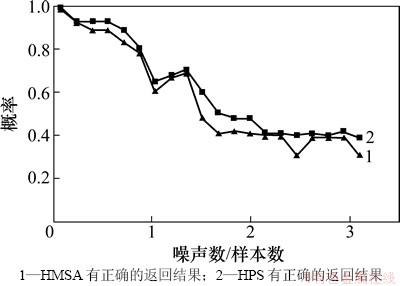
图4 IISPrinter攻击的抗噪声能力实验结果2
Fig. 4 Experimental result 2 of IISPrinter on noise-tolerant ability
3 结论
1) 运用多层序列比对架构，在每一层中都是相似度最大的2个序列进行比对，从而得到最优比对结果，同时层次间各个双序列比对各自相对独立同时进行，进而加快方法的收敛速度。
2) 改进双序列比对NLA算法的相似度得分函数，削弱了空位的影响并鼓励连续字符匹配，可以减少碎片数量，获取更多有语义的连续符号串，从而得到更少碎片且更加精确的攻击特征。
3) 在不同层次中用不同的剪枝判断方法，在第一层中通过剪枝判据判断剪枝，在其他层通过判断置信区间来剪去多余的噪声序列分枝，从而可以有效抵抗噪声的干扰。
4) 与其他特征提取方法相比，本文方法提取的攻击特征用于入侵检测时误报率和漏报率更低，且具有良好的精确度和抗噪性，是构建实际入侵检测系统时值得考虑的方法。
参考文献：
[1] 唐勇, 魏书宁, 胡华平. 抗噪的攻击特征自动提取方法[J]. 通信学报, 2009, 30(12): 124-130.
TANG Yong, WEI Shuning, HU Huaping. Noise-tolerant approach for automatically generating signatures of network attacks[J]. Journal on Communications, 2009, 30(12): 124-130.
[2] Kreibich C, Crowcroft J. Honeycomb-creating intrusion detection signatures using honeypots[J]. Computer Communication Review, 2004, 34(1): 51-56.
[3] Kim H A, Karp B. Autograph: toward automated, distributed worm signature detection[C]//Proceedings of the 13th USENIX Security Symposium. San Diego, CA: Proceedings of the 13th USENIX Security Symposium, 2004: 271-286.
[4] Li Z, Sanghi M, Chen Y, et al. Hamsa: fast signature generation for zero-day polymorphic worms with provable attack resilience[C]//Proceedings of IEEE Symposium on Security and Privacy. Washington DC, USA: IEEE Computer Society, 2006: 32-47.
[5] Yegneswaran V, Giffin J T, Barford P, et al. An architecture for generating semantics-aware signatures[C]//Proceedings of the 14th USENIX Security Symposium. Baltimore, MD: Proceedings of the 14th USENIX Security Symposium, 2005: 97-112.
[6] 刘豫, 聂眉宁, 苏璞睿. 基于可回溯动态污点分析的攻击特征生成方法[J]. 通信学报, 2012, 33(5): 21-29.
LIU Yu, NIE Meining, SU Purui. Attack signature generation by traceable dynamic taint analysis[J]. Journal on Communications, 2012, 33(5): 21-29.
[7] 邹权, 郭茂祖. 多序列比对算法的研究进展[J]. 生物信息学, 2010, 8(4): 311-317.
ZOU Quan, GUO Maozu. Development of multiple sequence alignment algorithms[J]. China Journal of Bioinformatics, 2010, 8(4): 311-317.
[8] Needleman S B, Wunsch C D. A general method applicable to the search for similarities in the amino acid sequence of two Proteins[J]. Journal of Molecular Biology, 1970, 48(3): 443-453.
[9] Smith T F, Waterman M S. Identification of common molecular subsequences[J]. Journal of Molecular Biology, 1981, 147(1): 195-197.
[10] Newsome J, Karp B, Song D. Polygraph: Automatically generating signatures for polymorphic worms[C]//Proceedings of the 2005 IEEE Symposium on Security and Privacy. California, CA: IEEE Computer Society, 2005: 226-241.
[11] Arslan A N, Egecioglu O, Pevzner P A. A new approach to sequence comparison: normalized sequence alignment[J]. Bioinformatics, 2001, 17(4): 327-337.
[12] 赵旭, 何聚厚. 基于NLA的Polymorphic蠕虫特征自动提取算法研究[J]. 计算机工程与应用, 2012, 48(8): 122-124.
ZHAO Xu, HE Juhou. Automatic signature generation research for Polymorphic worm based on NLA algorithm. Computer Engineering and Applications, 2012, 48(8): 122-124.
[13] 霍红卫, 肖智伟. 基于最大权值路径算法的DNA多序列比对方法[J]. 软件学报, 2007, 18(2): 185-195.
HUO Hongwei, XIAO Zhiwei. A multiple alignment approach for DNA sequences based on the maximum weighted path algorithms. Journal of Software, 2007, 18(2): 185-195.
[14] 秦拯, 尹毅, 陈飞杨, 等. 基于序列比对的攻击特征自动提取方法[J]. 湖南大学学报(自然科学版), 2008, 35(6): 77-80.
QIN Zheng, YIN Yi, CHEN Feiyang, et al. Automatic generation of attack signatures based on sequence alignment[J]. Journal of Hunan University(Natural Sciences), 2008, 35(6): 77-80.
[15] 唐勇, 卢锡城, 胡华平, 等, 基于多序列联配的攻击特征自动提取技术研究[J]. 计算机学报, 2006, 29(9): 1533-1541.
TANG Yong, LU Xichen, HU Huaping, et al. Automatic generation of attack signatures based on sequence alignment[J]. Chinese Journal of Computers, 2006, 29(9): 1533-1541.
[16] Crandall J R, Wu S F, Cong F T. Experiences using Minos as a tool for capturing and analyzing novel worms for unknown vulnerabilities[C]//Procedings of the 2nd International Conference on Detection of Intrusions and Malware and Vulnerability Assessment(DIMVA 2005). Berlin, BRD: Springer Berlin Heidelberg, 2005: 32-50.
[17] Crandall J R, SU Zhendong, Wu S F, et al. On deriving unknown vulnerabilities from zero-day polymorphic and metamorphic worm exploits[C]// Proceedings of the 12th ACM Conference on Computer and Communications Security. New York, USA: The Association for Computing Machinery, 2005: 235-248.
(编辑 杨幼平)
收稿日期：2013-10-16；修回日期：2013-12-11
基金项目(Foundation item)：国家自然科学基金资助项目(61073187)(Project (61073187) supported by National Natural Science Foundation of China)
通信作者：刘卫国(1963-)，男，湖南祁阳人，博士，教授，从事网络与信息安全、智能信息处理研究；电话：0731-88830062；E-mail：liuwg@csu.edu.cn
