J. Cent. South Univ. Technol. (2011) 18: 473-478

DOI: 10.1007/s11771-011-0720-8

Design of decoupling Smith control for multivariable system with time delays

HUANG Can(黄灿), GUI Wei-hua(桂卫华), YANG Chun-hua(阳春华), XIE Yong-fang(谢永芳)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: In order to solve the decoupling control problem of multivariable system with time delays, a new decoupling Smith control method for multivariable system with time delays was proposed. Firstly, the decoupler based on the adjoint matrix of the multivariable system model with time delays was introduced, and the decoupled models were reduced to first-order plus time delay models by analyzing the amplitude-frequency and phase-frequency characteristics. Secondly, according to the closed-loop characteristic equation of Smith predictor structure, proportion integration (PI) controllers were designed following the principle of pole assignment for Butterworth filter. Finally, using small-gain theorem and Nyquist stability criterion, sufficient and necessary conditions for robust stability were analyzed with multiplicative uncertainties, which could be encountered frequently in practice. The result shows that the method proposed has superiority for response speed and load disturbance rejection performance.

Key words: multivariable process; time delay; Smith predictor; decoupling; robust stability

1 Introduction

Effective control of multivariable system with time delays processes is a difficult issue in the context of process control [1]. Input-output loops in a multivariable plant usually have different time delays, and for a particular loop its output could be affected by all the inputs through different time delays. Such a plant can be represented by a multivariable transfer function matrix with multiple time delays around an operating point. The researches of control method for this kind of multivariable plants with multiple time delays have received considerable attention [2-4].

For multivariable coupling system, the controller was designed for each sub-loop by analyzing the dominant pole and amplitude ratio by LUYBEN [5] and JIETAE and THOMAD [6]. This method led to a large number of controller design, and the controller regulating of one loop affected the other loops, even the performance of the system. Decoupling control is an effective method for multivariable system to eliminate the interactions of sub-loops. By decomposing the system to independent sub-loops, the controller is designed based on independent sub-loop. ASTROM et al [7] and SAEED et al [8] introduced static decoupler and dynamic decoupler at the input port to construct unit feedback closed-loop decoupling control. But the above method can be used only in two-input two-output process. It cannot be extended to the processes with more inputs and outputs. WANG et al [9] and SHEN et al [10] devised the expected diagonalization transfer matrix for the closed-loop control system, and proposed the realizable decoupler matrix by matching nominal system transfer matrix. Since the form of transfer matrix was set, the calculation of decoupler was complicated, and the structure of decoupler was too complex to implement. Therefore, it is necessary to do more researches on decoupling control for multivariable systems.

For single-input single-output processes with delay, Smith suggested a compensation scheme, which can remove the delay from the closed-loop characteristic equation and thus eases feedback control design and improves set-point response greatly [11]. This controller was extended to multivariable systems with multiple time delays [12-14]. Decoupler was introduced to eliminate the system coupling, and the controller was derived using the design method of single variable Smith controller by WANG et al [14]. So multivariable Smith decoupling is simplified to single variable Smith predictor design. It is a useful way to solve the problem of multivariable system with multiple time delays.

In this work, a new approach to the multivariable Smith predictor controller design was proposed for decoupling and stabilizing of multivariable process with multiple time delays. A decoupler was first introduced based on the adjoint matrix of the multivariable system model with time delays. To achieve better performance, additional delay items were added to diagonal elements of the decoupler matrix. With this decoupler, the multivariable Smith predictor controller was simplified to multiple single-loop Smith predictor controller design. After reducing the decoupled single-loop models to first-order plus time delay (FOPDT) models, PI controllers were designed by using the poles assignment rule of Butterworth filter.

2 Design of decoupling Smith control

The multivariable Smith predictor control structure is shown in Fig.1, where R(s), Y(s), C(s) and K(s) represent the input, output, controller, and decoupler, respectively. G(s) represents the process which is a stable nonsingular matrix, i.e., det(G(0))≠0. H(s)=G(s)K(s), H₀(s) is the same as H(s) except with no delays.

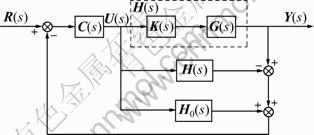
Fig.1 Multivariable Smith predictor structure

Consider the multivariable system with the transfer matrix:

where 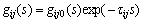 (i, j=1, …, n), represents the transfer function from i-th input to j-th output, g_ij0(s) represents strictly proper, stable scalar rational function, and τ_ij represents the time delay associated with g_ij(s). When the model is ideal, i.e., the process and its model is matched, the closed-loop transfer function from R(s) to Y(s) in Fig.1 becomes

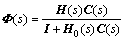                        (1)

2.1 Design of decoupler

Decoupling is to diagonalize the system transfer function G(s) to H(s), where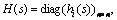 i=1, 2, …n, and h_i(s) represents regular rational transfer function. In this work, A×adj(A)=adj(A)×A=det(A)×I is used to design the decoupler as

K′=adj(G)

In order to include less delay terms, K′ multiplies time delay matrix as

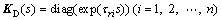
where τ_ri is the smallest time delay in each column of K′.

For the revised decoupler without time delays prediction terms, the design can be realized. Then the decoupler coefficient is modified in order to calculate conveniently, and the decoupler is shown as

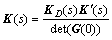                          (2)

So the decoupled process is

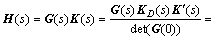
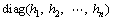                      (3)

2.2 Model reduction

After decoupling, the interactions were eliminated so that the system was equivalent to sub-loops existing independently. To simplify the decoupled process and ensure a good control system performance, model reduction was introduced to each sub-loop of the decoupled process.

Approximation of high order processes by low order plus dead time models is a common practice. As most industrial processes are inertial and time delays processes, which can be described by FOPDT models, the decoupled processes were reduced to FOPDT models in this work. The FOPDT model often reasonably describes the process gain, overall time constant and effective dead time of such a process. In order to find an approximation FOPDT model for h_i(s), three unknown parameters, namely k_i, τ_di and T_i (i=1, 2, …, n) should be determined:

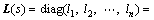
       (4)

Fitting Nyquist plots of high order a low order models at particular points, Eq.(5) is suggested to calculate the values of k_i, τ_di and T_i. This equation indicates that the steady state gain and gain margin are the same for the high order process and FOPDT model:

                    (5)

where the crossover frequency ω_xi of the original system is determined using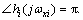

As a result, the parameters of the FOPDT model can be calculated using

k_i=h_i(0)                                     (6)

                        (7)

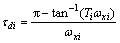                         (8)

Define that the matrix L₀(s) represents the reduced model matrix L(s) except with no delays,

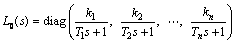        (9)

and then Eq.(1) is described as

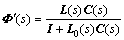                        (10)

2.3 Design of PI controller

In order to design a set of PI tuning formulae for a FOPDT model, the PI parameters K_Pi, T_Ii (i=1, 2, …, n) should be defined:

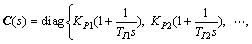
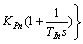                                               (11)

The Smith predictor in which a compensator is introduced can remove the delay from the closed-loop characteristic equation. It can be seen from the closed-loop transfer function characteristic equation of FOPDT model as

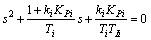                    (12)

The principle of Butterworth filter is poles assignment on unit circle symmetrically in the left half of complex plane by using real axis as symmetry axis [15]. In this case, the poles distribute uniformly on the Butterworth circle. For the ideal pole positions, Butterworth filter has the performance of low pass filter. The Butterworth filter is defined as

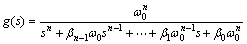
According to the principle of Butterworth, the expected transfer function characteristic equation for second-order system was designed. Distributing the poles on the position of the angle θ=45° to imaginary axis, the coefficient can be determined by β₀=1.000 and β₁=1.414. The parameters of PI controller are determined as

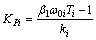                            (13)

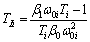                             (14)

where ω_0i is the cut-off frequency.

3 Robust stability analysis

The standard structure of system uncertainty is shown in Fig.2. M represents system model, which usually can not represent the actual process exactly in the real world and Δ represents any element of system uncertainty that is stable. According to the equivalence relation of small-gain theorem and Nyquist stability criterion, the system will be robustly stable, if and only if the spectrum radius satisfies the following condition [16-17]:

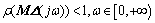
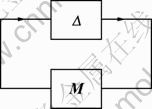
Fig.2 M-Δ standard structure

In practical engineering, many uncertainties can be described by multiplicative uncertainties, such as perturbation of process parameters, output uncertainties of operator, the uncertainties of sensors measured values. Defining Δ_i as multiplicative input uncertainties, Δ_o as multiplicative output uncertainties, the nominal system M_input and M_output from Δ_i and Δ_o to output of the multivariable system in Fig.1 is described by

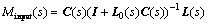
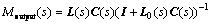
Then the necessary and sufficient condition of robustly stable for multivariable system with multiple time delays in Fig.1 is

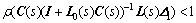             (15)

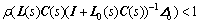            (16)

Correspondingly, the spectrum stability constrains shown in Eqs.(15) and (16) can be checked graphically by observing whether the magnitude plots of the left sides of Eqs.(15) and (16) fall below the unity for all ω[0, +∞).

4 Simulation

In order to show the effectiveness of the proposed design method, the following system is considered:

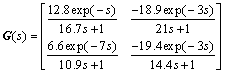
The decoupler is designed using Eq.(2):

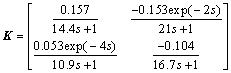
After revising the time delays and the coefficient, the decoupled processes are expressed as

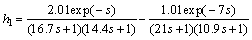
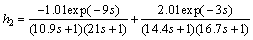
Reducing the decoupled system model, the cut-off frequencies of h₁(s) and h₂(s) are ω_x1=0.45 rad/s and ω_x2= 0.29 rad/s, respectively. According to Eqs.(6), (7) and  (8), the parameters of FOPDT models are calculated as  k₁=1, k₂=1, T₁=26.98, T₂=31.16, τ_d1=3.6 and τ_d2=5.8. So the reduced multivariable transfer matrix is

Fig.3 shows the Nyquist plots of the elements of h₁(s) and h₂(s), and their FOPDT approximation models l₁(s) and l₂(s). The Nyquist plot of reduced model and process model match approximately at low frequency, so the model reduction is effective.

Using Eqs.(13) and (14), the parameters of PI controller are

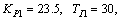
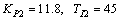
Then the PI controllers are determined as

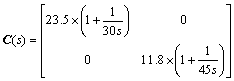
Output responses to unit step function in the first input r₁ and second input r₂ are shown in Fig.4. For the simulation, a 0.2 step disturbance has been applied to the process input at t=50 s. It is clearly seen that there is no overshoot in the setpoint responses by using the proposed method, and the process output responses are almost decoupled from each other. Moreover, obviously improved response speed and load disturbance rejection performance compared with those of WANG’s method are obtained.

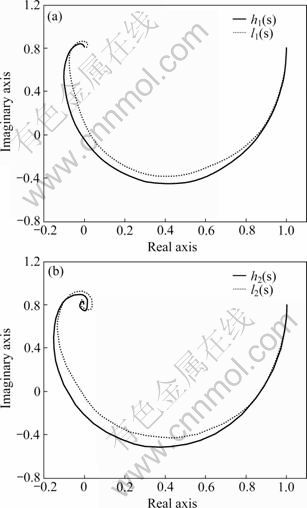
Fig.3 Nyquist plots of h₁(s) and l₁(s) (a) and h₂(s) and l₂(s) (b)

In order to further test the robust stability of the system, multiplicative input uncertainties Δ_i= diag{(s+0.2)/(2s+1), (s+0.2)/(2s+1)} and multiplicative output uncertainties Δ_o=diag{(s+0.3)/(s+1), (s+0.3)/(s+1)} were supposed in the simulation. According to the robust stability analysis given in section 3, the magnitude plots of spectral radius for uncertainties Δ_o and Δ_i are shown in Fig.5. It can be seen that both of the peak values are much less than the unity, indicating that the proposed control system facilitates good robust stability.

5 Conclusions

1) A new multivariable Smith predictor scheme for decoupling and stabilizing multivariable processes with multiple time delay is proposed, which can be used for high-dimensional processes.

2) With the adjoint matrix approach to the decoupler design and the model reduction of the decoupled process, the multivariable Smith predictor design is simplified to multiple single-loop Smith predictor design.

3) Based on the pole assignment of Butterworth filter, the PI controller for each decoupled loop is designed. Robust stability analysis is presented using the equivalence relation of small-gain theorem and Nyquist stability criterion. The spectrum stability constrains can be checked graphically by observing the magnitude plots of spectral radius. Numerical example shows that the approach has significant performance improvement over the existing methods.

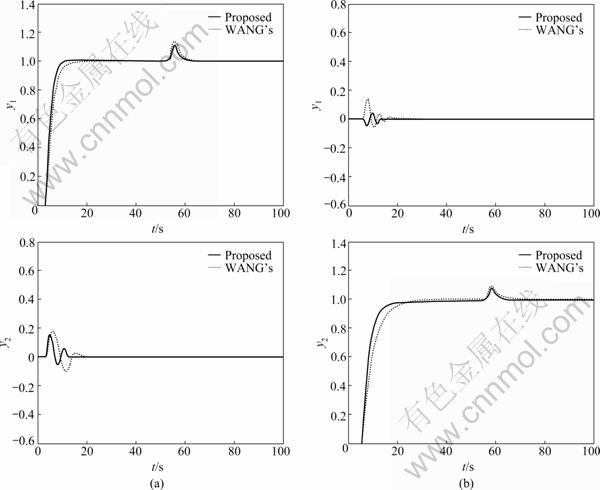
Fig.4 Output responses to unit step: (a) In r₁; (b) In r₂

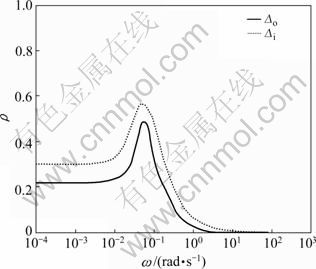
Fig.5 Spectral radius curve of system considered under multiplicative input and output uncertainties

References

[1] MIHAI H, WILLIAM A G, GUY A D. Time delay integrating systems: A challenge for process control industries [J]. A Practical Solution, Control Engineering Practice, 2002, 10(11): 1153-1161.

[2] DOMINIQUE N G, PATRICK L, ALAIN O. Robust control design for multivariable plants with time-delays [J]. Chemical Engineering Journal, 2009, 146(3): 414-427.

[3] DANIEL R S, JORGE J C, FRANCIS J D. A variable time delay compensator for multivariable linear processes [J]. Journal of Process Control, 2005, 15(2): 215-222.

[4] LIU Tao, ZHANG Wei-dong, GU Dan-ying, CAI Yun-ze. Research progress of frequency domain decoupling control design for chemical and industrial multivariable processes with time delays [J]. Acta Automatica Sinica, 2006, 32(1): 73-83. (in Chinese)

[5] LUYBEN W L. Simple method for tuning SISO controllers in multivariable system [J]. Industrial and Engineering Chemistry Process Design and Development, 1986, 25(3): 654-660.

[6] JIETAE L, THOMAD F E. Multiloop PI/PID control system improvement via adjusting the dominant pole or the peal amplitude ratio [J]. Chemical Engineering Science, 2006, 61(5): 1658-1666.

[7] ASTROM K J, JOHANSSON K H, WANG Qing-guo. Design of decoupled PI controllers for two-by-two systems [J]. IEE Proceeding Control Theory & Applications, 2002, 149(1): 74-81.

[8] SAEED T, IAN G, PETER J F. Tuning of decentralized PI (PID) controllers for TITO processes [J]. Control Systems Engineering, 2006, 14(9): 1069-1080.

[9] WANG Qing-guo, ZHANG Yu, CHIU Min-Sen. Decoupling internal model control for multivariable systems with multiple time delays [J]. Chemical Engineering Science, 2002, 57(1): 115-124.

[10] SHEN Yu-ling, CAI Wen-jian, LI Shao. Normalized decoupling control for high-dimensional MIMO process for application in room temperature control HVAC systems [J]. Control Engineering Practice, 2010, 18(6): 652-664.

[11] RONG Hui-gui, ZHENG Hui, LI Zheng-qiang, XIA Yu-xiang. Tuning of fuzzy PID controller for Smith predictor [J]. Journal of Central South University of Technology, 2010, 17(3): 566-571.

[12] OGUNNAIKE B A, RAY W H. Multivariable controller design for linear systems having multiple time delays [J]. AIChE Journal, 1979, 25(6): 1043-1051.

[13] LIU Tao, ZHANG Wei-dong, GU Dan-ying. Analytical multiloop PI/PID controller design for two-by-two process with time delays [J]. Ind Eng Chem Res, 2005, 44(6): 1832-1841.

[14] WANG Qing-guo, ZOU Biao, ZHANG Yu. Decoupling smith predictor design for multivariable systems with multiple time delays [J]. Chemical Engineering Research and Design Transactions of the Institute of Chemical Engineers: Part A, 2000, 78(4): 565-572.

[15] LI Zhong-shen., WANG Yong-chu. Inverse problems of Butterworth optimal control [J]. Control Theory and Application, 2006, 23(3): 455-457. (in Chinese)

[16] MORARI M, ZAFIRIOU E. Roubust process control [M]. Englewood Cliffs. New York: Prentice Hall, 1989: 310-318.

[17] RICARDO S, SANCHEZ P, YOLANDA B, VICENC P. MIMO Smith predictor: Global and structured robust performance analysis [J]. Journal of Process Control, 2009, 19(1): 163-177.

(Edited by LIU Hua-sen)

Foundation item: Projects(60634020, 61074117) supported by the National Natural Science Foundation of China

Received date: 2010-12-24; Accepted date: 2011-11-24

Corresponding author: HUANG Can, PhD candidate; Tel: +86-731-88830394; E-mail: cancan17@sina.com.cn