
Distribution of electric field for carbon nanotube assembly: Simulation (I)
Soon-Geun KWON1, Soo-Hyun KIM1, Kwang-Ho KIM2, Myung-Chang KANG2, Hyung-Woo LEE2
1. Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology (KAIST),
Daejeon 305-701, Korea;
2. National Core Research Center for Hybrid Materials Solution,
Pusan National University, Busan 609-735, Korea
Received 21 April 2010; accepted 10 September 2010
Abstract: The distribution of electric field for the alignment and attachment of carbon nanotubes (CNTs) was simulated. To be attached at the desired place, the aligned and attracted CNTs should be stayed in the desired area called the stable region or the quasi-stable region for an instant where the change of electric field is minimized. Since the conical electrode has the very narrow sized quasi-stable region, few CNTs can be attached. The rectangular electrodes have a wide stable region, so lots of CNTs can be attached. The results indicate that the round electrode which has a proper sized quasi-stable region is more effective for aligning and attaching a single CNT than the conical or rectangular shaped electrodes.
Key words: carbon nanotubes (CNTs); dielectrophoresis (DEP); round shaped electrode; simulation
1 Introduction
Recently, the hottest issue in nanotechnology is how to expand this technology into the commercialization area. Many researchers discussed the technical possibility for the product commercialization using the nanotechnology, and proved the possibility for that, but there is a far distance to go forward. The perfect solutions for mass production using nanotechnology have not been found yet.
The use of various nano materials in nanoscale science and engineering has been widely researched. Carbon nanotubes (CNTs), in particular, are the most popular subject of research in nanotechnology. Since their discovery in 1991[1], CNTs have been used in many nanoscale applications due to their unique mechanical, electrical and chemical properties. Because of these special characteristics, CNTs are a prime candidate for numerous microscale and nanoscale sensors and devices such as field emitted display (FED), fuel cells, transistors, and chemical or bio sensors[2-6]. Because of the technical limit for CNTs assembly onto a device, however, the product commercialization has been delayed.
Previous research for the CNT assembly was focused on CNTs fabrication by chemical vapor deposition (CVD) method[7-8]. It is proved to be a very effective method since CNTs can be grown at the desired place where the catalyst is located. However, there are some limitations such as non-uniformity of growing conditions and difficult length control of CNTs. A few attempts were reported to attach CNTs on the specific place using the mechanical attachment method[9]. In this case, however, great efforts are needed to assemble CNTs successfully.
In this work, the electric field was used to assembly CNTs on the desired place. Furthermore, the distribution of the electric field was simulated under different shapes of electrodes and the effect of the shape of the electrode was investigated to align and attach CNTs on the desired place.
2 Simulation
2.1 Background theory
Dielectrophoresis which causes the translation motion of neutral matter by the polarization effect arises from a nonuniform electric field. A neural particle such as a CNT polarized in an electric field moves to the region with the highest electric field intensity in a nonuniform electric field.
From this principle, the DEP force was used as a principal driving force to align and attach CNTs at the desired place in this work. The DEP force due to the nonuniform electric field can be expressed by the following equation[10]:
 (1)
(1)
 (2)
(2)
where FDEP is the DEP force; r is the diameter of the particle; l is the longest dimension of the particle; E is R.M.S. of electric field intensity which is generated by alternating current. In Eq.(2), K(ω) is the Clausius- Mossotti equation which is composed of the conductivity and permittivity of a particle and a medium; εp is the dielectric constant of the particle electric field; εm is the dielectric constant of the medium. This force is affected by the applied frequency due to the complex permittivity expression ε*=ε-iσ/ω; σ is the conductivity; and ω is the frequency of the AC electric field which decides the dielectric force as a positive or a negative force.
The DEP force is generated by the dipole moment or the polarizability caused in the ununiform electric field. CNTs are aligned and attracted by the dipole moment or the polarizability in proportion to the degree of ununiformity of electric field. As shown in Eq.(1), a long particle is faster than a short one because a longer particle is affected by higher DEP force than a smaller one. If CNTs are much longer than the impurities, CNTs might be attracted and aligned faster. Fig.1 shows the schematic diagram of CNTs’ alignment and attraction phenomenon by the DEP force.
2.2 Fabrication of electrodes pair
For aligning and attaching CNTs between two electrodes, three different shaped electrodes were made by micro fabrication process, as shown in Fig.2. Through the photolithography process, metal deposition by evaporator, and lift-off processes, aluminum (30 nm thickness) electrodes were patterned on the SiO2 (200 nm) layer.
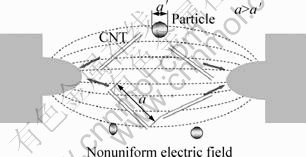
Fig.1 CNT alignment and attraction phenomenon between two electrodes by DEP force

Fig.2 Micro fabrication process for making three different shaped electrodes
Fig.3 shows the optical microscope images of conical, round and rectangular shaped electrodes with 4 μm gap distance made by the micro-electro-mechanical system (MEMS) process.
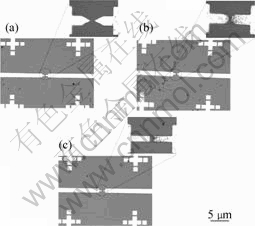
Fig.3 Fabricated conical (a), round (b), and rectangular (c) shaped electrodes by MEMS process
2.3 Simulation of electric field
The multiphysics modeling and simulation program, FEMLAB?, was used to analyze the distribution of electric field. The Maxwell equation was applied as a govern equation for the electric field in Eq.(3):
 (3)
(3)
where  is the electrical potential; and E is the electric field vector.
is the electrical potential; and E is the electric field vector.
Fig.4 shows the boundary conditions for the simulation of the distribution of the electric field. The Dirichlet boundary conditions were applied to ①, ②,③,⑦,⑧,⑨ and the Neumann boundary conditions were applied to ④,⑤,⑥,⑩,?,? where were insulation parts.
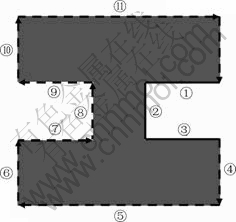
Fig.4 Boundary conditions for simulation of distribution of electric field (①, ②, ③: Ground voltage (V=0); ⑦, ⑧, ⑨: Given voltage (V=10 V); ④, ⑤, ⑥, ⑩, ?, ?: Insulation condition)
The gap distance between two electrodes was set by 4 μm, 10 V was applied at different electrodes such as conical, round and rectangular shaped electrodes.
3 Results and discussion
For analyzing the distribution of the electric field in different shaped electrodes, the conical, round and rectangular shaped electrodes were designed.
CNTs are expected to be aligned and attracted to the area of the highest DEP force. In order to be attached between the electrodes, these aligned and attracted CNTs should be stayed at the desired place called the stable region or the quasi-stable region where the change of the electric field is minimized.
Even though CNTs are aligned and attracted to the area by the high DEP force, there is no temporal and spatial room for CNTs to stay and attach at the place where the DEP force is changed rapidly. As shown in Eq.(1), the DEP force is proportional to the square of the gradient of the electric field. If the gradient of electric field is nearly zero, the DEP force will be minimized. Thus, the stable or quasi-stable area will be formed.
Fig.5 shows the simulation results of the distribution of electric field in the conical shaped electrodes. In Fig.5(a), the high intensity of the electric field is generated at the end of electrodes. As shown in Fig.5(c), however, the area called the quasi-stable region where the gradient of the electric field is zero is very narrow. From this result, it can be expected that few of CNTs can be stayed at the apex of electrodes and attached.
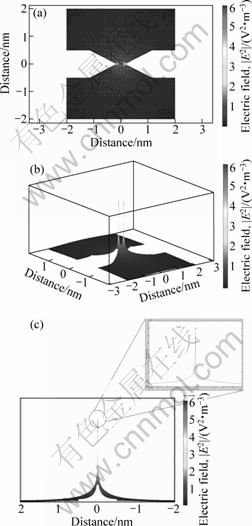
Fig.5 2D- (a), 3D- (b) and lateral-distribution (c) of electric field in conical shaped electrodes
On the other hand, the round shaped electrodes have a wider quasi-stable region in comparison with the conical shaped electrodes. In Fig.6, a wider quasi-stable region at the middle of two electrodes can be seen. The round shaped electrodes are expected for more CNTs to be attached than the conical shaped electrodes.
The rectangular shaped electrodes show different distributions of the electric field. As shown in Fig.7, the rectangular electrodes have stable and quasi-stable regions. A quasi-stable region is located at the edge of the electrodes and stable region is located in the middle of the electrodes. Since the quasi-stable region in the rectangular electrodes is very narrow, however, lots of CNTs are expected to be gathered at the middle of electrode where is wide stable region.
From the simulated distribution of electric field according to the three different shaped electrodes, CNTs are expected to be stayed and attached between the round or rectangular shaped electrodes. To align and attach a single CNT on the electrodes, the round shaped electrodes are expected to be more effective than conical or rectangular shaped electrodes. By selecting the shape of electrodes, the number of CNTs attached at the desired place can be controlled.
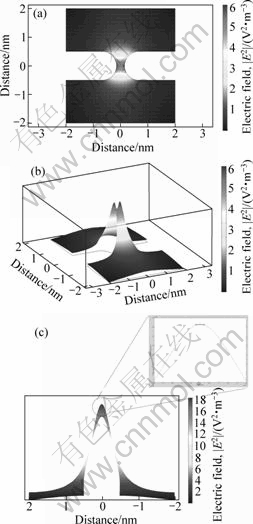
Fig.6 2D- (a), 3D- (b) and lateral-distribution (c) of electric field in round shaped electrodes
4 Conclusions
1) The distribution of electric field in different shaped electrodes (the conical, the round and the rectangular shaped electrodes) was investigated.
2) The round shaped electrode is much more effective for aligning and attaching a single CNT than the conical or rectangular shaped electrodes because the round shaped electrode has the proper sized quasi-stable region where the change of the electric field is minimized. On the other hand, the conical shaped electrodes have a very narrow quasi-stable region and the rectangular shaped electrodes have a wide stable region.
3) In the future work, we will try to align and attach CNTs on different shaped electrodes, and find optimal conditions for attaching a single CNT between two electrodes.
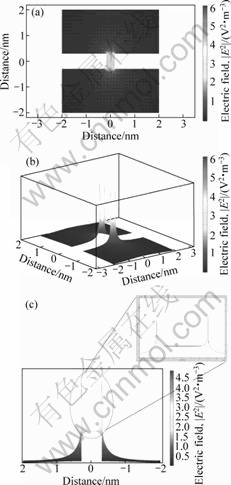
Fig.7 2D- (a), 3D- (b) and lateral-distribution (c) of electric field in rectangular shaped electrodes
References
[1] IIJIMA S. Helical microtubules of graphitic carbon [J]. Nature, 1991, 354: 56-58.
[2] RUECKES T, KIM K, JOSELEVICH E, TSENG G Y, CHEUNG C, LIEBER C M. Carbon nanotube-based nonvolatile random access memory for molecular computing [J]. Science, 2000, 289: 94-97.
[3] BIERCUK M J, MASON M, MARCUS C M. Local gating of carbon nanotubes [J]. Nano Letters, 2004, 4(1): 1-4.
[4] BACHTOLD A, HADLEY P, NAKANISHI T, DEKKER C. Logic circuits with carbon nanotube transistors [J]. Science, 2001, 294: 1317-1320.
[5] KONG J, FRANKLIN N R, ZHOU C, CHAPLINE M G, PENG S, CHO K, DAI H. Nanotube molecular wired as chemical sensors [J]. Science, 2000, 287: 622-625.
[6] DAI H. Nanotube growth and characterization [J]. Topics Applied Physics, 2001, 80: 29-53.
[7] DAI H, HAFNER J H, RINZLER A G, COLBERT D T, SMALLEY R E. Nanotubes as nanoprobesin scanning probe microscopy [J]. Nature, 1996, 384: 147-150.
[8] MCEUEN P L. Single-walled carbon nanotube electronics [J]. IEEE Transaction on Nanotechnology, 2001, 1(1): 78-85.
[9] HALL A, MATTHEWS W G, SUPERFINE R, FALVO M R, WASHBURN S. Simple and efficient method for carbon nanotube attachment to scanning probes and other substrates [J]. Applied Physics Letters, 2003, 82(15): 2506-2508.
[10] POHL H A. Dielectrophoresis: The behavior of neutral matter in nonuniform electric field [D]. London: Cambridge University, 1978: 171-210.
(Edited by CHEN Wei-ping)
Foundation item: Project supported by the Pusan National University Research Grant; Project(2010-0008-276) supported by NCRC (National Core Research Center) through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology
Corresponding author: Hyung-Woo LEE; Tel: +82-51-510-3160; E-mail: LHW2010@pusan.ac.kr; Myung-Chang KANG; Tel: +82-51-510-2361; E-mail: kangmc@pusan.ac.kr