具有不确定变摩擦因数的磁悬浮系统
T-S模糊观测器的设计
周丽杰1, 2,郭树理1, 2,高哲1, 2
(1. 北京理工大学 自动化学院,北京,100081;
2. 北京理工大学 复杂系统智能控制与决策教育重点实验室,北京,100081)
摘要:针对含不确定变摩擦因数的非线性磁悬浮系统设计一种模糊观测器。首先将非线性磁悬浮系统进行T-S模糊处理,利用添加辅助变量的方法放宽了Lyapunov方法设计观测器的局限性,具有较小的保守性。最后仿真结果验证了该方法的有效性。仿真结果表明:设计的观测器对磁悬浮系统在不确定摩擦因数情形下能够有效地观测位置输出变化信息。该方法对于这类含不确定参数的非线性系统具有参考价值。
关键词:磁悬浮;变摩擦因数;T-S模糊系统;观测器
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2011)S1-0114-05
T-S fuzzy observer for nonlinear magnetic levitation system with uncertain variable friction coefficient
ZHOU Li-jie1, 2, GUO Shu-li1, 2, GAO Zhe1, 2
(1. School of Automation, Beijing Institute of Technology, Beijing 100081, China;
2. Key Laboratory of Complex system Intelligent Control and Decision, Ministry of Education,
Beijing Institute of Technology, Beijing 100081, China)
Abstract: An adaptive fuzzy observer for nonlinear magnetic levitation system with uncertain friction coefficient is proposed. First, a T-S fuzzy model of the nonlinear magnetic levitation system is proposed. An observer is given by LMI method and the Lyapunov method. Through adding an auxiliary variable, it relaxes the constraint of the design of observer. The proposed approach is a more relaxed condition than others. Simulation results show the effectiveness of this approach. The results show that the position of magnetic levitation system is estimated effectively with unknown friction coefficient. There is some reference value for a kind of nonlinear systems with unknown parameter.
Key words: magnetic levitation system; uncertain friction coefficient; T-S fuzzy system; observer
磁悬浮技术由于具有低摩擦、低噪声、速度快、无污染等优点,现在已经广泛地应用于工业、教学等场合[1]。但是,在准确控制磁悬浮系统的位置和速度等面,其本身存在的微小摩擦是不可忽略的,而且摩擦因数随着时间和环境的变化会发生改变,随时导致模型的改变,以至于对磁悬浮系统的实际位置测量方面不精确。在此,本文设计了一种模糊观测器,使得磁悬浮系统在摩擦因数未知的情况下有效地观测位置输出变化信息。磁悬浮系统是典型的非线性系统,本文将含有未知参数的磁悬浮非线性系统转化为T-S模糊系统[2]。Nguang等[3]提出了一种基于线性矩阵不等式的输出反馈控制器;Tong等[4]提出了具有参数不确定性的鲁棒观测器;Wang等[5]设计了并联分散补偿控制器,该方法主要是靠驱动控制规则来补偿模糊系统的每个规则,设计简单方便。Park等[6]针对系统矩阵参数未知的T-S模糊系统设计了一类基于Lyapunov方法的观测器,但是如果系统状态不完全可测,此观测器的自适应律中就不可以直接使用状态误差。Xu 等[7-8]利用添加辅助变量的方法设计一类时变系统等的自适应观测器。本文中磁悬浮系统的变摩擦因数可以看成是未知参数,这样将这类含有未知参数的磁悬浮非线性系统转化为T-S模糊系统,基于Lyapunov方法通过添加辅助变量放宽了观测器的约束条件,实现对磁悬浮系统的位置输出的有效观测。
1 磁悬浮系统的T-S模糊模型的建立
1.1 磁悬浮系统
本文中的磁悬浮系统M730[9]是美国ECP公司生产(见图1),包括磁盘、玻璃柱、传感器、磁力线圈。其中传感器用于测量磁盘的位置,磁力线圈将系统的直流电流输入转化为磁场,由磁场对磁盘的作用力、磁盘与玻璃棒之间的摩擦力及磁盘自身的重力,得出动力学方程为:
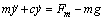 (1)
(1)
其中:m为磁盘的质量;y为磁盘的位置;c为摩擦因数;g为重力加速度;Fm为作用于磁盘上的磁力。磁力可以写成如下形式
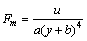 (2)
(2)
其中:a和b为正常数;u为输入(电流)。
摩擦因数可以写成如下形式:
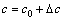 (3)
(3)
其中:c0为标准摩擦因数;?c为时变不确定参数。

图1 M730磁悬浮系统
Fig.1 Magnetic levitation system
从式(1)~(3)可以得到磁盘位置和电流量之间的非线性方程:
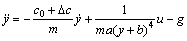 (4)
(4)
式中:a=1.04×10-4 A/(N?cm4),b=6.2 cm(经传感器参数辨识得到),g=9.81 m/s2,m=0.12 kg,c0=0.15 N?s/m。
1.2 磁悬浮系统的T-S模糊模型的建立
一般地,T-S模糊模型的特点是前件变量是用模糊语言描述的,而其后件变量是一个精确的数学表达式,而传统的Madani模型后件变量仍是模糊语言描述的。通常T-S模糊系统的后件变量是局部子系统的线性模型[10-15]。
考虑如下的磁悬浮系统[16]:
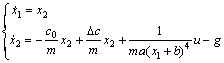 (5)
(5)
其中:x1满足s≤x1≤S;n≤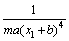 ≤N;x2满足w≤x2≤W;未知参数?c=θ。则依据T-S模糊规则, 上述系统的T-S模糊模型如下:
≤N;x2满足w≤x2≤W;未知参数?c=θ。则依据T-S模糊规则, 上述系统的T-S模糊模型如下:
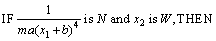
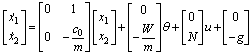
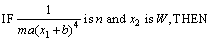
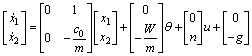
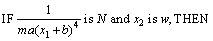
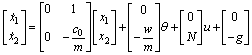
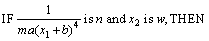
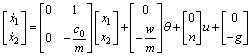
其中分别对应的隶属度函数如下:
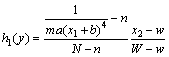
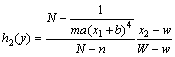
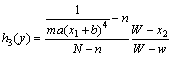
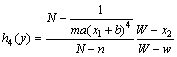
2 含不确定摩擦因数的磁悬浮系统的T-S模糊观测器设计
据系统(5),设计如下的模糊观测器:
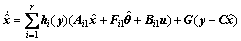 (6)
(6)
定义误差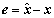 ,
,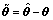 并假设
并假设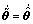 ,
,
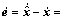
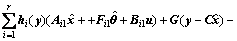
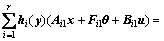
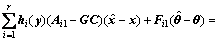
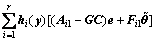 (7)
(7)
定义如下Lyapunov函数:
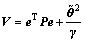 (8)
(8)
其中:P是一个正定矩阵,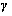 >0,则有:
>0,则有:
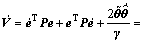
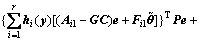
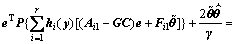
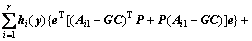
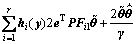 (9)
(9)
若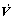 <0,则每个子系统必须满足:
<0,则每个子系统必须满足:
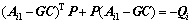 (10)
(10)
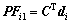 (11)
(11)
其中:Qi是一个正定矩阵,即要求每个子的传递函数都是正实函数。满足上式的自适应律为:
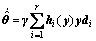 (12)
(12)
那么,有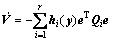 <0。
<0。
引理1[12] 如果系统(5)每个子系统必须满足(10)和(11),且设计自适应律为(12)时,系统(5)是渐近稳定的。
但引理1的难点在于要求每个子系统未知参数矩阵Fi1都满足式(11),需要简化。
下面进一步采用了添加辅助变量的方法,对引理1得到的判据进一步放宽。
对于系统(5),如果将不确定参数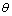 看成系统的另一个输入信号,将系统状态x可以分解为
看成系统的另一个输入信号,将系统状态x可以分解为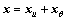 。其中xu是与控制信号u有关的状态,
。其中xu是与控制信号u有关的状态,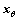 是与参数
是与参数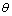 有关的状态,那么系统(5)描述的状态方程可以分解为:
有关的状态,那么系统(5)描述的状态方程可以分解为:
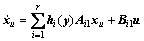 (13)
(13)
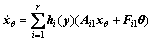 (14)
(14)
针对式(13)和(14)设计的观测器如下:
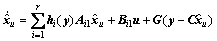 (15)
(15)
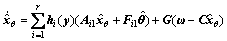 (16)
(16)
其中:G是需要设计的向量;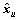 ,
,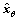 和
和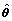 分别是
分别是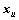 ,
,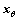 和
和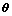 的估计值;
的估计值;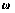 是用来补偿观测误差的辅助向量。
是用来补偿观测误差的辅助向量。
假设存在一个时变的向量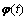 使得
使得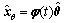 ,则式(16)变为:
,则式(16)变为:
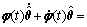
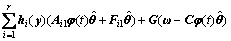 (17)
(17)
令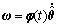 ,则
,则
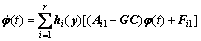 (18)
(18)
合并式(13)和式(14),可以得到系统(5)的观测器 如下:
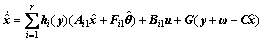 (19)
(19)
定理1 假设u是持续激励信号,如果存在正的常数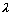 和向量G满足
和向量G满足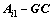 <0,要使观测器误差
<0,要使观测器误差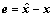 和参数估计误差
和参数估计误差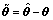 渐近趋向于0,那么,观测器设计如下:
渐近趋向于0,那么,观测器设计如下:
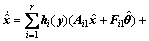
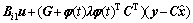 (20)
(20)
其中自适应律为:
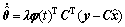 (21)
(21)
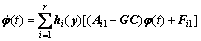 (22)
(22)
3 仿真
依据本文给出的模糊模型(5)和定理1的观测器进行系统仿真,其中: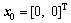 ,n=7.4,N=54.23,w=0,W=0.1。设G=[1, 1]T,λ=50仿真结果如图2~5所示。其中图2所示为位置及其观测值变化曲线,图3所示为位置变化误差曲线。从图2和图3可以看出观测器可以有效地观测位置,位置误差大约在0.06 s接近于0。图4所示为摩擦因数及其观测值变化曲线,图5所示为摩擦因数的估计误差曲线。从图4和图5可以看出摩擦因数是时变的,观测器基本可以随时有效地获得未知摩擦因数,且观测误差在0.07 s时接近于0。
,n=7.4,N=54.23,w=0,W=0.1。设G=[1, 1]T,λ=50仿真结果如图2~5所示。其中图2所示为位置及其观测值变化曲线,图3所示为位置变化误差曲线。从图2和图3可以看出观测器可以有效地观测位置,位置误差大约在0.06 s接近于0。图4所示为摩擦因数及其观测值变化曲线,图5所示为摩擦因数的估计误差曲线。从图4和图5可以看出摩擦因数是时变的,观测器基本可以随时有效地获得未知摩擦因数,且观测误差在0.07 s时接近于0。
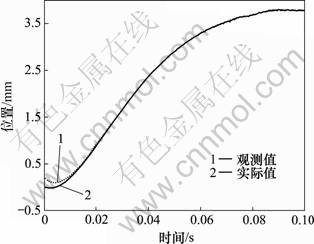
图2 位置y及其观测值
Fig.2 Distance y and its estimation
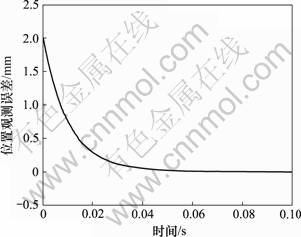
图3 位置观测误差
Fig.3 Estimation error of distance
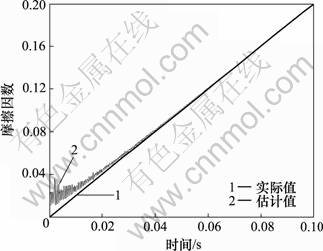
图4 摩擦因数c及其观测值
Fig.4 Friction coefficient c and its estimation
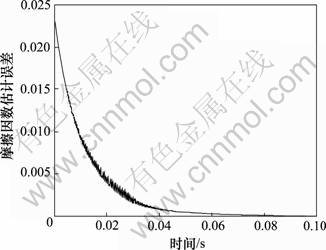
图5 摩擦因数估计误差
Fig.5 Estimation error of friction coefficient
4 结论
本文对具有不确定摩擦因数的非线性磁悬浮系统设计模糊观测器。首先通过T-S模糊处理方法将磁悬浮系统转化为T-S模糊模型,通过添加辅助变量的方法,放宽了一般基于Lyapunov方法设计的观测器。通过设计向量G和参数λ可以控制观测误差和参数估计误差的收敛速度。仿真结果显示:当摩擦因数?c发生变化时,观测器仍能快速有效地得到位置输出信息。本文的优点在于解决了通常磁悬浮的控制中普遍采用固定的摩擦因数或直接忽略摩擦项的不足。该方法对于这类含不确定参数的非线性系统具有参考价值。
参考文献:
[1] 蒋金周. 磁悬浮技术及其应用与发展分析机电一体化[J]. 机电一体化, 2004(1): 25-27.
JIANG Jin-zhou. The technique of magnetic float and its application development analysis[J]. Electromechanical Integration, 2004(1): 25-27.
[2] Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on Systems, Man and Cybernrtics, 1985, 15(1): 116-132.
[3] Nguang S K, Shi P. Fuzzy output feedback control design for nonlinear systems: An LMI approach[J]. IEEE Transactions on Fuzzy Systems, 2003, 11(3): 331-340.
[4] TONG Shao-cheng, LI Han-Hiong. Observer-based robust fuzzy control of nonlinear systems with parametric uncertainties[J]. Fuzzy Sets and Systems, 2002, 131(2): 165-184.
[5] Wang H O, Tanaka K, Griffin Michael F. An approach to fuzzy control of nonlinear systems: Stability and design issues[J]. IEEE Transactions on Fuzzy Systems, 1996, 4(1): 14-23.
[6] Park C W, Cho Y W. T-S model based indirect adaptive fuzzy control using online parameter estimation[J]. IEEE Transactions on Systems, Man and Cybernetics. Part B: Cybernetics, 2004, 34(6): 2293-2302.
[7] XU Ai-ping, ZHANG Qing-hua. Nonlinear system fault diagnosis based on adaptive estimation[J]. Automatica, 2004, 40(7): 1181-1193.
[8] ZHANG Qing-hua. Adaptive observer for multiple-input- multiple-output (MIMO) linear time-varying systems[J]. IEEE Transactions on Automatic Control, 2004, 47(3): 525-529.
[9] Anderson B D, Bitmead R R, Johnson C R, et al. Stability of adaptive system: Passivity and averaging analysis[M]. Cambridge, American: MIT Press, 1996: 6-38.
[10] Tanaka K, Wang H O. Fuzzy control system design and analysis: A linear matrix inequality approach[M]. New York: Wiley, 2001.
[11] Guerra T M, Vermeiren L. Control law for takagi-sugeno fuzzy models[J]. Fuzzy Sets and Systems, 2001, 120: 95-108.
[12] Wang H O, Tanaka Kazuo, Griffin Michael F. Parallel distributed compensation of nonlinear systems by takagi-sugeno fuzzy models[J]. Proc Fuzzy IEEE/IFES, 1995, 95: 531-538.
[13] Yoneyama J. H∞ output feedback control for fuzzy systems with immeasurable premise variables: Discrete-time case[J]. Applied Soft Computing, 2008, 8(2): 949-958.
[14] Liu X D, Zhang Q L. Approaches to quadratic stability conditions and H∞ control designs for takagi-sugeno fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2003, 11(3): 830-839.
[15] Silva E B. Modeling and controlling a magnetic levitation system[D]. Salvador Bahia: Dept Elect Eng. UFBA Univ, 2009.
[16] Ecp Experimental Systems. Manual for Model 730 Magnetic Levitation[M]. 1999.
(编辑 陈灿华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:教育部留学归国人员启动基金资助项目(20100632001);北京市新星计划项目(2008B54);北京理工大学科研基地科技支撑计划资助项目(2011CX02010)
通信作者:周丽杰(1987-),女,黑龙江哈尔滨人,硕士研究生,从事非线性模糊控制研究;电话:13810281154;E-mail: zhoulijie0105@yahoo.cn