DOI：10.19476/j.ysxb.1004.0609.2019.07.19

全覆式离子型稀土矿山临界注液范围的计算

洪本根¹，罗嗣海²，胡世丽²，王观石²

(1. 江西理工大学 资源与环境工程学院，赣州 341000；

2. 江西理工大学 建筑与测绘工程学院，赣州 341000)

摘  要：掌握全覆式离子型稀土矿山临界注液范围的计算方法对于合理确定矿山注液范围具有重要意义。通过注液边界将潜在滑坡体分为两部分：注液区潜在滑坡体提供下滑力，未注液区潜在滑坡体提供抗滑力。基于黏性土土压力的计算方法和简化Bishop法，建立稳渗状态下矿山临界注液范围的理论模型，并基于数值计算结果和现场位移监测结果验证理论模型的有效性。结果表明：首先，对于坡度为25°、30°或35°的简单边坡，临界注液范围理论模型计算值与数值模型计算值的相对误差绝对值在20%以内，相对误差绝对值较小，初步说明临界注液范围理论计算模型的有效性；其次，对于某一现场边坡，理论模型计算的边坡安全系数与其边坡位移变化规律吻合，再次说明了临界注液范围理论计算模型的有效性。

关键词：离子型稀土矿山；下滑力；抗滑力；边坡安全系数；临界注液范围

文章编号：1004-0609(2019)-07-1509-10　　     中图分类号：TD865　　     文献标志码：A

对于离子型稀土矿，目前采用的是原地浸矿工艺^[1]。在推广该工艺的20多年间，也暴露出该工艺的不足，如注液范围的确定主要依赖于经验，当注液范围确定不合理时，则引发滑坡等地质灾害^[2]，造成滑坡区域资源的浪费。因此，确定原地浸矿时离子型稀土矿山的临界注液范围具有重要的工程意义。

传统的边坡稳定性评价方法主要有极限平衡法^[3-4]和数值分析法^[5-6]，但这两种方法运用于离子型稀土矿山的临界注液范围的确定均存在一定的缺陷。对于极限平衡法，其需事先假定不同的滑移面，而后把土体进行条分，并进一步假定条块之间的作用力分布情况，以此来计算某假定滑移面条件下的边坡安全系数，从而确定最危险滑移面，故其计算结果受所选土条宽度的影响较大^[7]，且计算过程繁琐^[8]。对于数值分析法，由于离子型稀土矿山收液工程具体布置方式难以准确确定，且深层原位矿体的物理力学参数获取难度较大，特别是原位矿体的土水特征曲线和渗透系数，这对数值分析法运用于矿山临界注液范围的计算造成一定的限制^[9]。

为提供一种简便的全覆式离子型稀土矿山临界注液范围计算模型，本文在充分考虑稀土矿山原地浸矿基本特点的基础上，通过注液边界将潜在滑坡体分为两部分，注液区潜在滑坡体提供下滑力，未注液区潜在滑坡体提供抗滑力，结合黏性土土压力和简化Bishop法的计算原理，建立了临界注液范围计算模型，为现场矿山确定注液范围提供一定的理论指导。

1   临界注液范围的计算模型

对于原地浸矿工艺，其是在矿山一定范围内按菱形状布置注液孔，而后由注液孔直接向矿体内部注入浸矿剂溶液，使浸矿剂溶液与矿体中的稀土离子发生交换反应，形成浸出液后由收液工程流出^[10]，其简化模型如图1所示。因此，就全覆式离子型稀土矿山而言，在浸矿和收液工程作用下，注液影响范围内的矿体含水率会发生改变且矿体强度会发生弱化，注液影响范围外的矿体不受影响，故该类型稀土矿山的滑坡以推移式为主，潜在滑坡体部分位于注液区，部分位于非注液区^[11]，由此采用如下思路建立临界注液范围的计算模型。

1.1  下滑力的计算模型

以注液边界为分界线，将潜在滑坡体分为上下2个部分，则位于注液区的上部滑体提供下滑力，位于未注液区的下部滑体提供抗滑力。若未注液区潜在滑坡体简化成“挡墙”面，可建立注液区域潜在滑坡体的计算模型，如图2所示。根据图2，将注液区域潜在滑坡体简化成三角形ABC，则AB面为注液边界面，即为“挡墙”面，AC面为矿层上表面，BC面为滑移面，AC面与水平面成β₁角。由于滑体ABC处于矿层，则令矿体的黏聚力和内摩擦角分别为c₁和φ₁，矿体的容重为γ₁，滑体ABC与挡墙面的外摩擦角为δ^[12]。

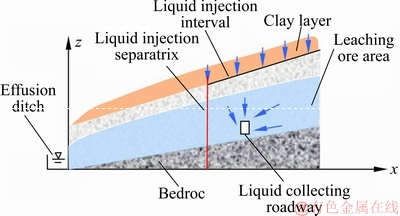
图1  原地浸矿的简化模型

Fig. 1  Simplified model of in-situ leaching

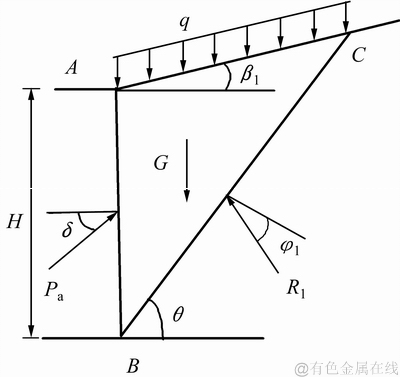
图2  下滑力的计算模型

Fig. 2  Calculation model of downslide strength

根据原地浸矿的特点，浸矿液不对表土产生影响，为简化计算，将覆盖于矿层上表面的表土看成均布荷载q，其均匀作用于AC面上。在矿体具有黏性的情况下，注液区域矿体的黏聚力c₁也可以采用等效法则来处理，即将其看作是一种内结构压力，其均匀的作用在滑体ABC的四周。故ABC滑体所受的作用力：AB面上作用有法向均布荷载和土压力P_a，土压力P_a的大小即为下滑力；AC面上作用有竖直向下的均布荷载q，内结构压力的竖向分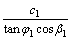力和均布切力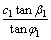，均布切力作用方向沿AC面向上；BC面上作用有下部矿体对滑体的支撑力R₁，R₁的方向指向滑体ABC；滑体ABC的形心处作用有滑体的重力G。

根据计算模型中的几何关系，滑裂体的重量G为：

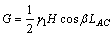                          (1)

式中：L_AC为滑裂体ABC的AC边长度；γ₁为注液区域矿体的重度。

作用在AB面上的法向力F为

                       (2)

式中：L_AB为滑裂体ABC的AB边长度；c₁为注液区域矿体的黏聚力；φ₁为注液区域矿体的内摩擦角。

作用在AC面上的竖直方向的作用力合力Q₁为

                (3)

作用在AC面上的切力J为

                          (4)

在P_a、R₁、Q₁、F、J、G等力的作用下，滑裂体ABC处于平衡状态，由此推导出下滑力P_a的计算公式如式(5)所示：

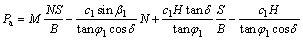  (5)

关系式(5)中M、B、N、S分别采用关系式(6)~(9)进行计算：

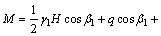
     (6)

 (7)

           (8)

          (9)

1.2  抗滑力的计算模型

在边坡稳定性分析的工程问题中，目前学者常常采用简化的Bishop法和非圆弧滑面来进行计算^[13]。由此，设滑移面为非圆弧面，根据简化Bishop法^[14]，给出抗滑力的计算模型，如图3所示。

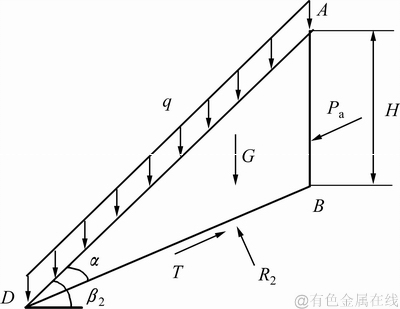
图3  抗滑力的计算模型

Fig. 3  Calculation model of anti-sliding force

故ABD滑体所受的作用力有：AB面上作用有下滑力P_a；AD面上作用有竖直向下的均布荷载q；BD面上作用反力R₂以及抗剪力T；滑体ABC的形心处作用有滑体的重力G。

同理，作用在抗滑体上竖直方向的作用力合力Q₂为

                   (10)

式中：q为上覆表土转化的荷载；L_AD为抗滑段的坡面长度，γ₂为未注液区域矿体的重度，β₂为未注液区域边坡的坡角。

在P_a、R₂、Q₁、T等力的作用下，滑体ABD处于平衡状态，在不考虑下滑力P_a的影响，则可求得滑体ABD所能提供的实际抗滑力T_s，计算公式如下：

  (11)

式中：c₂和φ₂为未注液区域矿体的黏聚力和内摩擦角，L_BD为抗滑段滑移面的长度；α为潜在滑移面和坡面的夹角。

由图3中计算模型的几何关系可得

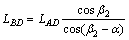                       (12)

将式(13)代入式(12)可得实际抗滑力的计算公式：

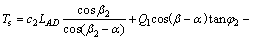
    (13)

稳渗状态下，“挡墙”面处的下滑力等于抗滑力，则滑坡体处于临界安全状态，此时的注液范围即为临界注液范围。

2  临界注液范围计算模型分析

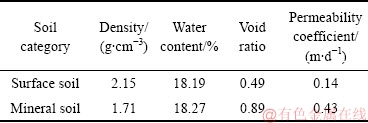
在屏南选定某全覆式稀土矿山一陡坡区域，确定该区域表土厚度。通过取原状样测试表土和矿土的初始密度和初始含水率，通过单环法现场测试表土和矿土的渗透系数，具体参数如表1所列。

表1  离子型稀土土体物理性质指标

Table 1  Physical property indexes of ion-type rare earth soil

2.1  矿体抗剪强度的现场测试

由于浸矿液对矿体的抗剪强度参数有弱化作用，故在3 m×3 m的尾矿区域内选取15个干密度与所测干密度相同的测点，现场测试尾矿的抗剪强度参数。

现场测试时，通过人为注水的方式改变各个测点的体积含水率，待各个测点体积含水率基本稳定后，采用APAGEO原位钻孔剪切仪现场测试矿体的抗剪强度参数，测点深度为4.0 m左右，测试图如图3所示，测试步骤主要包括：1) 在测试地层中钻孔，并通过取样器清孔使孔壁光滑；2) 将探头放入孔中，加压使探头膨胀使得侧刃嵌入周围土体中；3) 利用千斤顶对探头施加垂直向上的提拉力，使得嵌入土体的侧刃对周围土体进行剪切，通过测力装置测定剪切时的剪切应力。

图4  矿体抗剪强度现场测试图

Fig. 4  Field test chart of shear strength of ore body

根据现场原位剪切试验结果，并取样室内测试对应测点的体积含水率，可得浸矿后矿体的黏聚力和内摩擦角与体积含水率的关系，如图5和6所示。

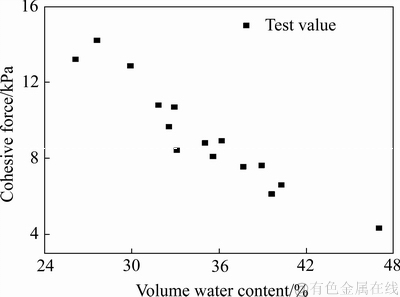
图5  黏聚力与体积含水率的关系

Fig. 5  Relationship between cohesive force and volume water content

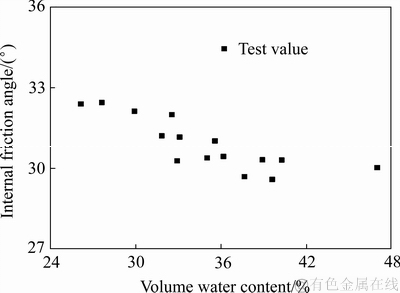
图6  内摩擦角与体积含水率的关系

Fig. 6  Relationship between internal friction angle and volume water content

由图5和6可知，随着体积含水率的不断减小，矿体的黏聚力大幅增加，内摩擦角略有增加，上述现象产生的原因：随着体积含水率的不断减小，基质吸力逐渐增大，矿体进入非饱和状态，孔隙水逐渐减少，孔隙气慢慢增多，毛细作用机制增强，水－气接触面的收缩膜产生的表面张力逐渐增大，造成矿体黏聚力的增大；同时，随着进入矿体孔隙气的增多，孔隙水逐渐减少，土颗粒间水分的润滑作用减弱，矿体内摩擦角略有增大^[15-16]。

鉴于此次试验结果，判定内摩擦角不受矿体含水率的影响，取矿体饱和时所对应的内摩擦角，即内摩擦角为30.03°。同时，为进一步分析矿体黏聚力随其体积含水率的变化规律，对其进行曲线拟合，如图7所示。由图7可知，当矿体体积含水率由天然含水率增大至饱和含水率时，其黏聚力的对数与体积含水率呈现良好的线性关系，用式(14)描述。

                                (14)

式中：c为黏聚力；θ为体积含水率；a和b为拟合参数，a=-2.40，b=1.78，相关系数为0.95。

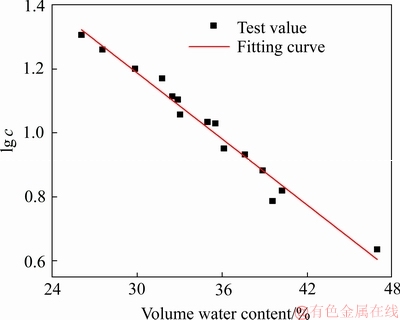
图7  黏聚力的对数与体积含水率的关系

Fig. 7  Relationship between logarithm of cohesive force and volume of water content

2.2  不同体积含水率下矿体浸取率的测试

矿体天然状态下的密度为1.71 g/cm³，体积含水率为0.28，稀土离子品位为0.065%，据此制作矿样，矿样直径10 cm，高度35 cm；自柱浸桶底部开始自下而上放置透水石、滤纸、粗砂、矿样、滤纸和粗砂，装置如图8所示。试验通过调节蠕动泵流量来控制矿样体积含水率，矿样体积含水率的变化范围为0.314~0.384；试验开始时，先用去离子水以恒定流速在矿土中形成稳定流场(流进、流出水量或流速相等)，再将去离子水置换成浓度为20 g/L的硫酸铵溶液，开始恒定流速下的非饱和浸矿试验；从注硫酸铵溶液开始，每隔100 g收集一次浸取液，并化验浸取液中的稀土离子；待浸取液中稀土离子浓度下降到0.01 g/L以下时，试验结束。

图8  非饱和柱浸试验图

Fig. 8  Column leaching tests chart of unsaturated soil

将室内试验结果进行整理，可得矿体的浸取率和浸矿周期与其体积含水率的关系，如图9和10所示。由图9可知，随着矿体体积含水率的增大，矿体的浸取率逐步增大，两者呈负指数函数关系，用式(15)描述。由图10可知，随着矿体体积含水率的增大，矿体的浸矿周期逐步减小，并趋于稳定。

                              (15)

式中：h为稀土离子的浸取率；h_max为稀土离子的最大浸取率，取值90.50%；θ为矿体的体积含水率；k、d为拟合参数，其中k=0.49，d=28.64。

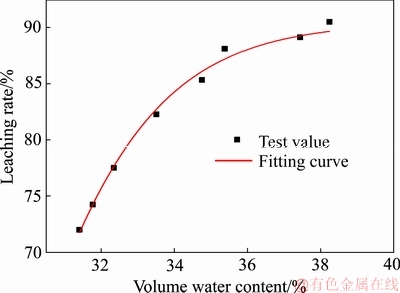
图9  矿体浸取率与体积含水率的关系

Fig. 9  Relationship between ore body leaching rate and volume water content

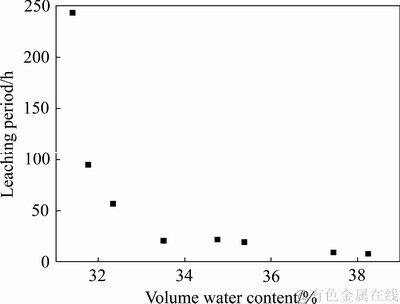
图10  浸矿周期与体积含水率的关系

Fig. 10  Relationship between leaching period and volume water content

2.3  临界注液范围计算模型的验证

2.3.1  基于数值计算的模型有效性分析

将矿山边坡简化为平面二维边坡，则注液范围可定义为二维边坡中注液坡面长度。由于本文所建模型是用于预测稀土矿山的注液范围，则需假定注液区域内矿体含水率大小。根据室内柱浸试验结果可知，当矿体含水率达到0.38时，矿体资源浸取率可达90%，接近于最大浸取率，此时矿样上部已有0.5 cm左右的积水，由此表明矿样饱和度难以进一步上升，且此时的浸矿周期为一稳定值。因此，综合考虑矿体的浸取率和浸矿周期后，在进行模型计算时，可假定注液区域矿体的含水率为0.38。

为验证模型的有效性，现计算水平长度为30 m，坡度分别25°、30°和35° 3种边坡的临界注液范围，现以坡度为25°的边坡为算例进行计算说明。

取初始注液范围为15.28 m，对于注液区域，坡体表面与水平面的夹角β₁=25°；稳渗状态下矿层体积含水率为0.38，则矿层重度γ₁=18.20 kN/m³；根据式(14)计算可得矿层黏聚力c₁=7.27 kPa；内摩擦角φ₁=30.03°；对于填土与墙面的摩擦角δ，不仅要考虑墙面的倾斜情况，而且要考虑墙面的粗糙程度，对于试验矿区墙面粗糙、排水不良的情况，宜取δ=0.33φ₁≈10°^[12]；试验矿区表土平均厚度在2 m左右，转化为均布压力q=43.00 kPa；对于见矿深度H，以矿层上表面为起始点，沿深度方向以0.1 m为步长进行取值；将各参数值代入式(5)可计算不同见矿深度下的下滑力P_a。

对于未注液区域，因滑坡体一般先于坡脚处发生破坏^[17]，取L_BD=19.12 m；坡脚β₂=25°；同理，对于见矿深度H，以矿层上表面为起始点，沿深度方向以0.1 m为步长进行取值；根据几何关系可求得不同见矿深度下的α值；表土平均厚度在2 m左右，转化为均布压力q=43.00 kPa；根据式(14)可求得抗滑区滑面上矿层黏聚力c₂=12.30 kPa、内摩擦角φ₂=30.03°；将各参数代入式(13)计算可得不同见矿深度处抗滑力T_s。

边坡安全系数是指假定滑裂面上抗滑力与下滑力的比值，根据求取的不同见矿深度的抗滑力与下滑力，可求得边坡安全系数随见矿深度的变化规律，如图11所示。为更好地反应边坡安全系数随见矿深度的变化规律，图11中仅给出了见矿深度为3.5~7 m段的数据。由图11可知，随着见矿深度的增加，边坡安全系数先减小后增大，当见矿深度为6.1 m时，边坡安全系数达到最小值1.812，但大于1，表明在该注液范围下，边坡是稳定的。

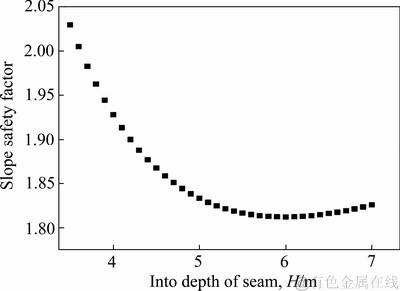
图11  边坡安全系数随见矿深度的变化规律

Fig.11  Change law of slope safety factor with depth of entering seam

故在现有注液范围的基础上沿坡面方向以1m为步长逐步增大注液范围，重新根据式(5)和式(13)计算边坡安全系数随见矿深度的变化规律，确定各注液范围下的最小边坡安全系数，从而确定最小边坡安全系数随注液范围的变化规律，如图12所示。由图12可知，随着注液范围的增大，最小边坡安全系数基本呈线性减小，当注液范围达到26.28 m时，最小边坡安全系数约为1，则该注液范围即为临界注液范围。

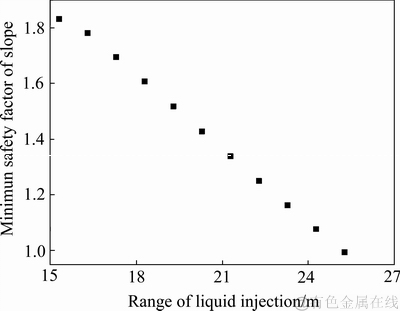
图12  最小边坡安全系数随注液范围的变化规律

Fig. 12  Change law of minimum safety factor of slope with range of liquid injection

为验证模型计算结果的有效性，现根据现场实测数据，建立坡度为25°的矿山模型进行数值计算。为简化计算，在数值建模时进行如下简化，模型网格划分图如图13所示，图中蓝色线代表注液范围。

1) 采用试验矿区所在地屏南县的年均降雨量对模型进行初始入渗计算，以此得到天然状态下的矿山模型；

2) 与理论模型一致，即假定矿层是均质、各向同性的，即矿层不同深度处的抗剪强度参数相同；

3) 将现实生产原地浸矿的注液井注液方式简化为从矿层均匀向下入渗，对应的均匀入渗强度为0.43m/d。

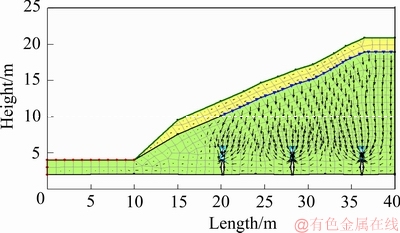
图13  边坡模型网格划分图

Fig. 13  Grid partition map of slope model

首先，先进行渗流计算，如图14所示。由图14可知，在有巷道工程收液的情况下，矿体内部溶液的渗流方向基本竖直向下，说明理论模型计算时假设未注液区域不受注液区域影响是合理的。

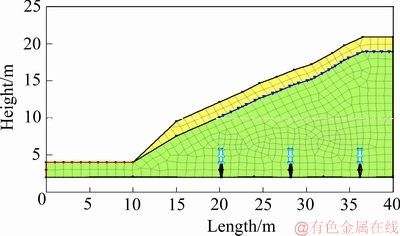
图14  边坡模型渗流计算图

Fig. 14  Seepage calculation diagram of slope model

完成渗流计算后，进行边坡安全系数的计算，确定潜在滑移面，如图15所示。经过计算可知，当注液范围约为22.70 m时，最小边坡安全系数为1.02，边坡处于临界安全状态，则该注液范围即为临界注液范围，本文理论模型所计算临界注液范围为26.28 m，两者的相对误差值为15.77%。故对于坡度为25°的边坡，本文理论模型可较好的预测出稀土矿山的临界注液 面积。

同理，可得到水平距离为30 m，坡度分别为30°和35°时临界注液范围的理论模型计算值和数值模型计算值，如表2所列。由表2可知，对于坡度为25°、30°和35°的边坡模型，临界注液范围理论计算值与数值计算值的相对误差值在20%以内，相对误差较小，说明了本文临界注液范围理论计算模型的有效性。

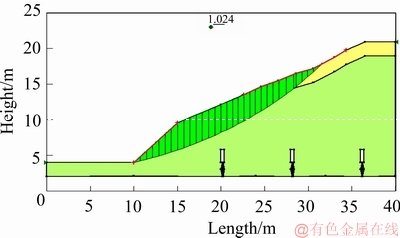
图15  边坡模型滑坡计算图

Fig. 15  Landslide calculation diagram of slope model

表2  临界注液范围的理论模型与数值模型计算值

Table 2  Theoretical model and numerical model calculation value of critical liquid injection range

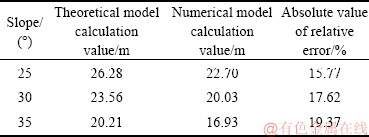
由表2可知，3种坡度下临界注液范围理论模型计算值大于数值计算值，主要原因：根据图14可知，在进行渗流计算时，溶液的渗流方向主要为竖向渗流，但注液区域与未注液区域交界区，部分溶液渗流进未注液区域，对未注液区域矿体的强度造成弱化，而在进行理论模型计算时，假定了未注液区域不受注液区域的影响，从而导致理论模型计算时矿体黏聚力取值偏大，造成理论模型计算值大于数值模型计算值。

同时，由表2可知，随着坡度的增大，临界注液范围理论模型计算值与数值计算值的误差逐渐增大，主要原因：随着坡度的增大，注液区域的溶液入渗到未注液区域逐渐增多，对未注液区域的影响逐渐增大，导致未注液区域矿体黏聚力进一步减小，使得采用理论模型计算得到的数值更加偏离实际值，从而导致临界注液范围理论模型计算值与数值计算值的误差进一步增大。

2.3.2  基于现场位移监测结果的模型有效性分析

在稀土矿山选定一测线，确定参考点，采用RTK测试地形；同时采用洛阳铲通过人工打孔的方式，由山顶至山脚，每隔5~10 m钻取一个孔，确定该测线表土平均厚度为3 m左右。根据现场实测结果，以山脊线为起点，地形主要分为3段：第1段坡度为8.37°，坡面距离为29.87 m；第2段坡度为31.91°，坡面距离为23.25 m；第3段坡度为42.17°，坡面距离为7.44 m。同时，现场注液范围为29.87 m，即为第一段缓坡区域，注液范围百分比为49.32%。

为监测山体变形情况，将距离山脊线10 m左右位置处作为起点，第一段缓坡区域布置一个位移计，跨度20 m，命名为1号位移计；第二段和第三段陡坡区域布置两个位移计，跨度15m，分别命名为2号和3号位移计。从注液开始即监测山体的边坡变形情况，如图16所示。由图16可知，随着注液时间的增加，缓坡区域处于拉伸状态，在注液的第87 d边坡位移达到4.5 mm；陡坡区域上部处于拉伸状态，在注液的第87 d边坡位移达到24.4 mm；陡坡区域下部处于压缩状态，在注液的第87 d边坡位移达到-2.4 mm。故随时间推移，边坡中前部位移不断增大，其产生的推力不断向边坡后部传递，造成边坡后部的压缩，边坡可能发生滑裂口位于后部的整体式滑移，由这种滑移方式形成的滑坡称为推移式滑坡^[11]。

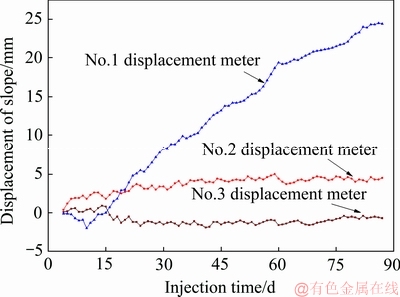
图16  边坡位移随注液时间的变化规律

Fig. 16  Change law of displacement of slope with injection time

由此，可采用上述所建理论模型进行该边坡临界注液面积的计算。根据前文所述计算原理，对于注液区域，坡体表面与水平面的夹角β₁=8.37°；试验矿区表土平均厚度在3 m左右，转化为均布压力q=61.80 kPa；其余参数取值与前文相同，求得不同见矿深度下的下滑力P_a。对于未注液区域，取L_AD=30.59 m；坡脚β₂=34.38°；表土平均厚度在3m左右，转化为均布压力q=61.80 kPa；其余参数取值与前文相同，求得不同见矿深度下抗滑力T_s。

根据求取的不同见矿深度下的抗滑力与下滑力，求得边坡安全系数随见矿深度的变化规律，如图17所示。由图17可知，随着见矿深度的增加，边坡安全系数先减小后增大，当见矿深度为6.5 m时，边坡安全系数达到最小值2.40，则边坡是稳定的。根据文献[18]可知，对于类均质边坡，当最小边坡安全系数为2.216时，边坡上部发生拉伸变形，下部发生压缩变形，且边坡上部位移明显大于边坡下部。该文献中的安全系数与理论模型计算值接近，边坡位移变化规律与现场边坡位移监测结果吻合，进一步说明了理论计算模型的有效性。

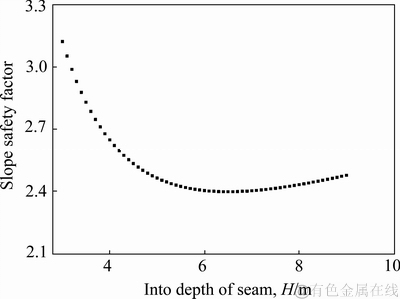
图17  边坡安全系数随见矿深度的变化规律

Fig. 17  Change law of slope safety factor with depth of entering seam

2.3.3  临界注液范围计算模型的优越性分析

本文所建理论模型通过与数值计算和现场位移监测结果的对比说明了模型的有效性，现与传统的滑坡分析方法作对比，说明其优越性。传统的滑坡分析方法主要包括极限平衡法和数值分析法(有限元法)，但这两种方法运用于离子型稀土矿山临界注液范围的计算均存在一定的缺陷，在本文引言中已作介绍，现阐述本文所建理论模型的优越性。

相对于极限平衡法，本文所建理论模型在进行下滑力和抗滑力的计算时，无需进行土条的划分，同时根据模型计算结果显示，随着见矿深度的增加，边坡安全系数先减小后增大，由此确定了最小安全系数所对应的见矿深度，从而确定了最危险滑移面，克服了极限平衡法中需假定滑移面进行不断试算和计算结果受所划分土条宽度影响的缺陷。同时，在进行下滑力和抗滑力的计算时，可采用现有研究中的分层总和法进行计算，由此考虑矿体非均质的情况，克服了极限平衡法中无法考虑矿体非均质的缺陷。

相对于数值分析法，理论模型中仅涉及到的矿体参数主要为原位矿体的重度、矿体的含水率分布及其抗剪强度参数，在现有技术条件下，这些参数获取难度不大，这在文中已有相关介绍，同时该模型可进一步考虑浸矿作用对这些参数的影响，从而更精确计算离子型稀土矿山的临界注液范围，避免了由离子型稀土矿山收液工程具体布置方式和深层原位矿体的土水特征曲线及渗透系数等部分物理力学参数值的选取对计算结果的影响。

3  结论

1) 对于全覆式离子型稀土矿山，其边坡的滑坡类型以推移式滑坡为主，通过注液边界将潜在滑坡体分为两部分，注液区潜在滑坡体提供下滑力，未注液区潜在滑坡体提供抗滑力，在考虑浸矿液对矿体强度弱化作用的基础上，基于黏性土土压力的计算方法和简化Bishop法，建立了稳渗状态下矿山临界注液范围的计算模型，并通过对比3种坡度临界注液范围的理论模型计算值和数值模型计算值，说明了理论模型的有效性。

2) 矿体内摩擦角随着体积含水率的增大基本保持不变，矿体黏聚力的对数与其体积含水率呈线性关系。

3) 浸矿周期随着矿体体积含水率的增大先减小后趋于稳定，矿体的浸取率与其体积含水率呈负指数函数关系。

4) 对于坡度为25°、30°或35°的简单边坡，临界注液范围理论计算值与数值计算值的相对误差绝对值在20%以内，相对误差较小，说明本文临界注液范围理论计算模型的有效性。

REFERENCES

[1] 吴爱祥, 尹升华, 李建锋. 离子型稀土矿原地溶浸溶浸液渗流规律的影响因素[J]. 中南大学学报(自然科学版), 2005, 36(3): 506-510.

Wu Ai-xiang, Yin Sheng-hua, Li Jian-feng. Influential factors of permeability rule of leaching solution in ion-absorbed rare earth deposits with in-situ leaching[J]. Journal of Central South University (Science and Technology), 2005, 36(3): 506-510.

[2] 饶 睿, 李明才, 张树标, 饶运章, 钟健民. 离子型稀土原地浸矿采场滑坡特征及防控试验研究[J]. 稀土, 2016, 37(6): 26-31.

RAO Rui, LI Ming-cai, ZHANG Shu-biao, RAO Yun-zhang, ZHONG Jian-min. Experimental study on landslide features and countermeasures of in situ leaching stope of ion type rare earth mines[J]. Chinese Rare Earths, 2016, 37(6): 26-31.

[3] PINK M N. Analysis of slope stability by the method of limiting equilibrium[J]. Soil Mechanics and Foundation Engineering, 2007, 44(3): 99-104.

[4] YU Zhi-fa, LI Bin, HUANG Chuan-zhi. Research on limit equilibrium method of three-dimensional slope stability[J]. Archive of Applied Mechanics, 2018, 88(7): 1175-1186.

[5] PASTERNACK S C, GAO S. Numerical methods in the stability analysis of slopes[J]. Computers and Structures, 1988, 30(3): 573-579.

[6] SHEN J Y, KARAKUS M. Three-dimensional numerical analysis for rock slope stability using shear strength reduction method[J]. Canadian Geotechnical Journal, 2014, 51(2): 164-172.

[7] 蔡征龙, 孟永东, 苏情明, 朱伟玺. 基于Matlab的土坡稳定分析的解析计算[J]. 三峡大学学报(自然科学版), 2014, 36(5): 60-63.

CAI Zheng-long, MENG Yong-dong, SU Qing-ming, ZHU Wei-xi. Analytical calculation of soil slope stability based on Matlab[J]. J of China Three Gorges Univ (Natural Sciences), 2014, 36(5): 60-63.

[8] KUMAR N, VERMA A K, SARDANA S, SARKAR K, SINGH T N. Comparative analysis of limit equilibrium and numerical methods for prediction of a landslide[J]. Bulletin of Engineering Geology and the Environment, 2018, 77(2): 595-608

[9] 郑颖人. 岩土数值极限分析方法的发展与应用[J].岩石力学与工程学报, 2012, 31(7): 1297-1316.

ZHENG Ying-ren. Development and application of numerical limit analysis for geological materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1297-1316.

[10] 桂 勇, 王观石, 赖远明, 洪本根, 胡世丽, 龙 平. 原地浸矿单孔注液影响半径的计算模型[J]. 中国有色金属学报, 2018, 28(5): 1050-1058.

GUI Yong, WANGGuan-shi, LAIYuan-ming, HONG Ben-gen, HU Shi-li, LONG Ping. A calculation model of influence radius of single-hole injection in in-situ leaching[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(5): 1050-1058.

[11] 雍 睿, 胡新丽, 唐辉明, 李长冬, 马俊伟, 宋友建. 推移式滑坡演化过程模型试验与数值模拟研究[J]. 岩土力学, 2013, 34(10): 3018-3027.

YONG Rui, HU Xin-li, TANG Hui-ming, LI Chang-dong, MA Jun-wei, SONG You-jian. Model testing and numerical simulation study of evolutionary process of thrust load caused landslide[J]. Rock and Soil Mechanics, 2013, 34(10): 3018-3027.

[12] 顾慰慈. 挡土墙土压力计算手册[M]. 北京: 中国建材工业出版社, 2005.

GU Wei-ci. Handbook for earth preasure calculation of retaining wall[M]. Beijing: China Building Materials Industry Press, 2005.

[13] 张鲁渝, 郑颖人. 简化Bishop法的扩展及其在非圆弧滑面中的应用[J]. 岩土力学, 2004, 25(6): 927-929, 934.

ZHANG Lu-yu, ZHENG Ying-ren. An extension of simplified Bishop method and its application to non-circular slip surface for slope stability analysis[J]. Rock and Soil Mechanics, 2004, 25(6): 927-929, 934.

[14] DENG Dong-ping, ZHAO Lian-heng, LI Liang. Limit equilibrium stability analysis of slopes under external loads[J]. Journal of Central South University, 2016, 23(9): 2382-2396.

[15] 袁志辉, 倪万魁, 刘 茹, 李焕焕. 基于吸应力的非饱和黄土抗剪强度研究[J]. 合肥工业大学学报(自然科学版), 2015, 38(5): 648-653.

YUAN Zhi-hui, NI Wan-kui, LIU Ru, LI Huan-huan. Study of shear strength of unsaturated and undisturbed loess based on suction stress[J]. Journal of Heifei University of Technology, 2015, 38(5): 648-653.

[16] 林鸿州, 李广信, 于玉贞, 吕 禾. 基质吸力对非饱和土抗剪强度的影响[J]. 岩土力学, 2007, 28(9): 1931-1936.

LIN Hong-zhou, LI Guang-xin, YU Yu-zhen, Lü He. Influence of matric suction on shear strength behavior of unsaturated soils[J]. Rock and Soil Mechanics, 2007, 28(9): 1931-1936.

[17] 于斯滢, 邵龙潭, 刘士乙. 基于有限元极限平衡法的尾矿坝坝体稳定分析[J]. 岩土力学, 2013, 34(4): 1185-1190.

YU Si-ying, SHAO Long-tan, LIU Shi-yi. Stability analysis of tailings dam based on finite element limit equilibrium method[J]. Rock and Soil Mechanics, 2013, 34(4): 1185-1190.

[18] 唐晓松, 郑颖人, 唐辉明. 边坡变形破坏演化特征的数值分析[J]. 重庆大学学报, 2013, 36(10): 101-113.

TANG Xiao-song, ZHENG Ying-ren, TANG Hui-ming. Numerical analysis on the evolutionary features of deformation and failure modes of slopes[J]. Journal of Chongqing University, 2013, 36(10): 101-113.

Calculation of critical liquid injection range in full clad ion-absorbed rare earth mine

HONG Ben-gen¹, LUO Si-hai², HU Shi-li², WANG Guan-shi²

(1. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;

2. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)

Abstract: For completely covered ionic-type rare earth mine, it is of great significance to master the calculation method of critical liquid injection range for determining the reasonable liquid injection range. The potential landslide mass was divided into two parts by liquid injection boundary, the potential landslide mass in liquid injection area provides glide force, the potential landslide mass in uninjected liquid area provides anti-sliding force. Based on the earth pressure calculation method of cohesive soil and simplified Bishop method, the theoretical model of critical liquid injection range under steady seepage condition was established. The validity of the theoretical model was verified by numerical results and field displacement monitoring results. The results show that, first，for a simple slope with a slope of 25°, 30° or 35°, the absolute relative error between theoretical model calculation value and numerical model calculation value of critical liquid injection range is less than 20%, the absolute relative error is smaller, the validity of the theoretical calculation model of critical liquid injection range is  preliminary explained. Second，for a field slope, the slope safety factor calculated by the theoretical model coincides with the variation of slope displacement, the validity of the theoretical calculation model of critical liquid injection range is explained again.

Key words: ionic-type rare earth mine; glide force; anti-sliding force; slope safety factor; critical liquid injection range

Foundation item: Projects(41602311, 51664015) supported by the National Natural Science Foundation of China; Project(YB2017003) supported by Jiangxi University of Science and Technology Excellent Doctoral Dissertation Nurturing Project, China

Received date: 2018-06-22; Accepted date: 2019-03-26

Corresponding author: HU Shi-li; Tel: +86-13576686778; E-mail: hslqhd@ 163.com

(编辑  王  超)

基金项目：国家自然科学基金资助项目(41602311，51664015)；江西理工大学优秀博士学位论文培育项目(YB2017003)

收稿日期：2018-06-22；修订日期：2019-03-26

通信作者：胡世丽，副教授，博士；电话：13576686778；E-mail：hslqhd@163.com